Similar presentations:
Розв’язування тригонометричних рівнянь
1. Математика
Навчальна презентація до уроку“Розв’язування тригонометричних
рівнянь”
2. Тригонометричні рівняння
Практикум по розв’язуванню таскладанню тригонометричних
рівнянь
3. Мета уроку:
Повторити основні формули іметоди розв’язування
тригонометричних рівнянь ;
Закріпити уміння і навики
розв’язування тригонометричних
рівнянь;
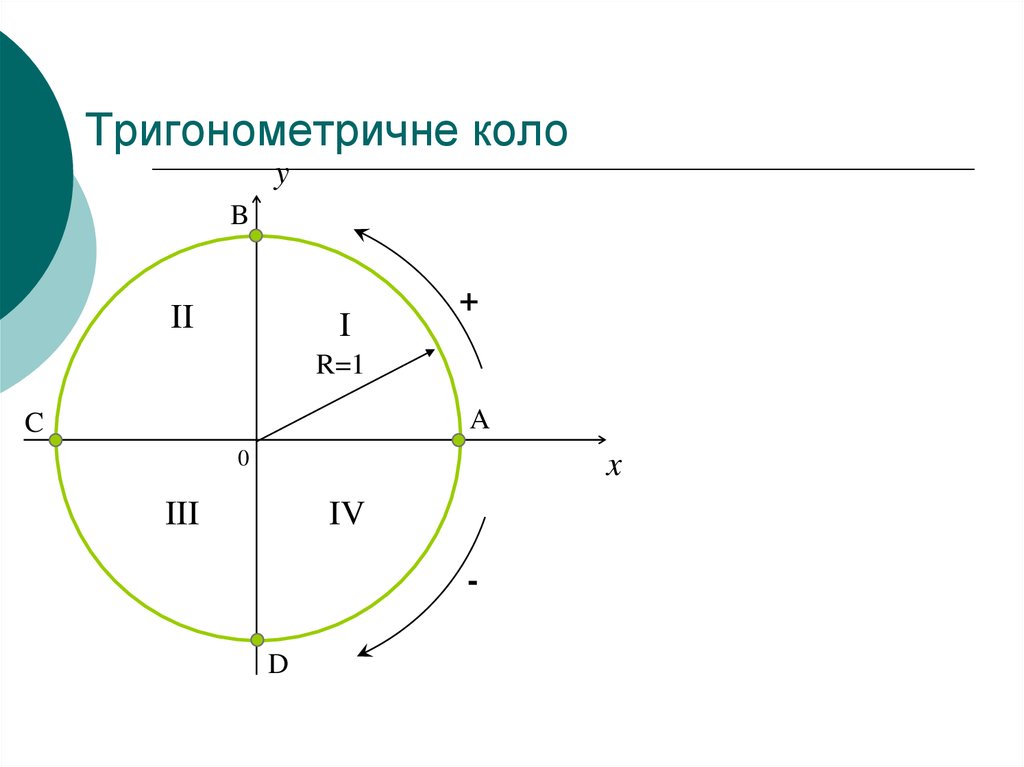
4. Тригонометричне коло
yB
II
I
+
R=1
A
C
0
x
III
IV
D
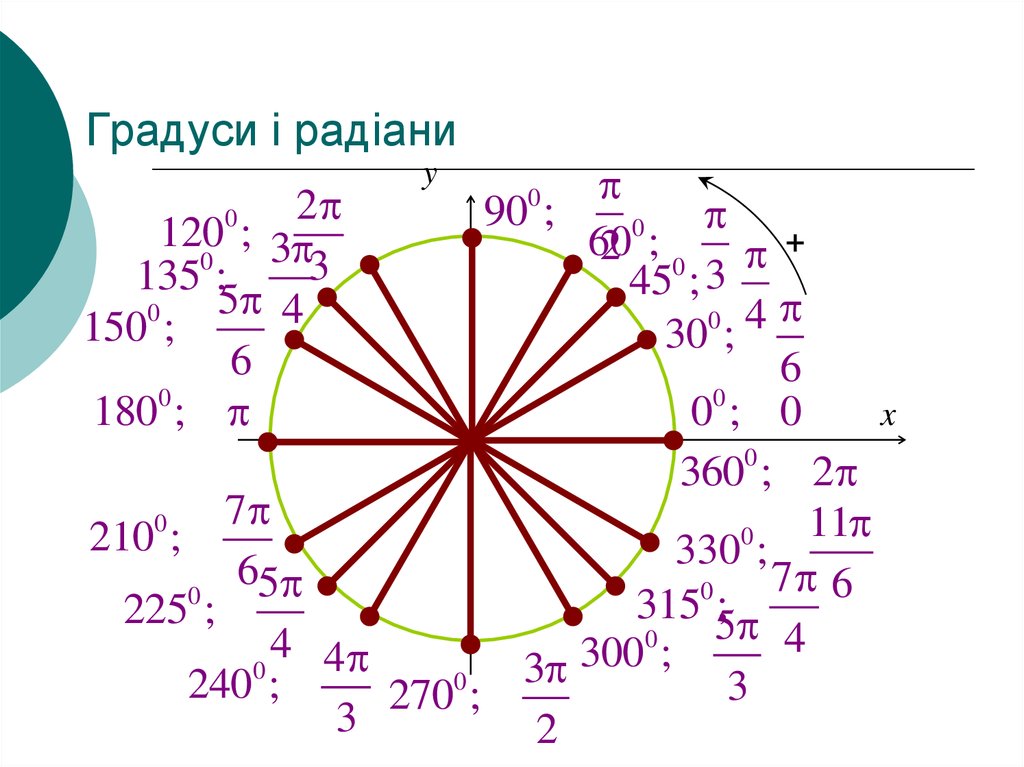
5. Градуси і радіани
290
;
0
0
120 ; 3
60
;0 +
2
0
3
3
135 ;
45
;
5 4
0
0 4
150 ;
30 ;
6
6
x
00 ; 0
1800 ;
0
0
360 ; 2
7
0
11
0
210 ;
330
;
6
7 6
5
0
0
315 5;
225 ;
0
4
4
300
;
4
3
0
2400 ;
3
270 ;
3
2
y
0
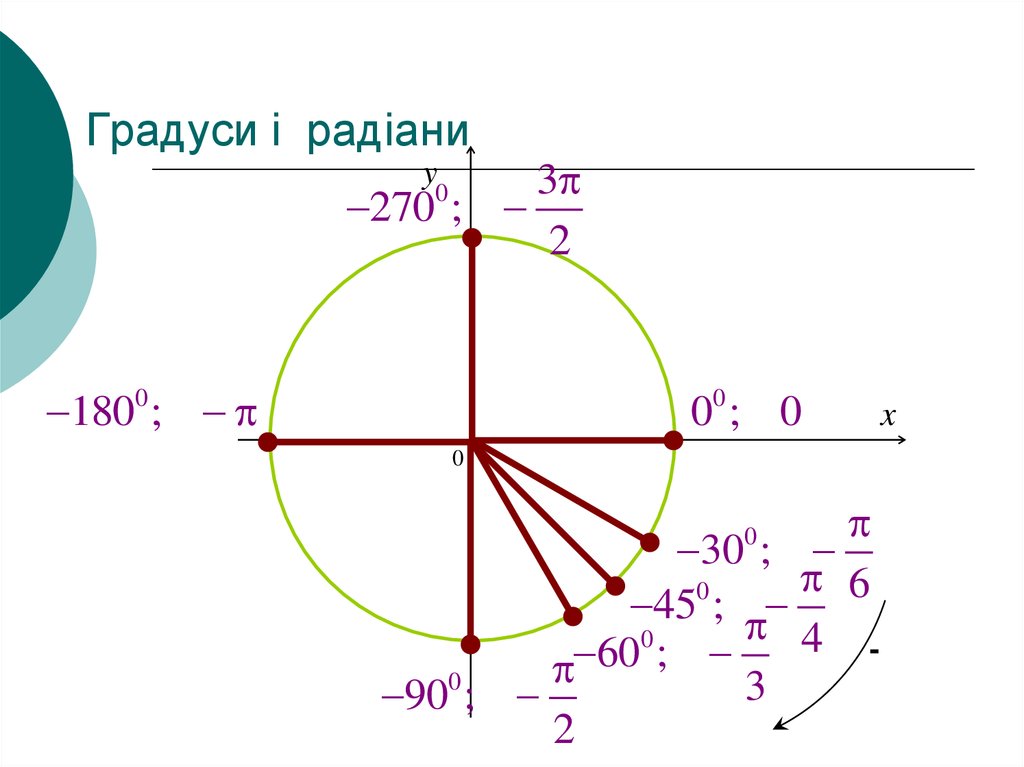
6. Градуси і радіани
3270 ;
2
y
0
1800 ;
00 ; 0
x
0
30 ;
6
0
45 ;
0
4
60
;
0
3
90 ;
2
0
-
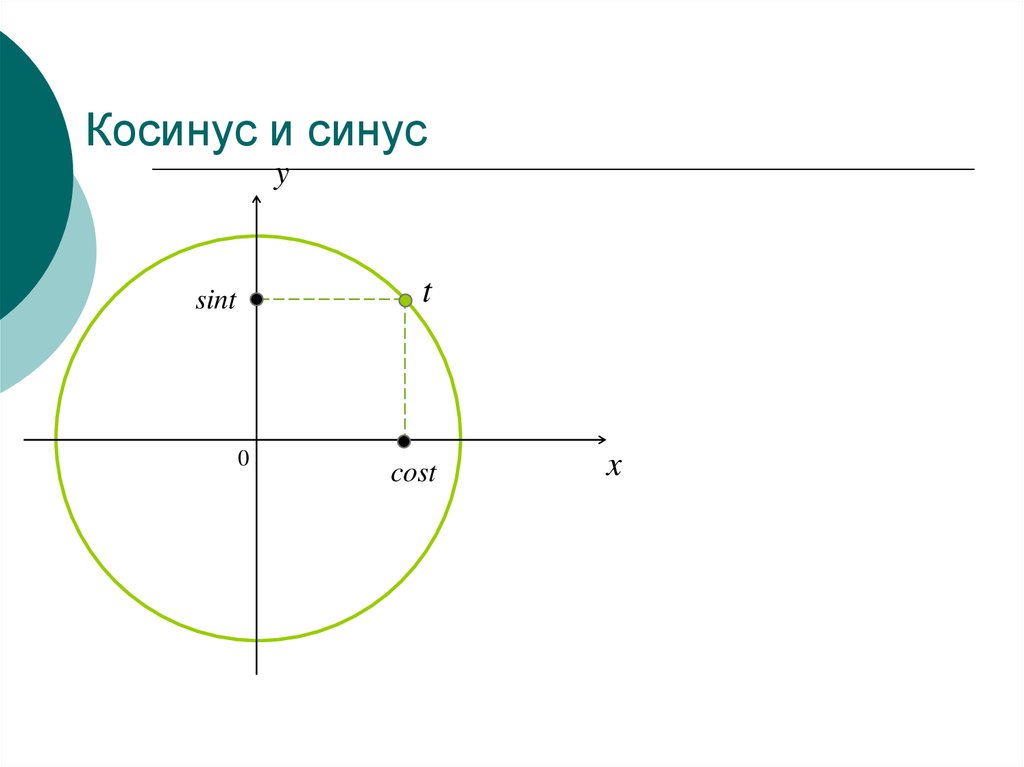
7. Косинус и синус
yt
sint
0
cost
x
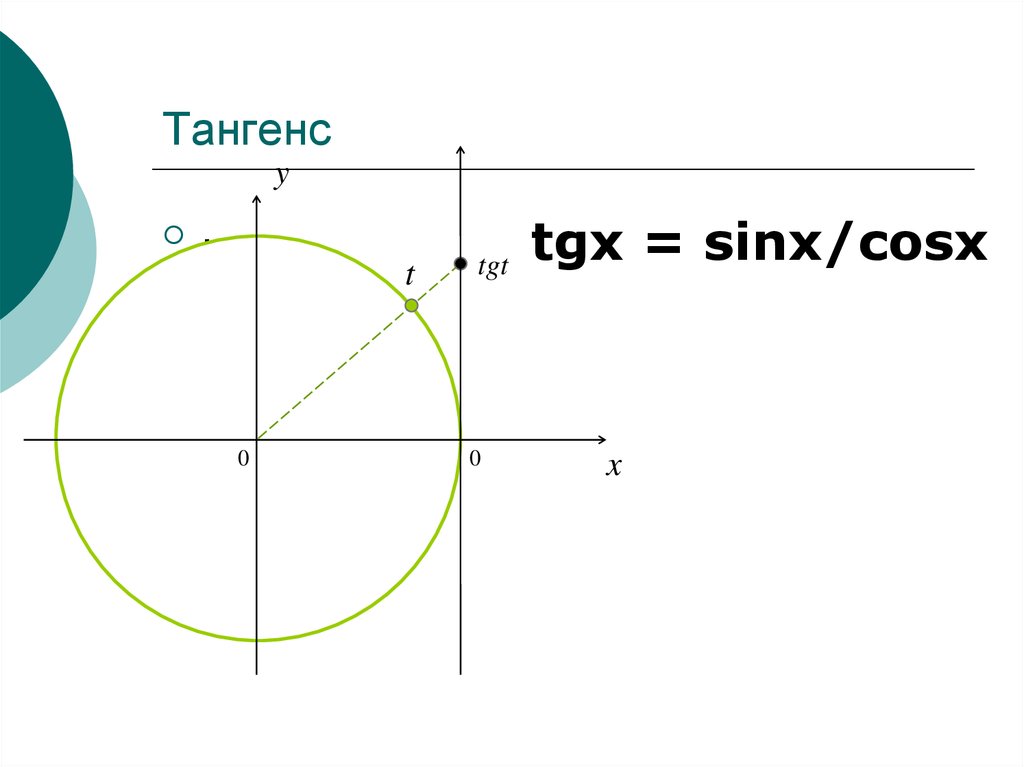
8. Тангенс
y.
t
0
tgt
0
tgx = sinx/cosx
x
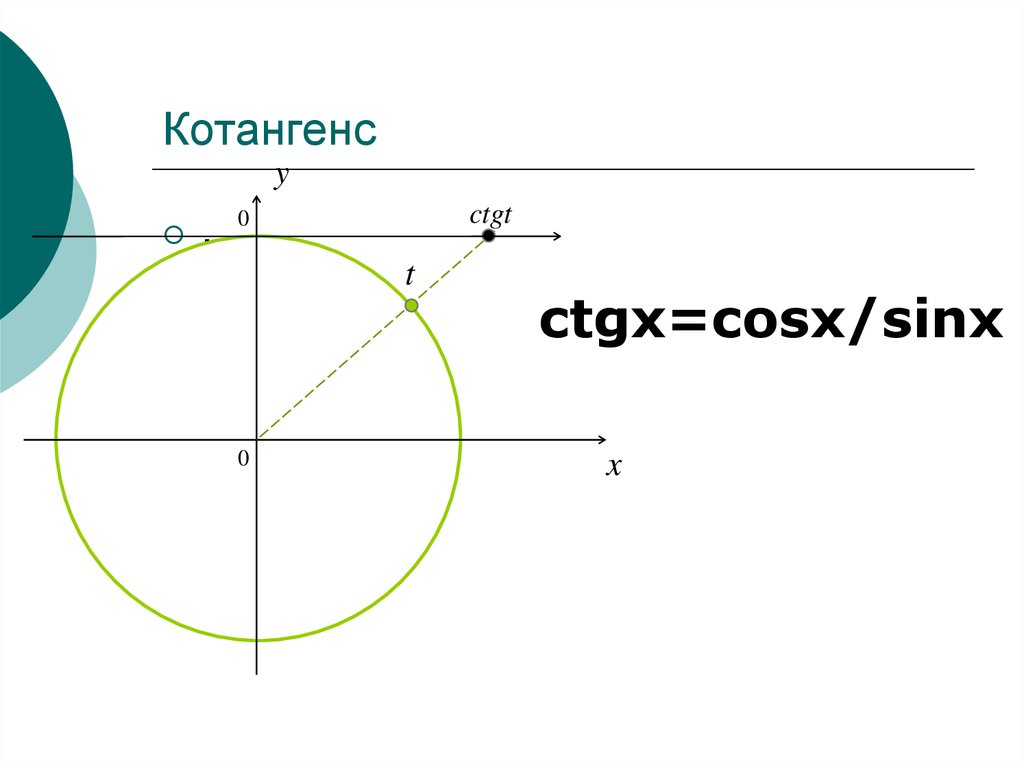
9. Котангенс
y.
ctgt
0
t
0
ctgx=cosx/sinx
x
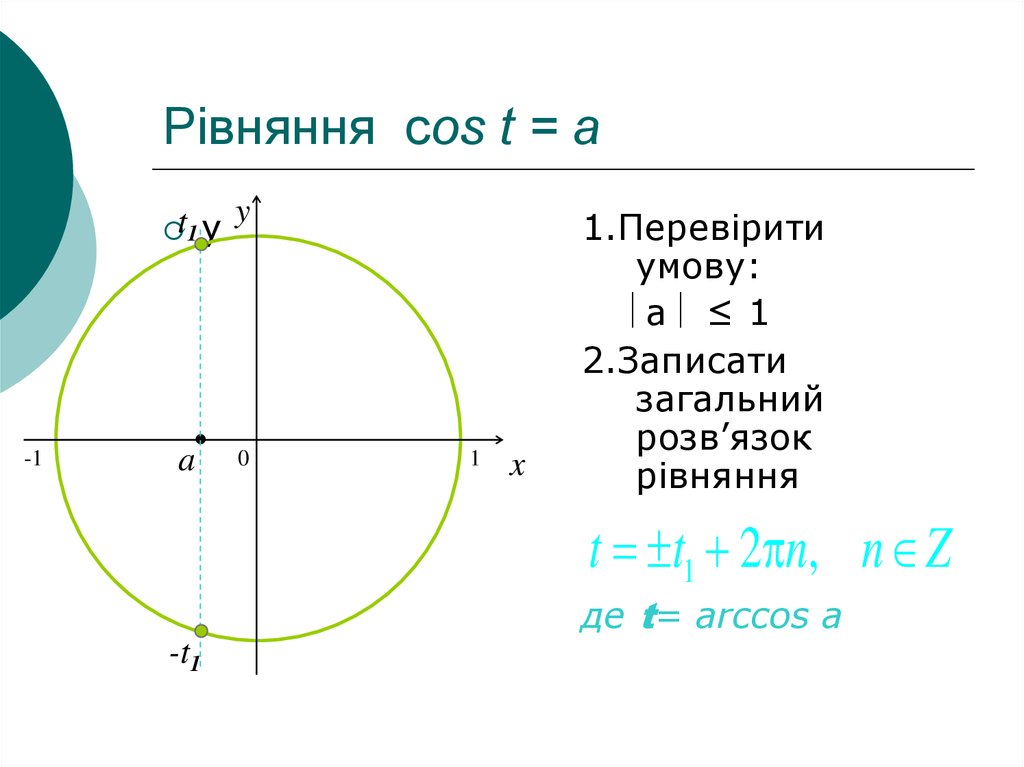
10. Рівняння сos t = a
-1t1 у
y
a
0
1
x
1.Перевірити
умову:
a ≤ 1
2.Записати
загальний
розв’язок
рівняння
t t1 2 n, n Z
де t= arccos a
-t1
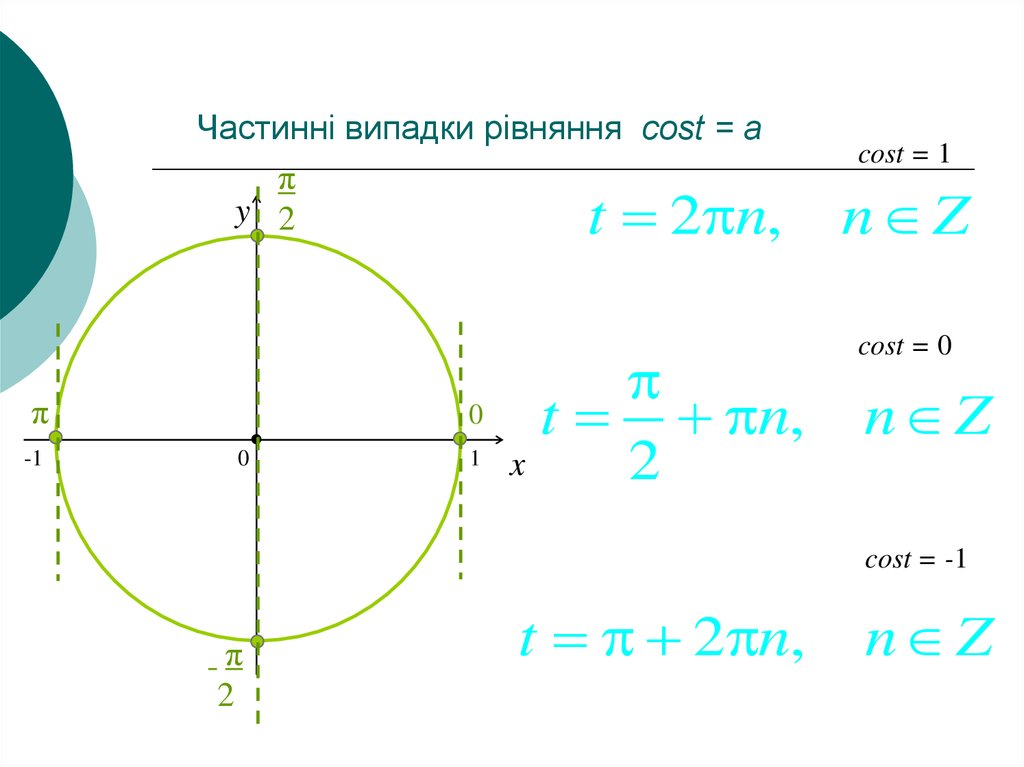
11. Частинні випадки рівняння cost = a
πy 2
t 2 n,
π
-1
0
0
1
t n,
x
2
cost = 1
n Z
cost = 0
n Z
cost = -1
π
2
t 2 n,
n Z
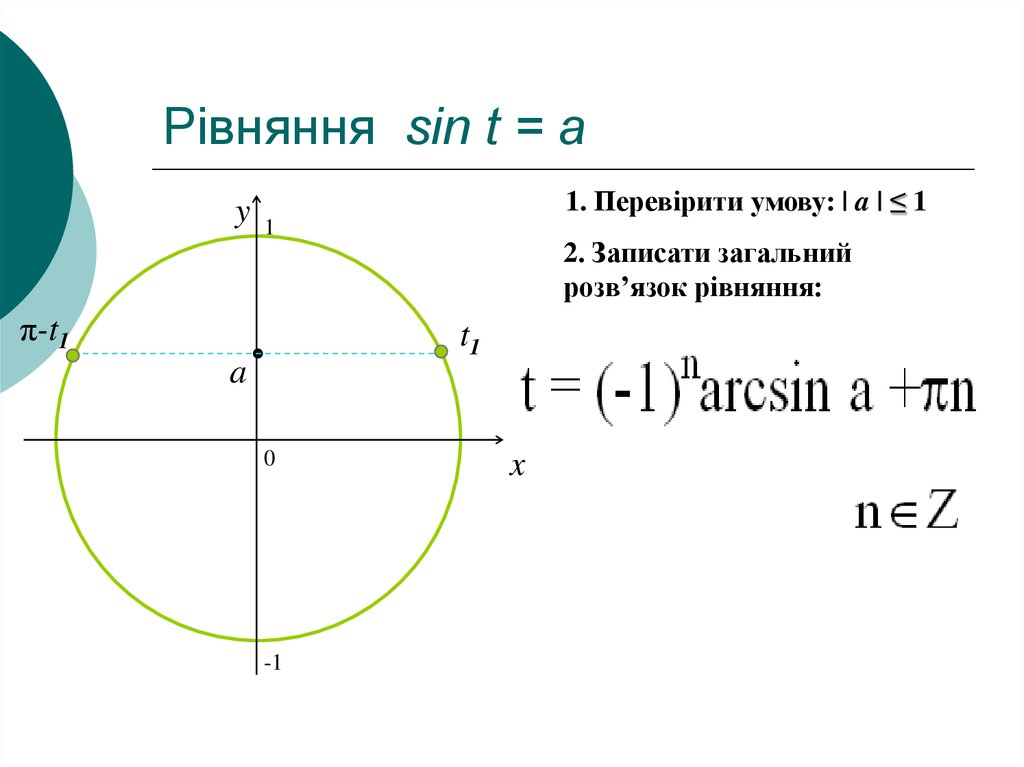
12. Рівняння sin t = a
y1. Перевірити умову: | a | ≤ 1
1
π-t1
2. Записати загальний
розв’язок рівняння:
t1
a
0
-1
x
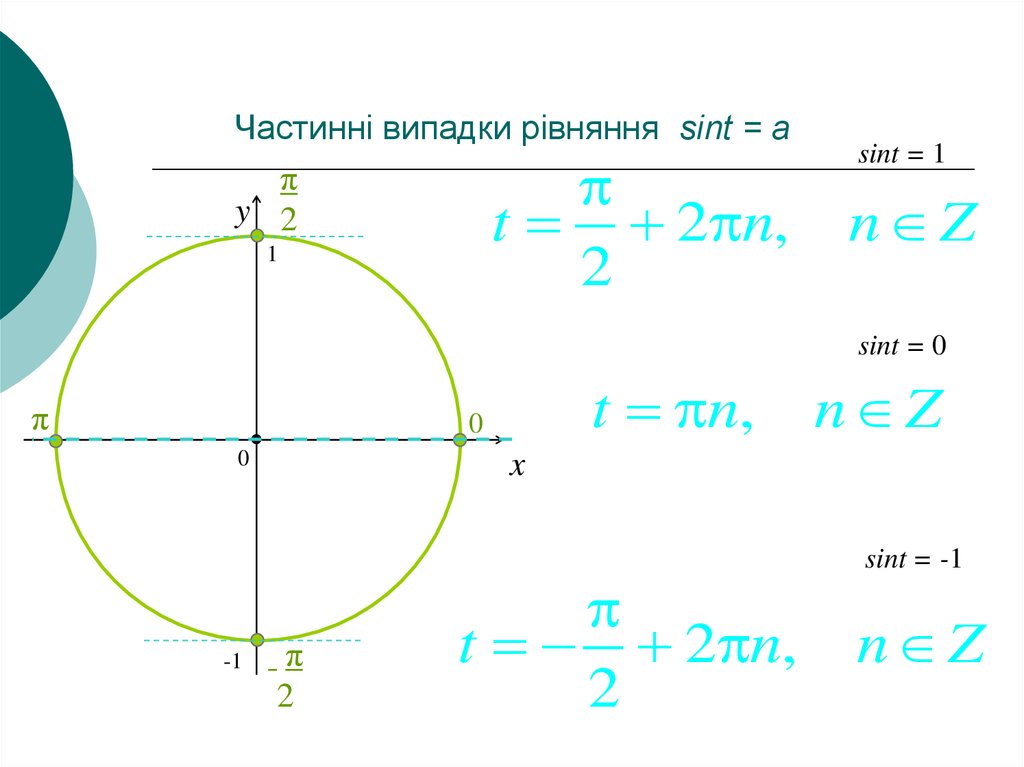
13. Частинні випадки рівняння sint = a
πy 2
t 2 n,
2
1
sint = 1
n Z
sint = 0
π
t n,
0
0
-1
n Z
x
π
2
t 2 n,
2
sint = -1
n Z
14. Приклади розв’язування тригонометричних рівнянь й
Приклад 1.15.
Приклад 2.16.
Приклад 3.sin 2x + sin x= 0
sin 2x = 2 sin x cos x
2 sin x cos x + sin x = 0
sin x (2 cos x + 1) = 0
17.
Приклад 4.4 tg x – 3 ctg x = 1
ctg x = 1/ tg x








 mathematics
mathematics








