Розв’язування найпростіших тригонометричних рівнянь

1.

Розв’язування
найпростіших
тригонометричних
рівнянь.

2.

Обчисліть і запишіть в зошит
результати:
1
3
1.arcsin
5.arcsin (– )
2
2
2. arccos
2
2
3. arctg 3
4. arctg (
Звірте
відповіді:
3
-3
6. arccos (-1)
3
2
7. arcсоs(
)
)

3.

До найпростіших тригонометричних рівнянь
належать рівняння виду:
sin x a
cos x a
tgx a
ctgx a

4.

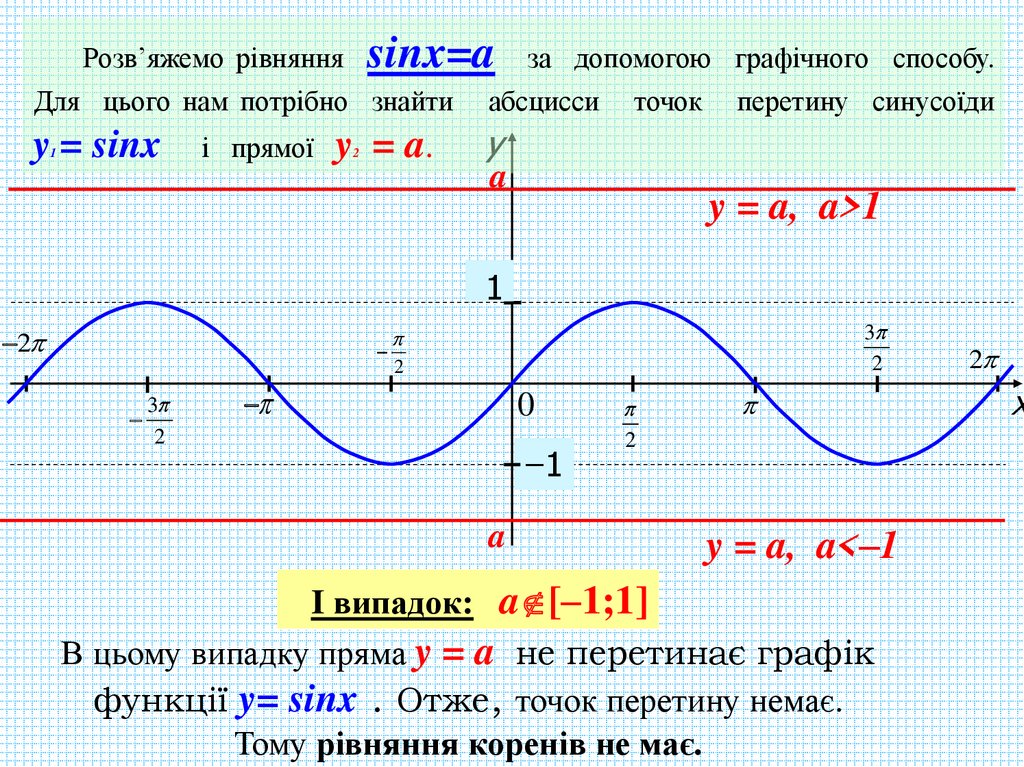
sinx=a
Розв’яжемо рівняння
за допомогою графічного способу.
Для цього нам потрібно знайти
абсцисси
y = sinx
y
1
і прямої
y = a.
2
точок
a
перетину синусоїди
y = a, a>1
1
2
3
2
3
2
2
0
−1
a
2
y = a, a<–1
I випадок: a [–1;1]
В цьому випадку пряма y = a не перетинає графік
функції y= sinx . Отже, точок перетину немає.
Тому рівняння коренів не має.
2
x

5.

II випадок: a [–1;1]
Очевидно, що в цьому випадку точок перетину безліч,
причому їх абсцисси визначаються наступним чином:
1) Розглянемо точку, абсциса якої належить проміжку 2 ; 2
2) Абсциса цієї точки – це число(кут), синус якого дорівнює
a,
.
тобто значення цього числа дорівнює arcsina.
2
3
2
arcsin a arcsin a
2
2
1
a
y
3
2
2
0
arcsin a arcsin a
2
x
2
−1
3) Абсциса другої точки належить відрізку [– ; ] і дорівнює
( –arcsina). Щоб це пояснити достатньо пригадати, що sinx = sin( –x).
4) Всі інші абсцисси точок перетину отримуємо враховуючи
періодичність функції y = sinx (Т=2 n, де n Z).
Завдання: назвіть абсциси двох
Відповідь: (arcsina+2π) і
наступних точок перетину справа.
(3π – arcsina).

6.

2
Отже, всі корені в цьому випадку можна записати у вигляді
сукупності:
sin x a
arcsin a ·2n, n Z;;
x
arcsin a · 2k 1 , k Z/.
y
1
3
2
arcsin a arcsin a
2
2
3
2
a
2
0
arcsin a arcsin a
2
−1
Або, ці два записи об’єднують в одну формулу
(подумайте, як це пояснити):
x 1 arcsin a m, m Z..
m
2
x

7.

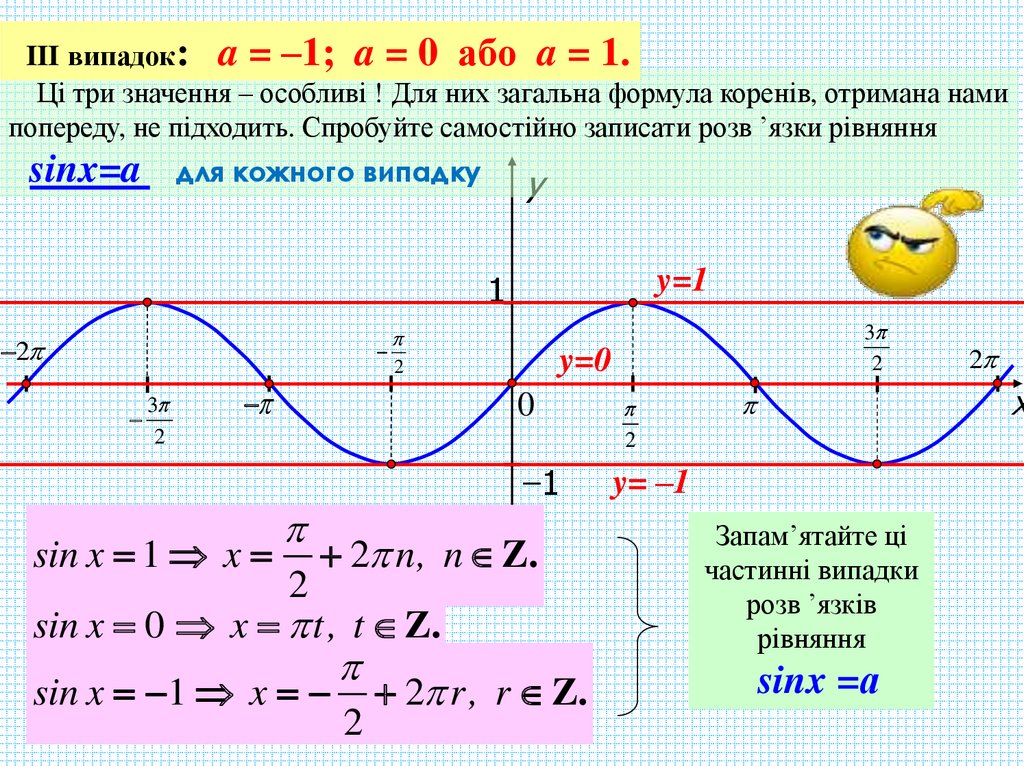
III випадок: a = –1; a = 0 або a = 1.
Ці три значення – особливі ! Для них загальна формула коренів, отримана нами
попереду, не підходить. Спробуйте самостійно записати розв ’язки рівняння
для кожного випадку
sinx=a
y
y=1
1
2
3
2
sin x 1 x
y=0
2
3
2
0
x
2
−1
2 n, n Z..
2
sin x 0 x t, t Z..
sin x 1 x
2
2 r, r Z..
2
y= –1
Запам’ятайте ці
частинні випадки
розв ’язків
рівняння
sinx =а

8.

Розв’яжемо рівняння cosx=a теж за допомогою графічного способу. Для
цього нам потрібно знайти абсцисси точок перетину косинусоїди
y = cosx
та прямої
y = a.
y
y=a, a>1
a
1
2
3
2
3
2
2
0
2
−1
a
y=a, a< –1
I випадок: a [–1;1]
Очевидно, що в цьому випадку точок перетину немає.
Тому рівняння коренів не має.
2
x

9.

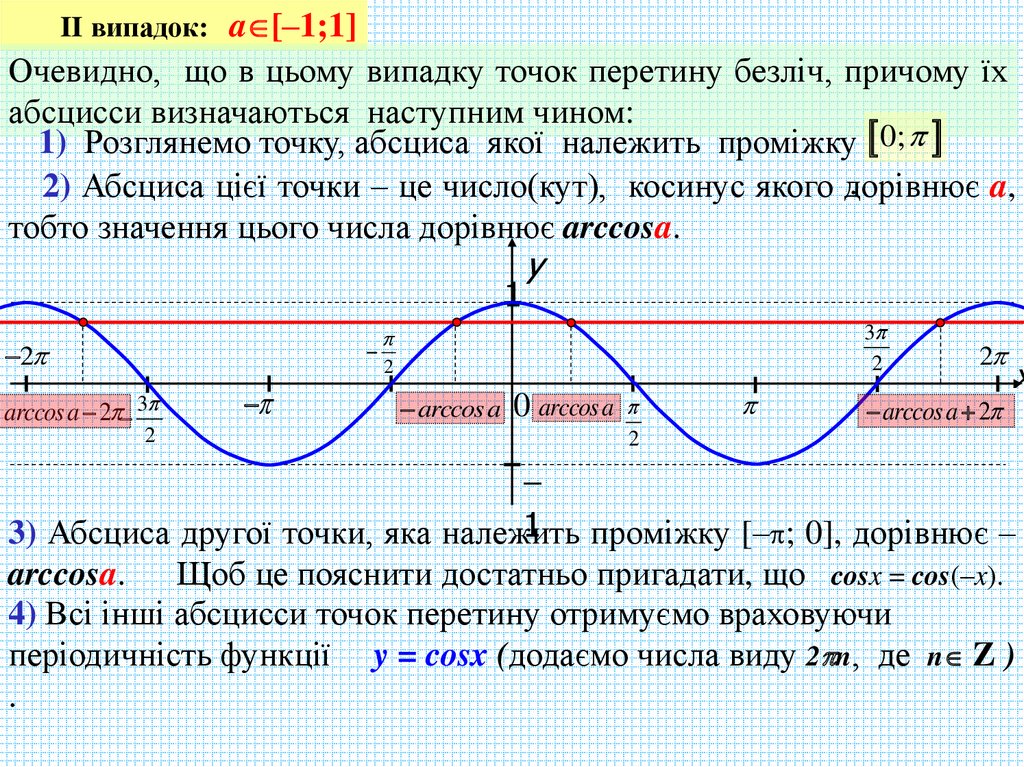
II випадок: a [–1;1]
Очевидно, що в цьому випадку точок перетину безліч, причому їх
абсцисси визначаються наступним чином:
1) Розглянемо точку, абсциса якої належить проміжку 0;
.
2) Абсциса цієї точки – це число(кут), косинус якого дорівнює
a,
тобто значення цього числа дорівнює arccosa.
1
2
arccos a 2 3
2
y
3
2
2
arccos a
0 arccos a
2
2
arccos a 2
x
−
1 проміжку [– ; 0], дорівнює –
3) Абсциса другої точки, яка належить
arccosa. Щоб це пояснити достатньо пригадати, що cosx = cos(–x).
4) Всі інші абсцисси точок перетину отримуємо враховуючи
періодичність функції y = cosx (додаємо числа виду 2 n, де n Z )
.

10.

Таким чином, всі корені в цьому випадку можна записати у вигляді
сукупності:
cos x a
arccos a 2 n, n Z;;
x
arccos a 2 k , k Z/.
1
2
arccos a 2 3
2
y
Масштаб :3
3
2
2
arccos a
0 arccos a
2
arccos a 2
−
1
Досить часто ці два записи об’єднують в один:
x arccos a 2 m, m Z/.
2
x

11.

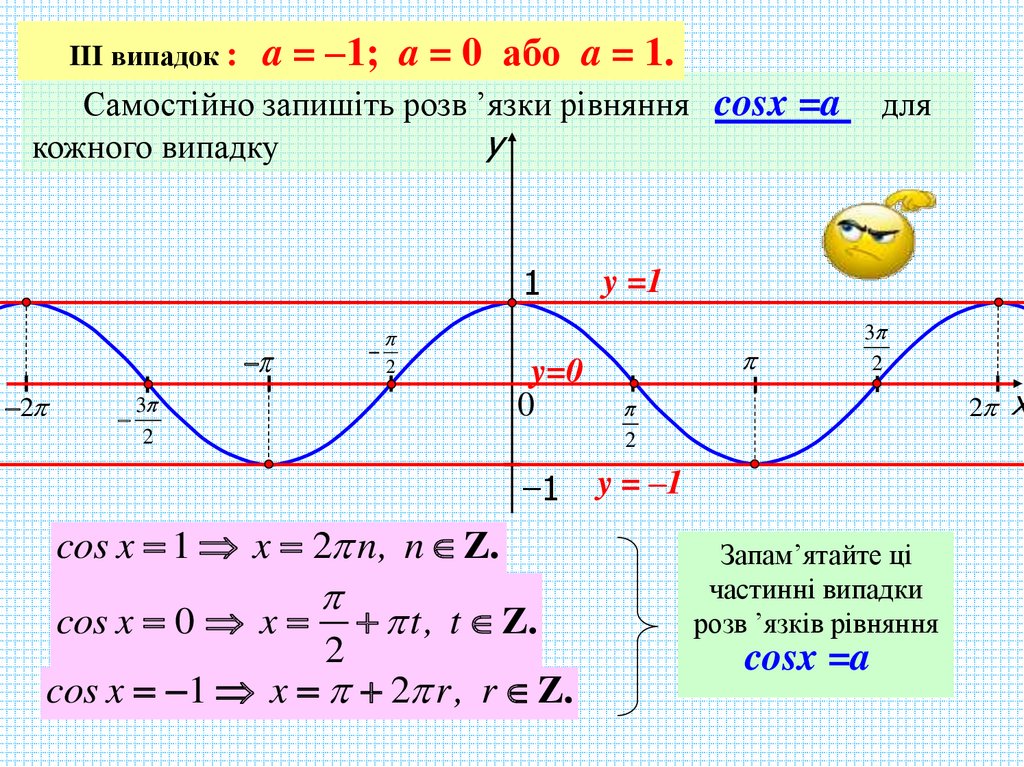
III випадок :
a = –1; a = 0 або a = 1.
Самостійно запишіть розв ’язки рівняння cosx =a
y
кожного випадку
1
2
3
2
y =1
2
y=0
0
для
3
2
2
2
−1
cos x 1 x 2 n, n Z..
cos x 0 x t, t Z..
2
cos x 1 x 2 r, r Z..
y = –1
Запам’ятайте ці
частинні випадки
розв ’язків рівняння
cosx =a
x

12.

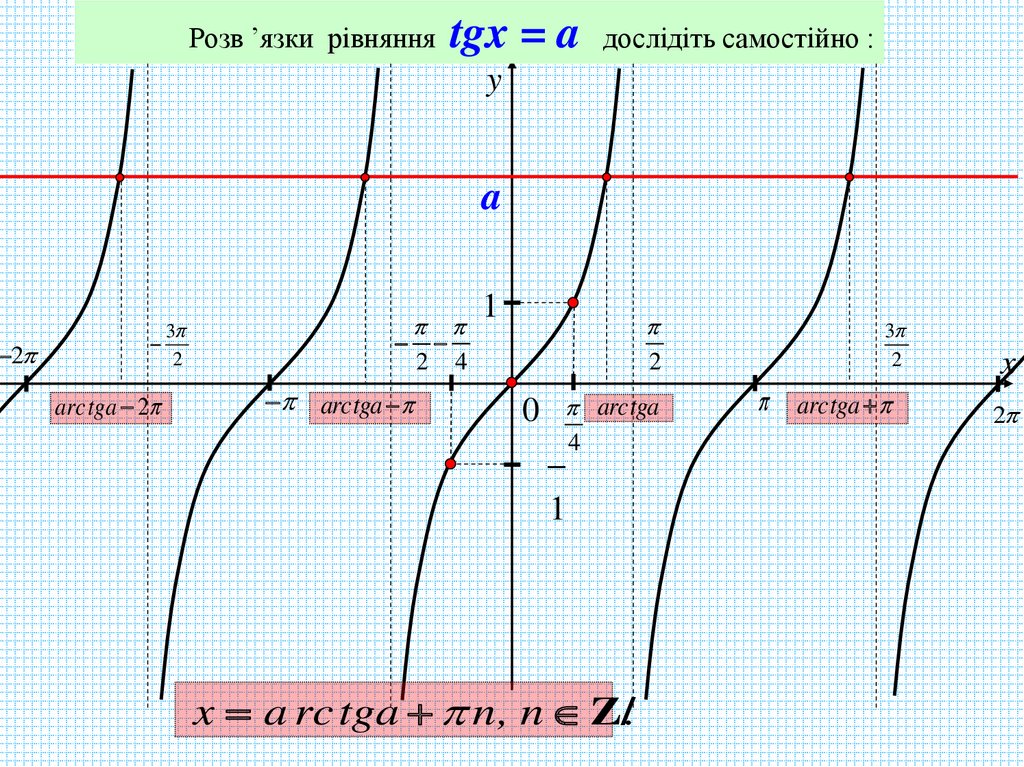
2
Розв ’язки рівняння
tgx = a
дослідіть самостійно :
y
a
arc tga 2
3
2
2 4
arctga
1
2
0
arctga
−
1
4
x a rc tga n, n Z/.
3
2
arctga
x
2

13.

Розв ’язки рівняння
сtgx = a
дослідіть самостійно :
y
a
2
arc ctga 2
3
2
arcctga
1
4
2
0
arcctga
2
3
4
3
2
arcctga
−
1
x a rc ctga n, n Z/.
x
2

14.

Розв’язання будь-яких тригонометричних рівнянь
зводиться до розв’язання найпростіших тригонометричних
рівнянь, які ми розглянули вище. Для цього застосовуються
відомі Вам тотожні перетворення, різні тригонометричні
формули, різні способи розв’язування алгебраїчних рівнянь,
формули скороченого множення и т.п.
Отже, запам’ятайте :
sin x a x 1 arcsin a k , k Z
k
cos x a x arccos a 2 n , n Z
tgx a x arctga p, p Z
ctgx a x arcctga l, l Z
a [–1;1]
a R

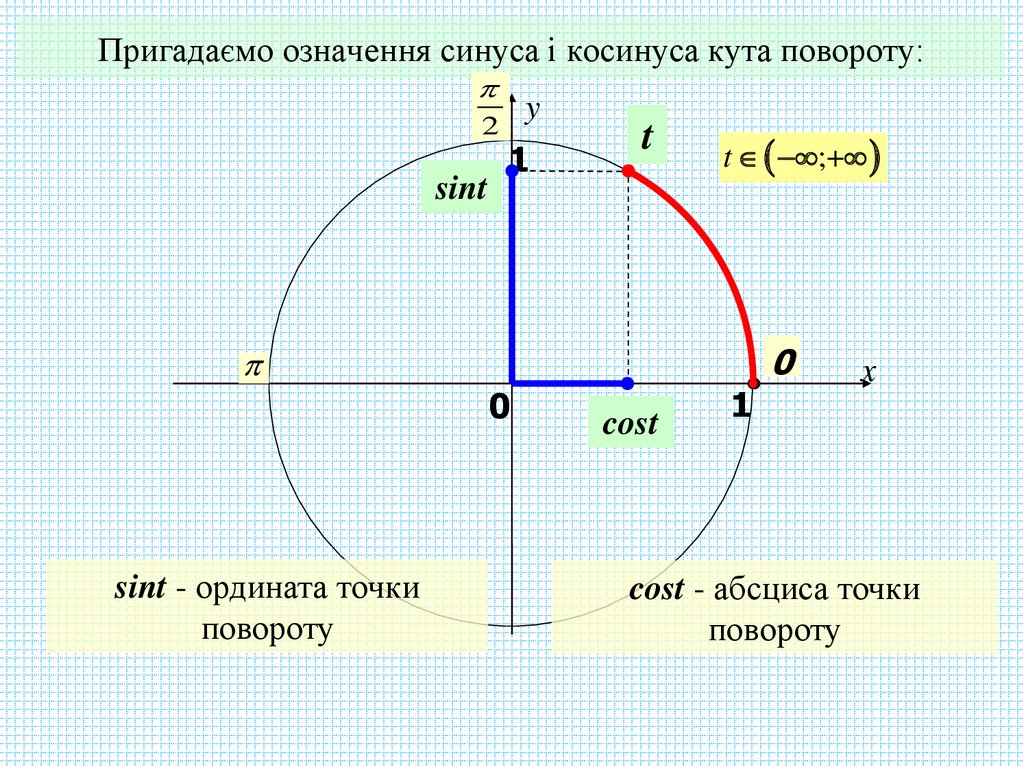
15. Пригадаємо означення синуса і косинуса кута повороту:

2
sint
y
1
t
0
0
sint - ордината точки
повороту
t ;+
cost
1
x
cost - абсциса точки
повороту

16.

Розв’яжемо рівняння
sint = a
за допомогою
тригонометричного кола:
–1
y
2
a >1
1
0
–1
3
2
2
a<–1
I випадок:
Якщо a [–1;1], то
рівняння sint = a не
має коренів.
0 x
1

17.

II випадок: Якщо a (–1;1),
то рівняння sint=a має два
корені на проміжку [0; 2 ],
який дорівнює періоду
функції синус.
y
2
1
a
t = –arcsina
–1
0
Отримані точки симетричні
відносно осі Оу. Значення
одніє з них відповідає числу
arcsina, а друга точка має
значення…? (визначте по
t = arcsinaмалюнку).
0 x
1 2
–1
3
2
2
arcsin a;
Отже, для t [0; 2 ] ми отримали два кореня: t arcsin a .

18.

Враховуючи періодичність функції y = sinx (Т=2 n, де n Z),
кожну з цих точок можна отримати при додаванні цілого числа повних
обертів, тобто:
t
sin t = a
arcsin a 2 k ;
k ,m Z ,
arcsin a 2 m;
Можна помітити, що у випадку, коли перед arcsina стоїть знак «+» до нього
додається парне(2k) число , а коли стоїть знак «–» додається непарне(2m+1)
число . Тому ці дві рівності можна об’єднати в одну формулу :
t 1 ·arcsin a n, n Z..
n
Ця формула дозволяє знайти корені найпростішого
тригонометричного рівняння sint = a у випадках, коли a (–1;1).

19.

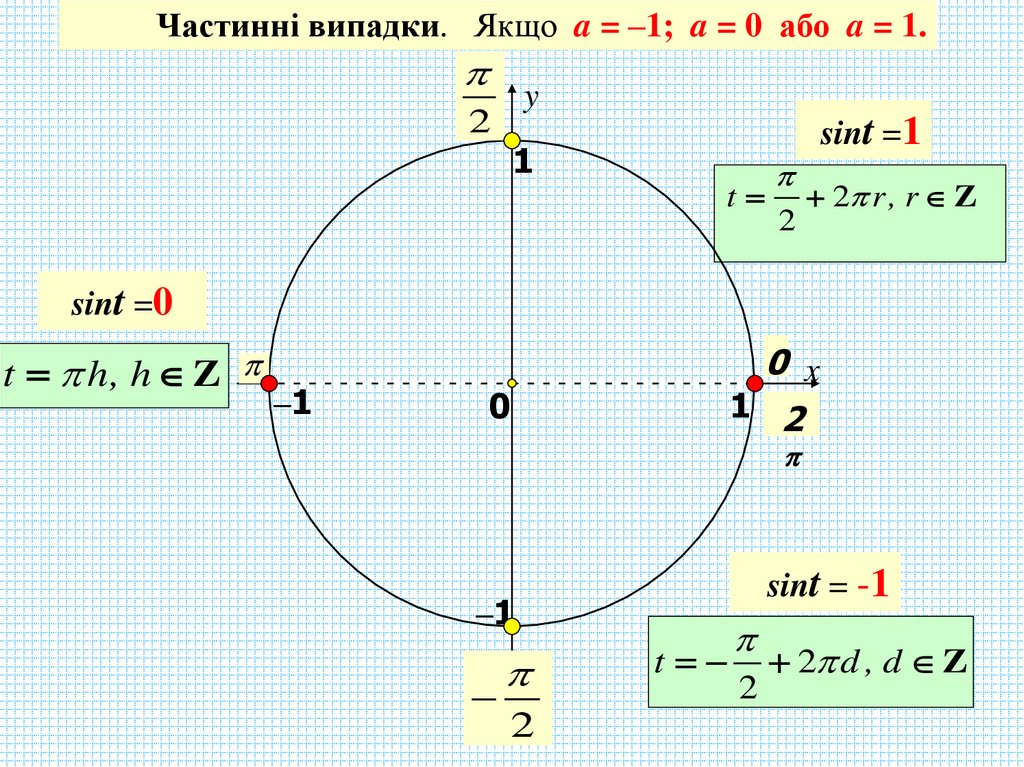
Частинні випадки. Якщо a = –1; a = 0 або a = 1.
y
2
1
sint =1
t
2
2 r , r Z
sint =0
t h, h Z
–1
0 x
1 2
0
sint = -1
–1
2
t
2
2 d , d Z

20.

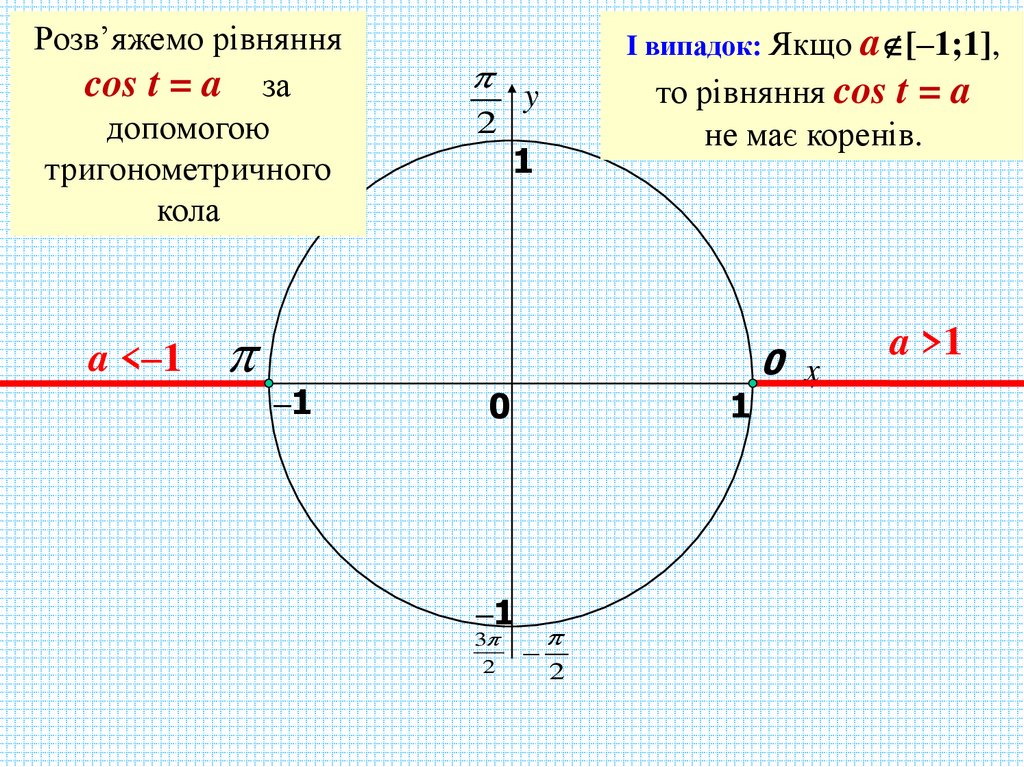
Розв’яжемо рівняння
cos t = a за
допомогою
тригонометричного
кола
a <–1
–1
2
a [–1;1],
то рівняння cos t = a
I випадок: Якщо
y
не має коренів.
1
1
0
–1
3
2
2
0 x
a >1

21.

II випадок:
a (–1;1), то рівняння
cos t = a має два корені
Якщо
y
2
на проміжку [0; 2 ], який
дорівнює періоду функції
косинус.
1
Отримані точки симетричні
відносно осі Оx. Значення
одніє з них відповідає числу
arccosa, а друга точка має
значення…?
t=arccosa
a
–1
0
0x
1 2
t= –arccosa
–1
3
2
2
arc co s a;
t
Отже, для t [0; 2 ] ми отримали два кореня:
arc co s a .

22.

Враховуючи періодичність функції y = сos x (Т=2 n, де n Z),
кожну з цих точок можна отримати при додаванні цілого числа повних
обертів, тобто:
cost = a
arc co s a 2 k ;
t
k ,m Z ,
arc co s a 2 m;
Ці записи відрізняються тільки знаками перед arccosa. Тому ці дві
рівності можна об’єднати в одну формулу :
t arc co s a 2 n, n Z..
Ця формула дозволяє знайти корені найпростішого
тригонометричного рівняння cost = a у випадках, коли
a (–1;1).

23.

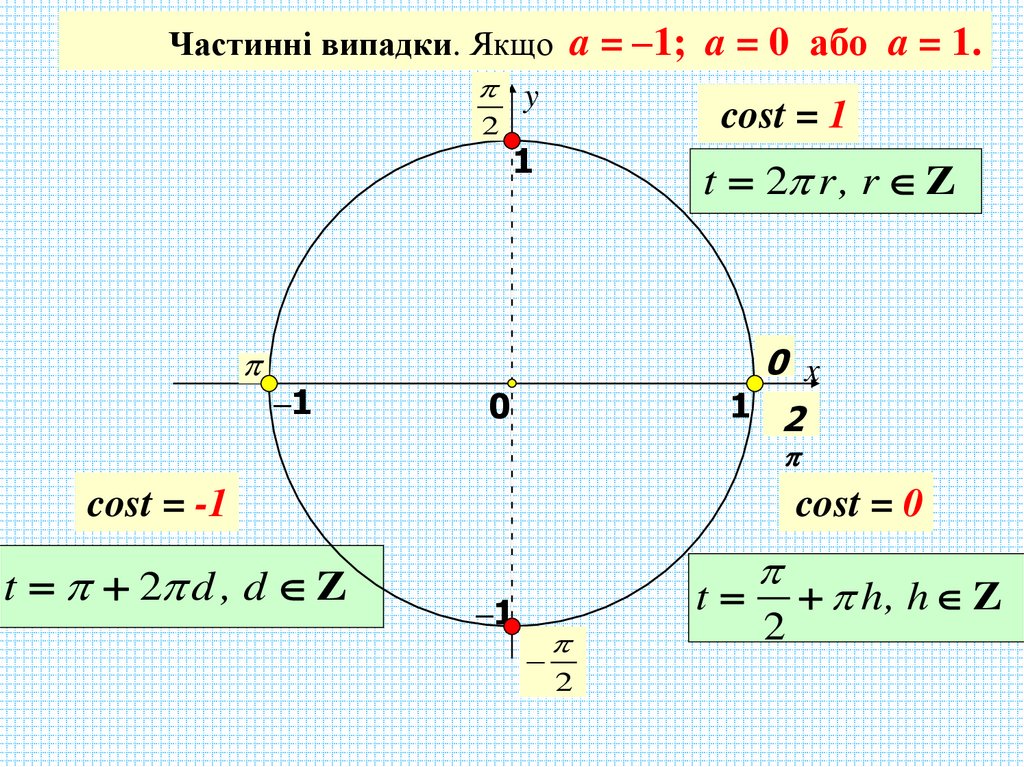
Частинні випадки. Якщо a = –1; a = 0 або a = 1.
y
2
–1
cost = 1
1
t 2 r, r Z
0 x
1 2
0
cost = -1
t 2 d , d Z
cost = 0
t
–1
2
2
h, h Z

24.

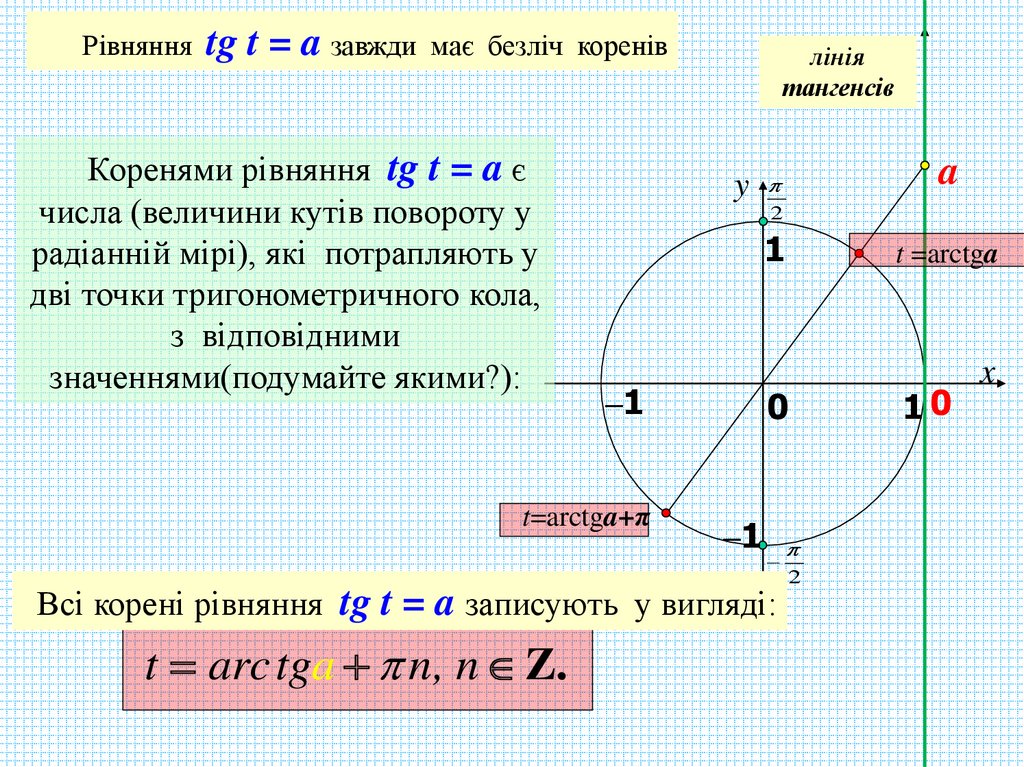
Рівняння
tg t = a завжди
має безліч коренів
Коренями рівняння tg t = a є
числа (величини кутів повороту у
радіанній мірі), які потрапляють у
дві точки тригонометричного кола,
з відповідними
значеннями(подумайте якими?):
лінія
тангенсів
y
2
1
–1
t=arctga+π
t =arctga
0
–1
Всі корені рівняння tg t = a записують у вигляді:
t arc tga n, n Z..
a
2
10
x

25.

y
0
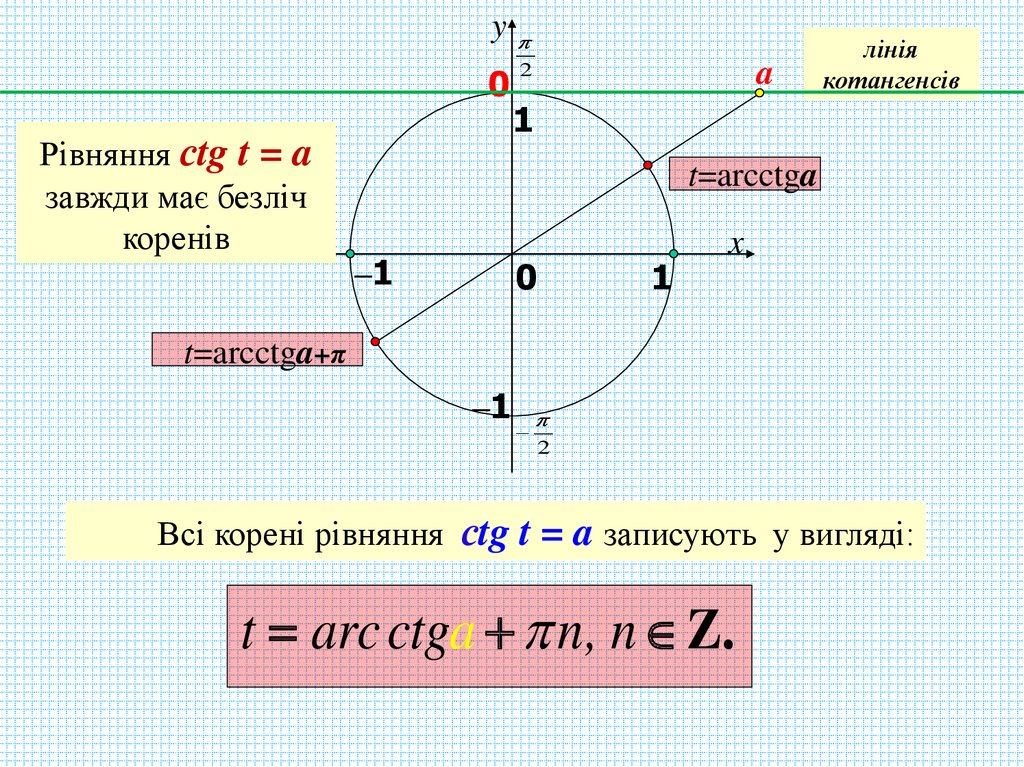
Рівняння сtg t = a
завжди має безліч
коренів
a
2
лінія
котангенсів
1
t=arcctga
–1
0
1
x
t=arcctga+π
–1
2
Всі корені рівняння сtg t = a записують у вигляді:
t arc ctga n, n Z..

26. Формули коренів найпростіших тригонометричних рівнянь

1. cost = а, де |а|≤ 1
t
t
або
Частинні випадки
1)
cost=0
t = π/2+πn‚ nєZ
2)
cost=1
t = 0+2πn‚ nєZ
3)
cost = -1
t = π+2πn‚ nєZ
2. sint = а, де |а| ≤ 1
або
3. tgt = а, аєR
t = arctg а + πk‚ kєZ
Частинні випадки
1) sint=0
t = 0+πk‚ kЄZ
2) sint=1
t = π/2+2πk‚ kЄZ
3) sint = - 1
t = - π/2+2πk‚ kЄZ
4. ctgt = а, аєR
t = arcctg а + πk‚ kєZ

27.

cos x a
x arccos a 2 m, m Z/.
sin x a
x 1 arcsin a m, m Z..
m

28.

ctg t = a
t arc ctga n, n Z..
sin x 1 x
2
2 n, n Z..

29.

30.

31.

Твій настрій:
Домашнє завдання:
Підручник Є.П. Нелін
Алгебра і початки аналізу
10 клас
Сторінка 334
№ 1, 2, 3, 4.
САМООЦІНКА:
ОЦІНКА ВЧИТЕЛЯ: