Елементи диференційного числення функції однієї та багатьох змінних. Інтегральне числення. Диференційні рівняння. Лекція 1

1.

Луганський державний медичний університет
Медична та біологічна фізика
1 семестр
Лекція 1
Елементи диференційного числення
функції однієї та багатьох змінних.
Інтегральне числення.
Диференційні рівняння.
Лектор – проф. Стрижаченко Олександр Володимирович

2. План лекції

Визначення похідної
Похідна та диференціал.
Таблиця похідних.
Необхідна умова диференційованості.
Геометричний сенс похідної.
Фізичний сенс похідної.
Основні правила обчислення похідних.
Невизначений інтеграл.
Методи інтегрування.
Диференційні рівняння.

3.

Похідна
Похідною функції f(x) у точці x=a
називають границю відношення приросту
функції до приросту аргументу коли
аргумент x наближається до точки a
f ( x) f (a)
f ' (a) lim
x a
x a

4.

Приклад
f ( x ) sin x
2sin
x a
x a
cos
2
2
x a
f ( x ) f (a )
sin x sin a
lim
lim
x a
x
a
x a
x a
x a
x a
x a
2sin
sin
2 (cos a ) lim
2 cos a
(cos a ) lim
x a
x a
x a
x a
2
f '(a ) lim
(sin x ) ' cos x

5.

Таблиця похідних
( const )' 0
( x )' n x
n
n 1
( a x )' a x ln a
( e x )' e x
(sin x)' cos x
(cos x)' sin x
1
(tg x)'
cos 2 x
1
(ctg x)' 2
sin x
1
(ln x )'
x
( arcsin x )'
1
1 x2
1
( arccos x )'
1 x2
1
( arctg x )'
1 x2
1
( arcctg x )'
1 x2

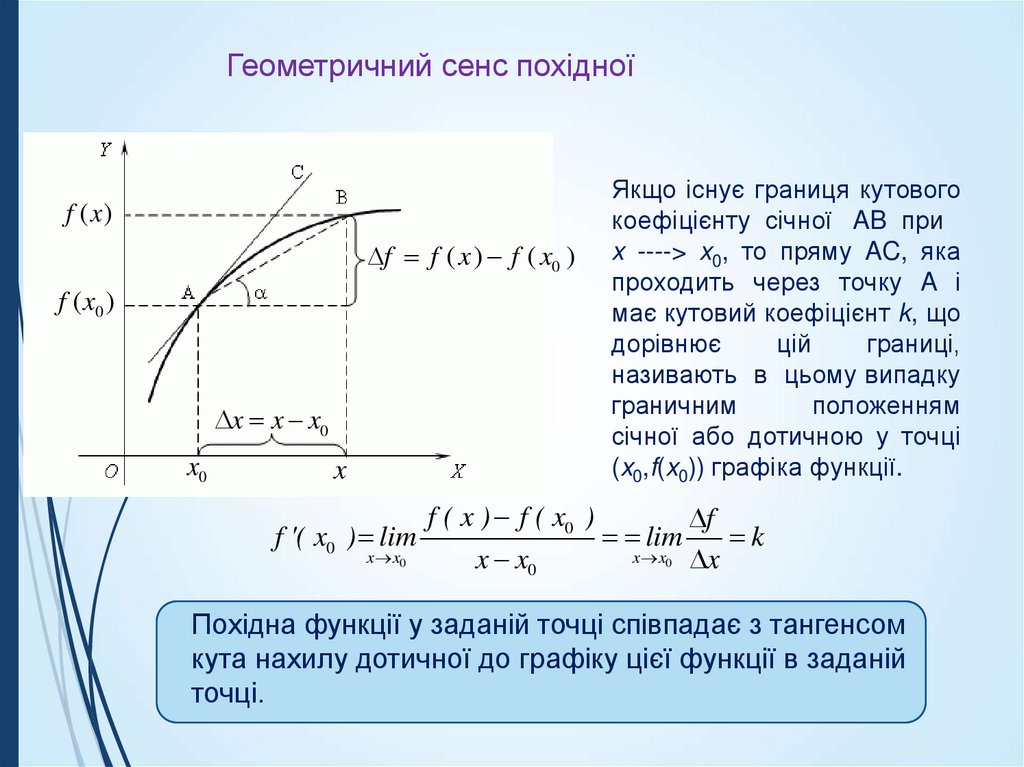
6. Геометричний сенс похідної

f (x )
f f ( x ) f ( x0 )
f ( x0 )
x x x0
x0
x
f '( x0 ) lim
x x0
Якщо існує границя кутового
коефіцієнту січної AB при
x ----> x0, то пряму AC, яка
проходить через точку A і
має кутовий коефіцієнт k, що
дорівнює
цій
границі,
називають в цьому випадку
граничним
положенням
січної або дотичною у точці
(x0,f(x0)) графіка функції.
f ( x ) f ( x0 )
f
lim
k
x
x
0 x
x x0
Похідна функції у заданій точці співпадає з тангенсом
кута нахилу дотичної до графіку цієї функції в заданій
точці.

7. Фізичний сенс похідної

Нехай матеріальна точка здійснює прямолінійний
рух і x(t) – її координата, яка відлічується від певної
точки на прямій, що прийнята за початок координат.
Середня швидкість руху за проміжок часу, що
пройшов з моменту t0 до моменту t , дорівнює
x (t ) x(t0 )
vср
.
t t0
Границя середньої швидкості при t ---> t0
називається у механіці міттевою швидкістю. За
визначенням похідної, міттева швидкість
x(t ) x(t0 )
v lim vср lim
x' (t0 ).
t t
t t
t t0
Ця інтерпретація узагальнюється на швидкість
зміни будь-якої фізичної величини.
0
0

8. Основні правила обчислення похідних

Похідна суми.
Похідна різниці.
Похідна добутку.
Похідна відношення (частки).
Похідна складної функції.

9. Правила диференціювання

Похідна постійної функції дорівнює нулю, тобто
C = 0, де С – константа.
Похідна суми (різниці) дорівнює сумі (різниці) похідних,
тобто
(u v) u v
Похідна добутку знаходиться за правилом:
(u v) u v u v
Зауваження. Формула диференціювання добутку може
бути легко узагальнена на випадок великої кількості
множників. Наприклад,
(u v w) u v w u v w u v w ,
(u v w t ) u v w t u v w t u v w t u v w t .

10. Правила диференціювання

(C u ) C u
, де С – константа.
постійний множник виноситься за знак похідної
Похідна відношення знаходиться за правилом:
u u v u v
v
v2
v( x) 0 .

11.

Похідна складної функції
Розглянемо складну функцію
F ( x ) f ( ( x )).
Якщо існують похідні
'( x0 ), f '( ( x0 )),
то її похідна визначається за формулою
F ' ( x0 ) f ' ( ( x0 )) ' ( x0 ).

12.

Дифференциал
На практиці зазвичай прийнято записувати
всі формули, до яких входить похідна або
диференціал, не вводячи спеціального
позначення для фіксованої точки a, а
використовують
для
неї
традиційне
позначення x . В цьому випадку неявно
вважається наявність ще одного символу
для позначення незалежної змінної, який не
пишеться. Це дозволяє записати останню
формулу у вигляді рівності
df ( x) f ' ( x)dx.

13.

Таблиця диференціалів
d (const) 0 d( x ) x 1dx d( a x ) a x ln a dx d(log a x )
d (sin x) cos x dx
d (cos x) sin x dx
dx
d(tg x)
cos 2 x
dx
d (ctg x) 2
sin x
d (arcsin x)
dx
1 x
dx
d (arccos x)
1 x2
dx
d (arctg x)
1 x2
dx
d (arcctg x)
1 x2
2
dx
x ln a
d (sh x ) ch x dx
d (ch x ) sh x dx
dx
d (th x ) 2
ch x
dx
d (cth x ) 2
sh x

14. Похідні вищих порядків

Введемо поняття похідної другого порядку
функції f x . Похідну від першої похідної
функції f x , тобто y ' ' будемо називати
похідною другого порядку (тоді y ' - похідна
першого порядку) і будемо її позначати y ' '
або f ' ' x . Далі y ' ' y ' ' ' f ' ' ' x - це
похідна третього порядку, … а
y y
n 1 /
n
- це похідна n-го порядку.

15. Функції багатьох змінних

16. Визначення функції двох змінних

Визначення. Якщо кожній парі (x,y)
значень двох незалежних одна від одній
змінних величин x і y з певної множини
D відповідає єдине значення величини
z, а кожному z відповідає хоча б одна
пара (x,y), то ми говоримо, що z є
функцією двох незалежних змінних x і y,
яка визначена у D.

17. Позначення

При цьому пишуть:
z f ( x, y ), z ( x, y ), z z ( x, y ).
Якщо парі чисел ( x0 , y 0 ) D відповідає число z 0 L ,
то пишуть
Або
z 0 f ( x0 , y 0 )
z 0 z x x0
y y0
z 0 називається окремим значенням функції
при x x , y y .
0
0

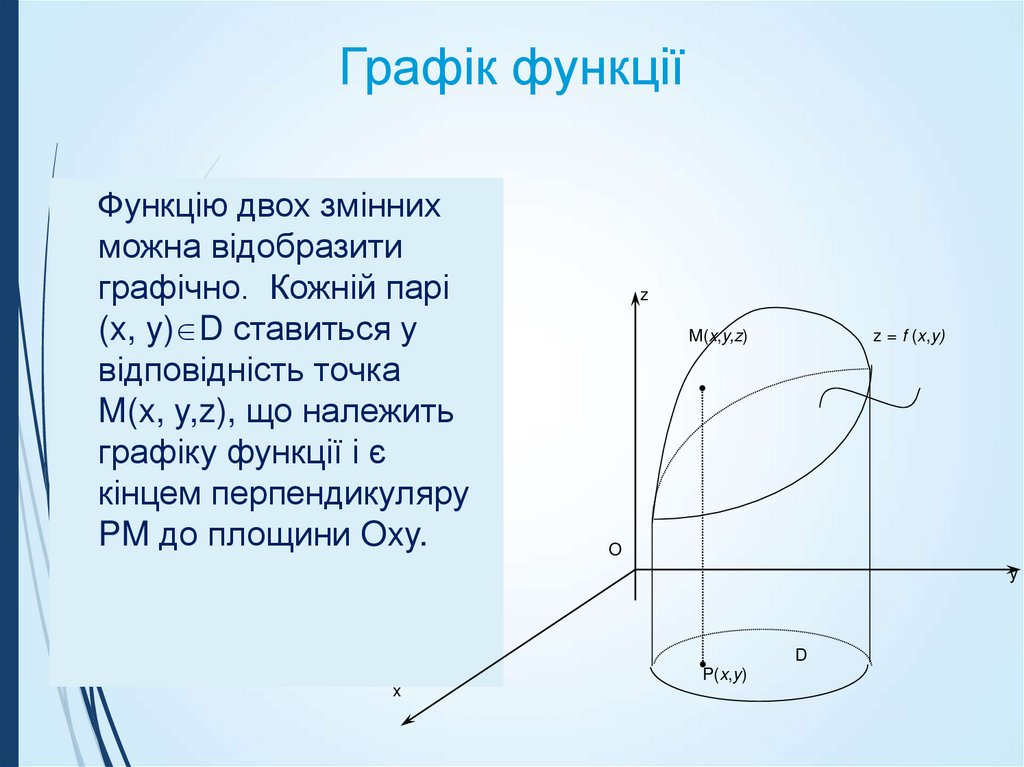
18. Графік функції 2-х змінних

Геометричне місце точок,
координати яких задовільнять
рівнянню z = f(x,y), називається
графіком функції двох змінних.

19. Графік функції

Функцію двох змінних
можна відобразити
графічно. Кожній парі
(x, y) D ставиться у
відповідність точка
M(x, y,z), що належить
графіку функції і є
кінцем перпендикуляру
PM до площини Oxy.
z
M(x,y,z)
z = f (x,y)
O
y
D
P(x,y)
x

20. Частинні похідні

Частинна похідна (першого порядку)
функції z = f (x, y) по змінній x по
z
z x
f x ( x, y )
x
Аналогічно позначається частинна
похідна функції z = f (x, y) по змінній y:
z
z y
f y ( x, y )
y

21. Приклад

Знайдемо частинні похідні функції
z 4x y x y x y
2
3
2
Отримуємо
2
2
z X 8 xy 3x y 2 xy ,
z Y 4 x 2 x 3 2 x 2 y.
2

22.

Первісна. Невизначений інтеграл.
Заміна змінної в невизначеному інтегралі. Формула
інтегрування по частинам.

23.

Основні визначення
Визначення 1. Функція F ( x) називається
первісною по відношенню до функції f ( x)
на певному проміжку, якщо на цьому
проміжку функція F ( x) диференційована
і задовільніє умові F ( x) f ( x) або,
що є таким самим, dF ( x) f ( x)dx.

24.

Основні визначення, приклади
Операція переходу до первісної має свою назву невизначене інтегрування, і позначається: f x dx.
Визначення. Сукупність всіх первісних
функції f x називається її невизначеним інтегралом
і позначається f x dx F x C , де С R, а вираз
f x dx називається підінтегральним виразом,
f x - підінтегральною функцією.

25.

Таблиця невизначених інтегралів
x 1
1. x dx
С , 1.
1
6.
dx
ctg x С.
2
sin x
dx
ln x С.
x
7.
dx
tg x С.
cos 2 x
ax
3. a dx
С.
ln a
8.
arcsin x C
.
2
arccos
x
C
1 x
1
4. sin xdx cos x С.
arctg x С
dx
9.
.
1 x 2 arcctg x C1
2.
x
5. cos xdx sin x С.
dx

26.

Таблиця невизначених інтегралів
Окремі випадки
dx
1
x2 x C
dx
x 2 x C
x
x
e
dx
e
C

27.

Основні правила обчислення інтегралів
1. f x g x dx f x dx g x dx
Доведення.
f x dx g x dx f x dx g x dx f x g x
f
x
g
x
dx
f x g x
2. af x dx a f x dx
Доведення.
af
x
dx
af x
a f x dx af x

28.

Основні правила обчислення інтегралів
Теорема. (Заміна змінних у невизначеному інтегралі)
Якщо функція y f x неперервна на X , а x t , t T , t C 1 T ,
(тобто t неперервна разом з t і t має зворотню
функцію), тоді інтеграл f x dx f t t dt
Додедення. Покажемо, що ліва і права частини мають рівні
похідні по одному й тому ж аргументу.
d
f x dx f x
dx
d
d
dt
1
f
t
t
dt
f
t
t
dt
f
t
t
f x .
dx
dt
dx
t
Таким чином, інтеграли у лівій і правій частинах рівні.

29.

Інтегрування частинами
Інтегрування частинами.
За правилом диференціювання добутку
d uv udv vdu udv d uv vdu , звідки
udv uv vdu
Останнє співвідношення називається
формулою інтегрування частинами.

30.

Класи функцій, що інтегруються частинами
arcsin x
arccos x
3. J Pn x
dx , де Pn x - багаточлен.
arctg x
arcctg x
dv Pn x dx, u arcsin x arccos x; arctg x; arcctg x .

31.

Класи функцій, що інтегруються частинами
4. J Pn x ln x dx ,
k
де Pn x - багаточлен.
dv Pn x dx, u ln x
k

32. Диференційні рівняння

Визначення диференційного рівняння (ДР). Загальний та
частинний розв’язок ДР.
ДИФЕРЕНЦІЙНІ РІВНЯННЯ ПЕРШОГО ПОРЯДКУ
ДР з розділеними змінними. Алгоритм розв’язку
Однорідні ДР. Алгоритм розв’язку
Лінійні ДР. Алгоритм розв’язку методом Бернуллі
ДИФЕРЕНЦІЙНІ РІВНЯННЯ ВИЩИХ ПОРЯДКІВ
Лінійні однорідні ДР

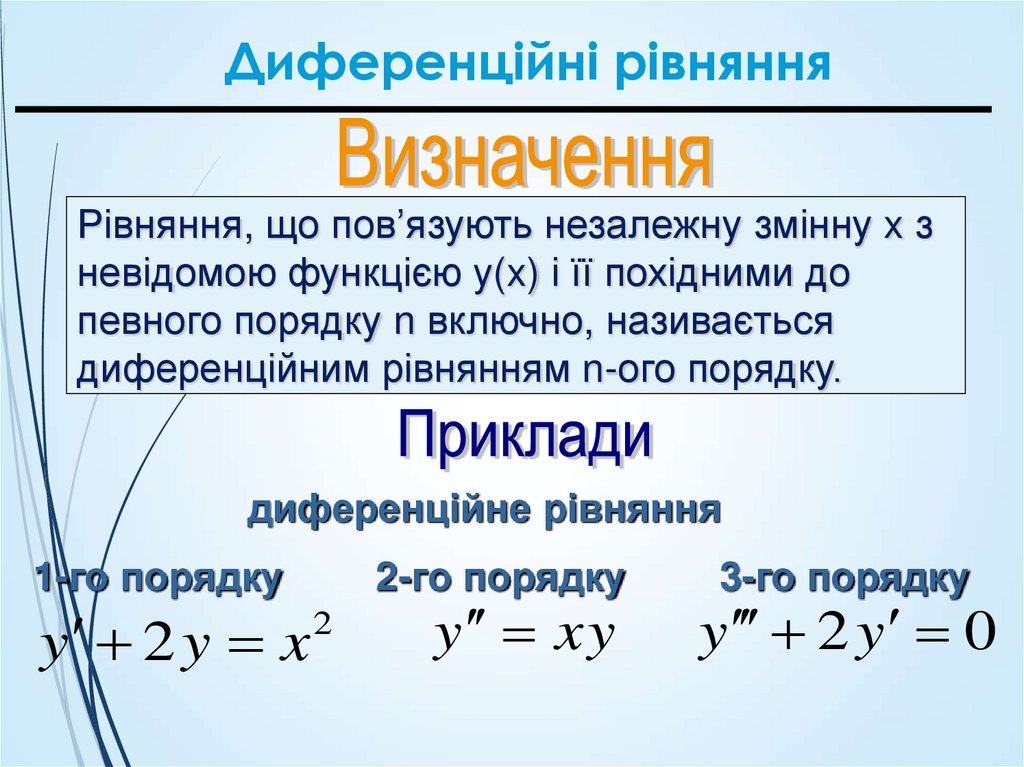
33. Диференційні рівняння

Рівняння, що пов’язують незалежну змінну x з
невідомою функцією y(x) і її похідними до
певного порядку n включно, називається
диференційним рівнянням n-ого порядку.
диференційне рівняння
1-го порядку
y 2 y x
2-го порядку
2
y xy
3-го порядку
y 2 y 0

34.

Диференційні рівняння
ЗАГАЛЬНИЙ ВИГЛЯД ДИФЕРЕНЦІЙНОГО
РІВНЯННЯ n-ОГО ПОРЯДКУ
F ( x, y, y ,..., y
( n)
) 0
(1)
n 1
F – певна функція від n+2 змінних,
x – незалежна змінна, y(x) – функція, яку шукаємо
y ( x),..., y ( n ) ( x) - її похідні
Диференційне рівняння n-ого порядку
називається розв’язаним відносно старшої
похідної, якщо воно має вигляд:
(n)
( n 1)
y
f ( x, y, y ,..., y
)

35. Диференційні рівняння

Розв’язком диференційного рівняння (1)
називається функція y(x), яка має похідні до
n-ого порядку включно, і така, що її
підстановка у рівняння (1) перетворює його у тотожність
Розв’язком рівняння y 2 y є функция
y ( x) e
2x
2x
y (e ) 2e
2x
2x
2
e
2
e
2x
y e
2x

36. Диференційні рівняння

Задача щодо знаходження розв’язку певного
диференційного рівняння називається задачою
інтегрування даного диференційного рівняння
График розв’язку диференційного рівняння
називається інтегральною кривою
Загальним розв’язком диференційного рівняння (1)
n-ого порядку називається такий його розв’язок
y ( x, с1 , с2 ,..., сn )
який є функцією змінної x та n довільних
незалежних сталих с1 , с2 ,..., сn

37. Диференційні рівняння 1 порядку

ЗАГАЛЬНИЙ ВИГЛЯД ДИФЕРЕНЦІЙНОГО РІВНЯННЯ 1-ОГО ПОРЯДКУ
F ( x, y, y ) 0
(2)
ДИФЕРЕНЦІЙНЕ РІВНЯННЯ 1-ОГО ПОРЯДКУ, ЯКЕ РОЗВ’ЯЗАНЕ ВІДНОСНО
СТАРШОЇ ПОХІДНОЇ
y f ( x, y )
(3)
f – певна функція двох змінних

38. Диференційні рівняння з розділеними змінними

ДИФЕРЕНЦІЙНЕ РІВНЯННЯ З РОЗДІЛЕНИМИ ЗМІННИМИ
P( x)dx Q( y )dy 0
(5)
- ЗАГАЛЬНИЙ ІНТЕГРАЛ
P(
x
)dx
Q(
y
)dy
C
рівняння з розділеними змінними
e dx ( y 1)dy 0
x
загальний інтеграл
2
y
e dx ( y 1)dy 0 e 2 y c
x
x

39. Диференційні рівняння з розділеними змінними

ДИФЕРЕНЦІЙНЕ РІВНЯННЯ З РОЗДІЛЕНИМИ ЗМІННИМИ
P1 ( x) Q1 ( y)dx P2 ( x) Q2 ( y)dy 0 (6)
Рівняння (6) зводится до рівняння (5) шляхом
почленного ділення на Q1 ( y) P2 ( x) 0
P1 ( x )
Q2 ( y )
dx
dy 0
P2 ( x )
Q1 ( y )
P1 ( x )
Q2 ( y )
- ЗАГАЛЬНИЙ ІНТЕГРАЛ
dx
dy
C
P2 ( x ) Q1 ( y )

40. Приклад

y
y , y ( 4) 1
x
dy
y dy
dx
ln y c1 ln x ln c ln x
dx
x
y
x
c - загальний розв’язок
y
x
c
4
y (4) 1 1 c 4 y - частинний розв’язок
4
x

41. Лінійні диференційні рівняння 1-ого порядку

Диференційне рівняння першого порядку
називається лінійним, якщо його можна записати
y p( x) y g ( x) (9)
у вигляді
де p(x) і g(x) – задані функції
функція y і її похідна y
входять у рівняння окремо одна від іншої
МЕТОДИ ІНТЕГРУВАННЯ ДИФЕРЕНЦІЙНОГ РІВНЯННЯ (9)
МЕТОД БЕРНУЛЛІ
МЕТОД ЛАГРАНЖА

42. Приклад

2y
2
y
5x
x
y u v y u v u v
2
2
2
2
u v u v uv 5 x u v u (v v) 5 x
x
x
2
dv
2
1
v v 0
dx ln v 2 ln x ln 2
x
v
x
x
1
1
2
4
5
v 2 u 2 5 x u 5 x u x c
x
x
1
c
5
3
y ( x c) 2 x 2
x
x

43. Лінійні однорідні диференційні рівняння 2-ого порядку зі сталими коефіцієнтами

y py qy 0 (4)
p, q – дійсні числа
ЗАГАЛЬНИЙ РОЗВ’ЯЗОК РІВНЯННЯ (4)
yо ( x ) с1 y1 ( x ) с2 y2 ( x ) (5)
y1 ( x), y2 ( x) - частинні розв’язки (4)
с1 , с2 - довільні числа

44. Лінійні однорідні диференційні рівняння 2-ого порядку зі сталими коефіцієнтами

МЕТОД ЕЙЛЕРА
Розв’язок рівняння (4) будему шукати у вигляді:
y( x) e , - невідоме число
x
x
2 x
y ( x) e , y ( x) e
Підставимо розв’язок у рівняння (4):
2 x
x
x
e p e qe 0
Отримаємо характеристичне рівняння
p q 0
2
(6)

45. Лінійні однорідні диференційні рівняння 2-ого порядку зі сталими коефіцієнтами

p q 0
2
(6)
Виподок 1:
D p 4q 0
2
1 , 2 - два різних дійсних кореня рівняння (6)
1 x
y1 ( x) e
2 x - розв’язки рівняння (4)
y2 ( x ) e
1 x
2 x
(7)
yо ( x ) с1 e с2 e

46. Лінійні однорідні диференційні рівняння 2-ого порядку зі сталими коефіцієнтами

p q 0
2
(6)
Випадок 2:
D p 4q 0
p
1 2 - розв’язки рівняння (6)
p 2
x
2
y1 ( x) e
y2 ( x) xe
2
p
x - розв’язки рівняння (4)
2
p
p
x
x
(8)
2
2
о
1
2
y ( x ) с e
с xe

47. Лінійні однорідні диференційні рівняння 2-ого порядку зі сталими коефіцієнтами

p q 0
2
(6)
D p 4q 0
p
D - два різних комплексних
1, 2 i
2
4 розв’язка рівняння (6)
2
Випадок 3:
p
,
x
2
y1 ( x) e sin x
y2 ( x) e cos x
x
x
D
4
- розв’язки рівняння (4)
x
yо ( x ) с1 e sin x с2 e cos x (9)

48. Приклад

y 2 y 2 y 0
2 2 0
D 4 8 4 0
2
2 2i
1, 2
1 i
2
y1 e sin x,
x
y2 e cos x
x
yоо ( x) с1e sin x с2 e cos x
x
x

49. Література

1. Минорский В.П.
«Сборник задач по высшей математике».
«Наука», 1971, 852 с.
2. Стрижаченко А.В. та ін.
«Высшая математика и статистика».
Харьков, НФаУ, 2017, 232 с.
3. Гобуненко Б.Ф. та ін.
«Теорія ймовірностей і статистичні методи обробки
результатів спостережень».
Харків, НФаУ, 2002, 188 с.
4. Гмурман В.Е.
«Теория вероятностей и математическая статистика».
Учебное пособ. для вузов. 1998, 479 с.
5. Гмурман В.Е.
«Руководство по решению задач по теории вероятностей
и математической статистики».
Учебное пособ. для вузов. 1998, 400 с.

50. Дякую за увагу

50
Дякую за
увагу