Similar presentations:
Поняття похідної функції. Основні правила диференціювання. Таблиця похідних
1. ВИЩА МАТЕМАТИКА
для студентів ОКР “Бакалавр”Напрям підготовки:
6.050701 - “Електротехніка та електротехнології”
Автор:
Доцент кафедри вищої та прикладної математики
Шостак Сергій Володимирович
2. Тема1: Поняття похідної функції, її геометричний та механічний зміст. Основні правила диференціювання. Таблиця похідних.
1. Означення похідної2. Геометричний зміст похідної
3. Механічний зміст похідної
4. Залежність між неперервністю
і диференційовністю функції
5. Основні правила диференціювання
6. Похідні від основних
елементарних функцій
3. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
Поняття похідної є одним з основних понятьматематичного аналізу. Розділ математики, в
якому вивчається поняття похідної та її
застосування до дослідження функцій, називають
диференціальним численням.
4. ОСНОВОПОЛОЖНИКИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ
І. НьютонГ. Лейбніц
5. ЗАДАЧІ, ЩО ПРИВЕЛИ ДО ПОНЯТТЯ ПОХІДНОЇ
ЗАДАЧІпро миттєву
швидкість
про дотичну
до кривої
6. Означення похідної
Означення. Похідною функції зааргументом х називається границя
відношення приросту функції до
приросту аргументу, коли приріст
аргументу прямує до нуля.
7. Означення похідної (аналітичний вигляд)
f ( x + Dx ) - f ( x )Dy
y¢ = lim
= lim
Dx ®0 Dx
Dx ® 0
Dx
8. ПОЗНАЧЕННЯ ПОХІДНОЇ
y ¢, y ¢x , f ¢( x ) ,позначення
Лагранжа
dy df ( x ) d
,
, f ( x)
dx dx
dx
позначення
Лейбніца
9. ЗМІСТ ПОХІДНОЇ
ГЕОМЕТРИЧНИЙМЕХАНІЧНИЙ
ЕЛЕКТРИЧНИЙ
10.
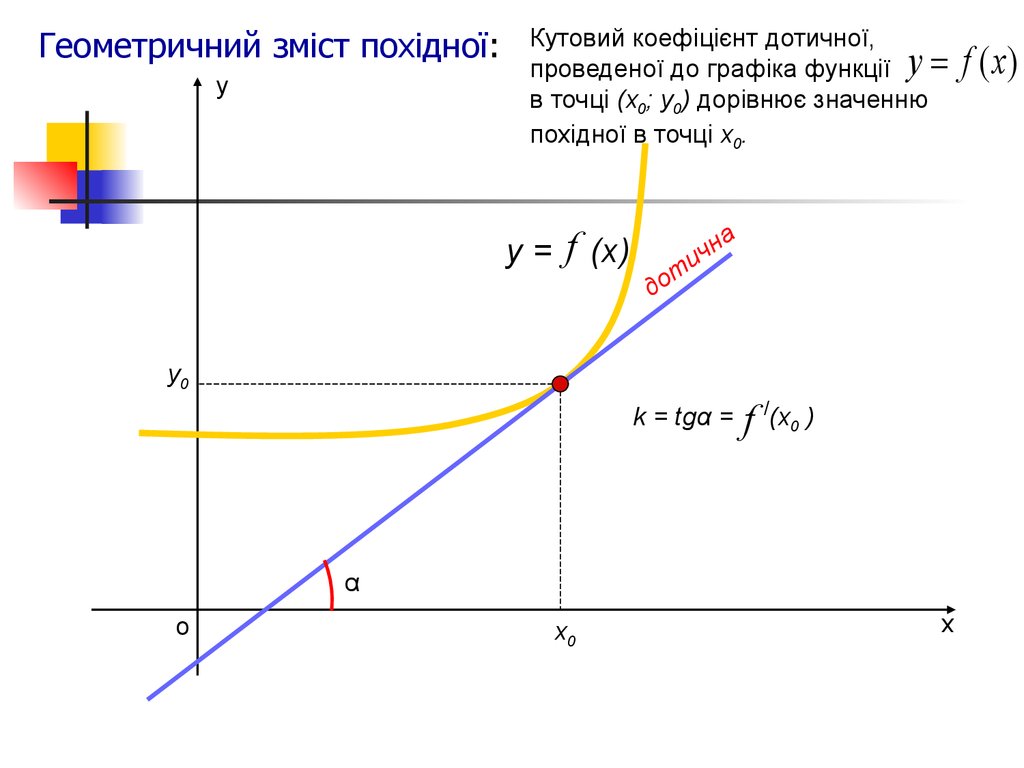
Геометричний зміст похідної:у
Кутовий коефіцієнт дотичної,
проведеної до графіка функції y =
в точці (х0; у0) дорівнює значенню
похідної в точці х0.
y = f (x)
на
ч
ти
о
д
у0
k = tgα =
f /(x
0
)
α
о
х0
х
f ( x)
11.
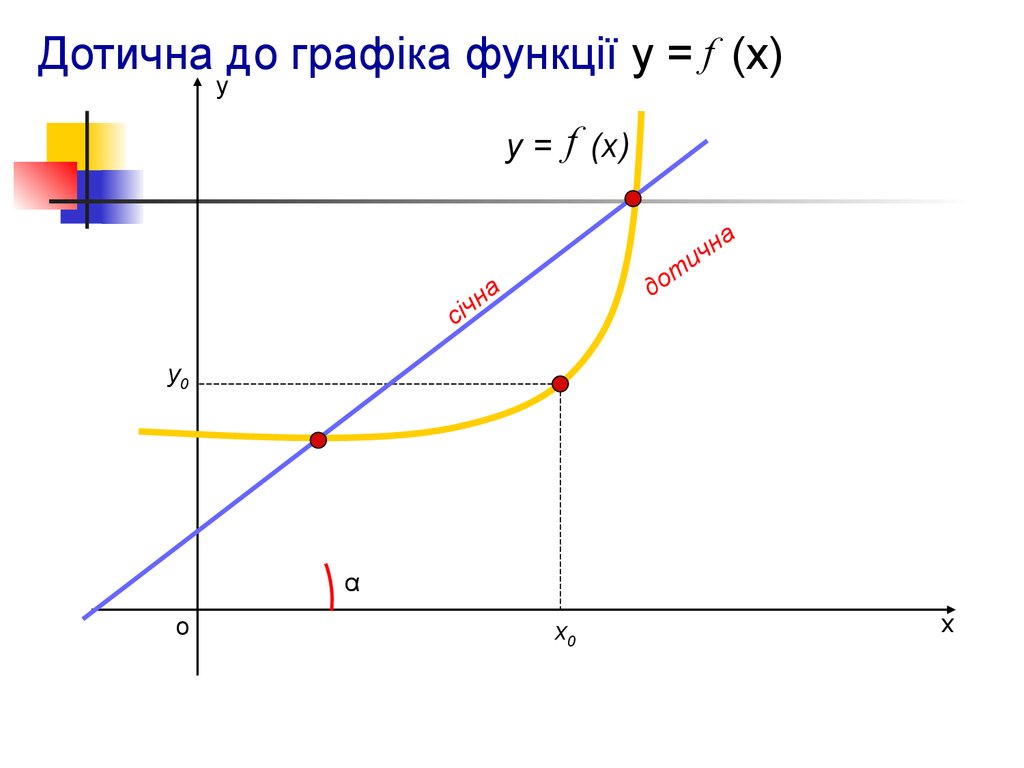
Дотична до графіка функції у = f (х)у
y = f (x)
на
ч
ти
о
д
а
н
ч
сі
у0
α
о
х0
х
12.
Дотична до графіка функції у = f (х)у
у0
А
y = f (x)
α
о
х0
х
13.
/Рівняння дотичної: у = f (х0) + f (х0)(х – х0).
у
y = f (x)
у0
k = tgα =
f /(x
0
)
α
о
х0
у0 = f (х0)
х
14. Механічний зміст похідної:
v(t0) = x (t0)/
a(t0) = v (t0)
/
х0 – координата точки
v(t0)- швидкість точки в момент
часу t0
а(t0) – прискорення точки
в момент часу t0
15. ЕЛЕКТРИЧНИЙ ЗМІСТ ПОХІДНОЇ
Нехай Q = Q(t ) - кількість електрики, якапройшла через поперечний переріз
провідника за час t . Сила струму i (t ) в
момент часу t є похідна від кількості
електрики Q(t ) по часу t , тобто
i (t ) = Q¢(t )
16.
Похідна функцій y = C , y = x , y = xy = C (const )
y' =
y=x
y' =
y= x
y' =
1
2 x
17.
Похідна степеневої функціїy=x
n
y' = n x
n -
18.
Похідна показникової функціїy=a
x
y ' = a ln a
x
y=e
x
y' = e
x
19.
Похідна логарифмічних функційy = log a x
y' =
x ln a
y = ln x
y' =
x
20.
Похідна тригонометричних функційy = sin x
y ' = cos x
y = cos x
y ' = - sin x
y = tgx
y' =
cos x
y = ctgx
y' =
sin x
21.
Похідні від обернених тригонометричнихфункцій
y = arcsin x
y' =
- x
y = arctgx
y' =
+ x
y = arccos
y' = - x
y = arcctgx
y' =
+ x
22.
Похідна складеної функціїy = f ( ( x))
y ' = f ' ' x
Приклад:
y = sin ln
x
x
y ' = cos ln
x ln
x
ln
x
23.
Формула похідної сумиy =u+v
y ' = u '+ v '
Приклад:
y = x + x + x
y ' = x + x +
24.
Формула похідної добуткуy = u v
y ' = u ' v + u v'
Приклад:
y = cos x log x
y ' = - sin x log x + cos x
x ln
25.
Формула похідної часткиu
y=
v
u ' v - u v '
y' =
v
Приклад:
arcsin x
y=
ln x
ln x - arcsin x
x
x
y' =
ln x
26. Контрольні запитання
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Означення похідної.
Алгоритм знаходження похідної за означенням.
Фізичний зміст похідної.
Геометричний зміст похідної.
Електричний зміст похідної.
Похідна суми.
Похідна добутку.
Похідна частки.
Похідна складеної функції.
Похідна функції
y = e xx.
y=a.
Похідна функції
Похідна логарифмічної функції.
Похідна степеневої функції.
Похідні тригонометричних функцій.
Похідні обернених тригонометричних функцій.






















 mathematics
mathematics








