Similar presentations:
Дійсні числа
1.
2. §1. Дійсні числа
Глава 4Вступ до математичного аналізу
§1. Дійсні числа
• 1.1. Множини. Логічні символи
x X,
A a1 , a2 ,..., an
A B
a X
X x1, x2 ,..., xn ,...
A B
3.
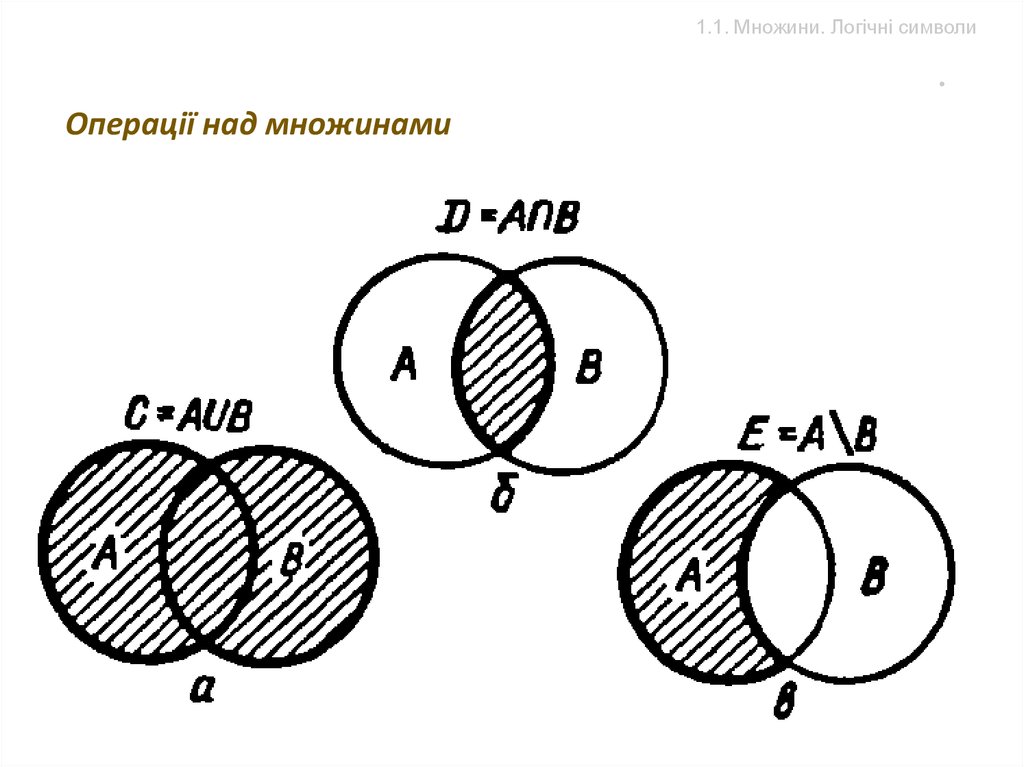
1.1. Множини. Логічні символиОперації над множинами
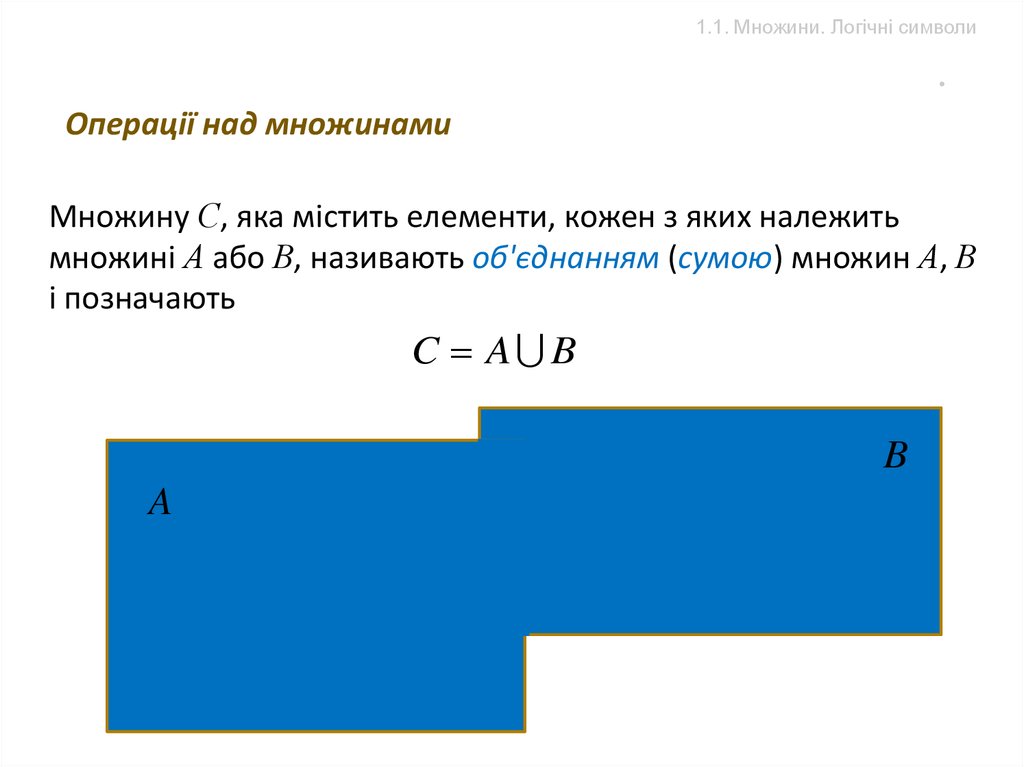
Множину С, яка містить елементи, кожен з яких належить
множині А або В, називають об'єднанням (сумою) множин А, В
і позначають
C A B
B
A
4.
1.1. Множини. Логічні символиОперації над множинами
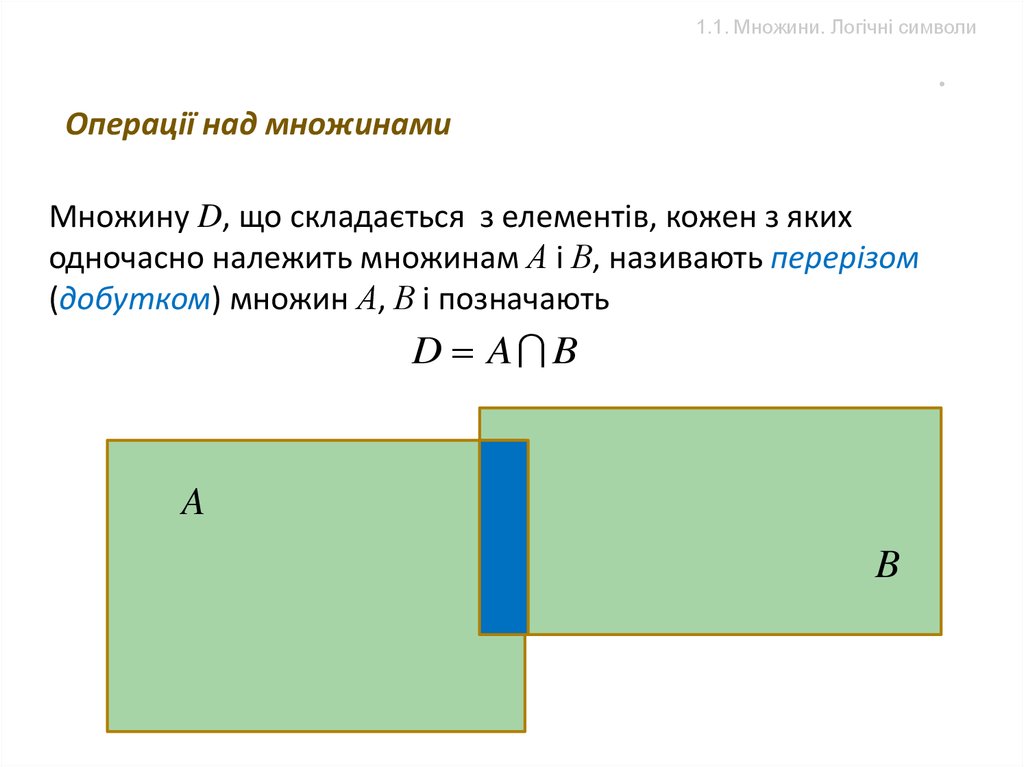
Множину D, що складається з елементів, кожен з яких
одночасно належить множинам А і В, називають перерізом
(добутком) множин А, В і позначають
D A B
A
B
5.
1.1. Множини. Логічні символиОперації над множинами
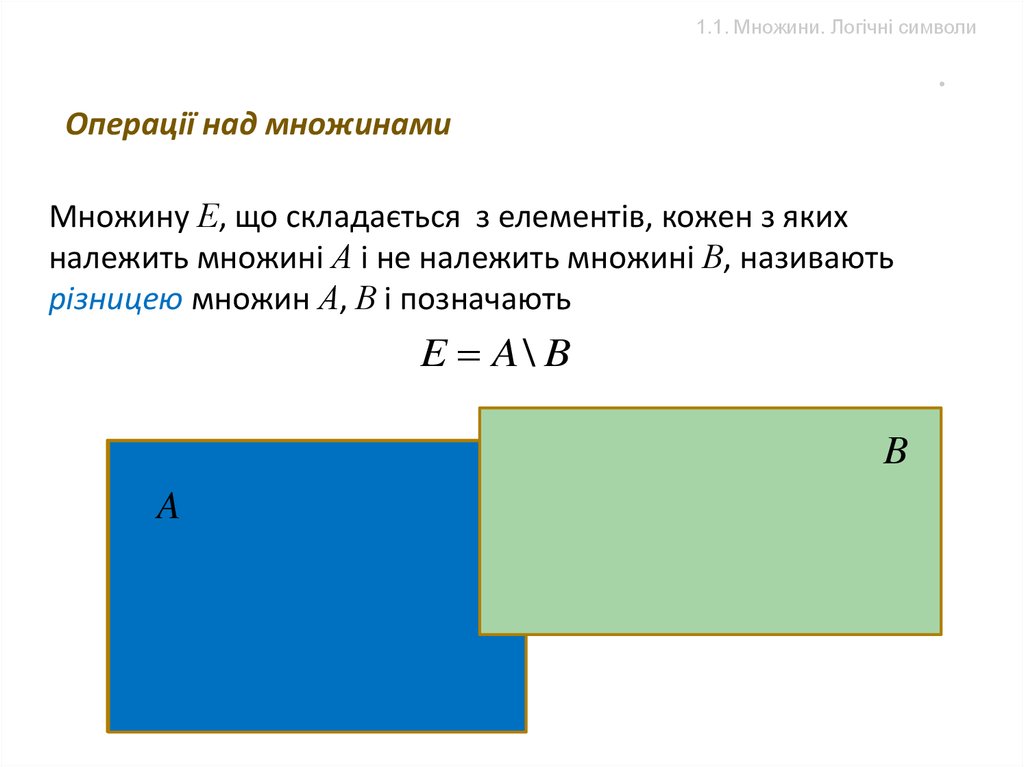
Множину Е, що складається з елементів, кожен з яких
належить множині А і не належить множині В, називають
різницею множин А, В і позначають
E A\ B
B
A
6.
1.1. Множини. Логічні символиОперації над множинами
7.
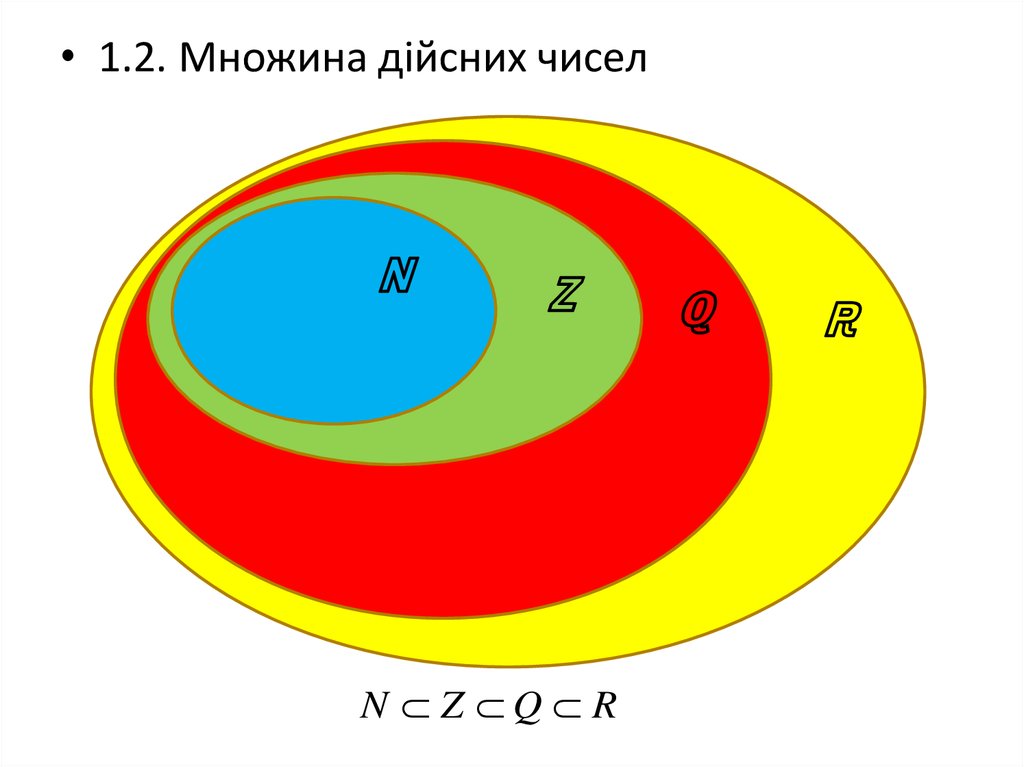
• 1.2. Множина дійсних чиселℕ
ℤ
N Z Q R
ℚ
ℝ
8.
• 1.3. Числові проміжки. Окіл точкиa, b
a, b
, b
, b
a, b
a, b
a,
a,
a, b
Околом точки x0 називають будь-який інтервал ( , ), що
містить цю точку.
Інтервал (x0 ; x0+ ) називають околом точки x0.
9.
• 1.4. Модуль (абсолютна величина) дійсногочисла
x, x 0;
x 0, x 0;
x , x 0.
10.
§2. Функції11. Поняття функції
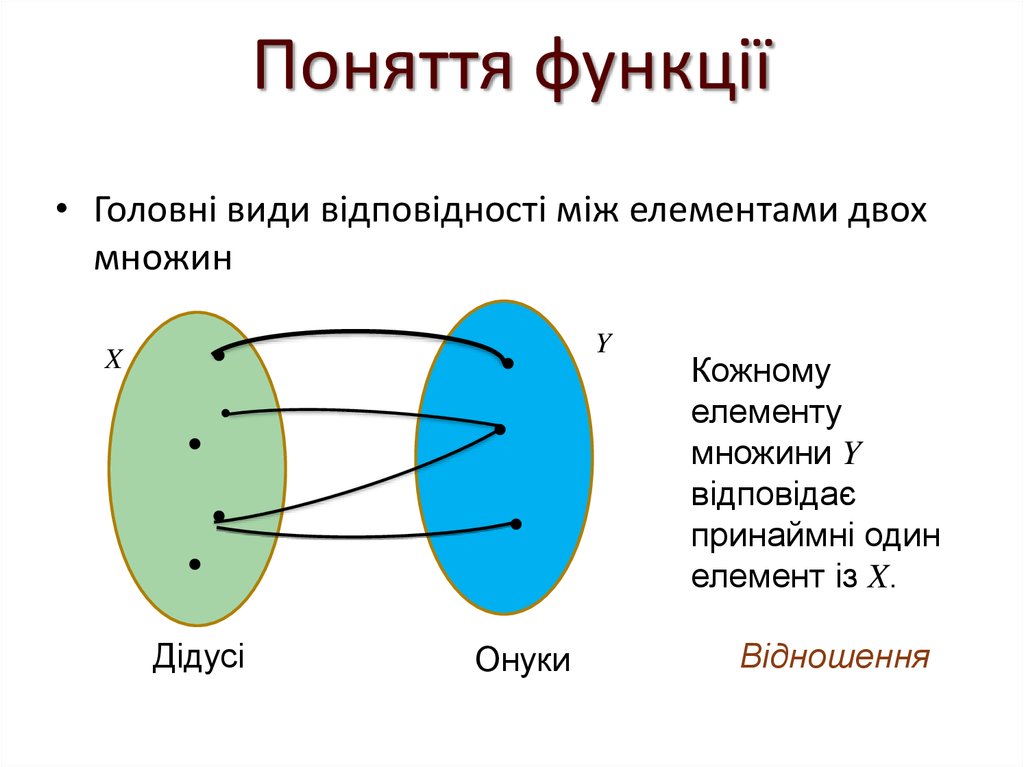
• Головні види відповідності між елементами двохмножин
Сюр’єкція
Y
X
Дідусі
Онуки
Кожному
елементу
множини Y
відповідає
принаймні один
елемент із X.
Відношення
12. Поняття функції
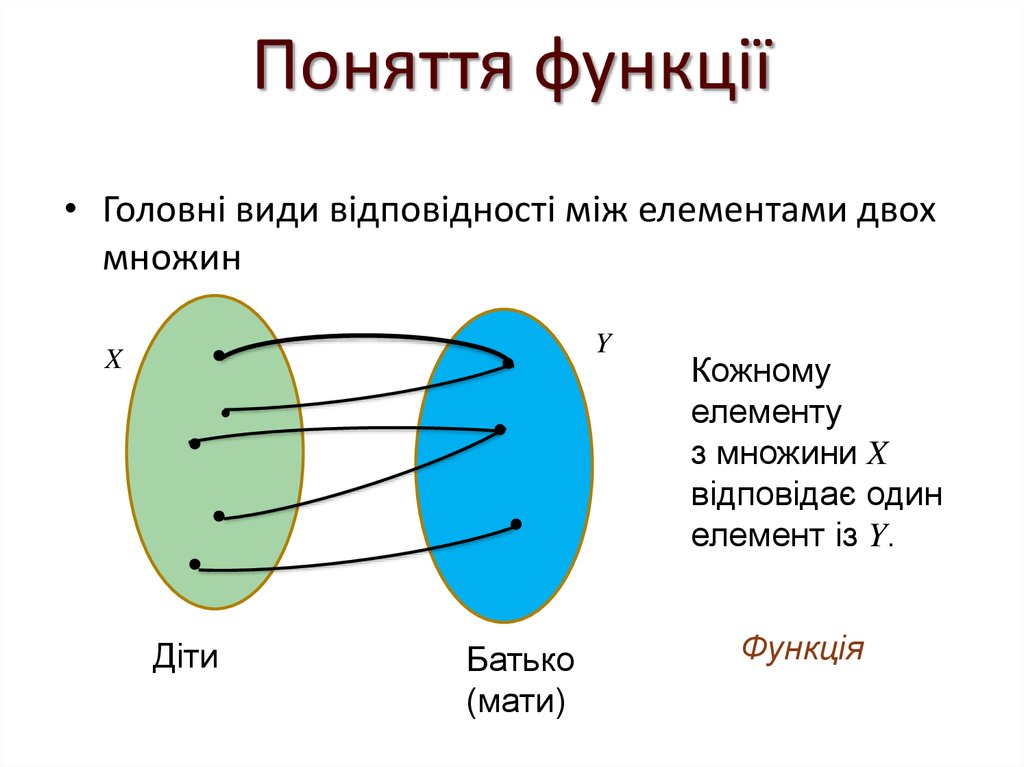
• Головні види відповідності між елементами двохмножин
Ін’єкція
Y
X
Діти
Батько
(мати)
Кожному
елементу
з множини X
відповідає один
елемент із Y.
Функція
13. Поняття функції
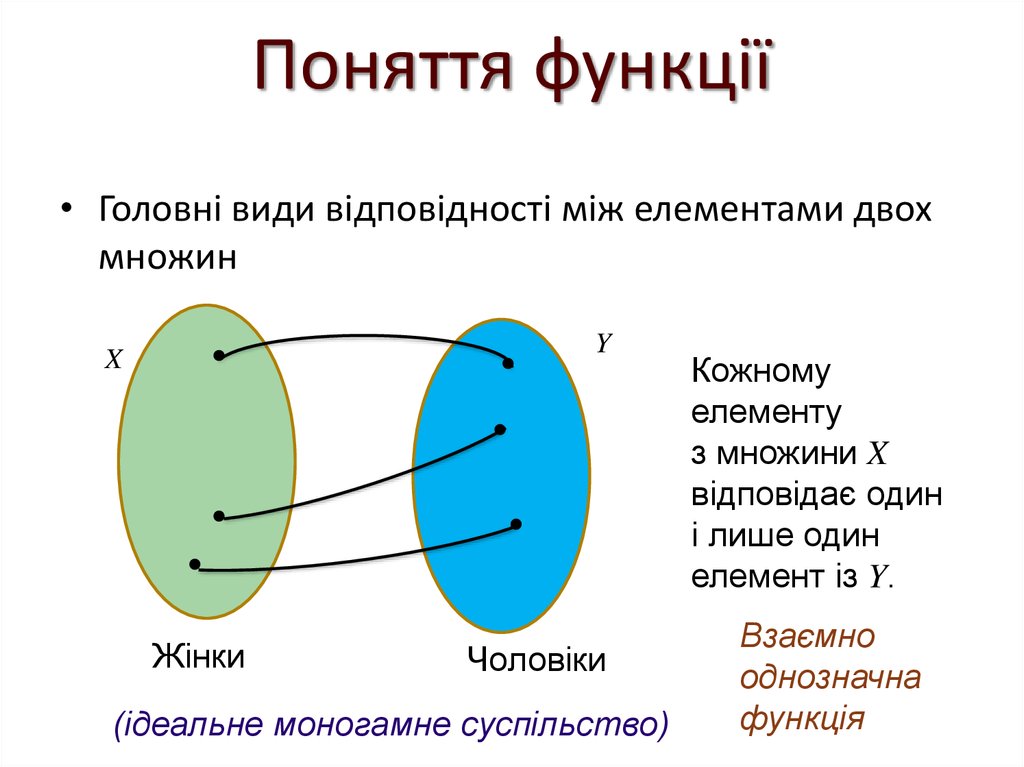
• Головні види відповідності між елементами двохмножин
Бієкція
Y
X
Жінки
Чоловіки
(ідеальне моногамне суспільство)
Кожному
елементу
з множини X
відповідає один
і лише один
елемент із Y.
Взаємно
однозначна
функція
14. Поняття функції
4• Відношення
3
x 2 y 2 9;
2
X x 3 x 3 ;
Y y 3 y 3 .
1
0
-4
-2
-1
-2
-3
-4
0
2
4
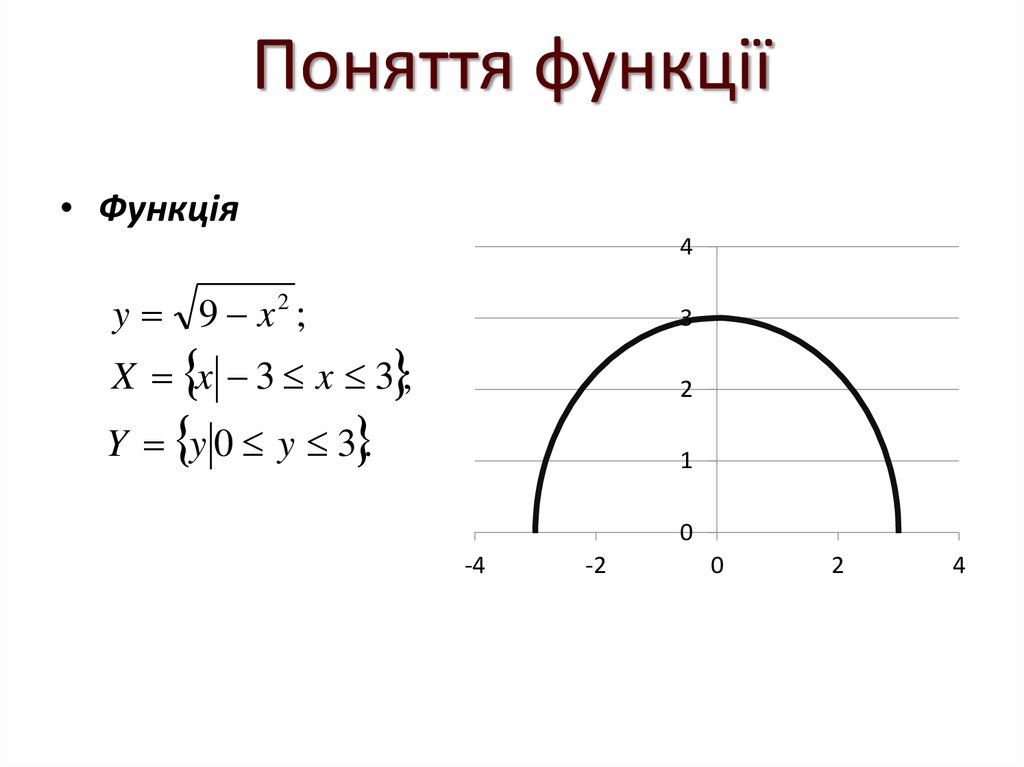
15. Поняття функції
• Функція4
y 9 x2 ;
3
X x 3 x 3 ;
2
Y y 0 y 3 .
1
0
-4
-2
0
2
4
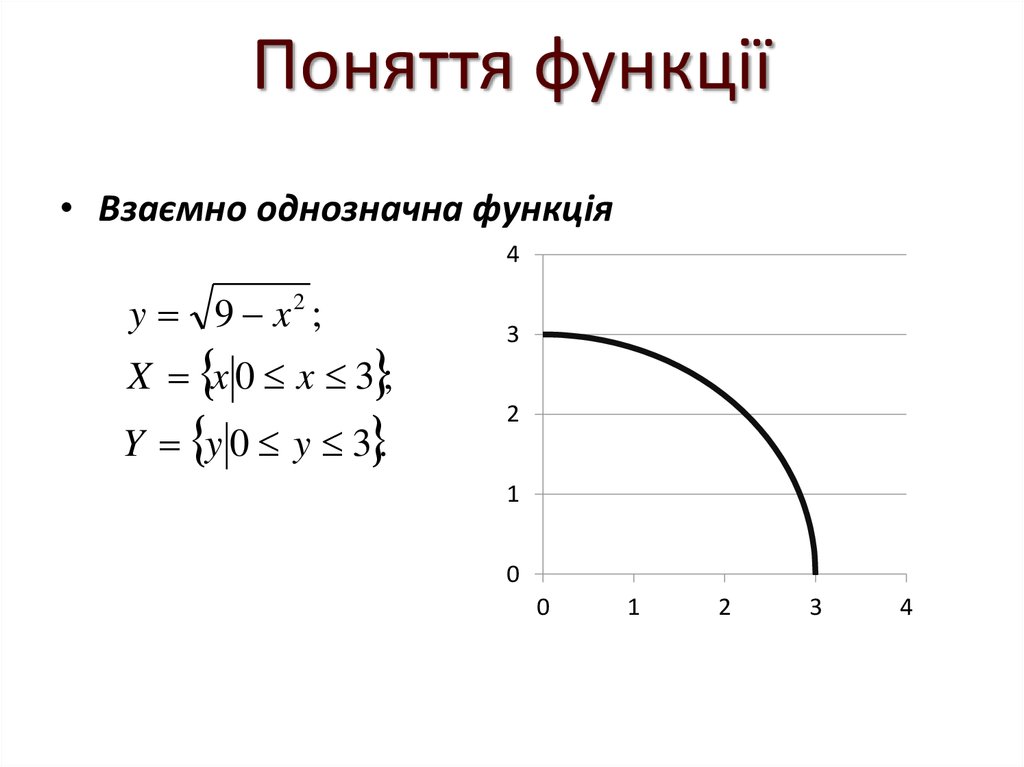
16. Поняття функції
• Взаємно однозначна функція4
y 9 x2 ;
X x 0 x 3 ;
Y y 0 y 3 .
3
2
1
0
0
1
2
3
4
17. Поняття функції
• Термін «функція» вперше ввів Г. Лейбніц.Озн. Функцією називається відповідність, при
якій кожному елементу х із множини D
відповідає деякий елемент y із множини E.
D – область визначення функції (позн. D(f));
Е – область значень функції (позн. E(f)).
Якщо D(f) і E(f) – числові множини, то функція
називається числовою.
18. Поняття функції
Озн. Числовою функцією з областювизначення D називається відповідність,
при якій кожному числу х D відповідає
деяке число y.
Озн. (М. Лобачевського і Л.Діріхле)
Якщо кожному числу х з деякої числової
множини Х за певним правилом
поставлене у відповідність єдине число y,
то кажуть, що у є функцією від х.
19. Поняття функції
y x,y Arcsin x.
X Y;
f : X Y;
y f ( x ).
f : x y;
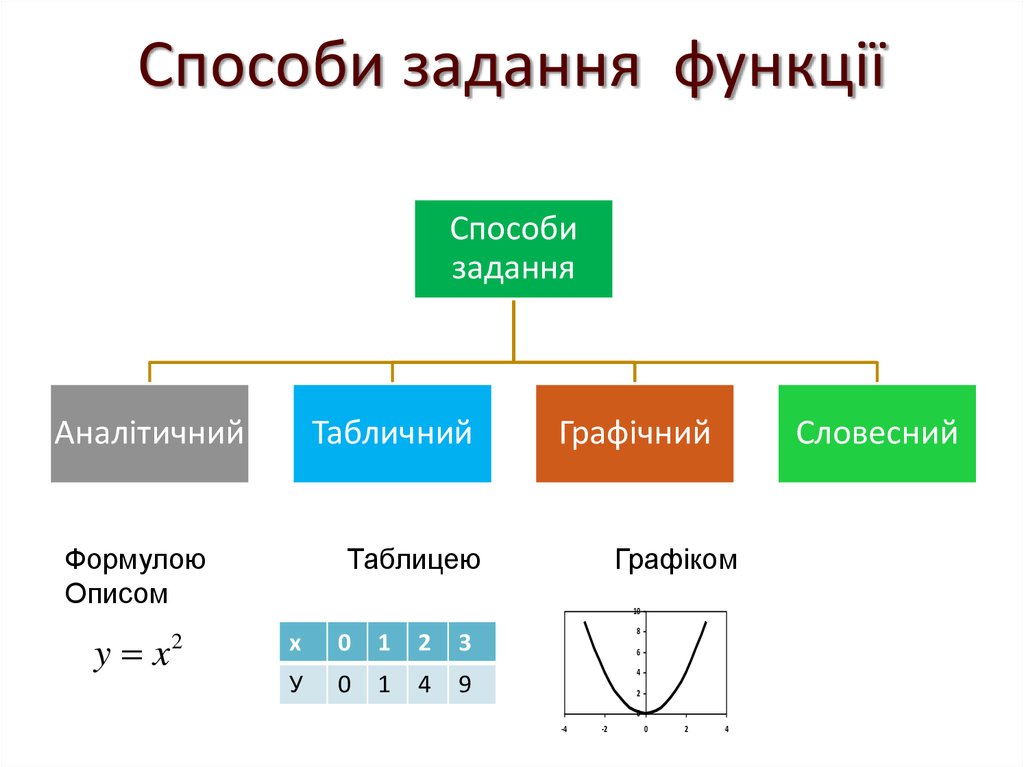
20. Способи задання функції
Способизадання
Аналітичний
Табличний
Формулою
Описом
y x
2
Графічний
Таблицею
Словесний
Графіком
10
х
0
1
2
3
У
0
1
4
9
8
6
4
2
0
-4
-2
0
2
4
21. Способи задання функції
y x , x [0,1];2
y x , x [2,4].
2
2 x 1, x 0;
y
ln x 1, x 0.
22. Властивості функцій
• Озн. Функцію y = f(x), визначену намножині Х, називають обмеженою на цій
множині, коли існує таке число М > 0,
що для всіх х Х виконується нерівність
| f(x)|≤ М.
23. Властивості функцій
• Озн. Функція y = f(x) називаєтьсямонотонно зростаючою,
строго зростаючою,
монотонно спадною,
строго спадною,
x1, x2 X ( x1 x2 )
якщо для кожної пари
виконується нерівність:
f(x1) ≤ f(x2).
f(x1) < f(x2).
f(x1) ≥ f(x2).
f(x1) > f(x2).
24. Властивості функцій
• Озн. Функція y = f(x) називаєтьсяпарною,
непарною,
загального вигляду (ні парна, ні непарна),
якщо для кожного x X виконується:
f(–x) = f(x).
f(–x) = – f(x).
не виконується жодна умова.
(область визначення симетрична відносно точки 0)!
25. Властивості функцій
• Озн. Функція y = f(x), визначена на всій числовійпрямій, називається періодичною,
якщо існує таке число Т ≠ 0, що f(x + Т) = f(x).
• Озн. Функція y = f(x), визначена множині Х,
називається періодичною на цій множині,
якщо існує таке число Т ≠ 0, що х + Т Х і
f(x + Т) = f(x).
26. Властивості функцій
• Озн. Під неявним заданням функціїрозуміють задання функції у вигляді
рівняння F ( x, y ) 0, нерозв’язаного
відносно залежної змінної.
27. Властивості функцій
• Озн. Функція x ( y ) є оберненою до функції,якщо: y f (x )
• 1) областю визначення функції є множина
значень функції f;
• 2) множина значень функції є область
визначення функції f;
• 3) кожному значенню змінної y Y відповідає
єдине значення змінної x X.
28. Властивості функцій
• Озн. Задання функціональної залежностіміж х і y у вигляді двох функцій
x (t ), y (t )
називають параметричним заданням
функцій.
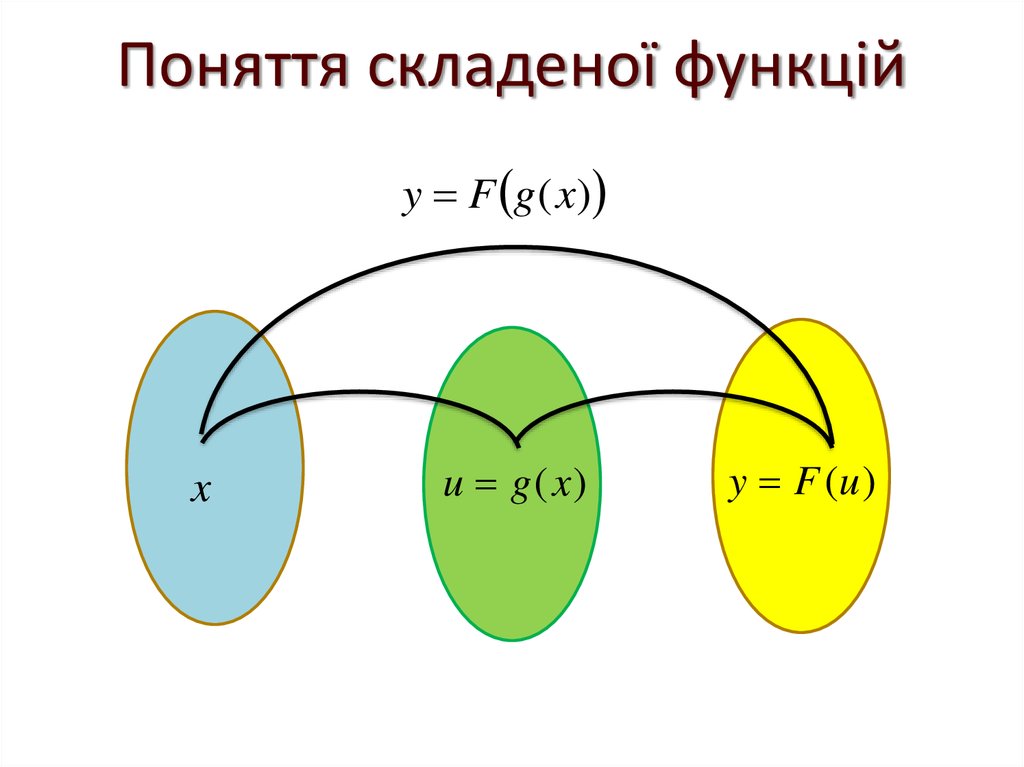
29. Поняття складеної функцій
y F g (x)x
u g (x )
y F (u )
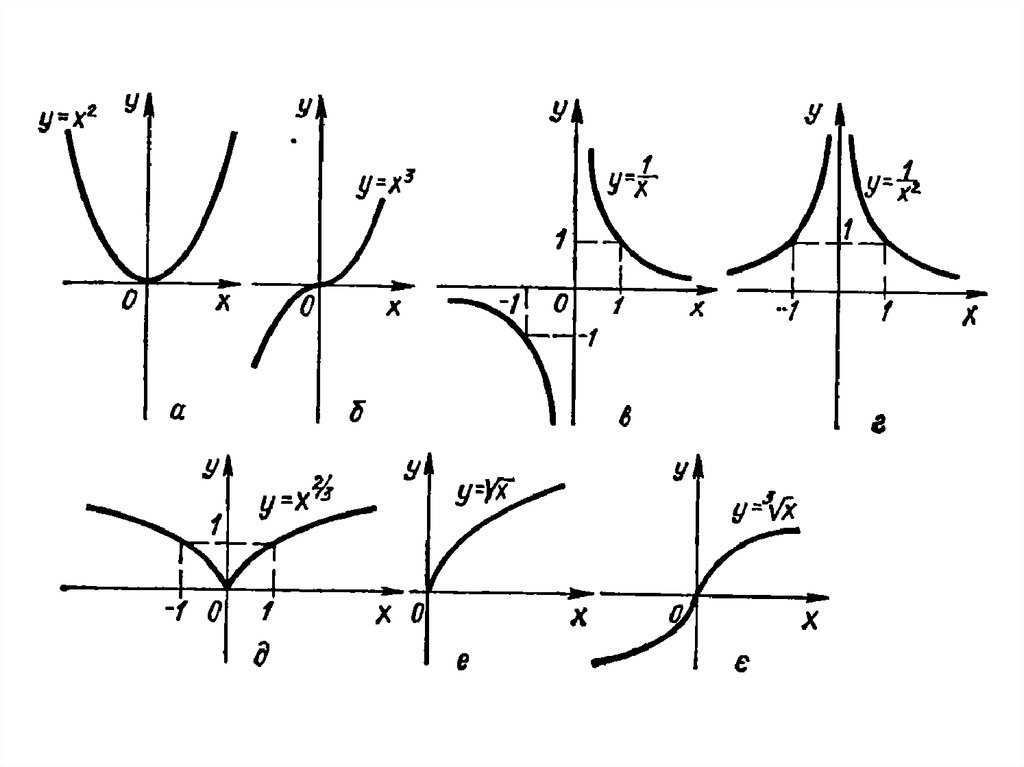
30. Елементарні функції
• Озн. Основними елементарними функціяминазиваються такі:
• 1. Лінійна функція y ax b, a, b R;
• 2. Степенева функція y x , R;
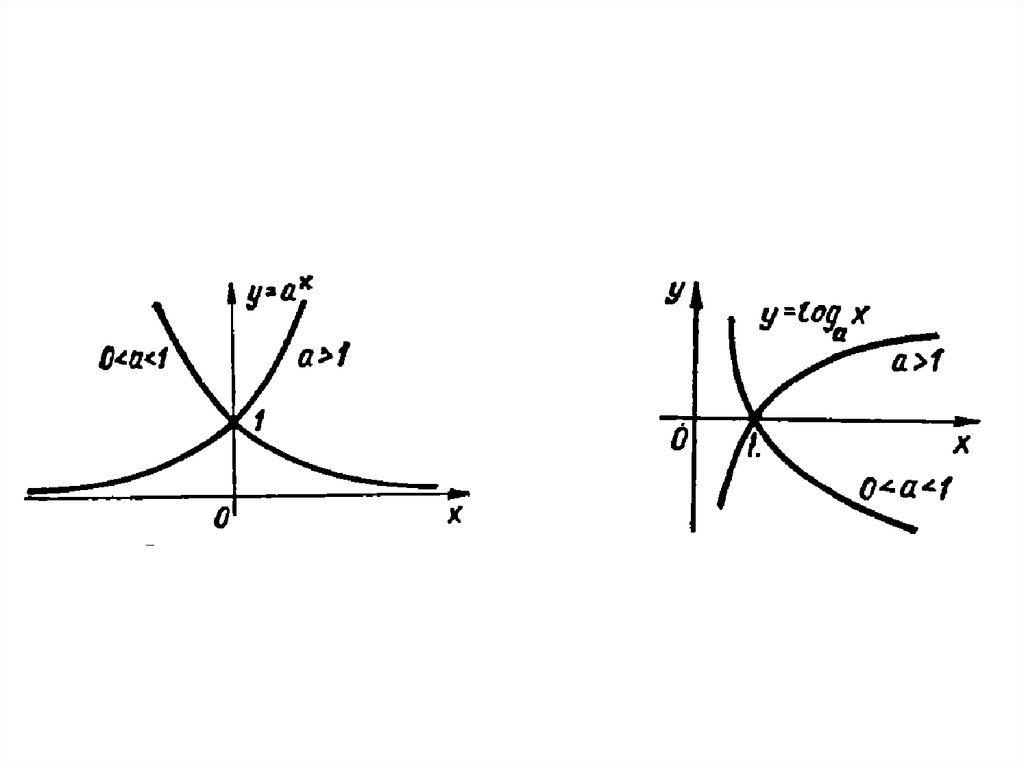
x
y a , a 0, a 1;
• 3. Показникова функція
• 4. Логарифмічна функція y log a x, a 0, a 1;
y sin x, y tg x;
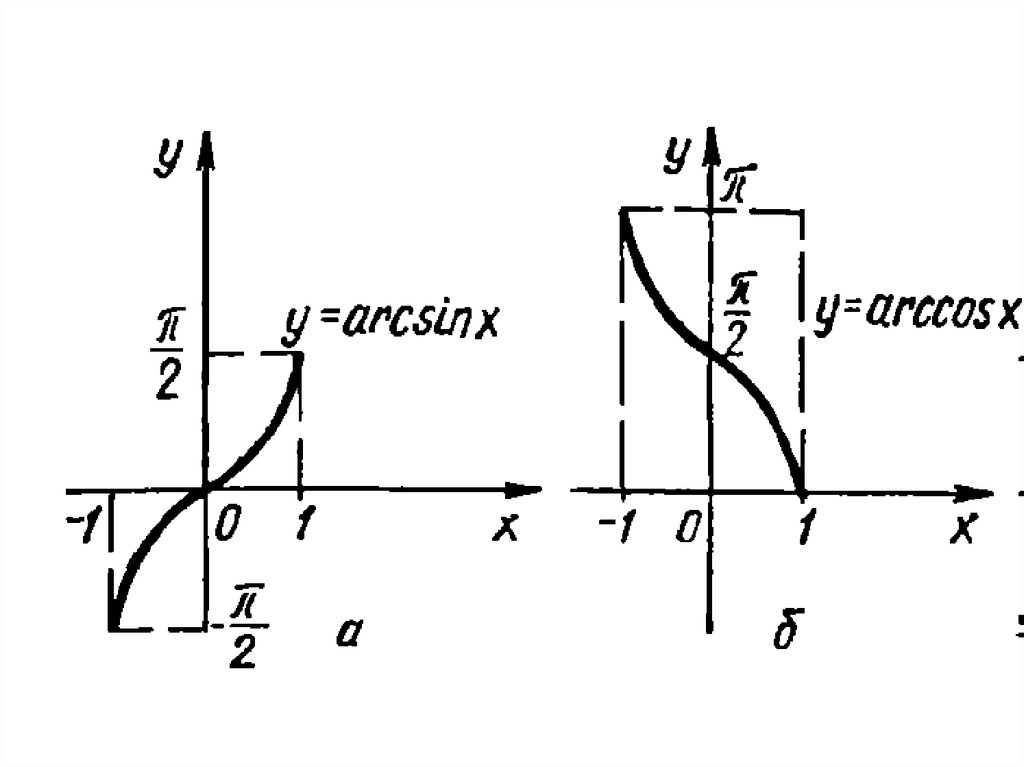
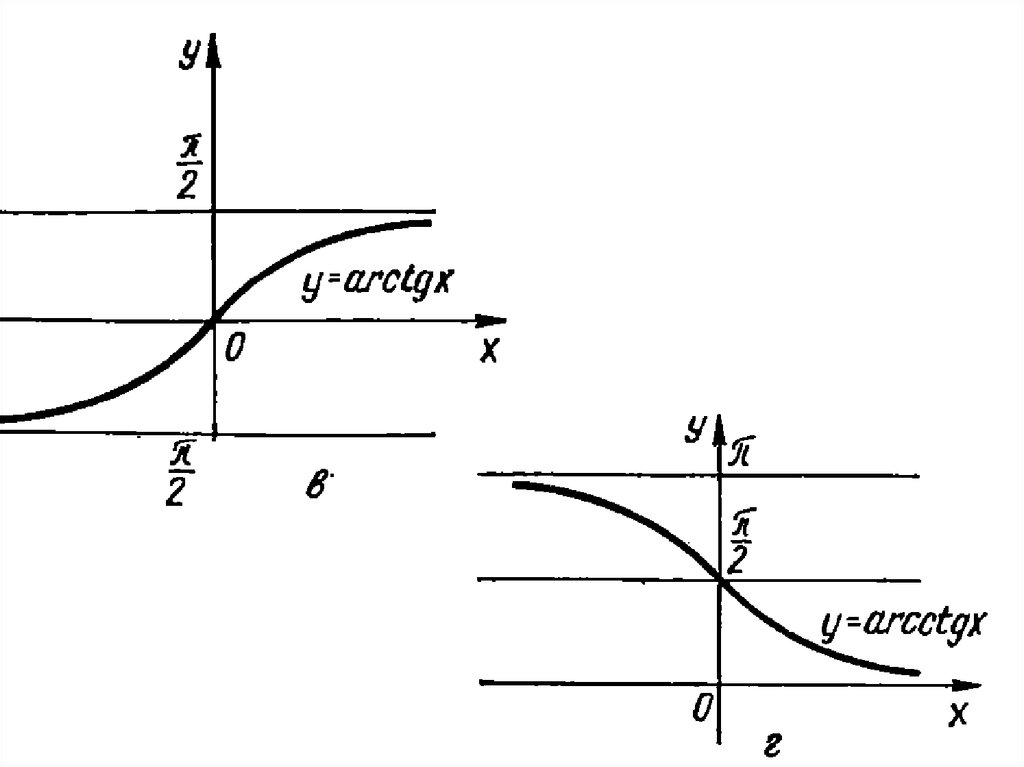
• 5. Тригонометричні функції
y arcsin x;
• 6. Обернені тригонометричні функції
• інші.
• (Гіперболічні функції
y sh x, y th x. )
31.
32.
33.
34.
35.
36. §3. Границя функції
• 3.1. Числова послідовністьa1 , a2 ,...an ...
b1 , b2 ,...bn ...
an a1 d (n 1)
bn b1 q
n 1
Sn
a1 an n
bn q b1
Sn
q 1
q 1
2
b1
S
1 q
q 1
37.
3.1. Числова послідовністьЯкщо кожному натуральному числу п ℕ
за певним правилом ставиться у відповідність
число хп, то множину чисел
x1, x2 , ... xn ...
називають числовою послідовністю (або коротко
послідовністю) і позначають символом {хn}.
xn
xn 2 n 2 1
yn
yn cos n 1
yn f (n)
an
an an 1 an 2
a1 1 a2 1
38.
1xn
n
1
1 1 1
,...
1, , , ,...,
100
2 3 4
• 3.2. Границя числової послідовності.
Єдиність границі
Число х0 називається границею послідовності {хn},
якщо
для довільного числа ε > 0
існує такий номер N = N (ε),
що при всіх п > N виконується нерівність
xn x0 .
lim xn x0
n
xn x0
39.
3.2. Границя числової послідовності. Єдиність границі0 N N ( ) : n N xn x0 .
Послідовність, яка має границю, називається
збіжною. Послідовність, яка не є збіжною,
називається розбіжною.
xn
x0
x0
x0
x
40.
• 3.4. Границя функції в точціЧисло А називають границею функції у = f (х) в точці
х0, якщо для довільної збіжної до х0 послідовності
{хn}, де хn X, хn х0, послідовність
{f (хn)} має границю, яка дорівнює числу А, і
записують
lim f ( x) A.
x x0
41.
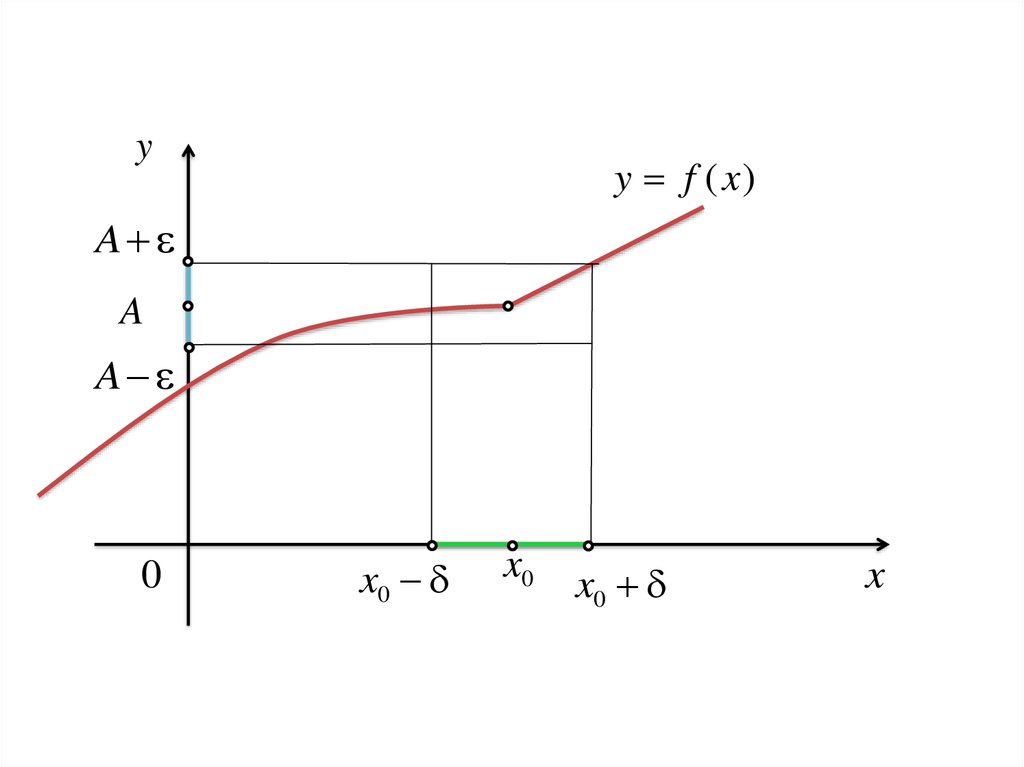
Число А називають границею функції в точці х0,якщо
для довільного числа ε > 0
існує число δ = δ (ε) > 0,
що при всіх х X, які задовольняють нерівність
0 x x0 ,
виконується нерівність
f ( x) A .
0 ( ) : 0 x x0 f ( x) A .
42.
yy f (x )
A
A
A
0
x0
x0
x0
x
43.
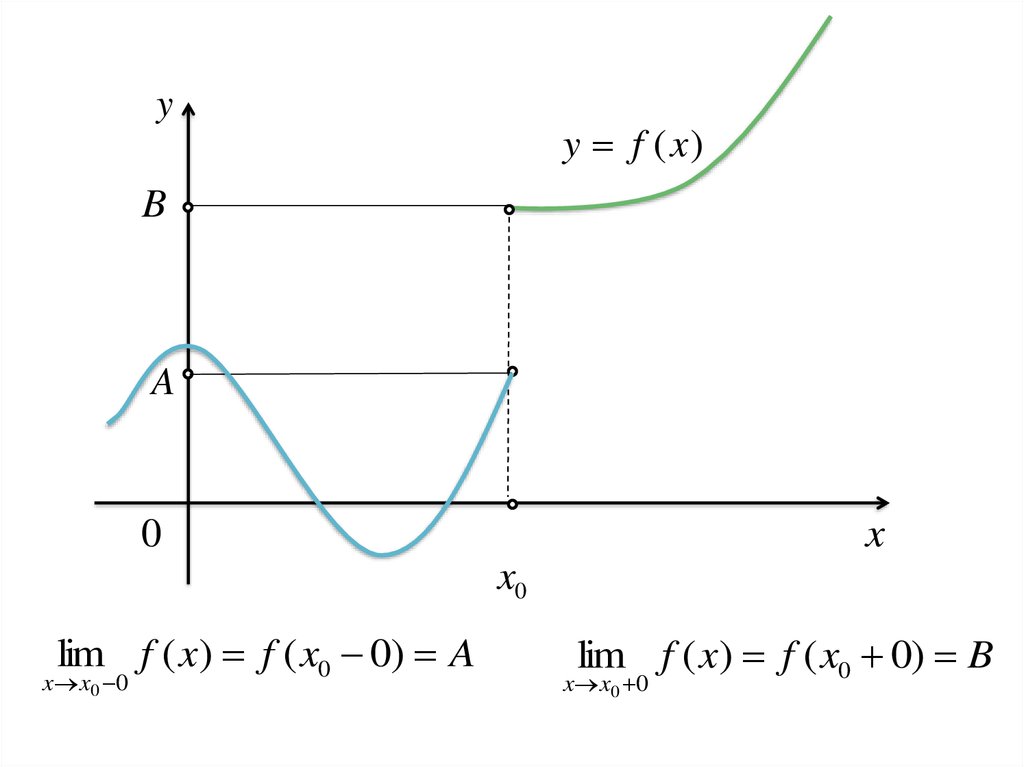
yy f ( x)
B
A
x
0
x0
lim f ( x) f ( x0 0) A
x x0 0
lim f ( x) f ( x0 0) B
x x0 0
44.
ПрикладДовести, що
lim 3x 2 5
x 1
0 ( ) : 0 x x0 f ( x) A .
f ( x) A
3x 2 5
3x 3
x 1
3
0 x x0
x 1
3
45.
ПрикладДовести, що
2x 5
lim
2.
x
x
0 M M ( ) :
x M f ( x) A .
f ( x) A
2x 5
2
x
5
2 2
x
5
x
5
x M
46.
Функцію f (х), задану на всій числовій прямій,при х →x0 називають нескінченно великою і пишуть
lim f ( x)
x x0
M 0 ( M ) 0 : 0 x x0 f ( x) M .
Нескінченно малою величиною називається
змінна величина, границя якої дорівнює нулю.
lim ( x) 0
x x0
lim ( x ) 0
x
47.
Функцію f (х), задану на всій числовій прямій,при х →∞ називають нескінченно великою і пишуть
lim f ( x )
x
M 0 N N ( M ) 0 :
x N f ( x) M .
48.
• 3.7. Основні теореми про границіТеорема 1 (про границю суми, добутку і частки).
Якщо кожна з функцій f(х) та φ(х) має скінченну
границю в точці х0, то в цій точці існують також
границі функцій суми, різниці, добутку та частки,
(остання за умови, що знаменник відмінний від
нуля) і справедливі формули
lim f ( x) ( x) lim f ( x) lim ( x);
x x0
x x0
x x0
lim f ( x) ( x) lim f ( x) lim ( x);
x x0
x x0
f ( x)
f ( x ) xlim
x0
lim
.
x x0 ( x )
( x )
xlim
x
0
x x0
49.
ПрикладОбчислити
lim 5x 13x 5 .
2
x 2
lim 5x 2 13x 5 5 lim x 2 13 lim x lim 5
x 2
x 2
x 2
5 22 13 2 5 20 26 5 1.
x 2
50.
ПрикладОбчислити
x 2 5x 6
lim
.
2
x 3
x 9
x 3 x 2
x 2 5x 6 0
lim
lim
2
x 3 x 3 x 3
x 3
x 9
0
x 2
lim
x 3 x 3
3 2 1
.
3 3 6
51.
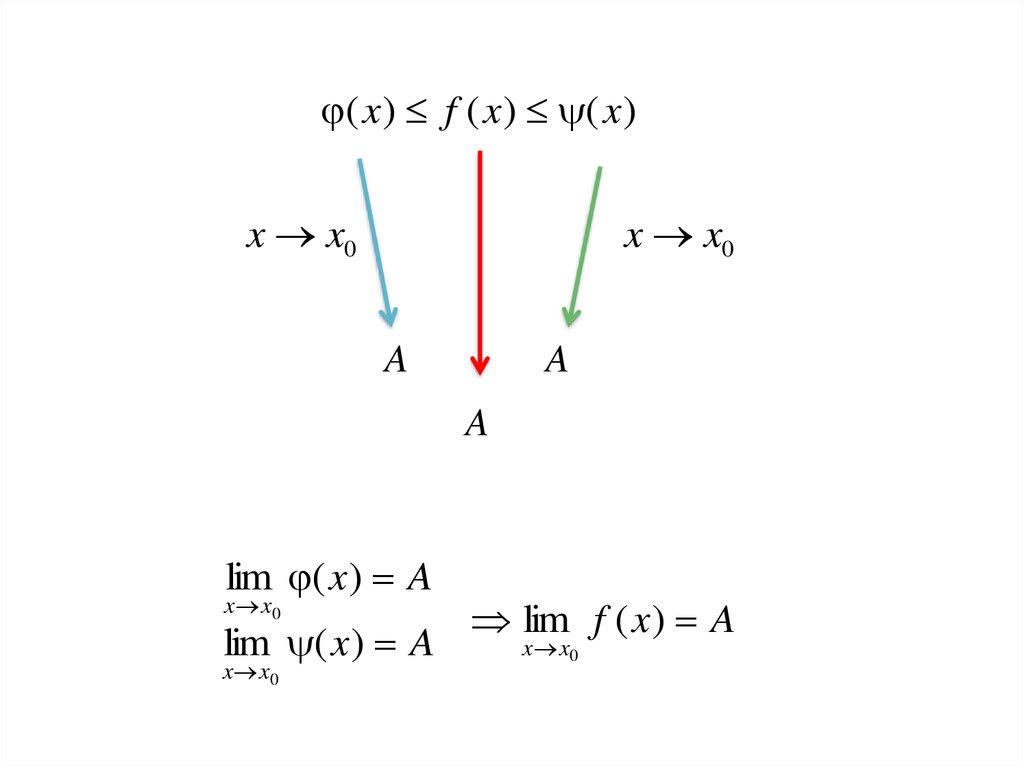
( x ) f ( x ) ( x )x x0
x x0
A
A
A
lim ( x ) A
x x0
lim ( x ) A
x x0
lim f ( x ) A
x x0
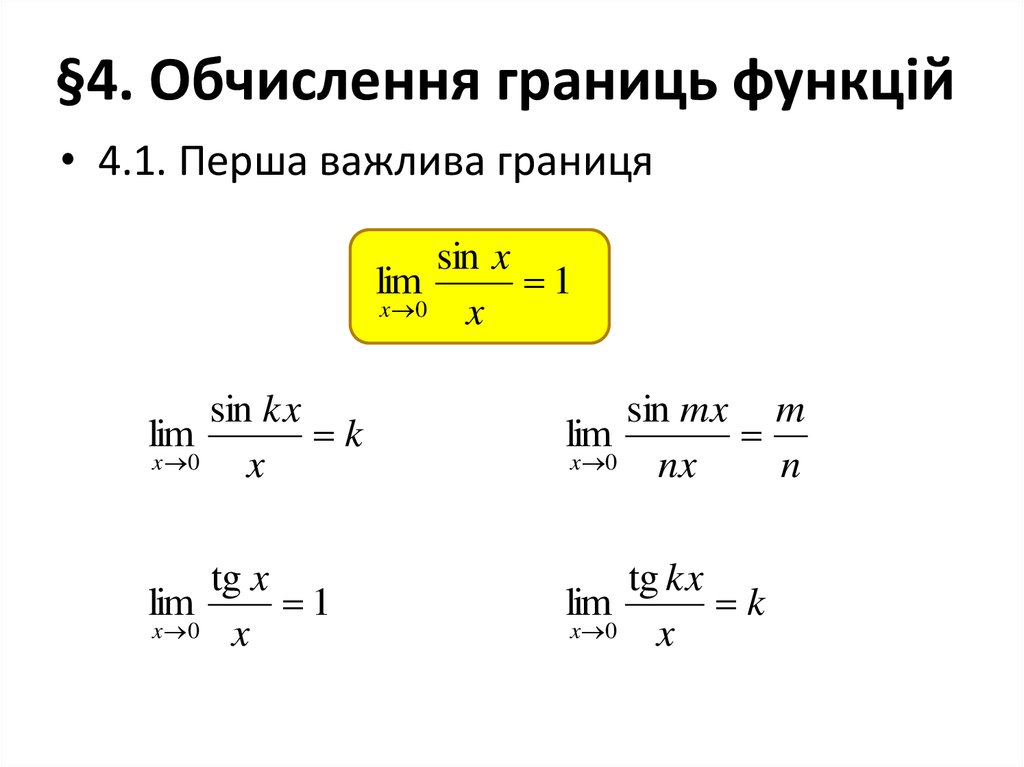
52. §4. Обчислення границь функцій
• 4.1. Перша важлива границяsin x
lim
1
x 0
x
sin kx
lim
k
x 0
x
sin mx m
lim
x 0
nx
n
tg x
lim
1
x 0 x
tg kx
lim
k
x 0
x
53.
Прикладcos 5 x cos 3x
lim
x 0
x2
2 sin 4 x sin( x )
lim
2
x 0
x
sin 4 x
sin( x )
2 lim
lim
2 4 1 8.
x 0
x x 0
x
54.
• 4.3. Друга важлива границяx
1
lim 1 e
x
x
1
x
lim 1 x e
x 0
1
nx
k
lim 1 e kn
x
x
e 2,71828
log e a ln a
e x exp( x )
55.
Приклад1 5 x
2x 1
lim
x 2 x 3
1
1 5 x
4
lim 1
x
2x 3
lim e
x
4
1 5 x
2 x 3
1 5 x
2x 3 3 1
lim
x
2x 3
4
lim 1
x
2x 3
lim e
x
20 x 4
2 x 3
10
e
.
2 x 3 4
1 5 x
4 2 x 3
56.
0sin ~
tg ~
e 1 ~
a 1 ~ ln a
arcsin ~
arctg ~
2
1 cos ~
2
ln( 1 ) ~
(1 )k 1 ~ k
57.
Приклад2
1
1 3 4
x4 2 x 1
1
x
x
lim
.
lim 4
2
x 3x x 10 x 5
3
x 3 1 10 5
x2 x3 x4
x 2 x x x 2 x x
lim
x 2x x
lim
x
x
2
2 x x
2
x
lim
x
2
2
2
1.
2
1 1
x
lim
x
2x
x2 2 x x
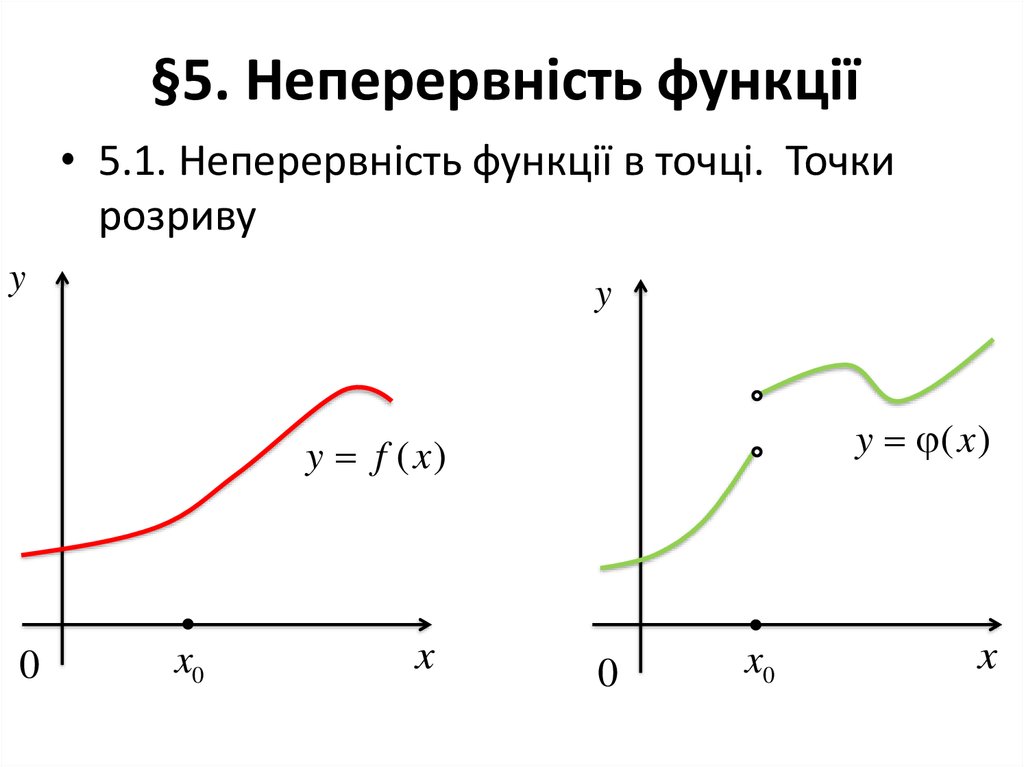
58. §5. Неперервність функції
• 5.1. Неперервність функції в точці. Точкирозриву
y
y
y (x )
y f (x )
0
x0
x
0
x0
x
59.
Озн. Функція f(х) називається неперервною в точці х0,якщо границя функції і її значення в цій точці рівні, тобто
lim f ( x) f ( x0 )
x x0
(23)
1. Функція визначена в точці х0 і в деякому околі цієї точки;
2. Існує границя lim f ( x );
x x0
3. Границя функції f(х) в точці х0 і значення функції в цій
точці х0 збігаються, тобто виконується рівність (23).
60.
lim f ( x) f ( x0 )x x0
f ( x) f ( x0 ) 0
x x 0
lim
0
lim f ( x ) 0
x 0
61.
lim f ( x) f ( x0 )x x0 0
lim f ( x) f ( x0 )
x x0 0
lim f ( x) lim f ( x) f ( x0 )
x x0 0
lim f ( x) f ( x0 0)
x x0 0
x x0 0
(26)
lim f ( x) f ( x0 0)
x x0 0
62.
Озн. Якщо для функції f(х)існують скінченні границі
Розрив першого роду
lim f ( x) f ( x0 0)
x x0 0
y
lim f ( x) f ( x0 0)
y f (x )
f ( x0 )
f ( x0 0)
f ( x0 0)
0
x x0 0
причому не всі числа
f ( x0 0),
x0
– стрибок
x
f ( x0 0),
рівні між собою,
то розрив в точці х0
називають розривом
першого роду,
точку х0 — точкою
розриву першого роду.
f ( x0 )
63.
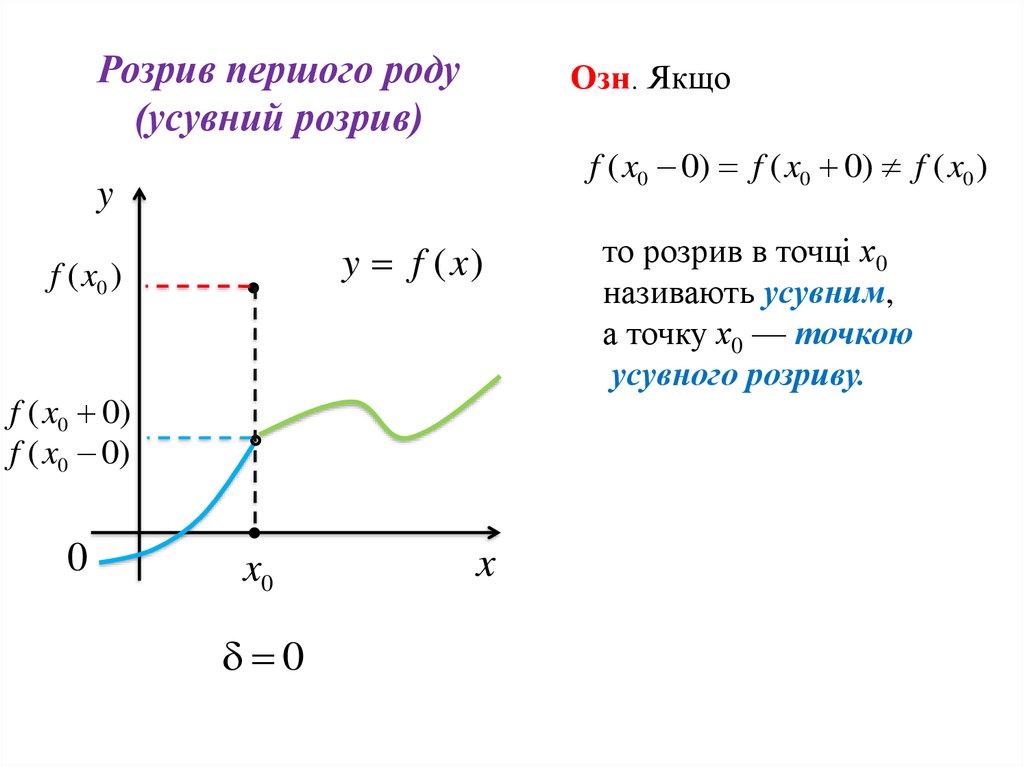
Розрив першого роду(усувний розрив)
Озн. Якщо
f ( x0 0) f ( x0 0) f ( x0 )
y
y f (x )
f ( x0 )
f ( x0 0)
f ( x0 0)
0
x0
0
x
то розрив в точці х0
називають усувним,
а точку х0 — точкою
усувного розриву.
64.
Розрив другого родуОзн. Якщо хоча б одна
з односторонніх границь
у формулі (26) не існує або
дорівнює нескінченності,
то розрив в точці х0
називається розривом
другого роду,
а сама точка х0 — точкою
розриву другого роду.
y
y f (x )
0
x0
x
65.
• 5.2. Дії над неперервними функціями.Неперервність елементарних функцій
Теорема. Якщо функції f(х) і φ(х) неперервні в точці х0 , то в
цій точці неперервними є функції
f ( x ) ( x ),
f ( x ) ( x ),
f ( x)
.
( x )
Теорема. Всяка елементарна функція неперервна в кожній
точці, в якій вона визначена.
66.
• 5.3. Властивості функцій, неперервних навідрізку
Озн. Якщо функція неперервна в кожній точці інтервалу (a; b),
то вона називається неперервною на цьому інтервалі.
Теорема. (перша теорема Больцано-Коші). Якщо функція
f(х) неперервна на відрізку [a; b] і на його кінцях набирає
значень різних знаків, то всередині відрізка [a; b] знайдеться
хоча б одна точка х = с, в якій функція дорівнює, нулю: f(с) = 0,
a < с < b.
y
y f (x )
a
0
b
c
x
67.
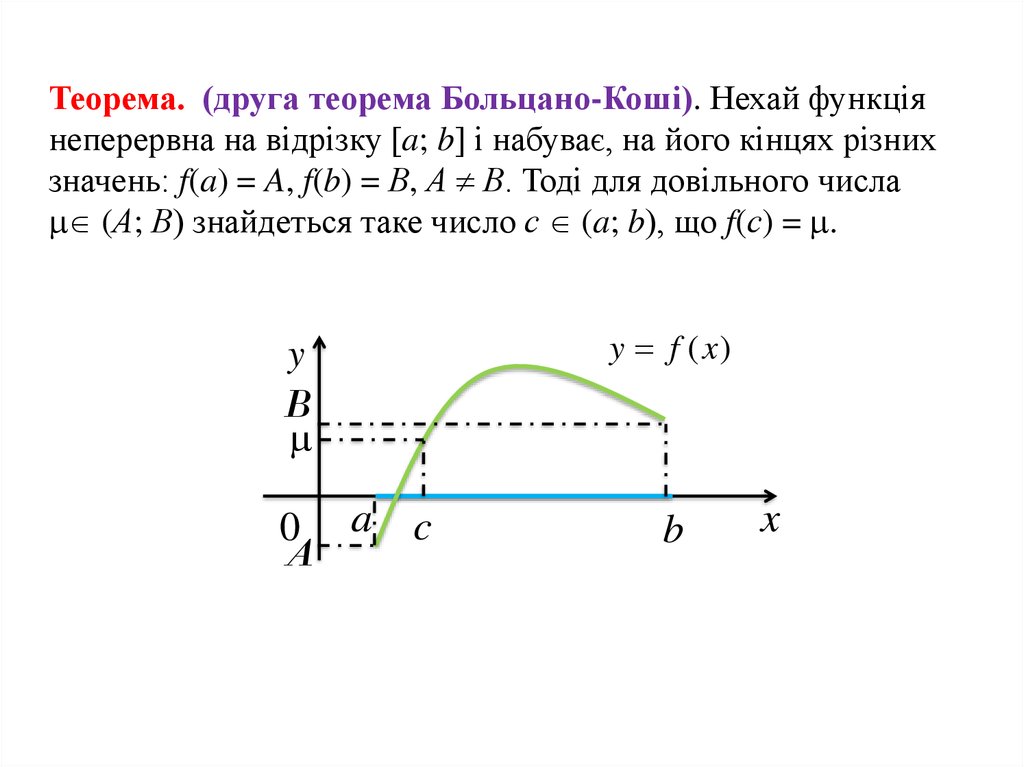
Теорема. (друга теорема Больцано-Коші). Нехай функціянеперервна на відрізку [a; b] і набуває, на його кінцях різних
значень: f(a) = A, f(b) = В, А В. Тоді для довільного числа
(А; В) знайдеться таке число с (a; b), що f(с) = .
y f (x )
y
B
0 a
A
c
b
x
68.
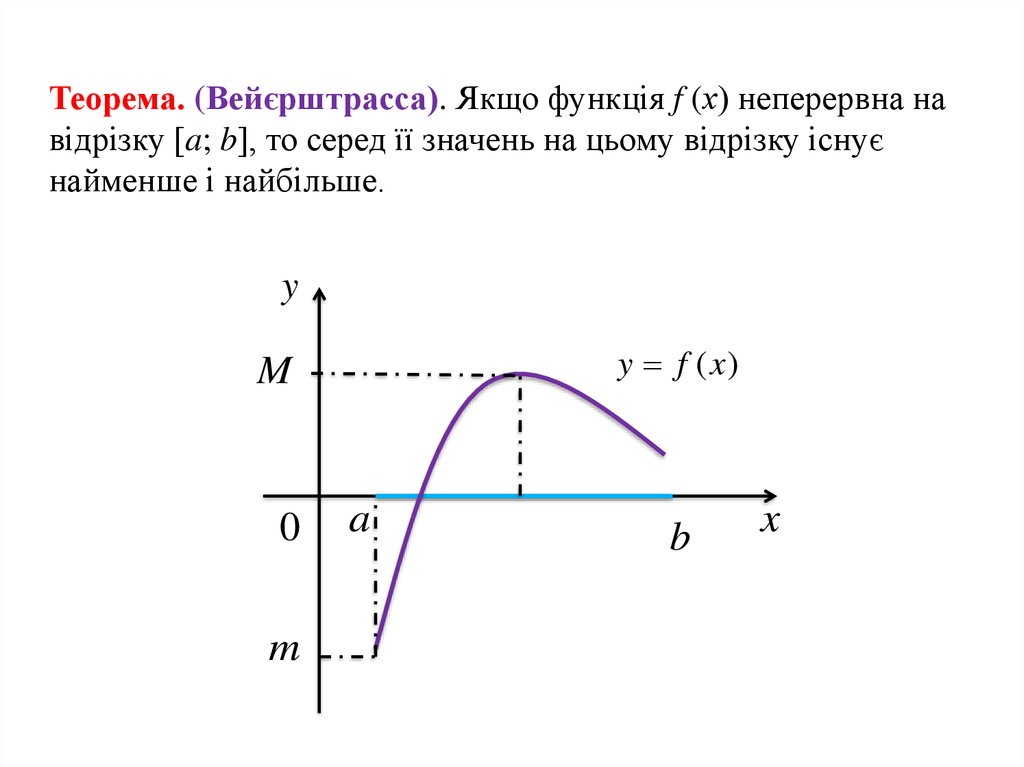
Теорема. (Вейєрштрасса). Якщо функція f (х) неперервна навідрізку [a; b], то серед її значень на цьому відрізку існує
найменше і найбільше.
y
y f (x )
M
0
m
a
b
x
69. §1. Похідна
Глава 5Диференціальне числення
функцій однієї змінної
§1. Похідна
• 1.1. Задачі, які приводять до поняття похідної
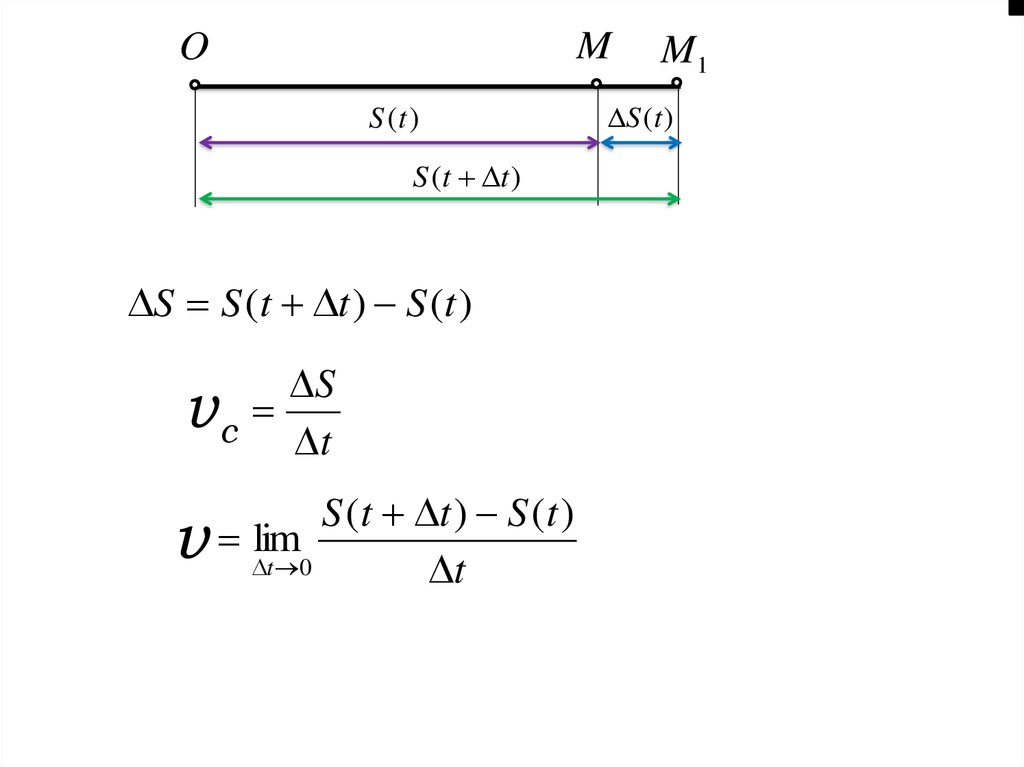
Задача про швидкість прямолінійного руху
M
O
S (t )
S (t t )
M1
S (t )
70.
MO
S (t )
S (t t )
S S (t t ) S (t )
S
v c t
S ( t t ) S ( t )
v lim
t 0
t
M1
S (t )
71.
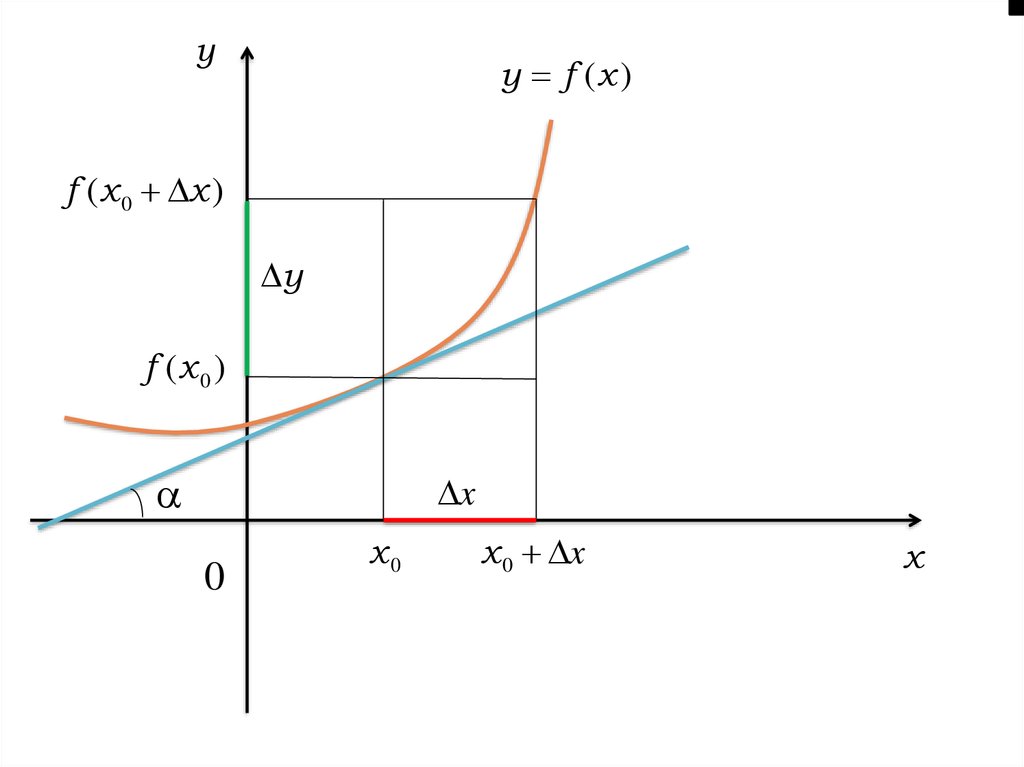
• 1.2. Означення похідної. Механічний, фізичний тагеометричний зміст похідної
Озн. Похідною функції у = f (х) в точці х називається
границя відношення приросту функції ∆у в цій точці до
приросту аргументу ∆х, коли приріст аргументу прямує
до нуля.
y
f ( x x ) f ( x )
f ( x ) lim
lim
.
x 0 x
x 0
x
y
dy
dx
f (x )
72.
ПрикладЗнайти похідну функцію
y x
2
y x x x 2 2 x x x 2
2
y 2 x x x 2
2 x x
x
x
y
lim
lim 2 x x 2 x
x 0 x
x 0
x 2 x
2
73.
yy f (x )
f (x 0 x )
y
f (x 0 )
x
0
x0
x 0 x
x
74.
Швидкість в даний момент часу — це похідна відпройденого шляху S(t) за часом t: v = S′(t).
Це механічний зміст похідної. Узагальнюючи, можна
сказати: якщо функція у = f (х) описує деякий фізичний
процес, то похідна у' = f' (х) є швидкістю зміни цього
процесу. В цьому полягає фізичний зміст похідної.
Кутовий коефіцієнт дотичної до кривої у = f (х) в точці
М0(х0; у0) або тангенс кута α, що утворює дотична до
кривої в даній точці з додатним напрямом осі Ох,— це
похідна f' (х0) в цій точці:
k = tg α = f' (х0).
У цьому полягає геометричний зміст похідної.
75.
yРівняння дотичної
y f (x )
y y0 f ( x0 ) x x0
Рівняння нормалі:
1
x x0
y y0
f ( x0 )
0
x0
x
76.
• 1.4. Односторонні похідні. Неперервність ідиференційовність
Права похідна
y
f ( x x ) f ( x )
f ( x ) lim
lim
.
x 0 x
x 0
x
x 0
x 0
Ліва похідна
y
f ( x x ) f ( x )
f ( x ) lim
lim
.
x 0 x
x 0
x
x 0
x 0
77.
Озн. Функція f (х) називається диференційовноюв точці х0, якщо в цій точці вона має похідну f '(х).
Озн. Функцію f (х) називають диференційовною
на проміжку, якщо вона диференційовна в кожній точці
цього проміжку.
Теорема. Якщо функція f (х) диференційовна в точці х0,
то вона в цій точці неперервна.
78. §2. Диференціювання функцій
Cu Cuu v
u v
uv u v uv
y f (u), u u( x) y x yu u x
1
y f ( x ), x ( y ) y x
x y
yt
y y (t ), x x (t ) y x
xt
u u v uv
v
v
v 1
u
u
ln
u
v
vu
u
2
v
v
uvw u vw uv w uvw
79.
1. C 02. u u 1u
u
3. a a u ln au
u
u
4. e e u
1
5. log a u
u
u ln a
1
6. ln u u
u
7. sin u cos u u
8. cos u sin u u
1
9. tg u
u
2
cos u
1
10. ctg u 2 u
sin u
11. sh u ch u u
12. chu sh u u
1
13. th u 2 u
ch u
1
14. cth u 2 u
sh u
1
15. arcsin u
u
1 u2
1
16. arccos u
u
2
1 u
1
17. arctg u
u
2
1 u
1
18. arcctg u
u
2
1 u
80.
1ln y y
y
y y ln y
Приклад
Знайти похідну функцію y x
1.
2.
3.
sin5 x
ln y ln x sin5 x sin 5x ln x
ln y sin 5x ln x
sin 5 x ln x sin 5 x ln x
1
5 cos 5 x ln x sin 5 x
x
y y ln y x sin5 x 5 cos 5 x ln x sin 5 x 1 .
x
81.
11
2;
x
x
x 2
1
x
.
e x e x
sh x
2
e x e x
ch x
2
e x e x
th x x x
e e
ch 2 x sh 2 x 1
sh 2 x 2 sh x ch x

























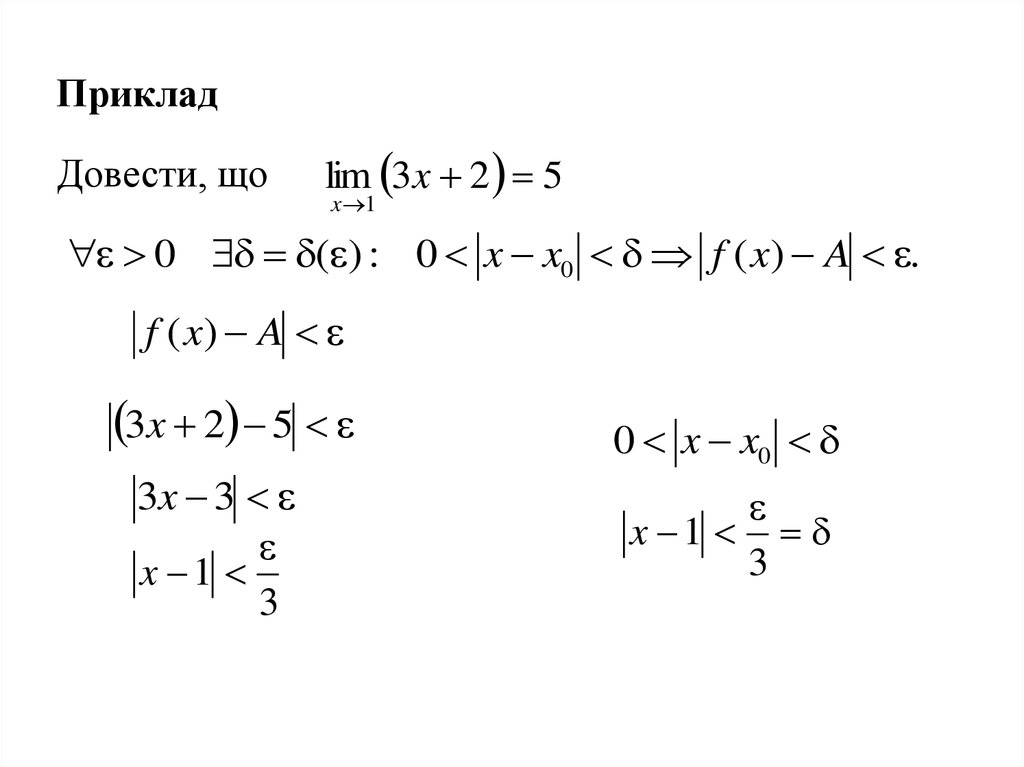













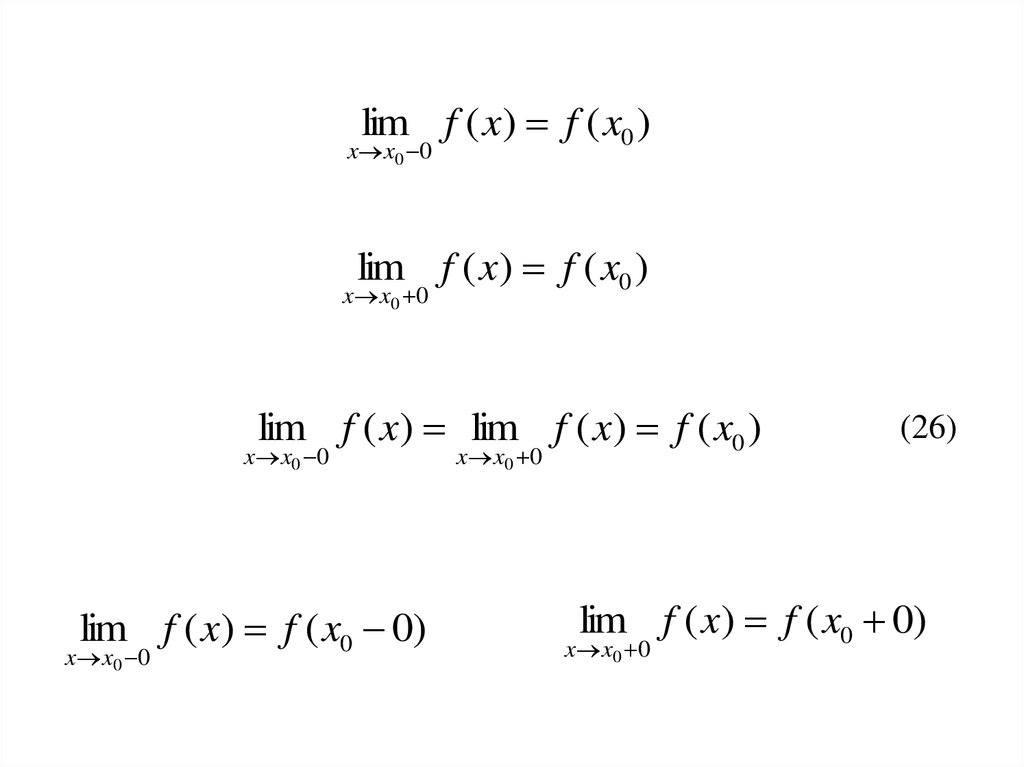














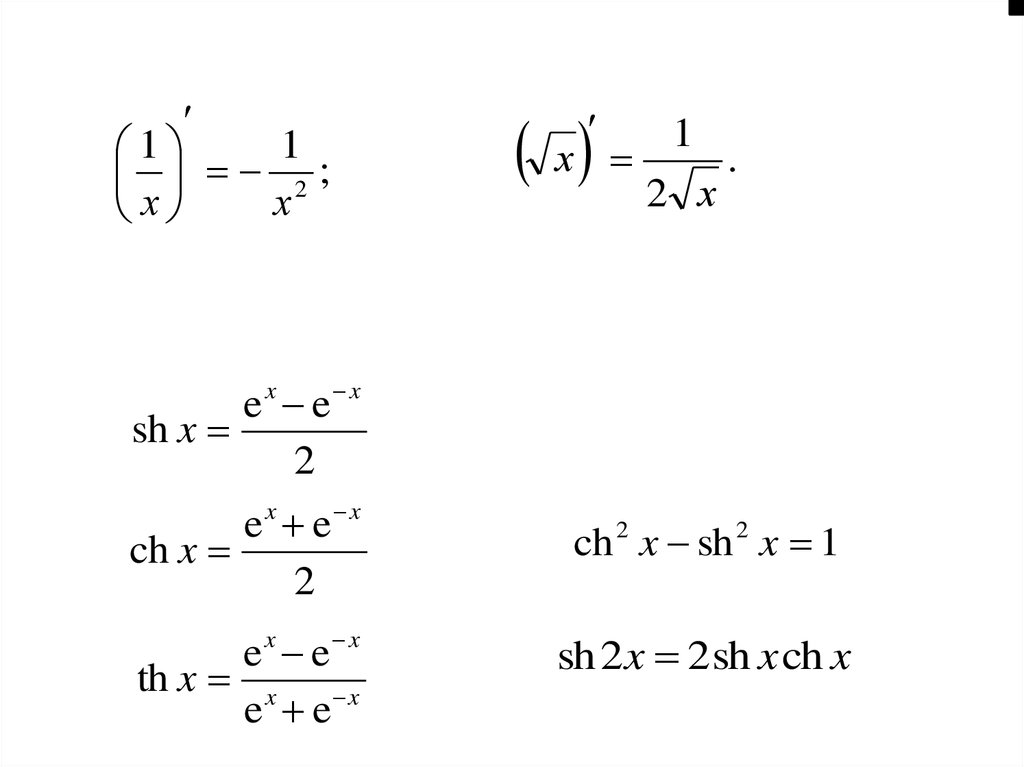

 mathematics
mathematics








