Similar presentations:
Класифікація елементарних функцій
1. Класифікація елементарних функцій
2. 1. Лінійна функція y=kx+b
Властивості:
1. D( y) R , E( y ) R
2. k>0 - зростає, k<0 - спадає.
3. Функція загального вигляду.
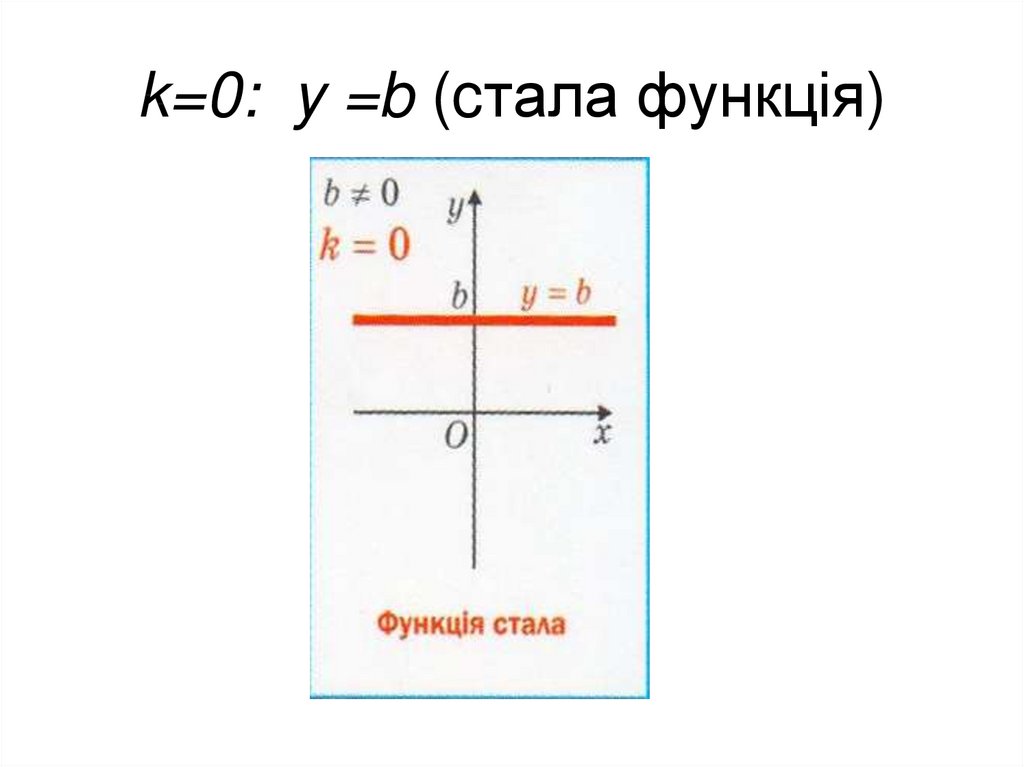
3. k=0: y =b (cтала функція)
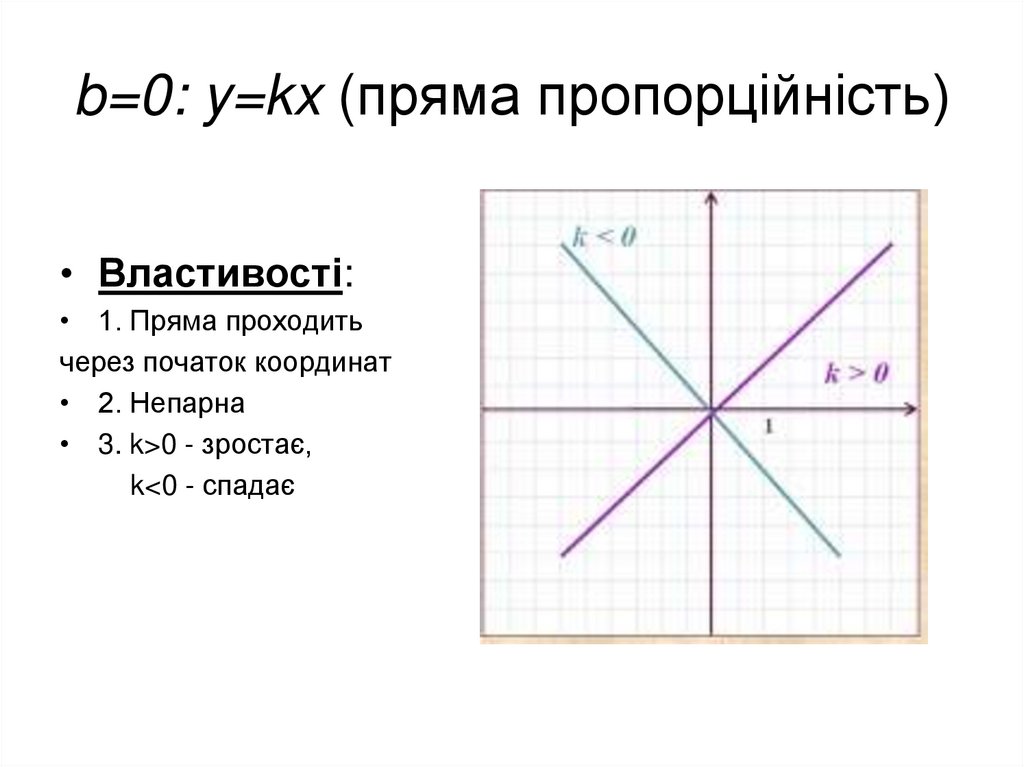
4. b=0: y=kx (пряма пропорційність)
• Властивості:• 1. Пряма проходить
через початок координат
• 2. Непарна
• 3. k>0 - зростає,
k<0 - спадає
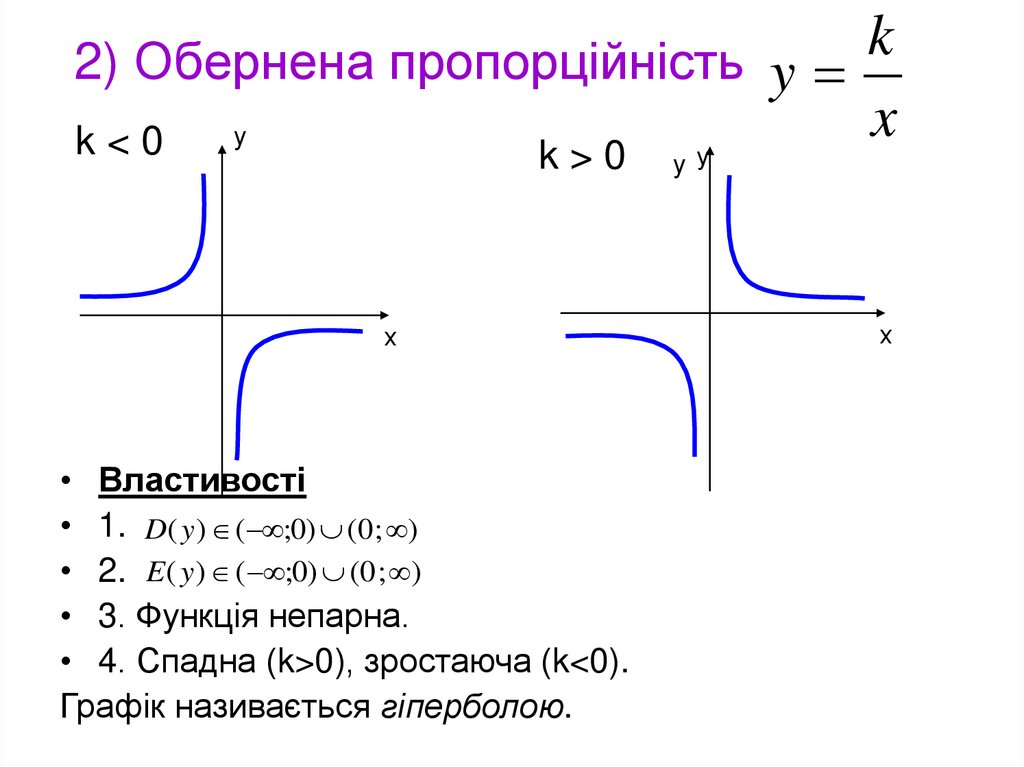
5. 2) Обернена пропорційність
k2) Обернена пропорційність y
x
y
k<0
k>0
х
• Властивості
• 1. D( y ) ( ;0) (0 ; )
• 2. E ( y ) ( ;0) (0 ; )
• 3. Функція непарна.
• 4. Спадна (k>0), зростаюча (k<0).
Графік називається гіперболою.
y у
х
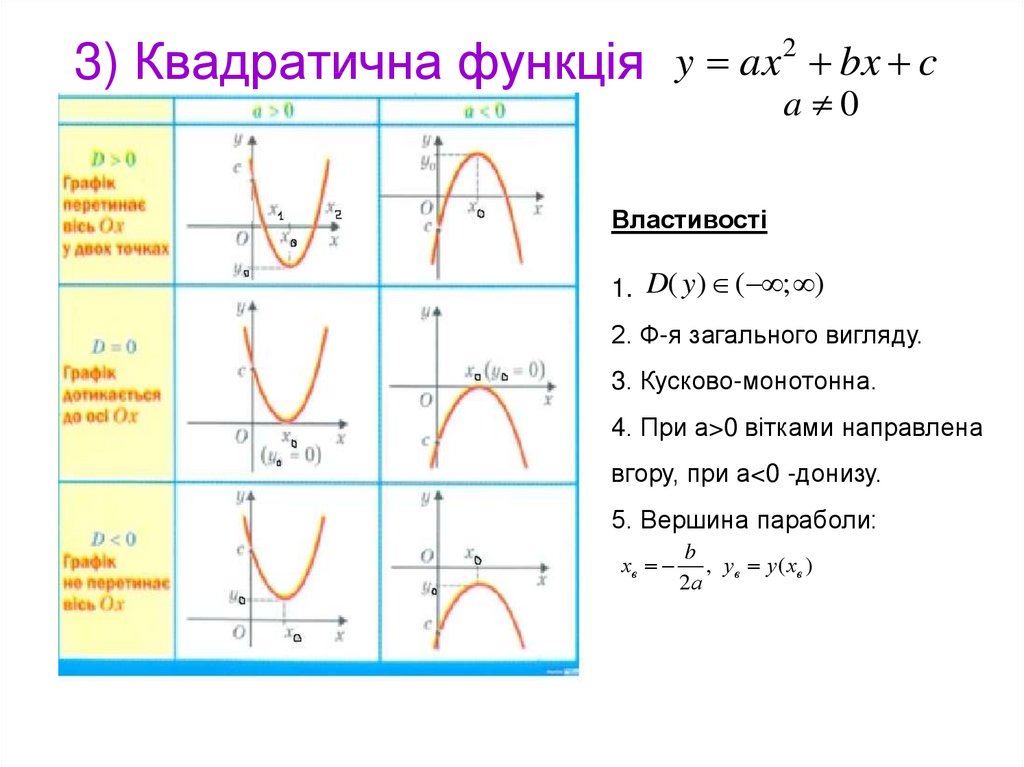
6. 3) Квадратична функція
y ax 2 bx ca 0
Властивості
1. D( y ) ( ; )
2. Ф-я загального вигляду.
3. Кусково-монотонна.
4. При а>0 вітками направлена
вгору, при а<0 -донизу.
5. Вершина параболи:
хв
b
, ув у ( хв )
2а
7. 4) Степенева функція
y x• 1) n - натуральне (n є N)
n - парне
n парне
n 2k ,
k N
n непарне
n 2k 1,
k N
n
8. 2) n – ціле, від’ємне (n є Z)
n парнеn 2k ,
k N
n непарне
n (2k 1),
k N
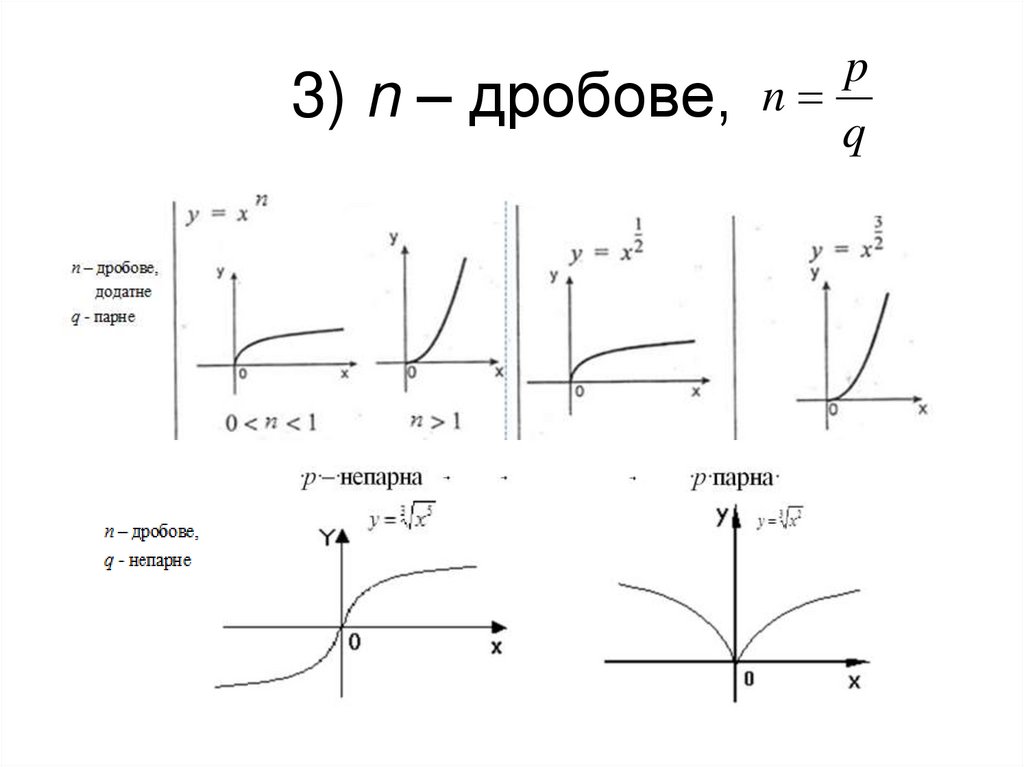
9. 3) n – дробове,
pn
q
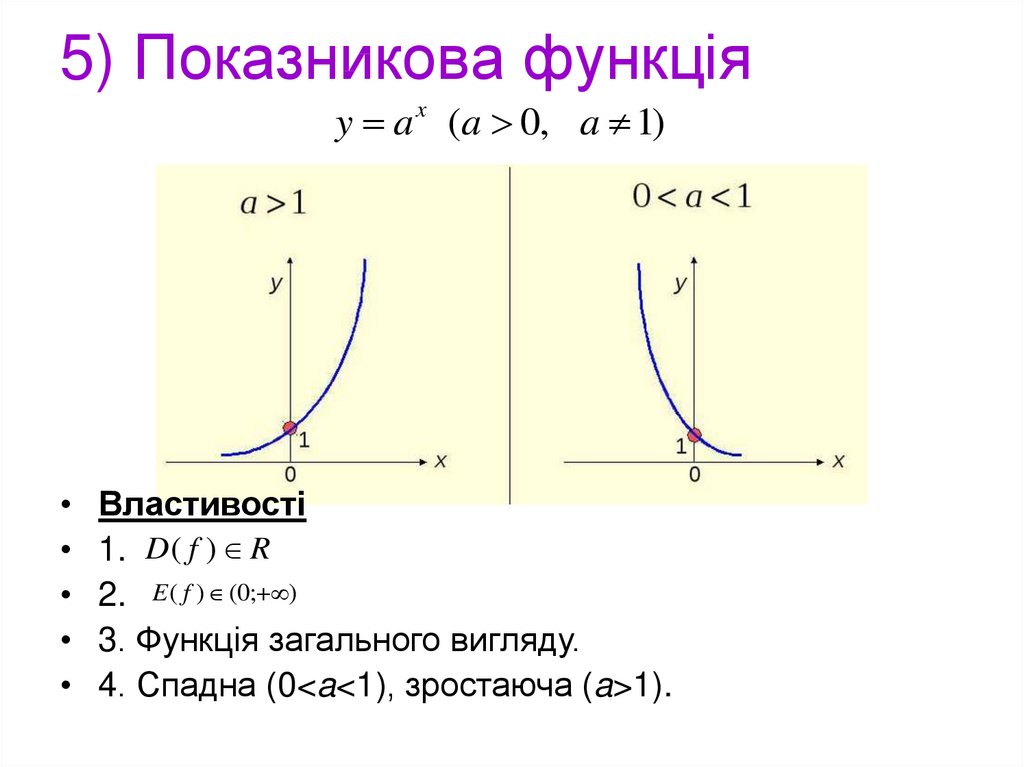
10. 5) Показникова функція
y a x (a 0, a 1)Властивості
1. D ( f ) R
2. E ( f ) (0; )
3. Функція загального вигляду.
4. Спадна (0<a<1), зростаюча (a>1).
11. 6) Логарифмічна функція
y log a x (a 0, a 1)Властивості
1. D( f ) (0; )
2. E ( f ) R
3. Функція загального вигляду.
4. Спадна (0<a<1), зростаюча (a>1).
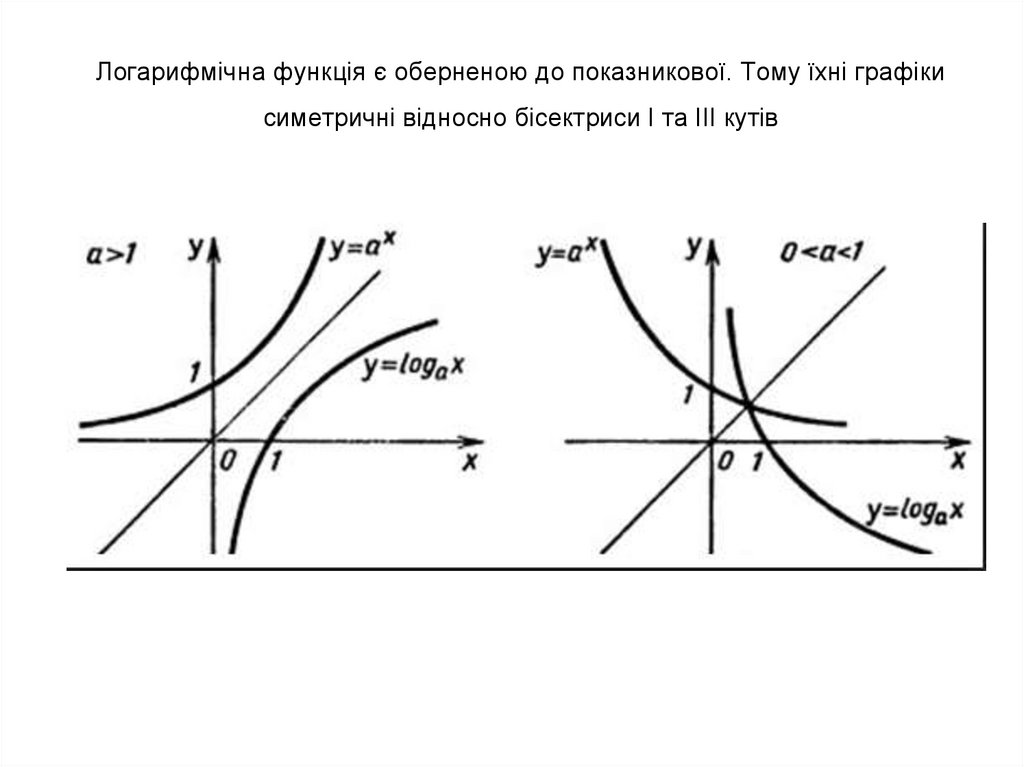
12. Логарифмічна функція є оберненою до показникової. Тому їхні графіки симетричні відносно бісектриси І та ІІІ кутів
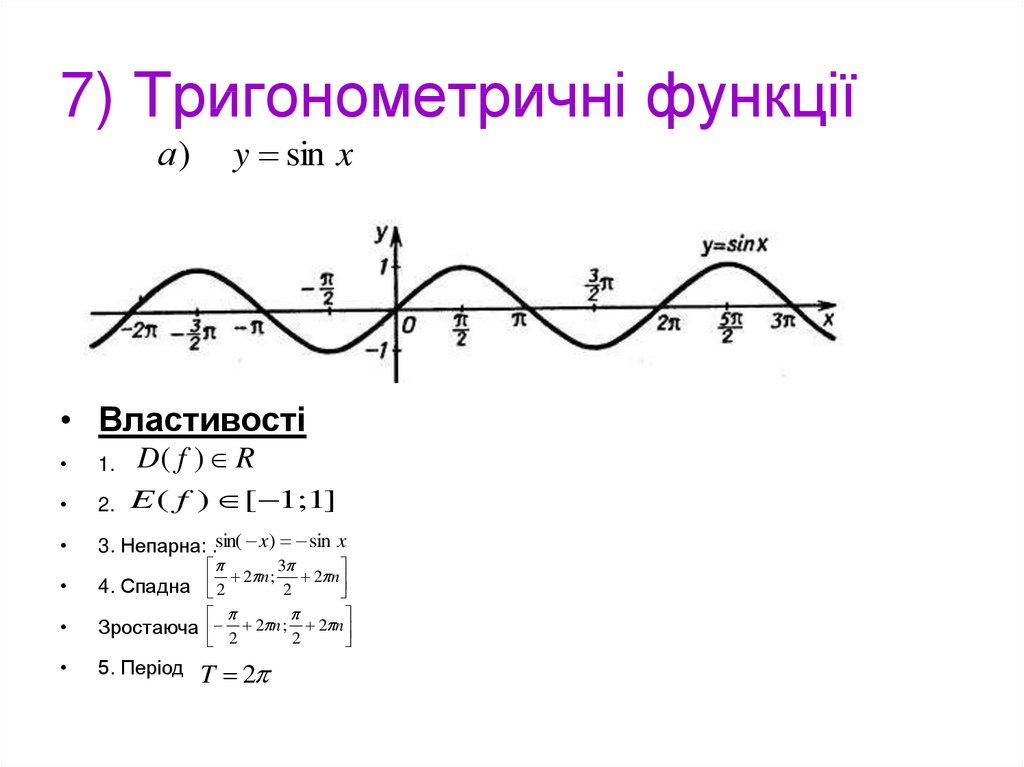
13. 7) Тригонометричні функції
а)y sin x
а)
• Властивості
D( f ) R
1.
2.
3. Непарна: .sin( x) sin x
E ( f ) [ 1;1]
3
2 n ;
2 n
4. Спадна 2
2
Зростаюча 2 2 n ; 2 2 n
5. Період
T 2
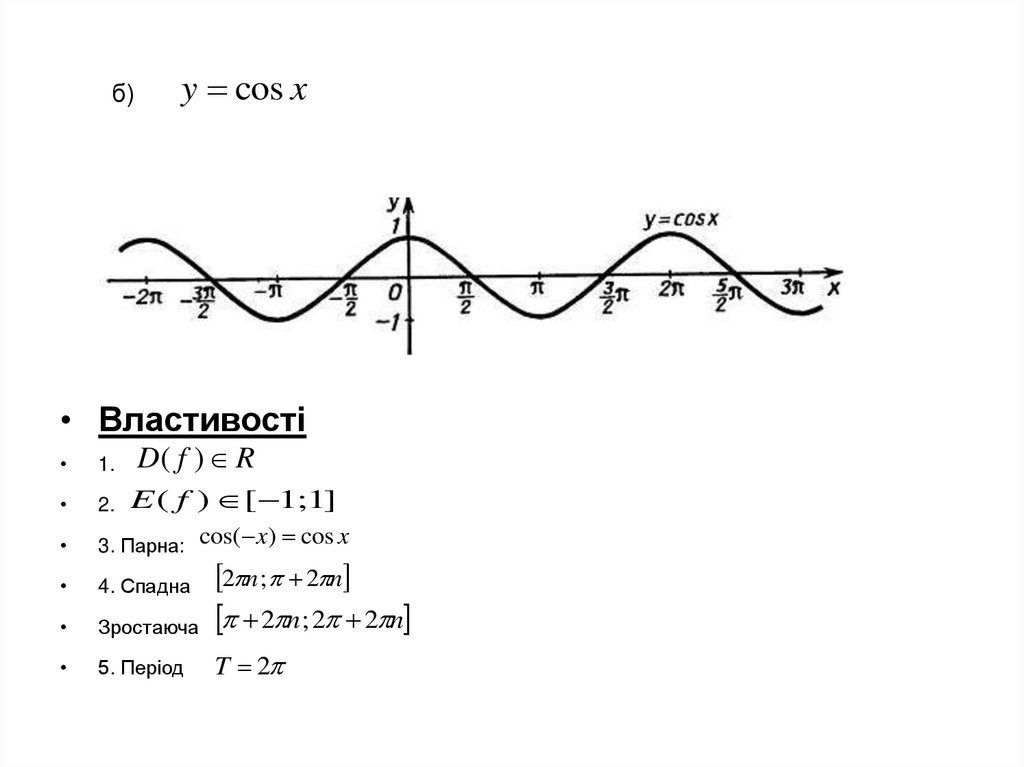
14. б)
y cos x• Властивості
D( f ) R
1.
2.
3. Парна: cos( x) cos x
4. Спадна
Зростаюча
2 n ; 2 2 n
5. Період
T 2
E ( f ) [ 1;1]
2 n ; 2 n
15.
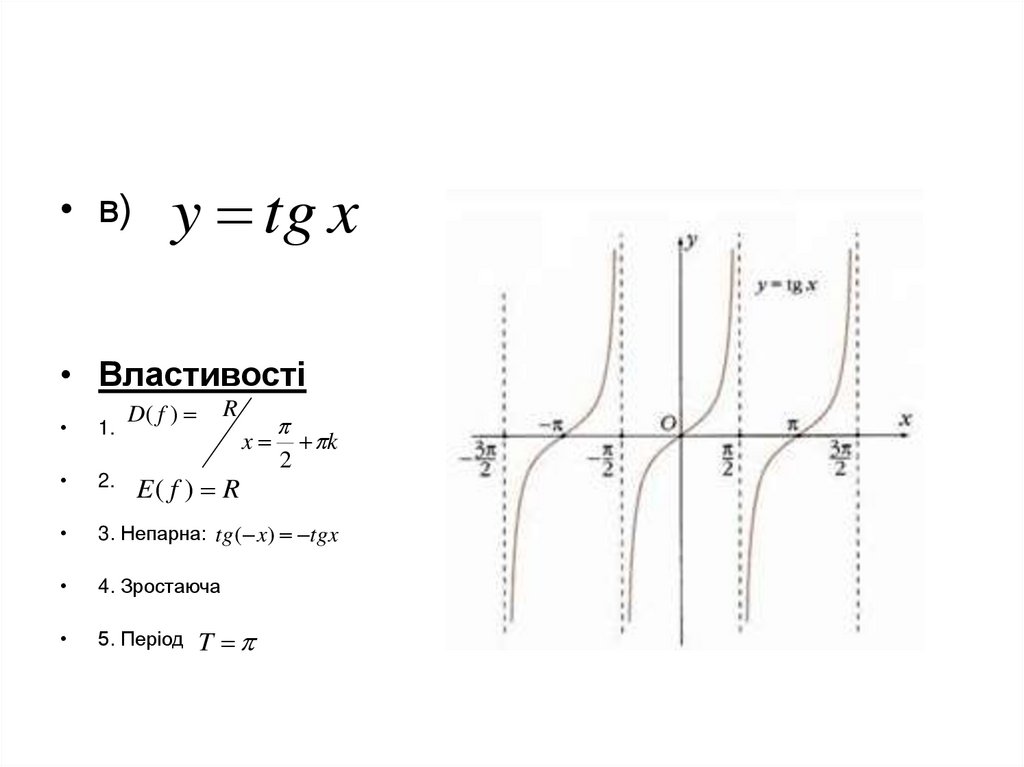
• в)y tg x
• Властивості
D( f )
R
1.
2.
3. Непарна: tg ( x) tgx
4. Зростаюча
5. Період
x
E( f ) R
T
2
k
16.
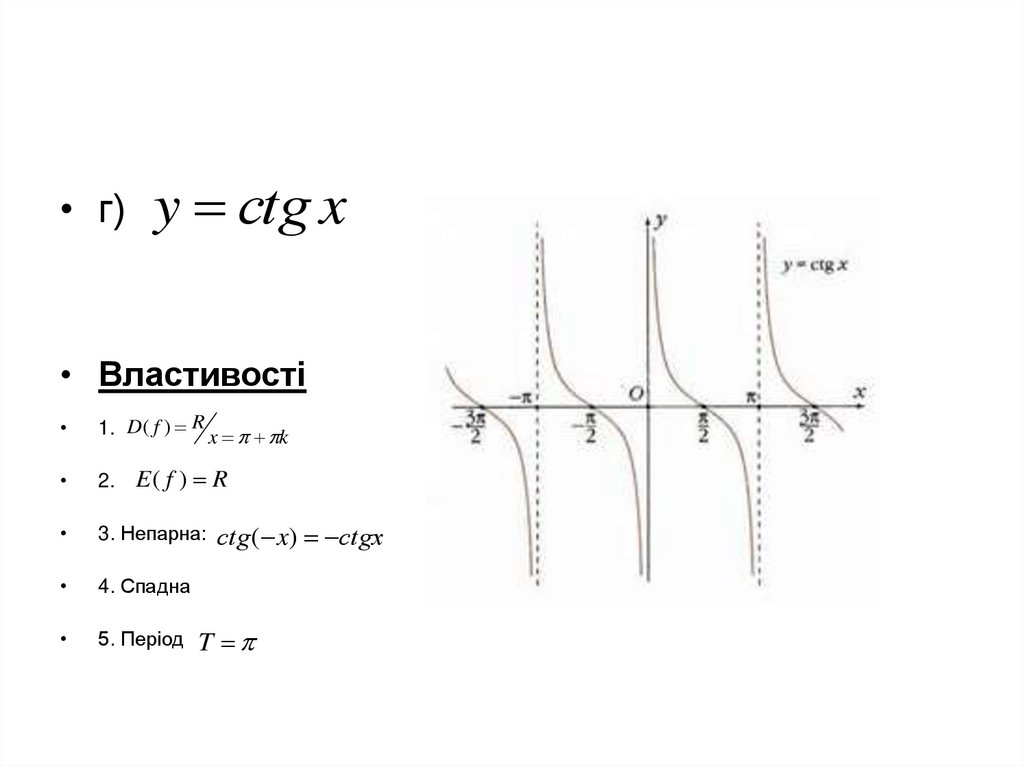
• г)y сtg x
• Властивості
1. D( f ) R x k
2.
3. Непарна:
4. Спадна
5. Період
E( f ) R
сtg ( x) сtgx
T
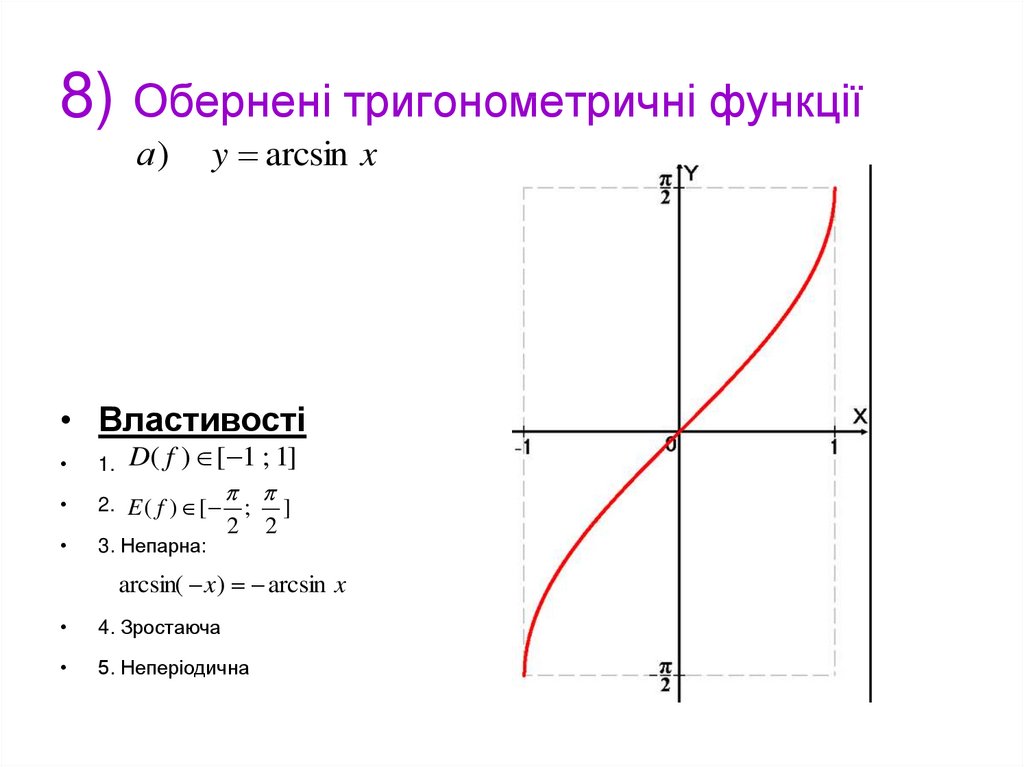
17. 8) Обернені тригонометричні функції
а)y arcsin x
• Властивості
D( f ) [ 1 ; 1]
1.
2. E ( f ) [
3. Непарна:
2
;
2
]
arcsin( x) arcsin x
4. Зростаюча
5. Неперіодична
18.
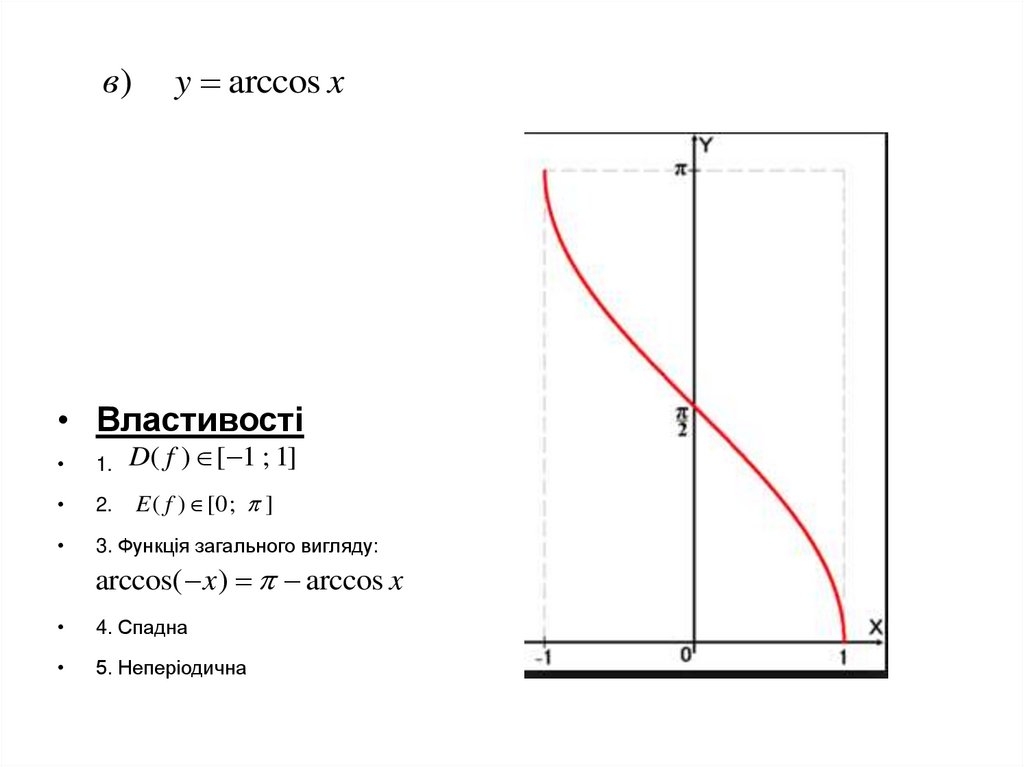
в)y arccos x
• Властивості
D( f ) [ 1 ; 1]
1.
2.
3. Функція загального вигляду:
E ( f ) [0 ; ]
arccos( x) arccos x
4. Спадна
5. Неперіодична
19.
б)y arctg x
• Властивості
D( f ) R
1.
2. E ( f ) (
3. Непарна:
2
;
2
)
arctg ( x) arctgx
4. Зростаюча
5. Неперіодична
20.
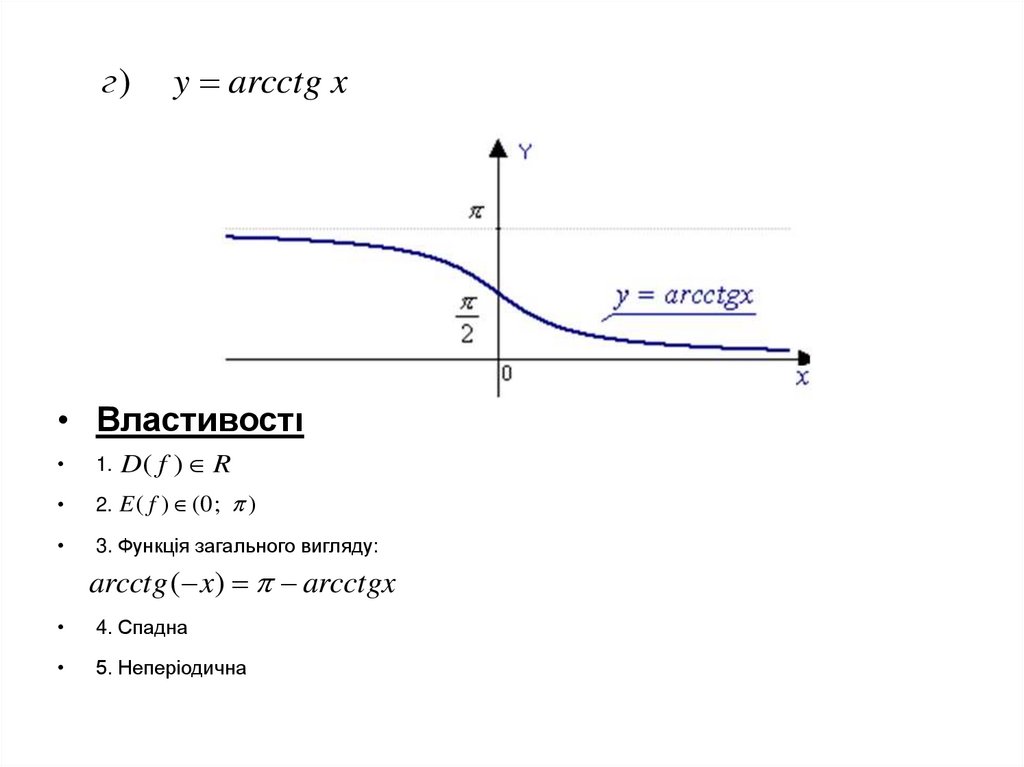
г)y arcctg x
• Властивості
D( f ) R
1.
2. E ( f ) (0 ;
3. Функція загального вигляду:
)
arcctg ( x) arcctgx
4. Спадна
5. Неперіодична
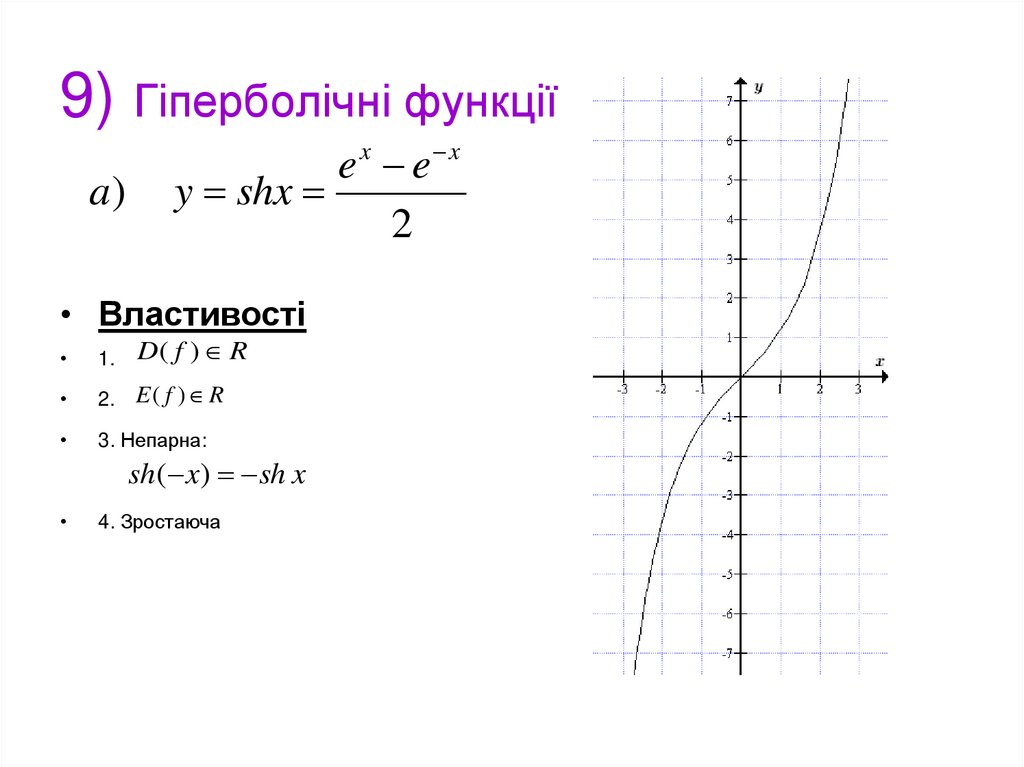
21. 9) Гіперболічні функції
a)e x e x
y shx
2
• Властивості
1.
D( f ) R
2.
E( f ) R
3. Непарна:
sh( x) sh x
4. Зростаюча
22.
e x e xy chx
2
б)
• Властивості
1.
D( f ) R
2.
E ( f ) [1; )
3. Парна:
ch( x) ch x
4. Кусково-монотонна
Зростає при
x [0 ; ]
Спадає при
x [ ; 0]
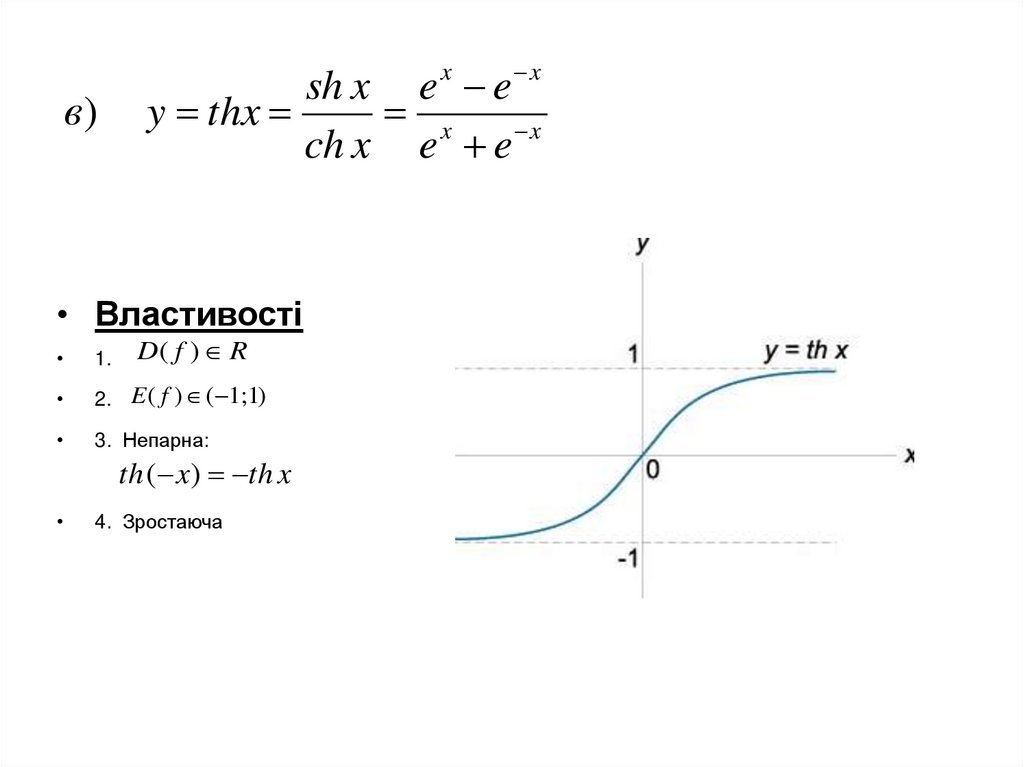
23.
в)sh x e x e x
y thx
x x
ch x e e
• Властивості
D( f ) R
1.
2. E ( f ) ( 1;1)
3. Непарна:
th ( x) th x
4. Зростаюча
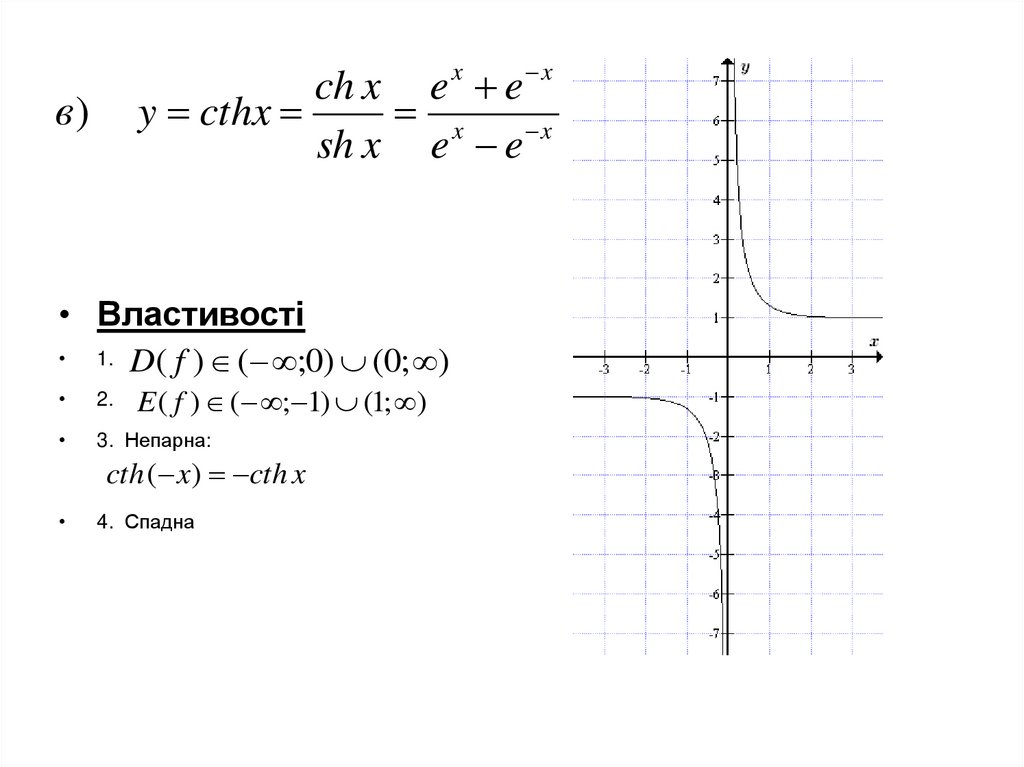
24.
ch x e x e xy cthx
x x
sh x e e
в)
• Властивості
1. D( f ) ( ;0) (0; )
E ( f ) ( ; 1) (1; )
2.
3. Непарна:
cth ( x) cth x
4. Спадна







 mathematics
mathematics








