Similar presentations:
Нелинейная регрессия
1.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Предположим, что переменная Y зависит от переменной X в соответствии с
показанной зависимостью, и необходимо получить оценки b1, b2, и b3, имея данные Y и
X.
1
2.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Представленное выше уравнение не может быть преобразовано в уравнение
линейного вида, поэтому в этом случае невозможно применение обычной процедуры
оценивания регрессии.
2
3.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Тем не менее, все же можно использовать принцип минимизации суммы квадратов
остатков для получения оценок параметров. Мы опишем простой нелинейный
регрессионный алгоритм, который использует принцип, состоящий из серии
повторяющихся шагов.
3
4.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1. Предположение b1, b2, и b3. bˆ , bˆ , и
2
1
приближенные оценки.
bˆ3 -
Начинаем с оценивания правдоподобных значений параметров.
4
5.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1. Предположение b1, b2, и b3.
приближенные оценки.
bˆ1 , bˆ 2 ,
и bˆ 3 -
ˆi bˆ1 bˆ2 X ibˆ3
Y
2. Вычисляем
для каждого исследования.
Вычисляем соответствующие установленные значения Y из данных по X,
обусловленные этими значениями параметров.
5
6.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1.
Предположение b1, b2, и b3.
2.
Вычисляем Yˆ
3.
4.
bˆ1 , bˆ 2 ,
и
bˆ3
- приближенные оценки.
ˆ bˆ X bˆ3 для каждого исследования.
b
i
1
2
i
Вычисляем u
ˆ i Yi Yˆi для каждого исследования.
Вычисляем RSS
uˆ i2 .
Вычисляем остатки для каждого наблюдения в выборке и, следовательно, RSS сумму квадратов остатков.
6
7.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1.
Предположение b1, b2, и b3.
оценки.
2.
Вычисляем
3.
Вычисляем
4.
Вычисляем
5.
Вычисляем
bˆ1 , bˆ 2 ,
и
bˆ3 - приближенные
ˆ
Yˆi bˆ1 bˆ2 X ib 3 для каждого исследования.
uˆ i Yi Yˆi для каждого исследования.
RSS uˆ i2 .
bˆ , bˆ и bˆ
1
2
3
Затем вносим небольшие изменения в одну или более оценку параметров.
7
8.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1.
2.
3.
4.
5.
6.
Nonlinear regression
Предположение
b1, b2, и b3. bˆalgorithm
, bˆ 2 , и bˆ 3 - приближенные
1
оценки.
1. Guess ˆb1, b2ˆ, andˆb3. bbˆ31, b2, and b3 are the guesses.
b 1 b 2 X i для каждого исследования.
2. Calculate Yi = b1 ˆ+ b2Xi for each observation.
ˆ i Yi Yi для каждого исследования.
Вычисляем u
3. Calculate e = Yi – Yi2 for
Вычисляем RSSi
uˆ i . each observation.
4. Calculate
Вычисляем
, bˆ 2= ∑e
и i.bˆ 3
bˆ1RSS
5. Adjust b1, Y
b2, , u
and b3. .
Пересчитываем
i ˆ i , RSS
Вычисляем Yi
6. Re-calculate Yi, ei, RSS.
Используя новые оценки b1, b2, и b3 , пересчитываем установленные значения Y. Затем
пересчитываем остатки и RSS.
8
9.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1.
2.
3.
4.
5.
6.
Предположение b1, b2, и b3.
оценки.
bˆ1 , bˆ 2
, и
bˆ3 - приближенные
ˆ
Yˆi bˆ1 bˆ2 X ib 3 для каждого исследования.
Вычисляем
uˆ i Yi Yˆi для каждого исследования.
Вычисляем RSS u
ˆ i2 .
Вычисляем bˆ , bˆ 2 и bˆ
1
3
Пересчитываем Yi, u
ˆ i , RSS.
Вычисляем
7. Если новый RSS < предыдущего RSS, продолжить вычисление
методом наименьших квадратов.
В противном случае выполнить другое вычисление.
Если RSS меньше стал меньше предыдущего, новые оценки параметров лучше
предыдущих, необходимо продолжать корректировать оценки в одном направлении.
В противном случае необходимо выполнить различные вычисления методом
наименьших квадратов.
9
10.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1. Предположение b1, b2, и b3.
приближенные оценки.
2. Вычисляем
Yˆi
исследования.
bˆ1
,
bˆ 2 ,
и
bˆ3
-
ˆ
bˆ1 bˆ2 X ib 3 для каждого
uˆ i Yi Yˆi для каждого исследования.
4. Вычисляем RSS u
ˆ i2 .
5. Вычисляем bˆ1 , bˆ 2 и bˆ 3
ˆ i , RSS.
6. Пересчитываем Yi, u
3. Вычисляем
7. Если новый RSS < предыдущего RSS, продолжить
вычисление методом наименьших квадратов.
8. Повторите шаги 5, 6 и 7 для сближения.
Вы повторяете шаги 5, 6 и 7 вновь до тех пор, пока не окажется невозможным внести
какие-либо изменения в оценки параметров, которые привели бы к уменьшению RSS.
10
11.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1. Предположение b1, b2, и b3.
приближенные оценки.
2. Вычисляем Yˆ
i
исследования.
bˆ1
ˆ
bˆ1 bˆ2 X ib 3
,
bˆ 2 ,
и
bˆ3
-
для каждого
для каждого исследования.
uˆ i Yi Yˆi
4. Вычисляем
RSS uˆ i2 .
5. Вычисляем bˆ1 , bˆ 2 и bˆ 3
ˆ i , RSS.
6. Пересчитываем Yi, u
3. Вычисляем
7. Если новый RSS < предыдущего RSS, продолжить
вычисление методом наименьших квадратов.
8. Повторите шаги 5, 6 и 7 для сближения.
Делается вывод о том, что величина RSS минимизирована и конечные оценки
параметров являются оценками по методу наименьших квадратов.
11
12.
НЕЛИНЕЙНАЯ РЕГРЕССИЯY b1 b 2 X b3 u
Алгоритм нелинейной регрессии
1. Предположение b1, b2, и b3.
приближенные оценки.
2. Вычисляем Yˆ
i
исследования.
bˆ1
ˆ
bˆ1 bˆ2 X ib 3
,
bˆ 2 ,
и
bˆ3
-
для каждого
для каждого исследования.
uˆ i Yi Yˆi
4. Вычисляем RSS u
ˆ i2 .
5. Вычисляем bˆ1 , bˆ 2 и bˆ 3
ˆ i , RSS.
6. Пересчитываем Yi, u
3. Вычисляем
7. Если новый RSS < предыдущего RSS, продолжить
вычисление методом наименьших квадратов.
8. Повторите шаги 5, 6 и 7 для сближения.
Следует подчеркнуть, что математики давно разработали сложные методы, чтобы
свести к минимуму количество шагов, требуемых алгоритмами этого типа.
12
13.
НЕЛИНЕЙНАЯ РЕГРЕССИЯe b1
b2
g
u
Employment growth rate
3
2
1
0
0
1
2
3
4
5
6
7
8
9
GDP growth rate
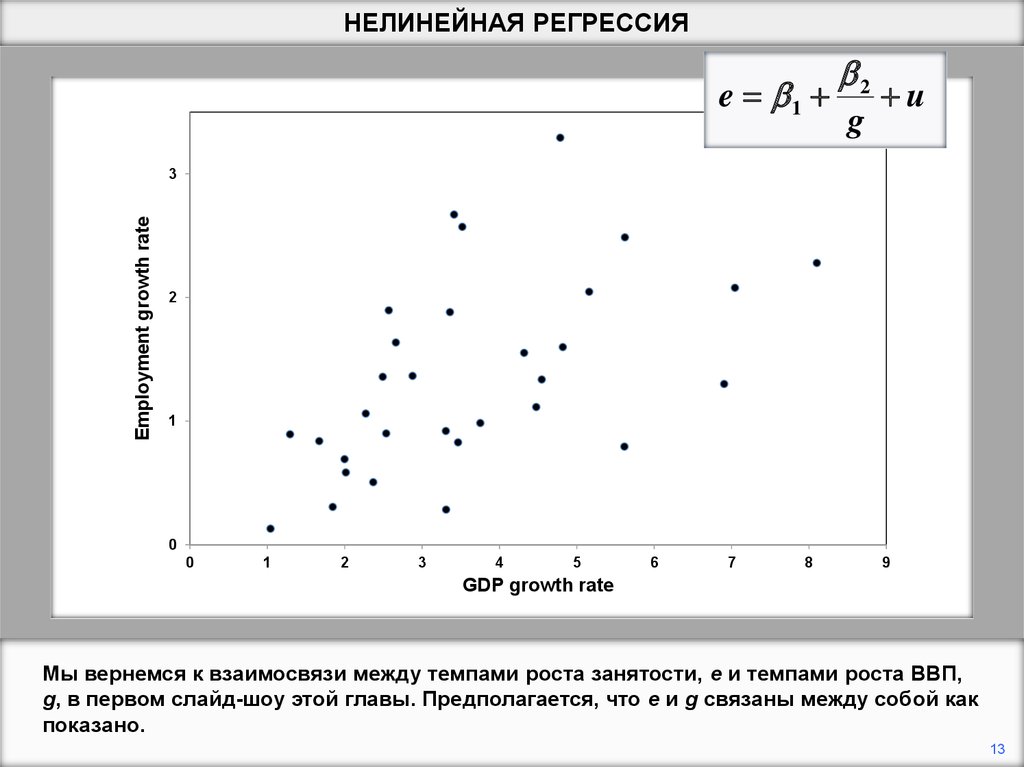
Мы вернемся к взаимосвязи между темпами роста занятости, е и темпами роста ВВП,
g, в первом слайд-шоу этой главы. Предполагается, что e и g связаны между собой как
показано.
13
14.
НЕЛИНЕЙНАЯ РЕГРЕССИЯe b1
b2
g
u
Employment growth rate
3
2
1
0
0
1
2
3
4
5
6
7
8
9
GDP growth rate
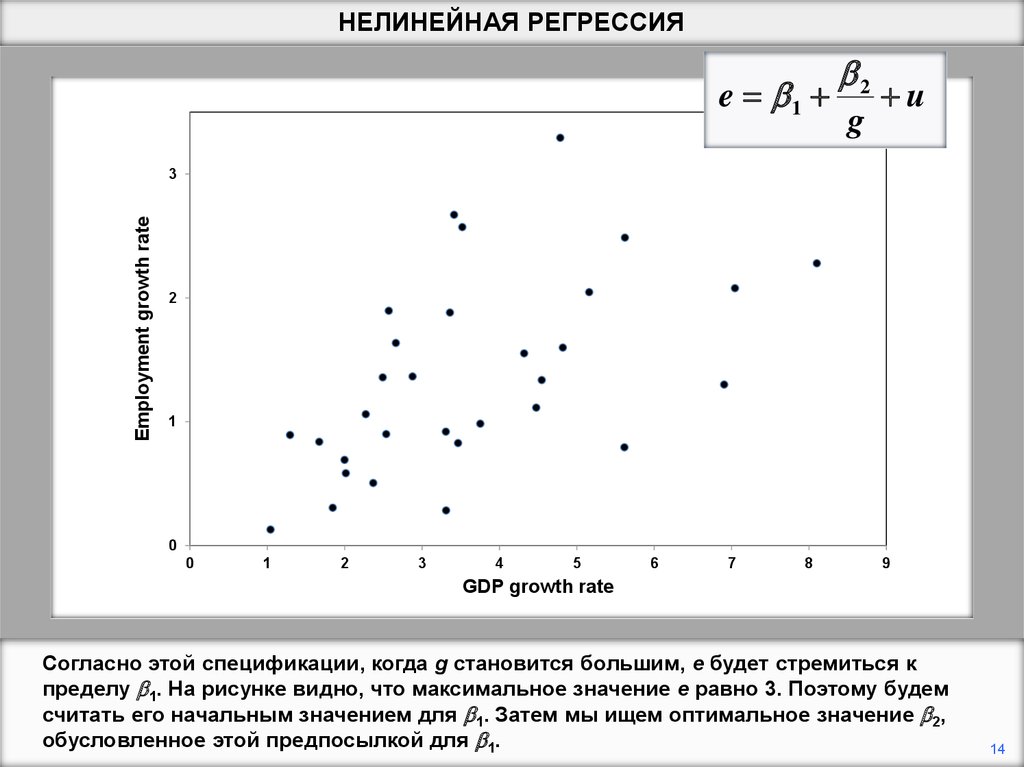
Согласно этой спецификации, когда g становится большим, e будет стремиться к
пределу b1. На рисунке видно, что максимальное значение e равно 3. Поэтому будем
считать его начальным значением для b1. Затем мы ищем оптимальное значение b2,
обусловленное этой предпосылкой для b1.
14
15.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ400
RSS
Условное значение bˆ1 3
300
200
-7
-6
-5
–4.22 -4
-3
-2
-1
0
estimate of b2
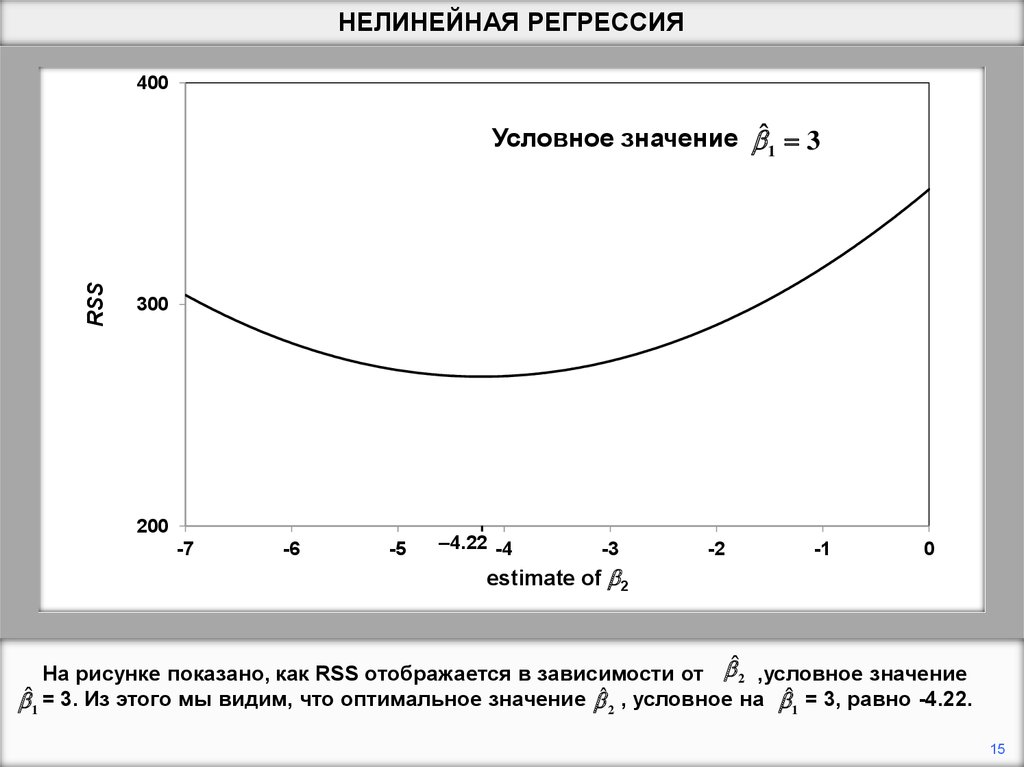
На рисунке показано, как RSS отображается в зависимости от bˆ2 ,условное значение
bˆ1 = 3. Из этого мы видим, что оптимальное значение bˆ 2 , условное на bˆ1 = 3, равно -4.22.
15
16.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ200
RSS
Условное значение bˆ2 4.22
100
0
1
2
2.82 3
estimate of b1
4
b1
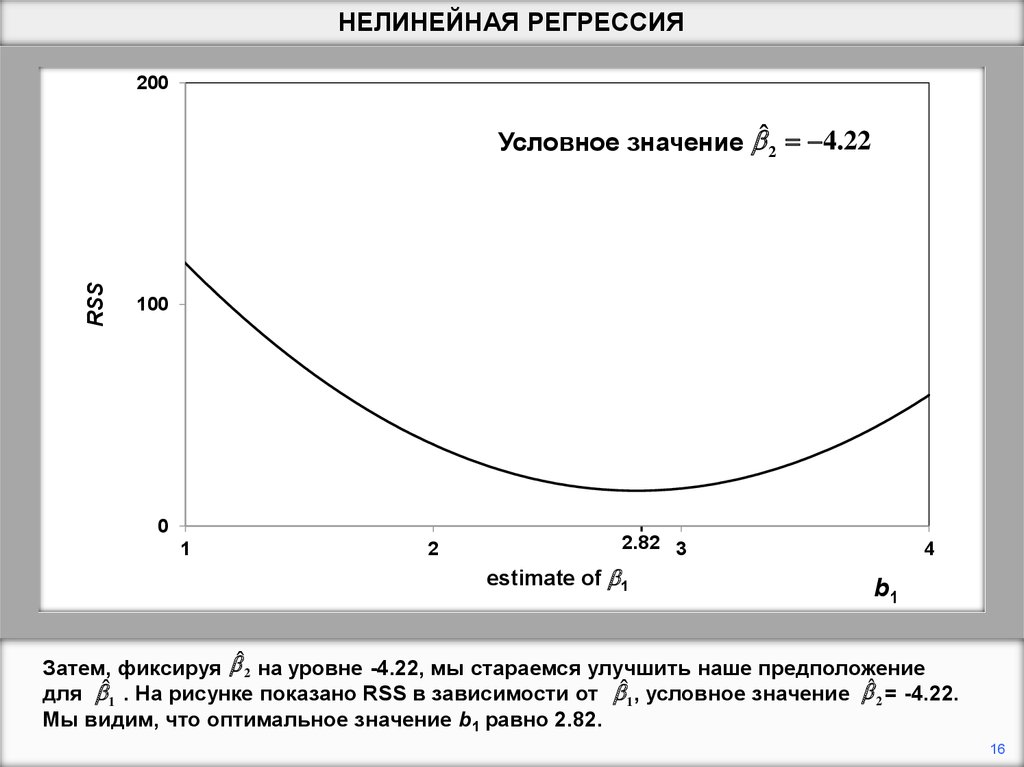
Затем, фиксируя bˆ 2 на уровне -4.22, мы стараемся улучшить наше предположение
для bˆ1 . На рисунке показано RSS в зависимости от bˆ1 , условное значение bˆ 2 = -4.22.
Мы видим, что оптимальное значение b1 равно 2.82.
16
17.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ200
RSS
Условное значение bˆ2 4.22
100
0
1
2
2.82 3
estimate of b1
4
b1
Мы продолжаем делать так до тех пор, пока обе оценки параметров сходятся к
пределам и затем перестают меняться. Затем мы достигнем значений, которые дают
минимальную сумму квадратов остатков (RSS).
17
18.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ200
RSS
Условное значение bˆ2 4.22
100
0
1
2
2.82 3
estimate of b1
4
b1
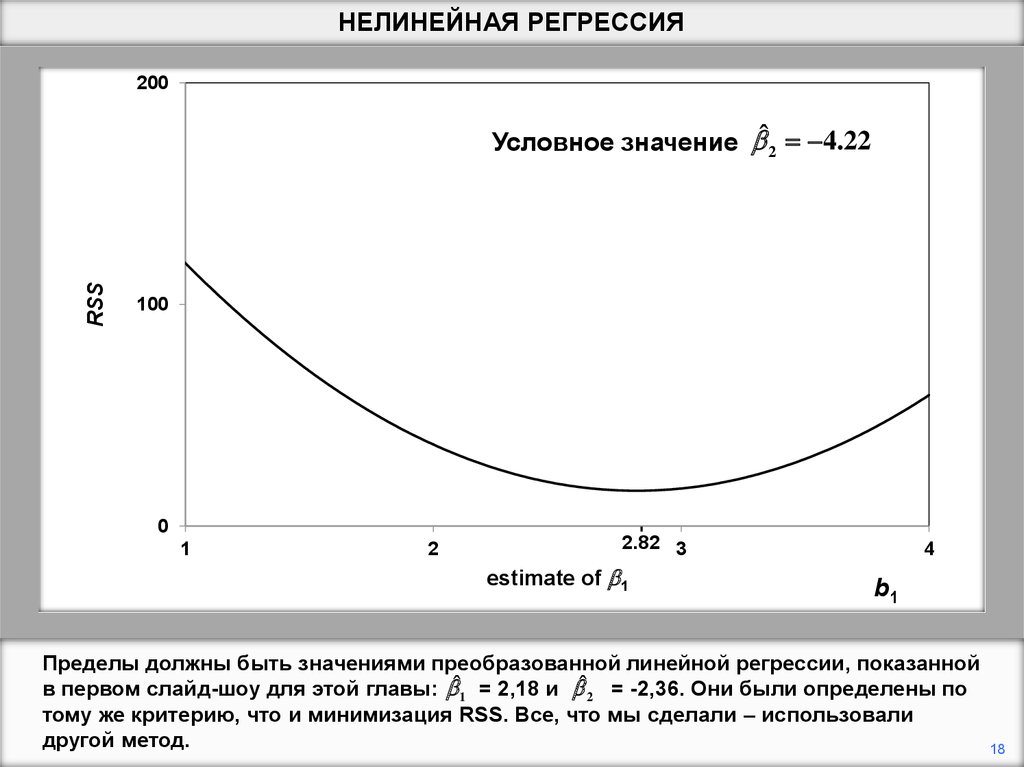
Пределы должны быть значениями преобразованной линейной регрессии, показанной
в первом слайд-шоу для этой главы: bˆ1 = 2,18 и bˆ 2 = -2,36. Они были определены по
тому же критерию, что и минимизация RSS. Все, что мы сделали – использовали
другой метод.
18
19.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. nl (e = {beta1} + {beta2}/g)
(obs = 31)
Iteration 0:
Iteration 1:
residual SS =
residual SS =
12.30411
12.30411
e b1
b2
g
u
---------------------------------------------------------------------------Source |
SS
df
MS
-----------+-----------------------------Number of obs =
31
Model | 5.80515805
1 5.80515805
R-squared
=
0.3206
Residual |
12.304107
29
.42427955
Adj R-squared =
0.2971
-----------+-----------------------------Root MSE
= .6513674
Total |
18.109265
30 .603642167
Res. dev.
= 59.32851
---------------------------------------------------------------------------e |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------/beta1 |
2.17537
.249479
8.72
0.000
1.665128
2.685612
/beta2 | -2.356136
.6369707
-3.70
0.001
-3.658888
-1.053385
----------------------------------------------------------------------------
Вот результат для данной гиперболической регрессии влияния e на g с
использованием нелинейной регрессии. Это, как обычно, вывод Stata, но вывод из
других приложений регрессии будет похожим.
19
20.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. nl (e = {beta1} + {beta2}/g)
(obs = 31)
Iteration 0:
Iteration 1:
residual SS =
residual SS =
12.30411
12.30411
e b1
b2
g
u
---------------------------------------------------------------------------Source |
SS
df
MS
-----------+-----------------------------Number of obs =
31
Model | 5.80515805
1 5.80515805
R-squared
=
0.3206
Residual |
12.304107
29
.42427955
Adj R-squared =
0.2971
-----------+-----------------------------Root MSE
= .6513674
Total |
18.109265
30 .603642167
Res. dev.
= 59.32851
---------------------------------------------------------------------------e |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------/beta1 |
2.17537
.249479
8.72
0.000
1.665128
2.685612
/beta2 | -2.356136
.6369707
-3.70
0.001
-3.658888
-1.053385
----------------------------------------------------------------------------
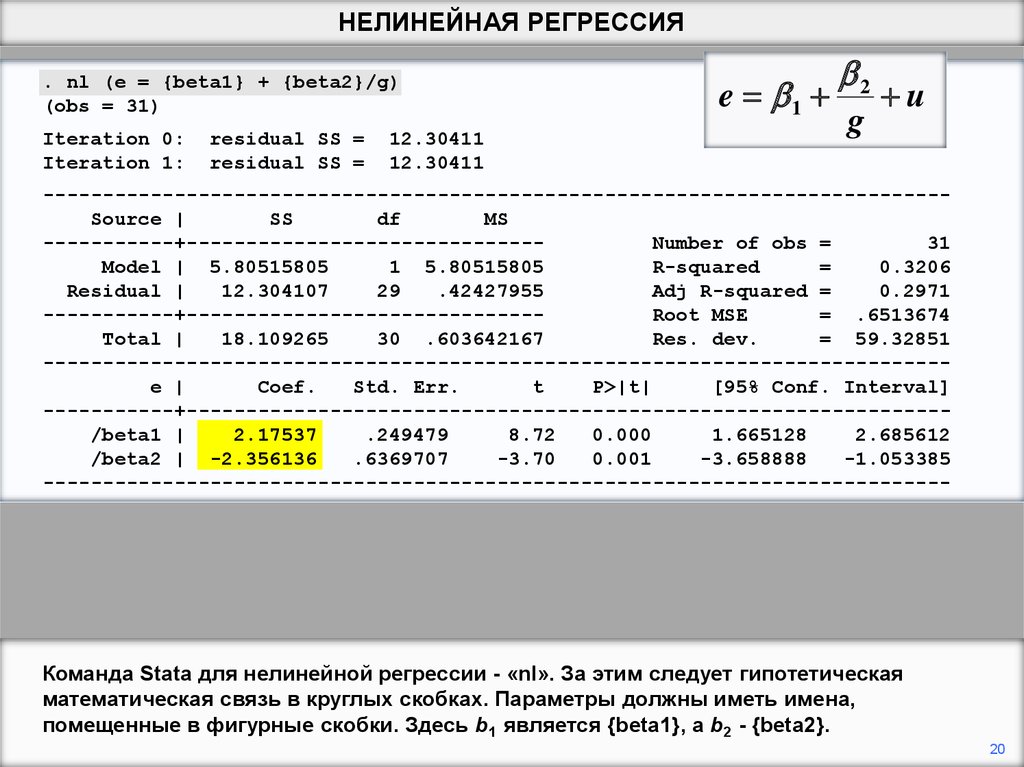
Команда Stata для нелинейной регрессии - «nl». За этим следует гипотетическая
математическая связь в круглых скобках. Параметры должны иметь имена,
помещенные в фигурные скобки. Здесь b1 является {beta1}, а b2 - {beta2}.
20
21.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. gen z = 1/g
. reg e z
e b1
b2
g
u
---------------------------------------------------------------------------Source |
SS
df
MS
Number of obs =
31
-----------+-----------------------------F( 1,
29) =
13.68
Model | 5.80515811
1 5.80515811
Prob > F
= 0.0009
Residual | 12.3041069
29 .424279548
R-squared
= 0.3206
-----------+-----------------------------Adj R-squared = 0.2971
Total |
18.109265
30 .603642167
Root MSE
= .65137
---------------------------------------------------------------------------e |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------z | -2.356137
.6369707
-3.70
0.001
-3.658888
-1.053385
_cons |
2.17537
.249479
8.72
0.000
1.665128
2.685612
----------------------------------------------------------------------------
2.36
eˆ 2.18 2.36 z 2.18
g
Выходные данные аналогичны выходным данным линейной регрессии в первом
слайд-шоу для этой главы.
21
22.
НЕЛИНЕЙНАЯ РЕГРЕССИЯe b1
4
b2
g
u
Employment growth rate
3
2
1
0
0
1
2
3
4
5
6
7
8
9
-1
-2
-3
GDP growth rate
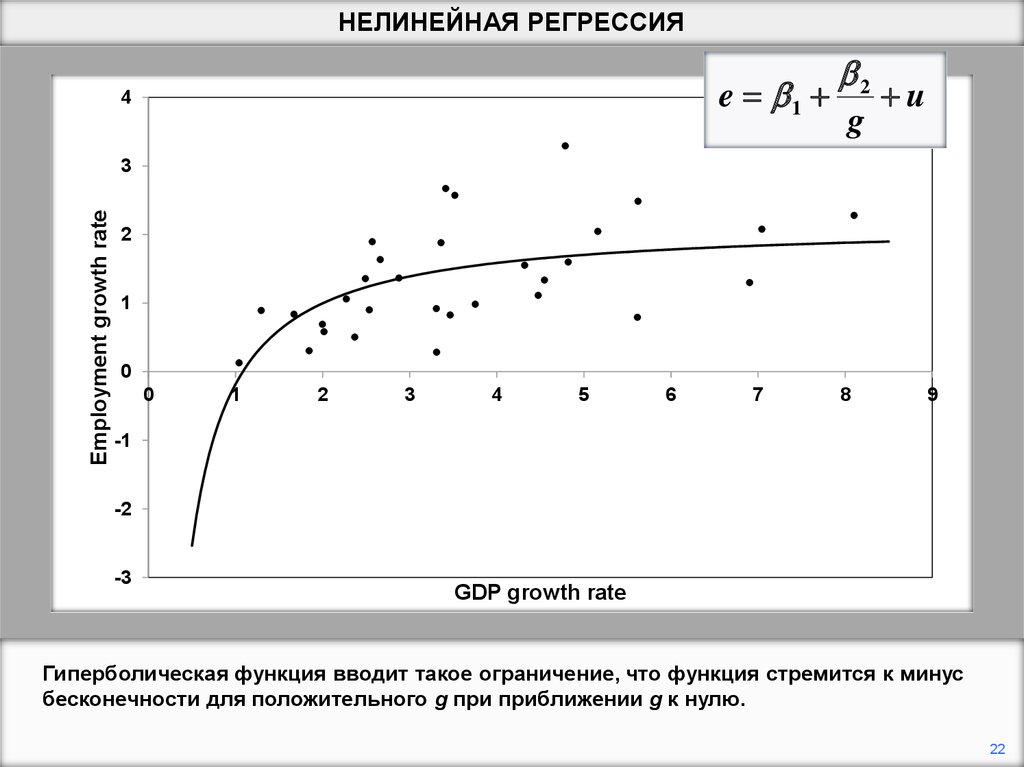
Гиперболическая функция вводит такое ограничение, что функция стремится к минус
бесконечности для положительного g при приближении g к нулю.
22
23.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. nl (e = {beta1} + {beta2}/({beta3} + g))
(obs = 31)
Iteration 0: residual SS = 12.30411
Iteration 1: residual SS = 12.27327
.....................................
Iteration 8: residual SS = 11.98063
e b1
b2
b3 g
u
---------------------------------------------------------------------------Source |
SS
df
MS
-----------+-----------------------------Number of obs =
31
Model | 6.12863996
2 3.06431998
R-squared
=
0.3384
Residual | 11.9806251
28 .427879466
Adj R-squared =
0.2912
-----------+-----------------------------Root MSE
=
.654125
Total |
18.109265
30 .603642167
Res. dev.
=
58.5026
---------------------------------------------------------------------------e |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------/beta1 |
2.714411
1.017058
2.67
0.013
.6310616
4.79776
/beta2 | -6.140415
8.770209
-0.70
0.490
-24.10537
11.82454
/beta3 |
1.404714
2.889556
0.49
0.631
-4.514274
7.323702
----------------------------------------------------------------------------
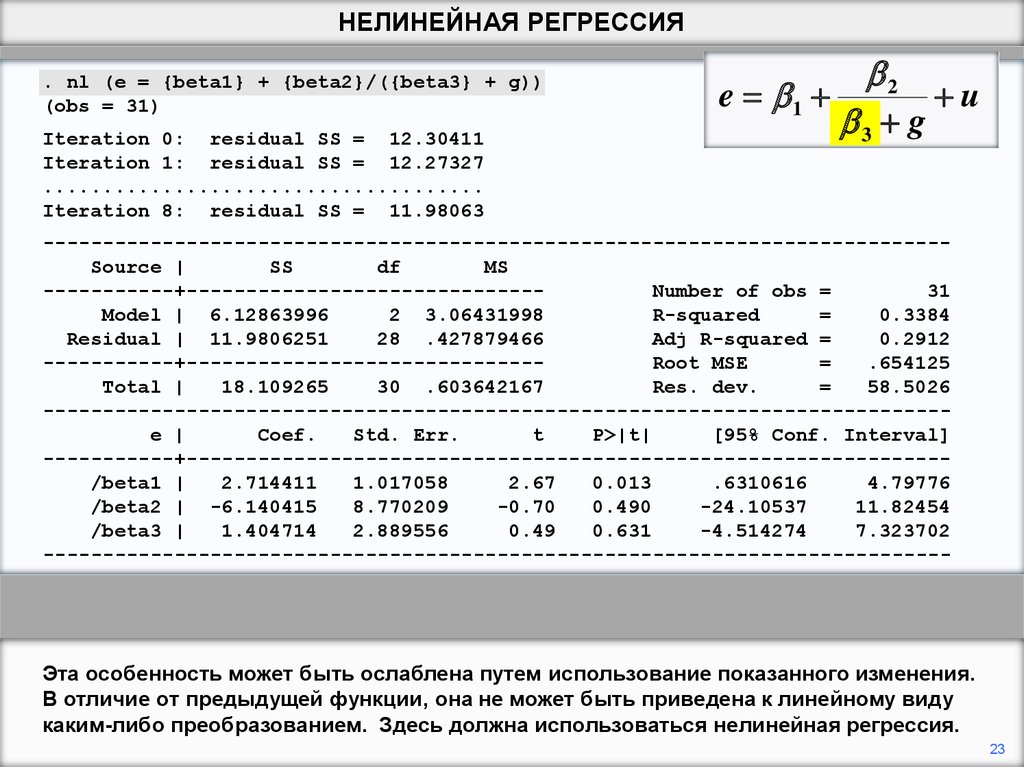
Эта особенность может быть ослаблена путем использование показанного изменения.
В отличие от предыдущей функции, она не может быть приведена к линейному виду
каким-либо преобразованием. Здесь должна использоваться нелинейная регрессия.
23
24.
НЕЛИНЕЙНАЯ РЕГРЕССИЯ. nl (e = {beta1} + {beta2}/({beta3} + g))
(obs = 31)
Iteration 0: residual SS = 12.30411
Iteration 1: residual SS = 12.27327
.....................................
Iteration 8: residual SS = 11.98063
e b1
b2
b3 g
u
---------------------------------------------------------------------------Source |
SS
df
MS
-----------+-----------------------------Number of obs =
31
Model | 6.12863996
2 3.06431998
R-squared
=
0.3384
Residual | 11.9806251
28 .427879466
Adj R-squared =
0.2912
-----------+-----------------------------Root MSE
=
.654125
Total |
18.109265
30 .603642167
Res. dev.
=
58.5026
---------------------------------------------------------------------------e |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-----------+---------------------------------------------------------------/beta1 |
2.714411
1.017058
2.67
0.013
.6310616
4.79776
/beta2 | -6.140415
8.770209
-0.70
0.490
-24.10537
11.82454
/beta3 |
1.404714
2.889556
0.49
0.631
-4.514274
7.323702
----------------------------------------------------------------------------
Вывод для данной спецификации (характеристик) показан с наибольшим количеством
сообщений.
24
25.
НЕЛИНЕЙНАЯ РЕГРЕССИЯe b1
4
b2
b3 g
u
3
Employment growth rate
(4.47)
2
(4.46)
1
0
0
1
2
3
4
5
6
7
8
9
-1
-2
-3
GDP growth rate
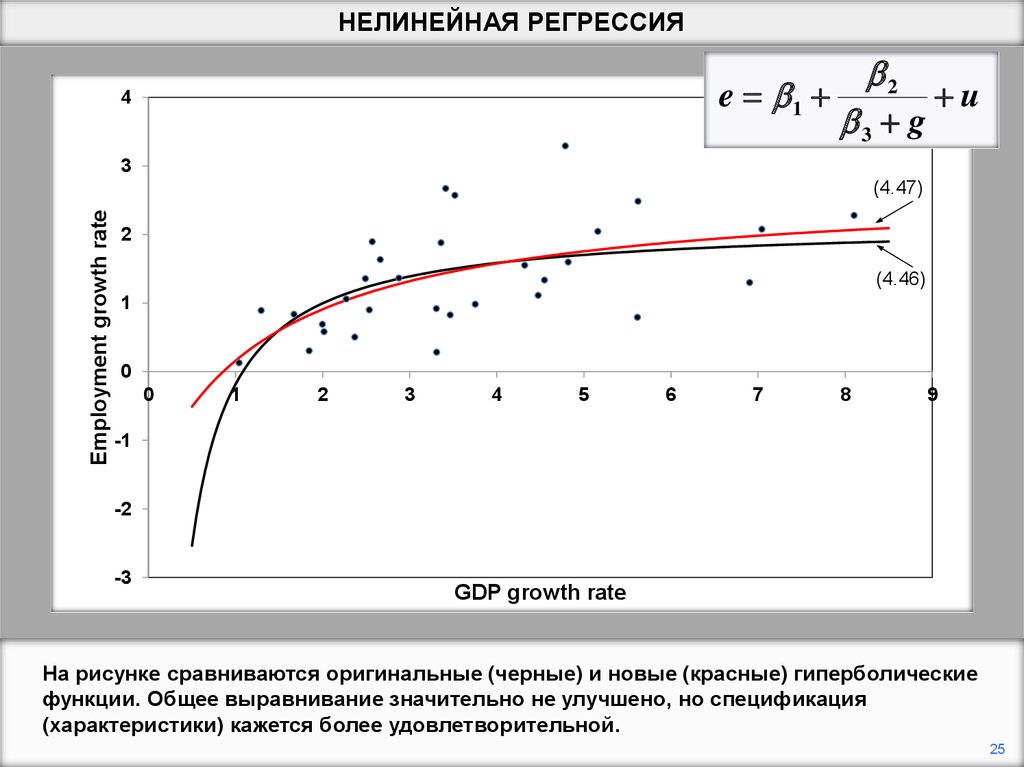
На рисунке сравниваются оригинальные (черные) и новые (красные) гиперболические
функции. Общее выравнивание значительно не улучшено, но спецификация
(характеристики) кажется более удовлетворительной.
25
















 mathematics
mathematics








