688.27K

Category: $mathematics$ mathematics

Вычисление линейных коэффициентов регрессии

1.

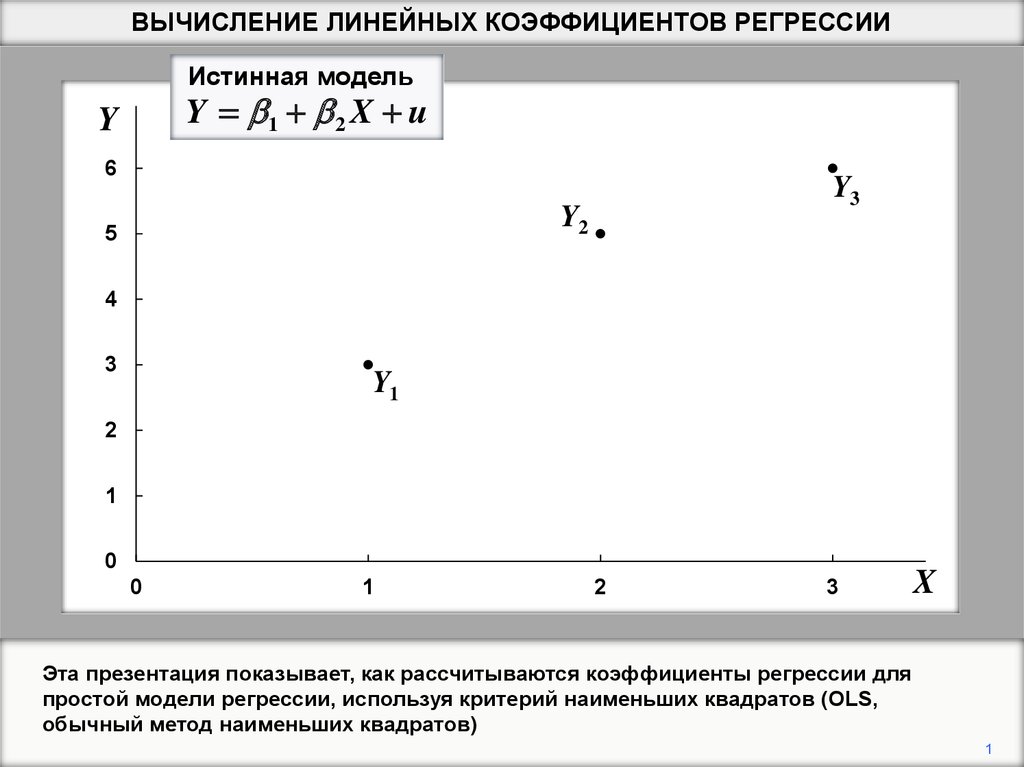
ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y 1 2 X u
Y
6
Y3
Y2
5
4
3
Y1
2
1
0
0
1
2
3
X
Эта презентация показывает, как рассчитываются коэффициенты регрессии для
простой модели регрессии, используя критерий наименьших квадратов (OLS,
обычный метод наименьших квадратов)
1

2.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y 1 2 X u
Y
6
Y3
Y2
5
4
3
Y1
2
1
0
0
1
2
3
X
Начнем с численного примера, имеющего всего три наблюдениями: (1,3), (2,5) и (3,6).
2

3.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y
Y 1 2 X u
6
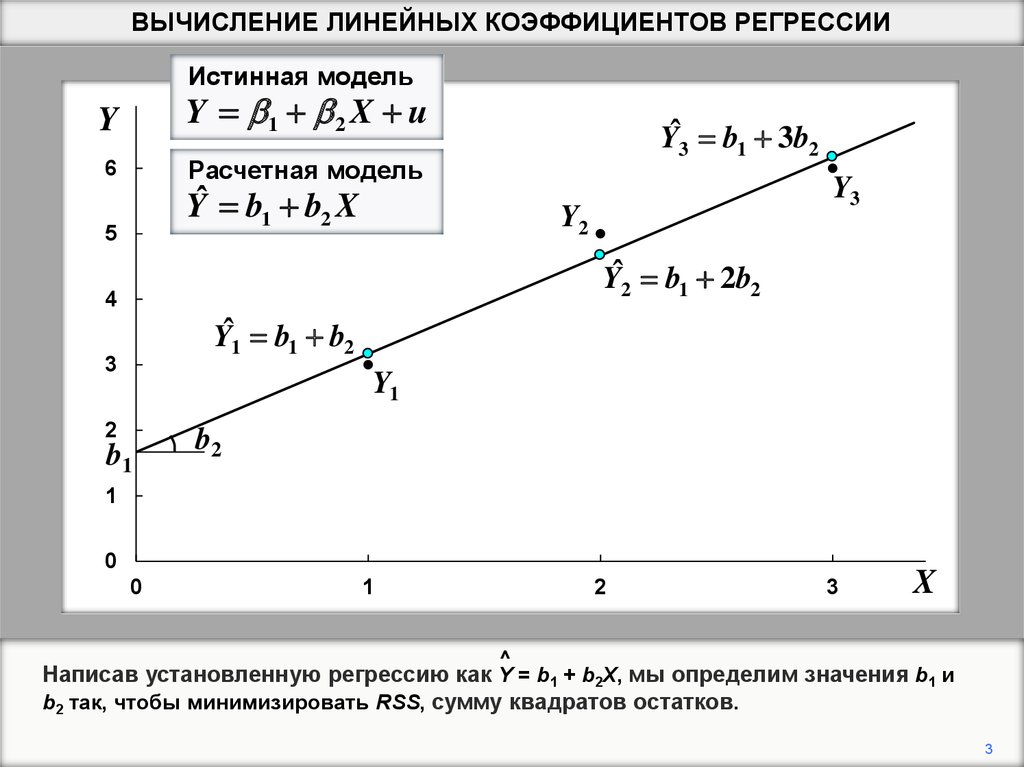
Расчетная модель
Yˆ3 b1 3b2
Yˆ b1 b2 X
5
Y3
Y2
Yˆ2 b1 2b2
4
Yˆ1 b1 b2
3
Y1
2
b1
b2
1
0
0
1
2
3
X
^
Написав установленную регрессию как Y = b1 + b2X, мы определим значения b1 и
b2 так, чтобы минимизировать RSS, сумму квадратов остатков.
3

4.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y
Y 1 2 X u
6
Расчетная модель
Yˆ b1 b2 X
5
Yˆ3 b1 3b2
Y3
Y2
Yˆ2 b1 2b2
4
Yˆ1 b1 b2
3
e1 Y1 Yˆ1 3 b1 b2
e2 Y2 Yˆ2 5 b1 2b2
Y1
2
b1
b2
e3 Y3 Yˆ3 6 b1 3b2
1
0
0
1
2
3
X
Учитывая наш выбор b1 и b2, остатки показаны на рисунке.
4

5.

6.

7.

8.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
RSS
0 12b1 28b2 62 0
b2
Как минимум, частные производные RSS по отношению к b1 и b2 должны быть равны
нулю. (Мы также должны проверить условие второго порядка.)
8

9.

10.

11.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y
Y 1 2 X u
6
Расчетная модель
Yˆ b1 b2 X
5
Yˆ3 b1 3b2
Y3
Y2
Yˆ2 b1 2b2
4
Yˆ1 b1 b2
3
Y1
2
b1
b2
1
0
0
1
2
3
X
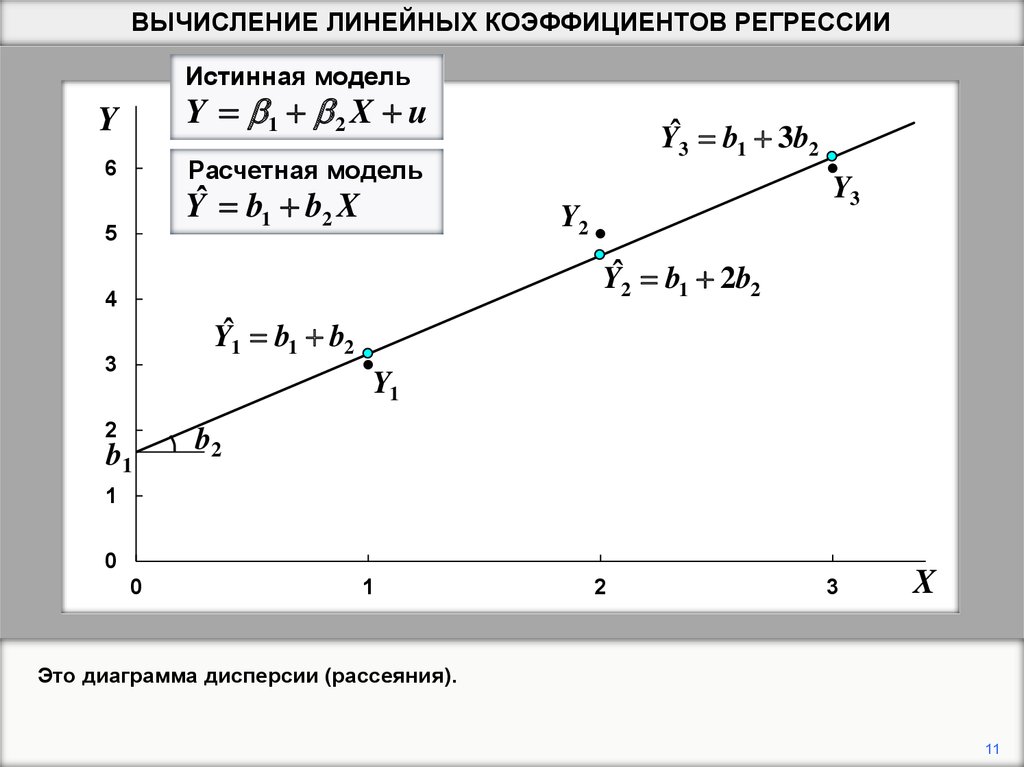
Это диаграмма дисперсии (рассеяния).
11

12.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y
Y 1 2 X u
6
Расчетная модель
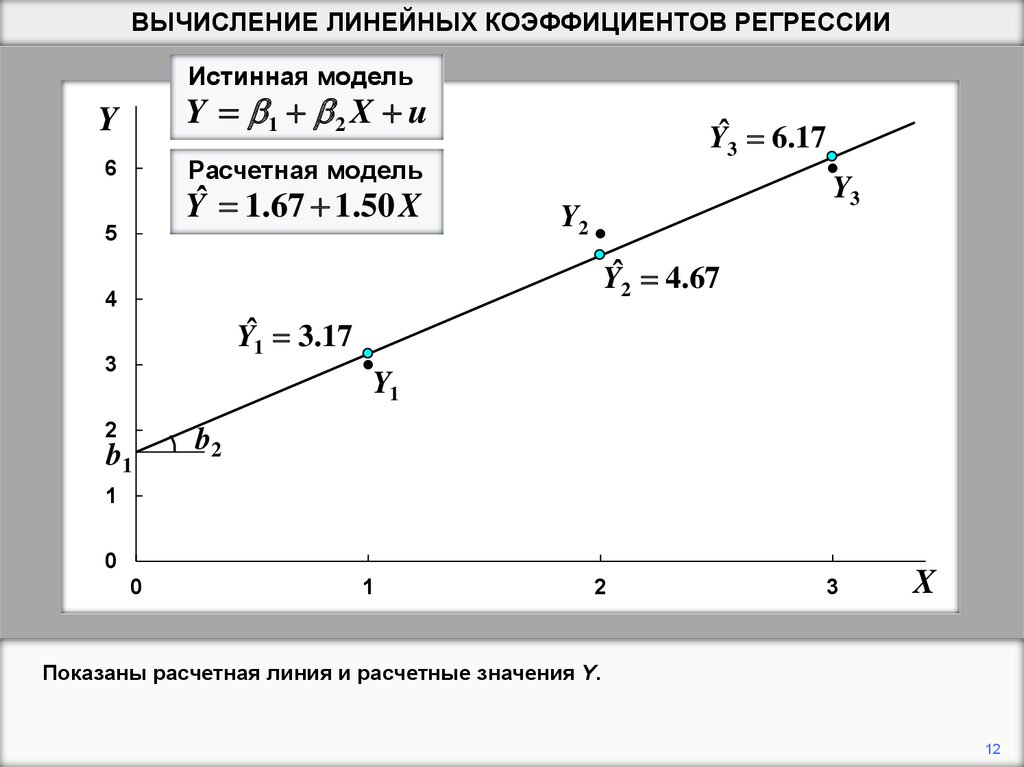
Yˆ 1.67 1.50 X
5
Yˆ3 6.17
Y3
Y2
Yˆ2 4.67
4
Yˆ1 3.17
3
Y1
2
b1
b2
1
0
0
1
2
3
X
Показаны расчетная линия и расчетные значения Y.
12

13.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
RSS
0 12b1 28b2 62 0
b2
b1 1.67, b2 1.50
Прежде чем перейти к общему случаю, нужно сделать небольшое, но важное
математическое замечание.
13

14.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
RSS
0 12b1 28b2 62 0
b2
b1 1.67, b2 1.50
Когда мы устанавливаем выражение для RSS, мы делаем это как функцию от b1 и b2.
На этом этапе b1 и b2 не являются конкретными значениями. Наша задача - определить
конкретные значения, которые минимизируют RSS.
14

15.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
RSS
0 12b1 28b2 62 0
b2
b1 1.67, b2 1.50
Мы должны дать этим значениям собственные названия, чтобы отличать их от всех
остальных.
15

16.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1OLS 12b2OLS 28 0
b1
RSS
0 12b1OLS 28b2OLS 62 0
b2
b1OLS 1.67, b2OLS 1.50
Обозначим значения, которые минимизируют RSS, следующим образом: b1OLS and
b2OLS.
16

17.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Yn
Y1
X1
Xn
X
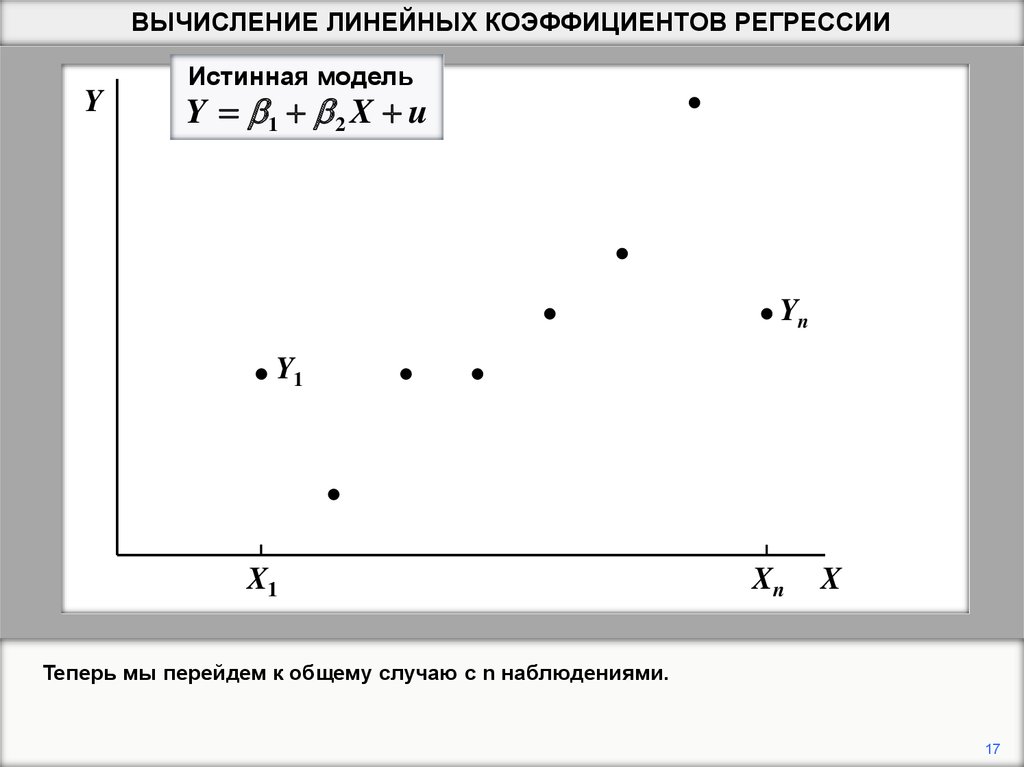
Теперь мы перейдем к общему случаю с n наблюдениями.
17

18.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
b1
b2
Yˆ1 b1 b2 X 1
X1
Xn
X
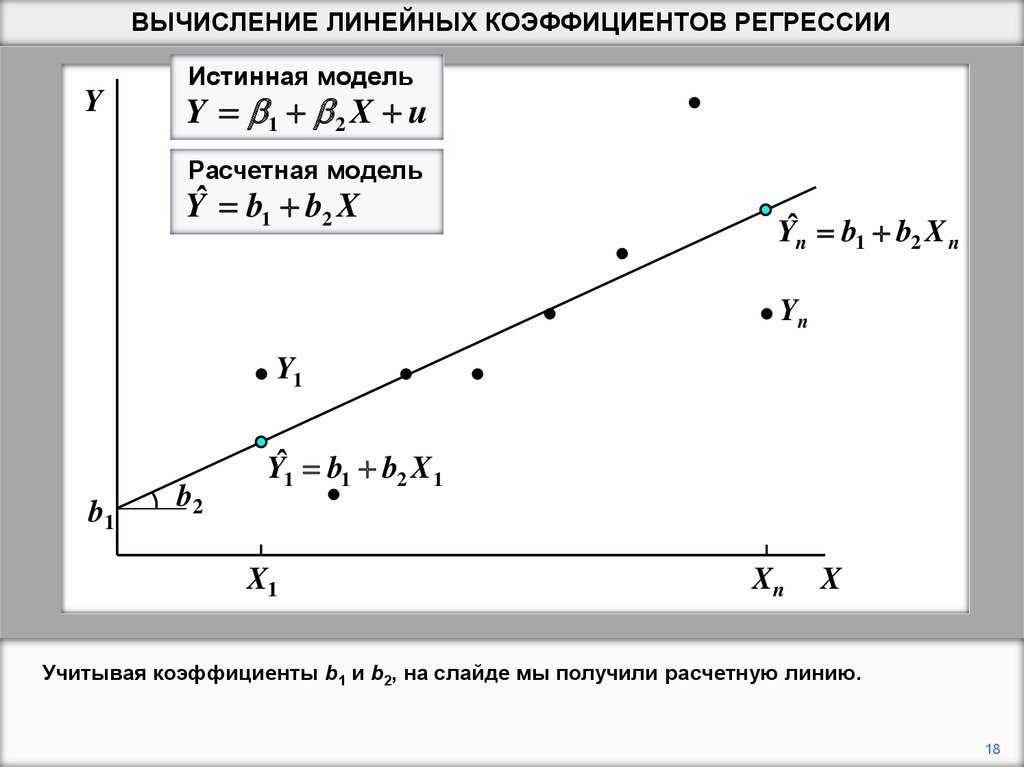
Учитывая коэффициенты b1 и b2, на слайде мы получили расчетную линию.
18

19.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
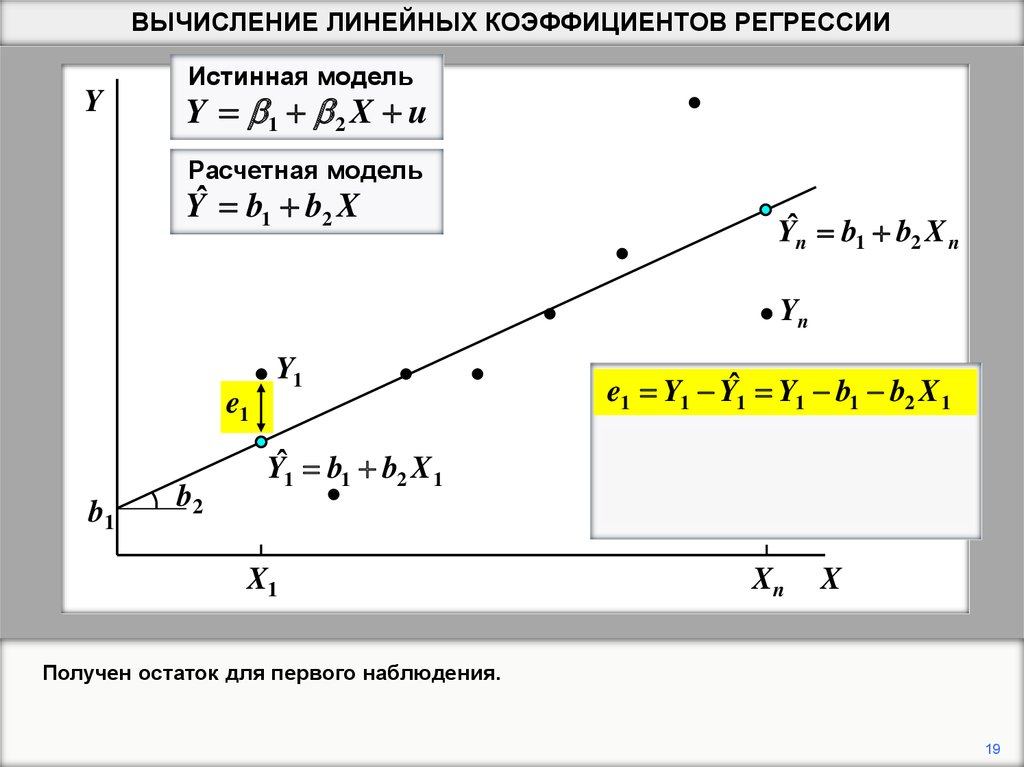
e1 Y1 Yˆ1 Y1 b1 b2 X 1
Yˆ1 b1 b2 X 1
.....
e1
b1
b2
X1
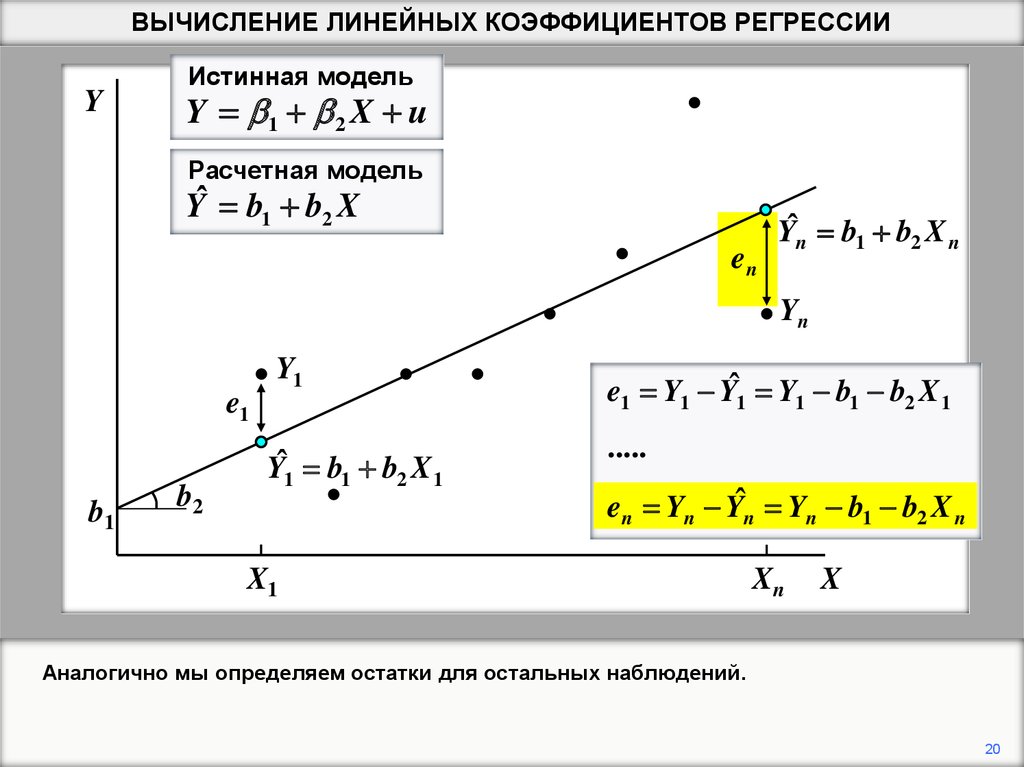
en Yn Yˆn Yn b1 b2 X n
Xn
X
Получен остаток для первого наблюдения.
19

20.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
en
Yˆn b1 b2 X n
Yn
Y1
e1 Y1 Yˆ1 Y1 b1 b2 X 1
Yˆ1 b1 b2 X 1
.....
e1
b1
b2
en Yn Yˆn Yn b1 b2 X n
X1
Xn
X
Аналогично мы определяем остатки для остальных наблюдений.
20

21.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS e12 ... en2 (Y1 b1 b2 X 1 ) 2 ... (Yn b1 b2 X n ) 2
Y12 b12
...
b22 X 12
2b1Y1
2b2 X 1Y1
2b1b2 X 1
b22 X n2
2b1Yn
2b2 X nYn
2b1b2 X n
Yn2 b12
Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS, сумма квадратов остатков, определена для общего случая. Для сравнения
приведены данные численного примера.
21

22.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS e12 ... en2 (Y1 b1 b2 X 1 ) 2 ... (Yn b1 b2 X n ) 2
Y12 b12
...
b22 X 12
2b1Y1
2b2 X 1Y1
2b1b2 X 1
b22 X n2
2b1Yn
2b2 X nYn
2b1b2 X n
Yn2 b12
Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
Раскрываем скобки, возведя соответствующие выражения в квадрат.
22

23.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS e12 e22 e32 ( 3 b1 b2 ) 2 (5 b1 2b2 ) 2 (6 b1 3b2 ) 2
9 b12
b22 6b1 6b2 2b1b2
25 b12 4b22 10b1 20b2 4b1b2
36 b12 9b22 12b1 36b2 6b1b2
70 3b12 14b22 28b1 62b2 12b1b2
RSS e12 ... en2 (Y1 b1 b2 X 1 ) 2 ... (Yn b1 b2 X n ) 2
Y12 b12
...
b22 X 12
2b1Y1
2b2 X 1Y1
2b1b2 X 1
b22 X n2
2b1Yn
2b2 X nYn
2b1b2 X n
Yn2 b12
Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
Приводим подобные члены.
23

24.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
В этом уравнении наблюдения по X и Y являются просто данными, которые
определяют коэффициенты в выражении для RSS.
24

25.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
Переменными в уравнении для RSS являются b1 и b2. Обычно b1 and b2 являются
константами, а X и Y - переменными.
25

26.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
Если есть сомнения, то можно сравнить общий случай с нашим конкретным
примером.
26

27.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS
0 2nb1 2 Yi 2b2 X i 0
b1
Первая производная по b1.
27

28.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS
0 2nb1 2 Yi 2b2 X i 0
b1
nb1 Yi b2 X i
b1 Y b2 X
Получаем окончательное выражение для b1 .
28

29.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS 70 3b12 14b22 28b1 62b2 12b1b2
RSS
0 6b1 12b2 28 0
b1
} b1 1.67, b2 1.50
RSS
0 12b1 28b2 62 0
b2
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS
0 2nb1 2 Yi 2b2 X i 0
b1
nb1 Yi b2 X i
b1 Y b2 X
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
Первая производная по b2.
29

30.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
b2 X i2 X iYi b1 X i 0
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS
0 2nb1 2 Yi 2b2 X i 0
b1
nb1 Yi b2 X i
b1 Y b2 X
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
Разделим на 2.
30

31.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
b2 X i2 X iYi b1 X i 0
b2 X i2 X iYi (Y b2 X ) X i 0
RSS Yi 2 nb12 b22 X i2 2b1 Yi 2b2 X iYi 2b1b2 X i
RSS
0 2nb1 2 Yi 2b2 X i 0
b1
nb1 Yi b2 X i
b1 Y b2 X
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
Теперь заменим b1 на выражение, полученное для него, и получим уравнение для b2.
31

32.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
b2 X i2 X iYi b1 X i 0
b2 X i2 X iYi (Y b2 X ) X i 0
b2 X i2 X iYi (Y b2 X )nX 0
X
X
i
n
X
i
nX
Используем определение среднего значения выборки.
32

33.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
b2 X i2 X iYi b1 X i 0
b2 X i2 X iYi (Y b2 X ) X i 0
b2 X i2 X iYi (Y b2 X )nX 0
b2 X i2 X iYi nXY nb2 X 2 0
Раскрыты скобки в третьем слагаемом.
33

34.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
RSS
0 2b2 X i2 2 X iYi 2b1 X i 0
b2
b2 X i2 X iYi b1 X i 0
b2 X i2 X iYi (Y b2 X ) X i 0
b2 X i2 X iYi (Y b2 X )nX 0
b2 X i2 X iYi nXY nb2 X 2 0
b2 X i2 nX 2 X iYi nXY
В правой части остались слагаемые, не зависимые от b2 .
34

35.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2 X i2 nX 2 X iYi nXY
Запишем наш результат в новый слайд.
35

36.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
X Y nXY
X nX
i
i
2
i
2
Получаем выражение для b2.
36

37.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
На практике мы будем использовать альтернативное выражение. Мы
продемонстрируем, что они эквивалентны.
37

38.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
X
i
X Yi Y X iYi X iY XYi XY
X iYi Y X i X Yi nXY
X iYi Y nX X nY nXY
X iYi nXY
Раскрываем скобки в числителе.
38

39.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
X
i
X Yi Y X iYi X iY XYi XY
X iYi Y X i X Yi nXY
X iYi Y nX X nY nXY
X iYi nXY
Упрощаем числитель далее.
39

40.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
X
X
X
i
X Yi Y X iYi X iY XYi XY
i
n
X
i
nX
X iYi Y X i X Yi nXY
X iYi Y nX X nY nXY
X iYi nXY
Упрощаем далее.
40

41.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
X
i
X Yi Y X iYi X iY XYi XY
X iYi Y X i X Yi nXY
X iYi Y nX X nY nXY
X iYi nXY
Мы показали, что числители двух выражений одинаковы.
41

42.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
b2 X i2 nX 2 X iYi nXY
b2
b2
X Y nXY
X nX
X X Y Y
X X
i
i
2
i
2
i
i
2
i
X
i
X Yi Y X iYi nXY
2
2
2
X
X
X
n
X
i
i
Знаменатели являются эквивалентными выражениями.
42

43.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
b1
b2
Yˆ1 b1 b2 X 1
X1
Xn
X
Подведем итог тому, что мы сделали.
43

44.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
b1
b2
Yˆ1 b1 b2 X 1
b1 Y b2 X
b2
X X Y Y
X X
i
i
2
i
X1
Xn
X
Мы нашли параметры расчетной линии, минимизируя сумму квадратов остатков. В
результате мы получили выражения для b1 и b2.
44

45.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
b1
b2
Yˆ1 b1 b2 X 1
b1OLS Y b2OLS X
OLS
2
b
X X Y Y
X X
i
i
2
i
X1
Xn
X
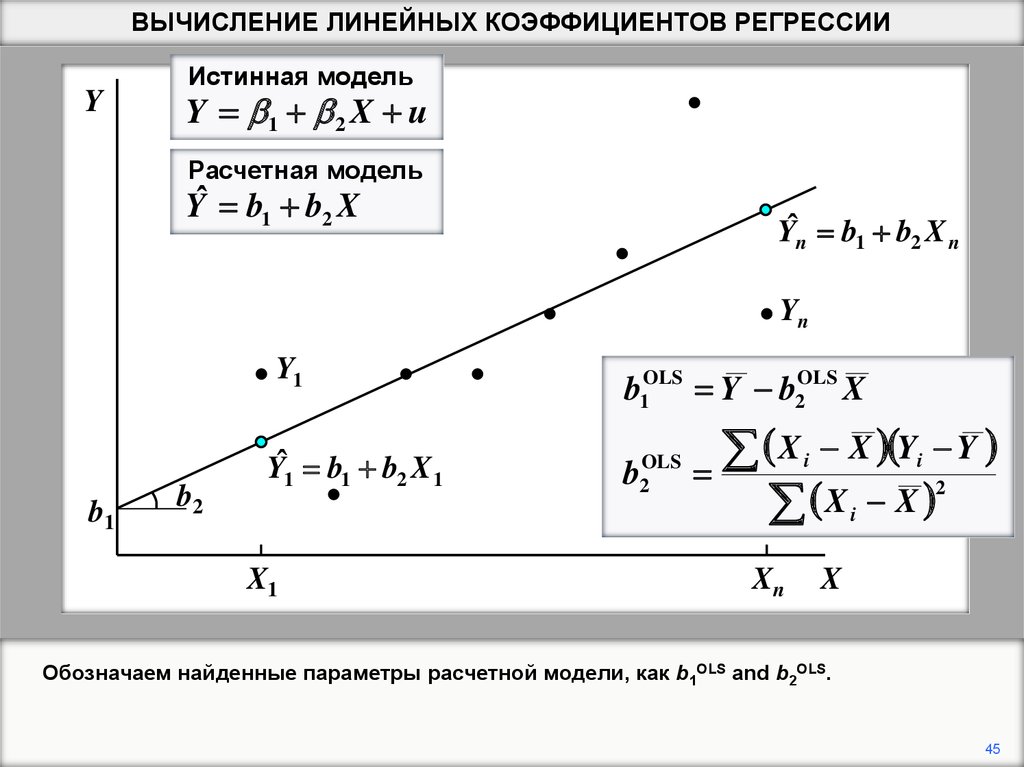
Обозначаем найденные параметры расчетной модели, как b1OLS and b2OLS.
45

46.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Y
Истинная модель
Y 1 2 X u
Расчетная модель
Yˆ b1 b2 X
Yˆn b1 b2 X n
Yn
Y1
b1
b2
Yˆ1 b1 b2 X 1
b1OLS Y b2OLS X
OLS
2
b
X X Y Y
X X
i
i
2
i
X1
Xn
X
В дальнейшем мы будем, как правило, пользоваться оценками OLS, и поэтому
надстрочную надпись «OLS» мы использовать не будем.
46

47.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y 2 X u
Расчетная модель
Yˆ b2 X
В случае простой регрессионной модели истинная и расчетная модели записываются
без свободного члена.
47

48.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y 2 X u
Расчетная модель
Yˆ b2 X
ei Yi Yˆi Yi b2 X i
Мы выведем выражение для b2, используя критерий наименьших квадратов. Остаток
в наблюдении i равен ei = Yi – b2Xi.
48

49.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Y 2 X u
Расчетная модель
Yˆ b2 X
ei Yi Yˆi Yi b2 X i
RSS Yi b2 X i Yi 2 2b2 X iYi b22 X i2
2
Здесь мы получаем выражение для суммы квадратов остатков.
49

50.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Расчетная модель
Y 2 X u
Yˆ b2 X
ei Yi Yˆi Yi b2 X i
RSS Yi b2 X i Yi 2 2b2 X iYi b22 X i2
2
dRSS
2b2 X i2 2 X iYi
db2
2b2OLS X i2 2 X iYi 0
Продифференцируем по b2.
50

51.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Расчетная модель
Yˆ b2 X
Y 2 X u
ei Yi Yˆi Yi b2 X i
RSS Yi b2 X i Yi 2 2b2 X iYi b22 X i2
2
dRSS
2b2 X i2 2 X iYi
db2
2b2OLS X i2 2 X iYi 0
OLS
2
b
XY
X
i
i
2
i
Следовательно, мы получаем оценку OLS для b2 для этой модели.
51

52.

ВЫЧИСЛЕНИЕ ЛИНЕЙНЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Истинная модель
Расчетная модель
Yˆ b2 X
Y 2 X u
ei Yi Yˆi Yi b2 X i
RSS Yi b2 X i Yi 2 2b2 X iYi b22 X i2
2
dRSS
2b2 X i2 2 X iYi
db2
2b2OLS X i2 2 X iYi 0
OLS
2
b
XY
X
i
i
2
i
d 2 RSS
2
2
X
i 0
2
db2
Вторая производная положительна, подтверждая, что мы нашли минимум.
52

English Русский Rules