Similar presentations:
F-тест на качество оценивания
1.
F-тест на качество оцениванияМодель
Y = b 1 + b 2X + u
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
В более ранней последовательности было показано, что сумма квадратов фактических
значений Y (TSS: общая сумма квадратов) может быть разложена на сумму квадратов
установленных значений (ESS: объясненная сумма квадратов) и сумма квадратов остатков.
1
2.
F КРИТЕРИЙ ПРИГОДНОСТИМодель
Y = b 1 + b 2X + u
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
R2, обычная мера критерия пригодности, тогда определялось как отношение
объясненной суммы квадратов к общей сумме квадратов.
2
3.
F КРИТЕРИЙ ПРИГОДНОСТИМодель
Y = b 1 + b 2X + u
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
Нулевая гипотеза, которую мы собираемся протестировать, заключается в том, что
модель не имеет объясняющей силы.
3
4.
F КРИТЕРИЙ ПРИГОДНОСТИY = b 1 + b 2X + u
Модель
Нулевая гипотеза: :
H0 : b 2 = 0
Альтернативная гипотеза :
H1: b 2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
Так как X является единственной объясняющей переменной на данный момент,
нулевая гипотеза состоит в том, что Y не определяется X. Математически мы имеем H0:
b2 = 0
4
5.
F КРИТЕРИЙ ПРИГОДНОСТИМодель
Y = b 1 + b 2X + u
Нулевая гипотеза :
H0 : b 2 = 0
Альтернативная гипотеза : H1:
b2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
Гипотезы, касающиеся хорошего соответствия, проверяются по статистике F, как показано. k
- количество параметров в уравнении регрессии, которое в настоящее время составляет
всего 2
5
6.
F КРИТЕРИЙ ПРИГОДНОСТИY = b 1 + b 2X + u
Модель
Нулевая гипотеза:
Альтернативная гипотеза :
H0 : b 2 = 0
H1: b 2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
n - k, как и в t-статистике, число степеней свободы (количество наблюдений за
вычетом количества оцениваемых параметров). Для простого регрессионного анализа
это n -2.
6
7.
F КРИТЕРИЙ ПРИГОДНОСТИМодель
Y = b 1 + b 2X + u
Нулевая гипотеза:
H0 : b 2 = 0
Альтернативная гипотеза : H1:
b2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
В качестве альтернативы F-статистика может быть записана в терминах R2. Сначала
разделите числитель и знаменатель на TSS
7
8.
F КРИТЕРИЙ ПРИГОДНОСТИМодель
Y = b 1 + b 2X + u
Нулевая гипотеза:
H0 : b 2 = 0
Альтернативная гипотеза :
H1: b 2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
Теперь мы можем переписать статистику F, как показано. R2 в числителе прямо
вытекает из определения R2.
8
9.
F КРИТЕРИЙ ПРИГОДНОСТИRSS TSS ESS
ESS
1
1 R2
TSS
TSS
TSS
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
Легко продемонстрировано, что RSS / TSS равно 1 – R2.
9
10.
F КРИТЕРИЙ ПРИГОДНОСТИY = b 1 + b 2X + u
Модель
Нулевая гипотеза:
H0 : b 2 = 0
Альтернативная гипотеза: H1:
b2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
F - монотонно возрастающая функция R2. С ростом R2 числитель увеличивается, а
знаменатель уменьшается, поэтому по обеим причинам F увеличивается
10
11.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
80
60
40
20
0
0
0.2
0.4
0.6
0.8
1
R2
Здесь F изображается как функция R2 для случая, когда имеется 1 поясняющая
переменная и 20 наблюдений. Поскольку k = 2, n – k = 18. H0
11
12.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
80
60
40
20
0
0
0.2
0.4
0.6
0.8
1
R2
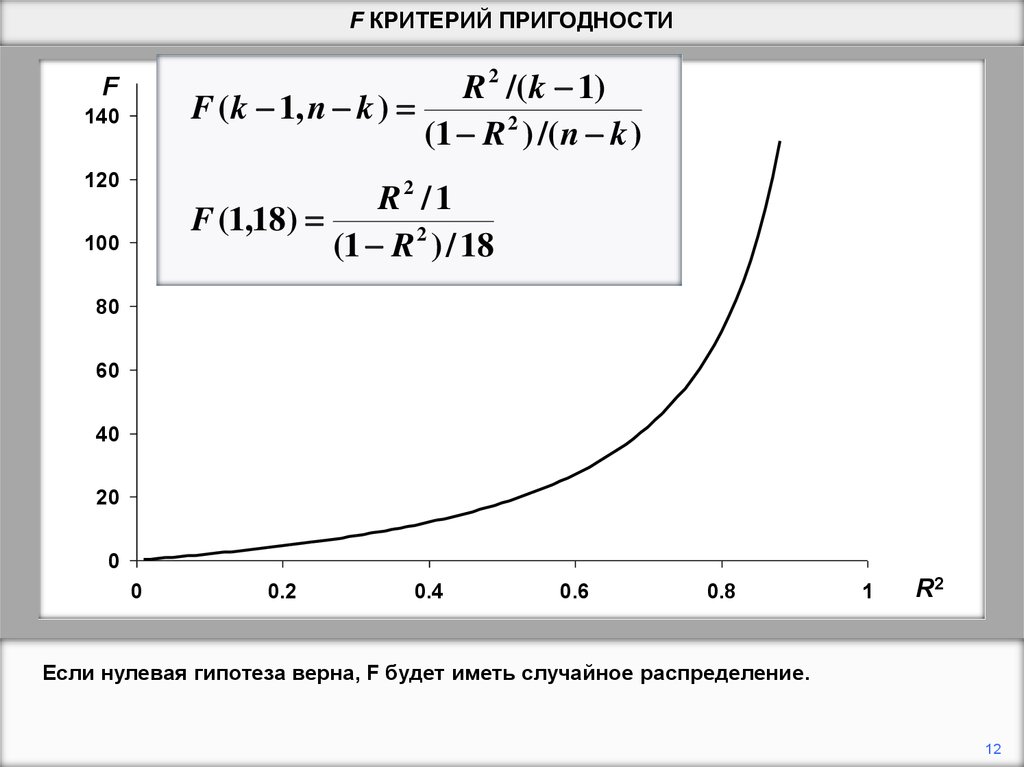
Если нулевая гипотеза верна, F будет иметь случайное распределение.
12
13.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
80
60
40
20
0
0
0.2
0.4
0.6
0.8
1
R2
Будет некоторая критическая ценность, которая будет превалировать, как
случайность, всего в 5 процентах случаев. Если мы выполняем 5-процентный тест
значимости, мы отклоним H0 ,если статистика F больше этого критического значения.
13
14.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
80
60
40
20
4.41
0
0
0.2
0.4
0.6
0.8
1
R2
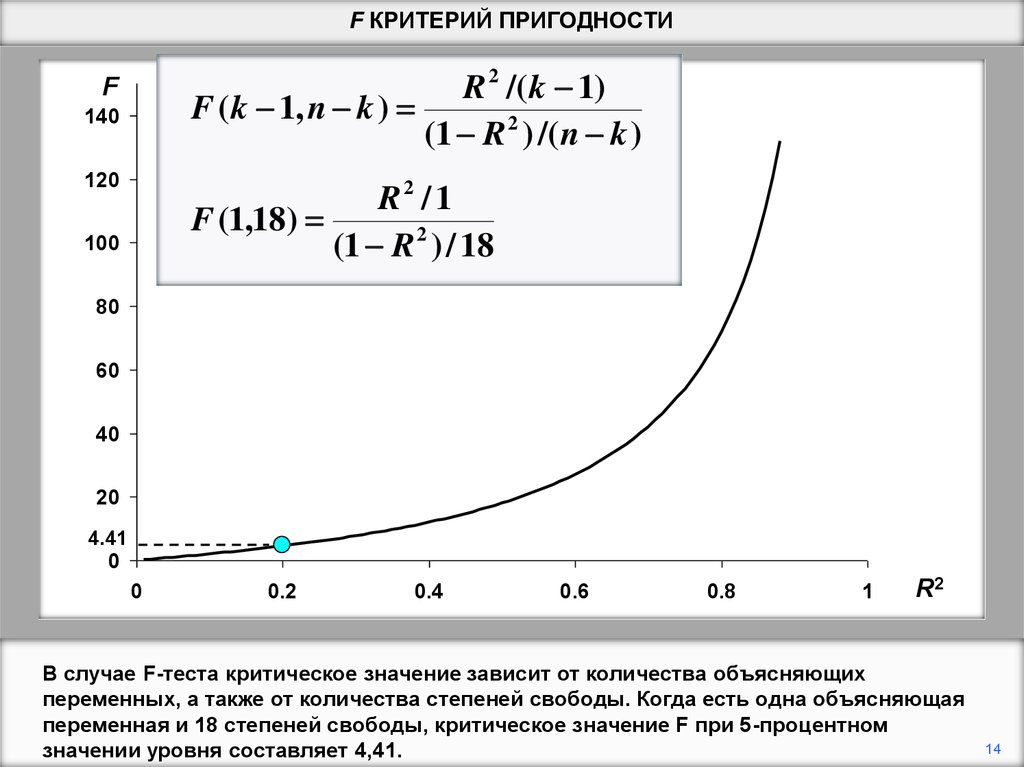
В случае F-теста критическое значение зависит от количества объясняющих
переменных, а также от количества степеней свободы. Когда есть одна объясняющая
переменная и 18 степеней свободы, критическое значение F при 5-процентном
значении уровня составляет 4,41.
14
15.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,5% (1,18) 4.41
80
60
40
20
4.41
0
0
0.2
0.4
0.6
0.8
1
R2
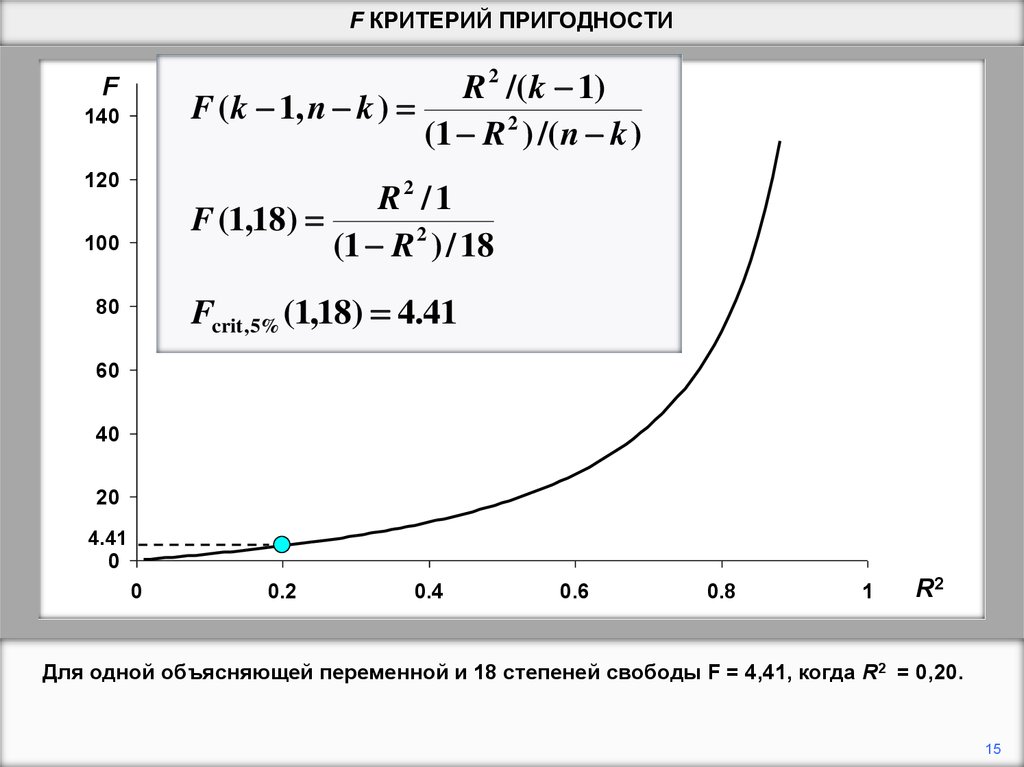
Для одной объясняющей переменной и 18 степеней свободы F = 4,41, когда R2 = 0,20.
15
16.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,5% (1,18) 4.41
80
60
40
20
4.41
0
0
0.2
0.4
0.6
0.8
1
R2
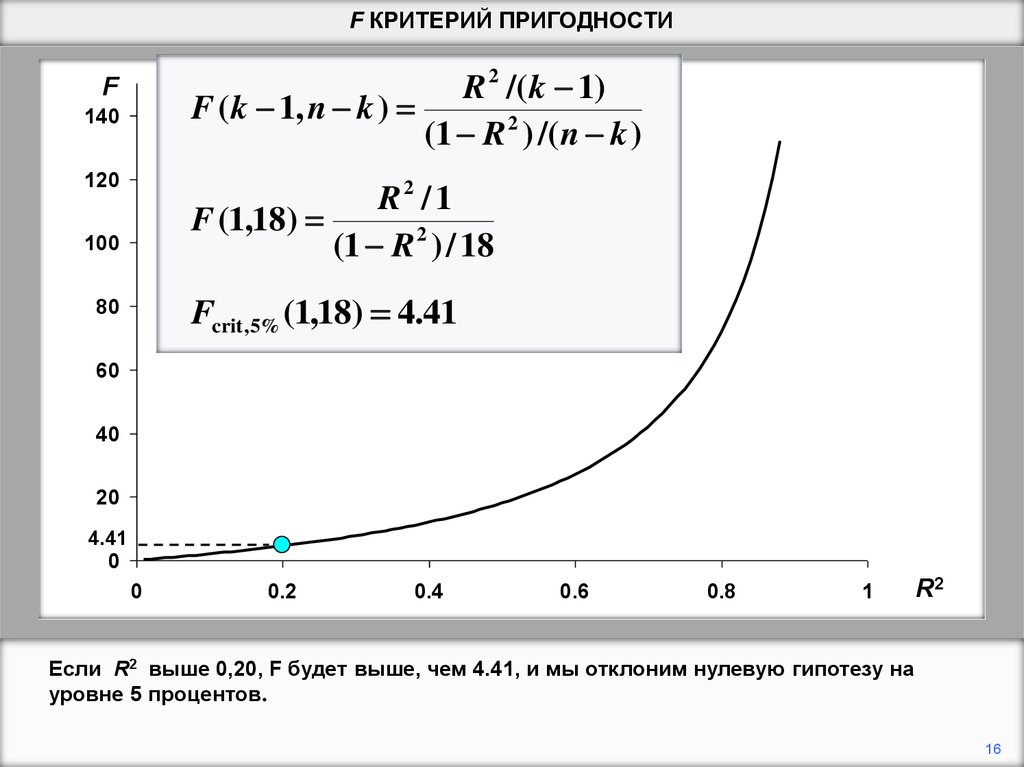
Если R2 выше 0,20, F будет выше, чем 4.41, и мы отклоним нулевую гипотезу на
уровне 5 процентов.
16
17.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,1% (1,18) 8.29
80
60
40
20
8.29
0
0
0.2
0.32
0.4
0.6
0.8
1
R2
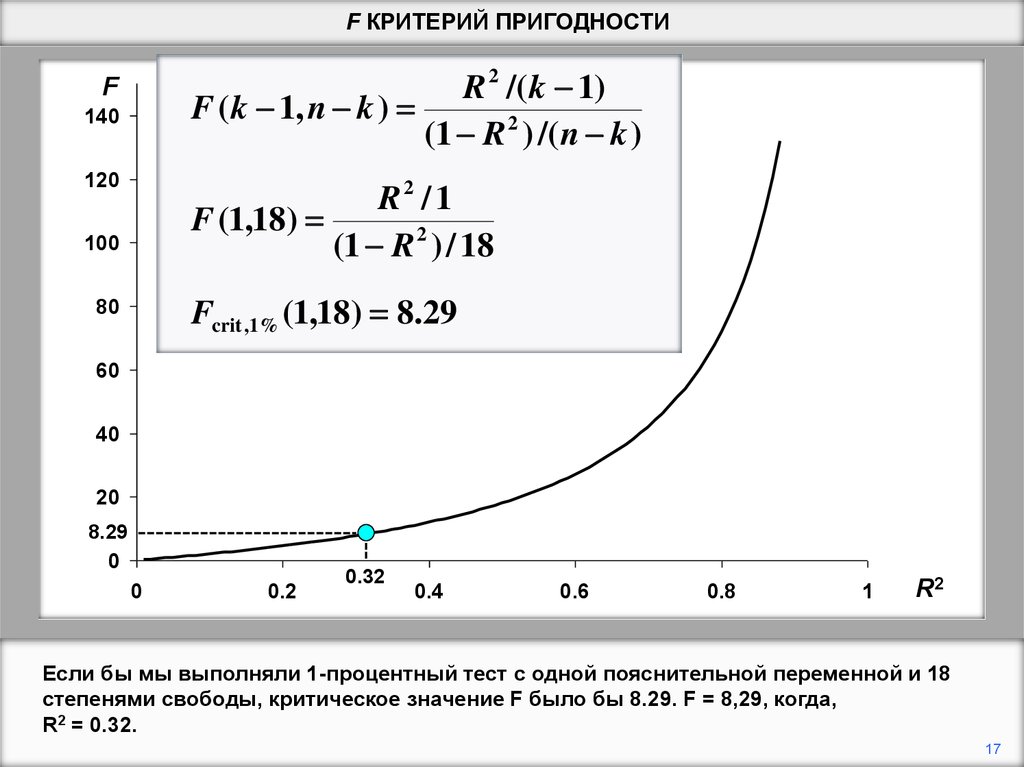
Если бы мы выполняли 1-процентный тест с одной пояснительной переменной и 18
степенями свободы, критическое значение F было бы 8.29. F = 8,29, когда,
R2 = 0.32.
17
18.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,1% (1,18) 8.29
80
60
40
20
8.29
0
0
0.2
0.32
0.4
0.6
0.8
1
R2
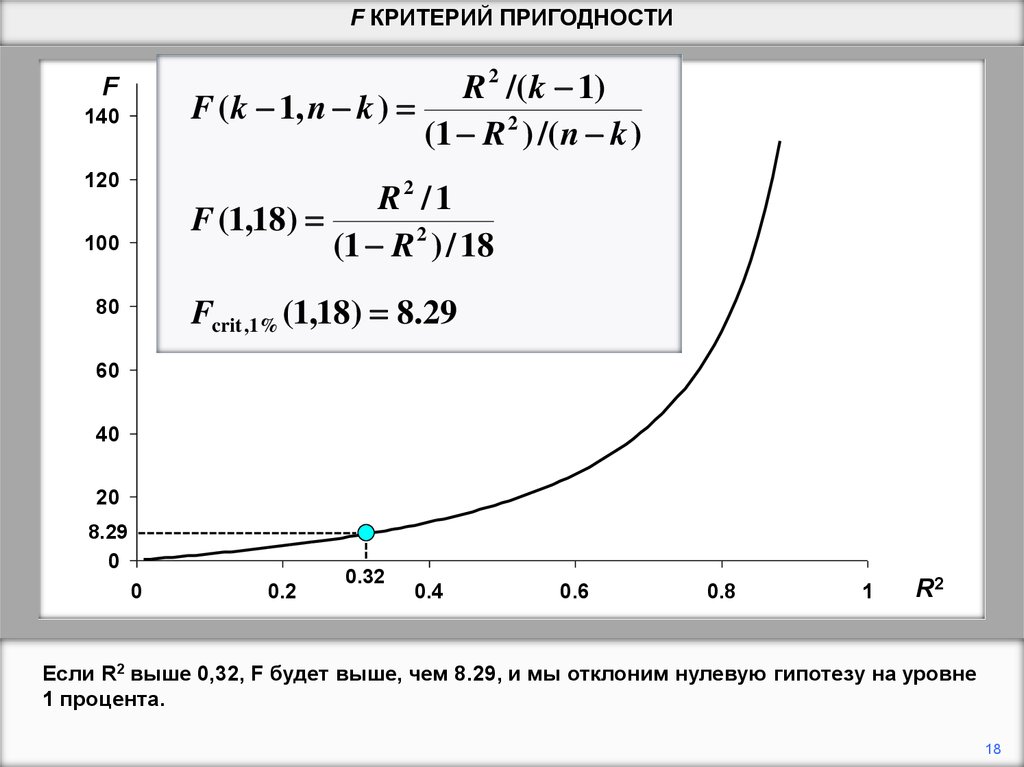
Если R2 выше 0,32, F будет выше, чем 8.29, и мы отклоним нулевую гипотезу на уровне
1 процента.
18
19.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,1% (1,18) 8.29
80
60
40
20
8.29
0
0
0.2
0.32
0.4
0.6
0.8
1
R2
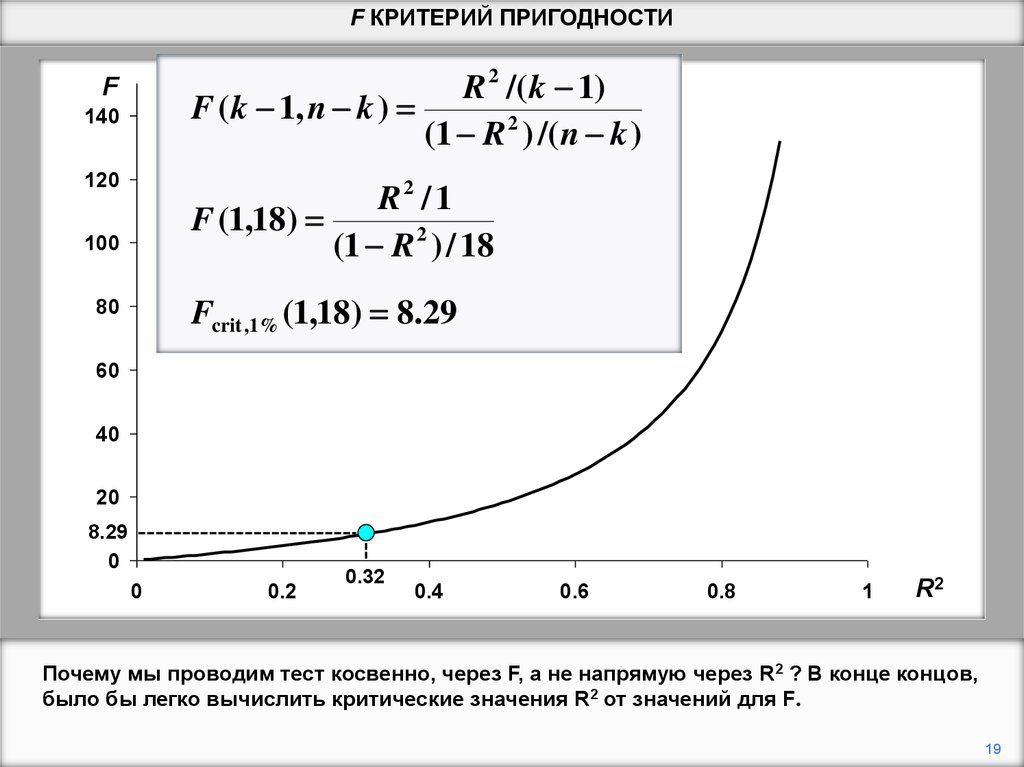
Почему мы проводим тест косвенно, через F, а не напрямую через R2 ? В конце концов,
было бы легко вычислить критические значения R2 от значений для F.
19
20.
F КРИТЕРИЙ ПРИГОДНОСТИR 2 /( k 1)
F ( k 1, n k )
(1 R 2 ) /( n k )
F
140
120
R2 / 1
F (1,18)
(1 R 2 ) / 18
100
Fcrit ,1% (1,18) 8.29
80
60
40
20
8.29
0
0
0.2
0.32
0.4
0.6
0.8
1
R2
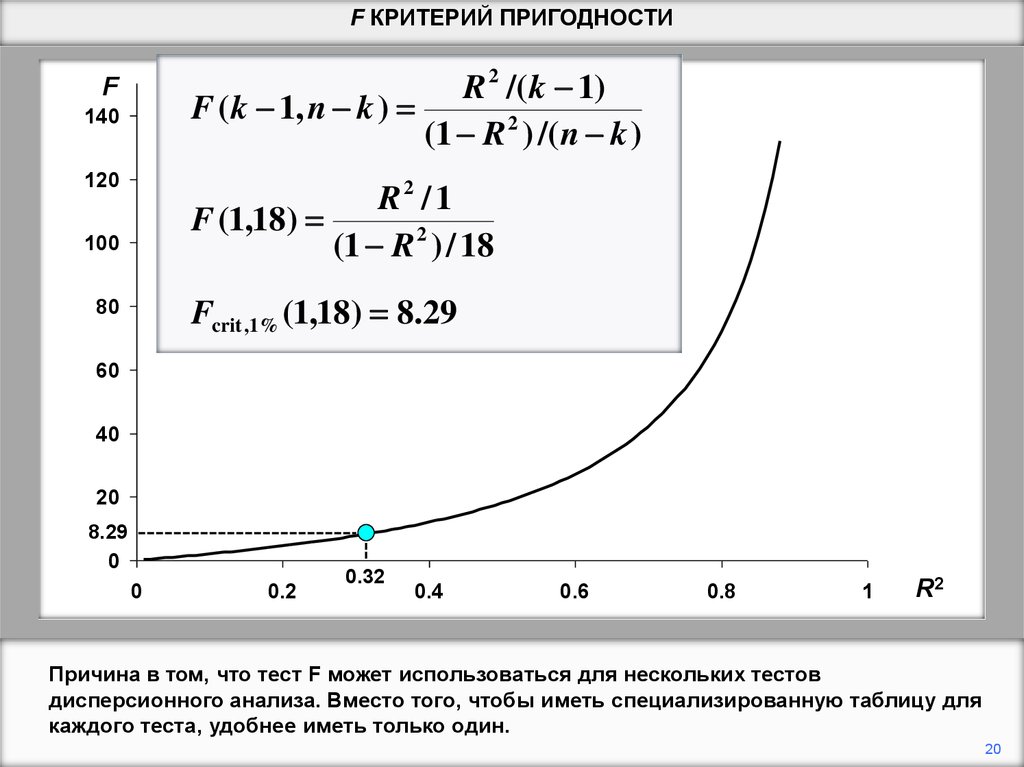
Причина в том, что тест F может использоваться для нескольких тестов
дисперсионного анализа. Вместо того, чтобы иметь специализированную таблицу для
каждого теста, удобнее иметь только один.
20
21.
F КРИТЕРИЙ ПРИГОДНОСТИY = b 1 + b 2X + u
Модель
Нулевая гипотеза:
H0 : b 2 = 0
Альтернативная гипотеза: H1:
b2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
Обратите внимание, что для простого регрессионного анализа нулевые и
альтернативные гипотезы математически точно такие же, как для двухстороннего tтеста. Может ли тест F прийти к другому выводу из t-теста?
21
22.
F КРИТЕРИЙ ПРИГОДНОСТИY = b 1 + b 2X + u
Модель
Нулевая гипотеза:
H0 : b 2 = 0
Альтернативная гипотеза: H1:
b2 ≠ 0
2
2
2
ˆ
(
Y
Y
)
(
Y
Y
)
e
TSS ESS RSS
2
ˆ
(
Y
Y
)
ESS
i
R2
TSS (Yi Y )2
ESS
( k 1)
ESS /( k 1) TSS
R 2 /( k 1)
F ( k 1, n k )
RSS /( n k ) RSS ( n k ) (1 R 2 ) /( n k )
TSS
Ответ, конечно, нет. Мы продемонстрируем, что для простого регрессионного анализа
статистика F является квадратом статистики t.
22
23.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того, что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Начнем с замены ESS и RSS их математическими выражениями.
23
24.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того, что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Знаменатель представляет собой выражение для su2, оценщика su2, для простой
модели регрессии. Разбиваем числитель, используя выражение для установленного
соотношения.
24
25.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,что F= t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Члены b1 в числителе отменяют. Остальные числители могут быть сгруппированы,
как показано.
25
26.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Мы берем член b22 из суммирования как фактор.
26
27.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
We move the term involving X to the denominator.
27
28.
F Критерий пригодностиДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Знаменатель представляет собой квадрат стандартной ошибки b2.
28
29.
F Критерий пригодностиДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Отсюда получаем b22 деленный на квадрат стандартной ошибки b2. Это t статистика,
квадрат.
29
30.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Можно также показать, что критическое значение F на любом уровне значимости равно
квадрату критического значения t. Мы не будем пытаться это доказать H0
30
31.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,что F = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Поскольку тест F эквивалентен двухстороннему t-критерию в простой модели
регрессии, нет смысла выполнять оба теста. Фактически, если это оправдано,
односторонний t-тест будет лучше, чем либо потому, что он более мощный (более
низкий риск ошибки типа II, если H0 является ложным)
31
32.
F КРИТЕРИЙ ПРИГОДНОСТИДемонстрация того,чтоF = t2
2
ˆ
Yi Y
ESS
F
RSS /( n 2) ei2 n 2
2
[
b
b
X
]
[
b
b
X
]
1 2 i 1 2
su2
b22
2
2 Xi X 2
su
su
1
2
2 b22 X i X
su
b22
b22
2
t
2
2
X
X
s
.
e
.(
b
)
i
2
Тест F будет играть свою роль, когда мы придем к множественному регрессионному
анализу.
32
33.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
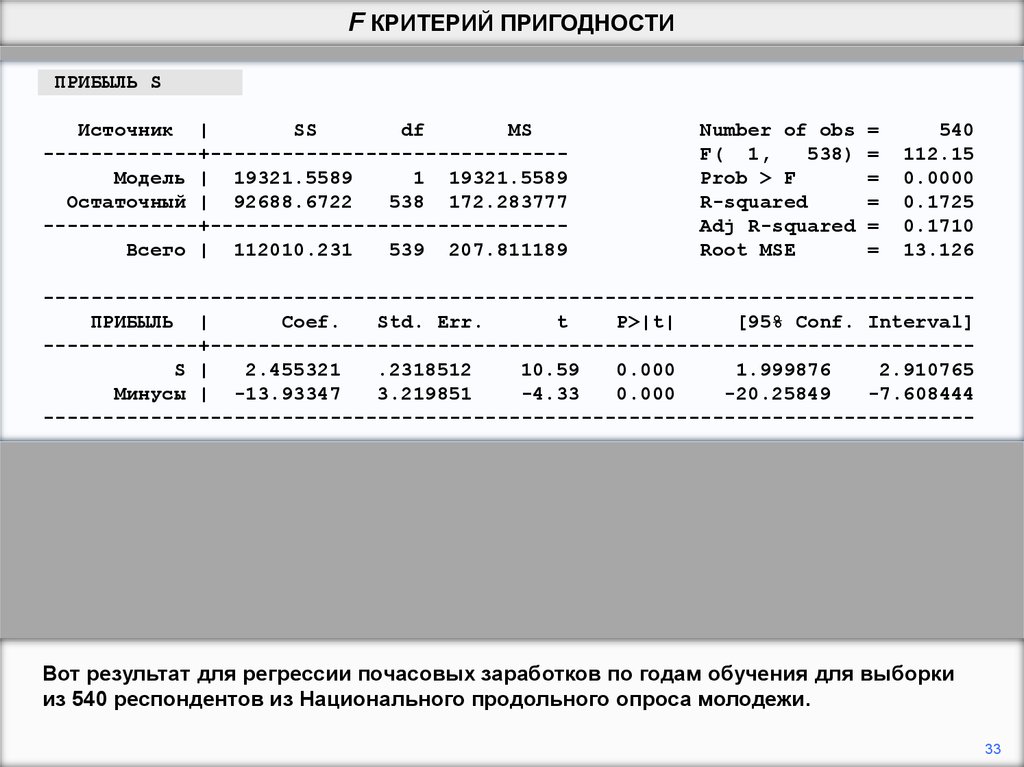
Вот результат для регрессии почасовых заработков по годам обучения для выборки
из 540 респондентов из Национального продольного опроса молодежи.
33
34.
F КРИТЕРИЙ ПРИГОДНОСТИПрибыль S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------Прибыль |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы| -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS
19322
19322
F 1, n 2
112.15
RSS / n 2 92689 / 540 2 172.28
Мы проверим, что статистика F была рассчитана правильно. Объясненная сумма
квадратов (описанная в Stata как модельная сумма квадратов) является 19322.
34
35.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы| -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS
19322
19322
F 1, n 2
112.15
RSS / n 2 92689 / 540 2 172.28
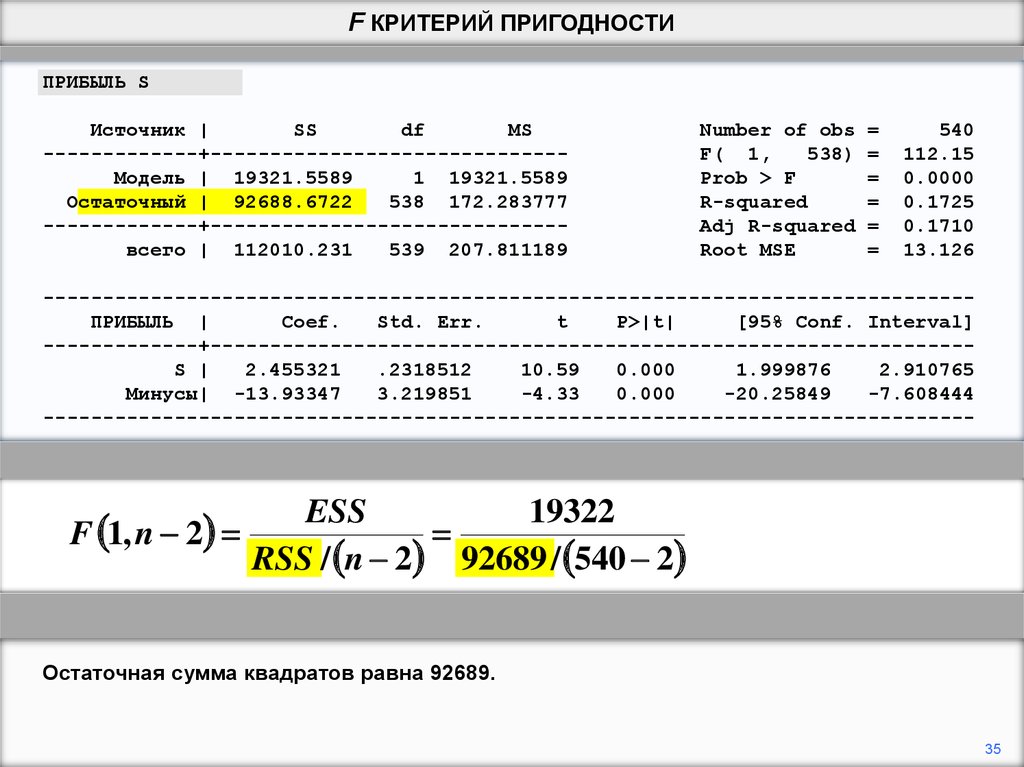
Остаточная сумма квадратов равна 92689.
35
36.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS
19322
19322
F 1, n 2
112.15
RSS / n 2 92689 / 540 2 172.28
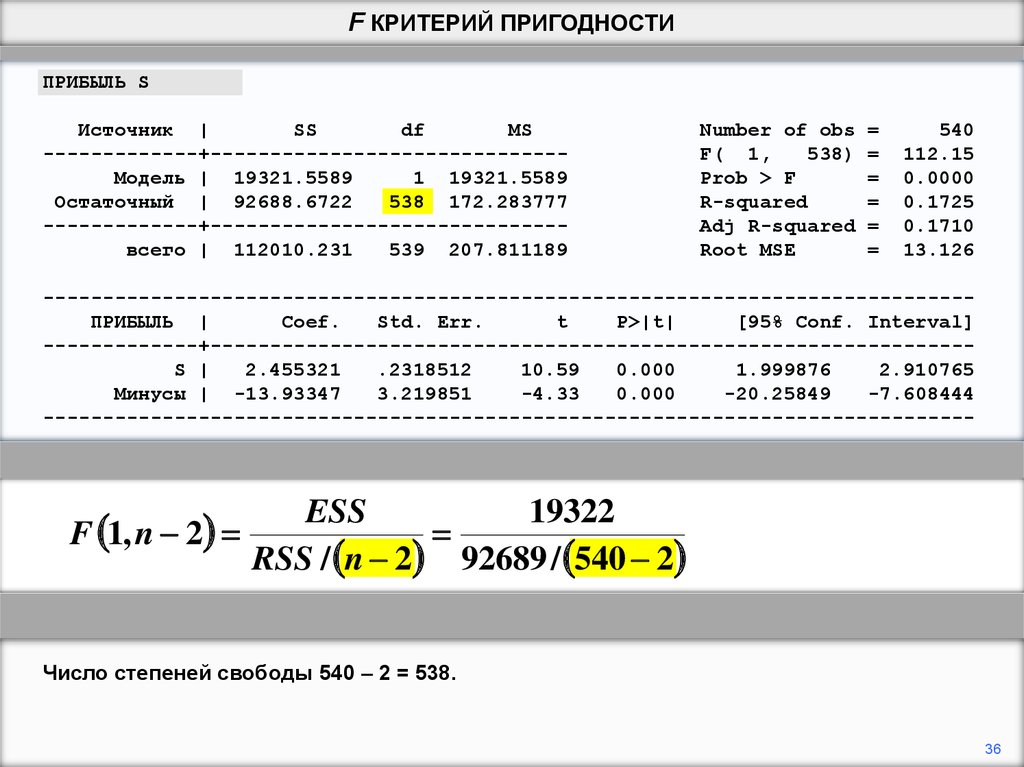
Число степеней свободы 540 – 2 = 538.
36
37.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ
S
Источник |
SS
df
MS
-------------+-----------------------------Модель
| 19321.5589
1 19321.5589
Остаточный
| 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS
19322
19322
F 1, n 2
112.15
RSS / n 2 92689 / 540 2 172.28
Знаменатель выражения для F, следовательно, 172,28. Заметим, что это оценка su2. Его
квадратный корень, обозначенный в Stata Root MSE, является оценкой стандартного
отклонения u.
37
38.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
ESS
19322
19322
F 1, n 2
112.15
RSS / n 2 92689 / 540 2 172.28
Наш расчет F согласуется с тем, что на выходе Stata.
38
39.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ
S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы| -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
R2
0.1725
F 1, n 2
112.15
2
1 R / n 2 1 0.1725 / 540 2
Мы также проверим статистику F, используя выражение для нее в терминах R2. Мы
снова видим, что он согласен.
39
40.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы| -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
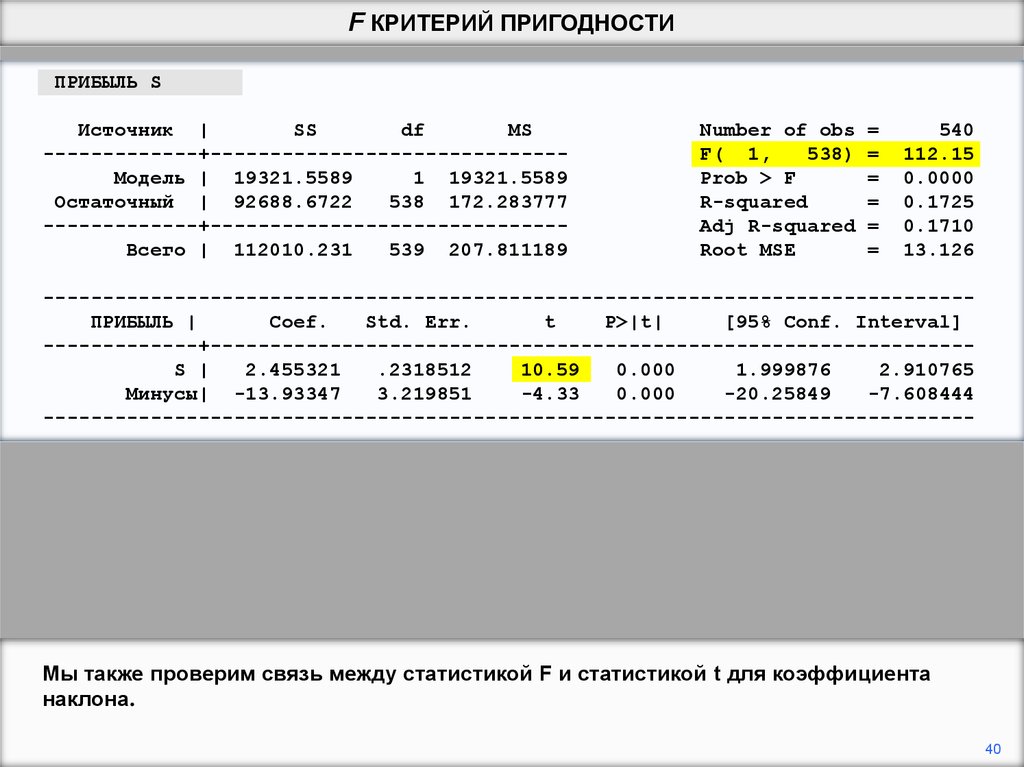
Мы также проверим связь между статистикой F и статистикой t для коэффициента
наклона.
40
41.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
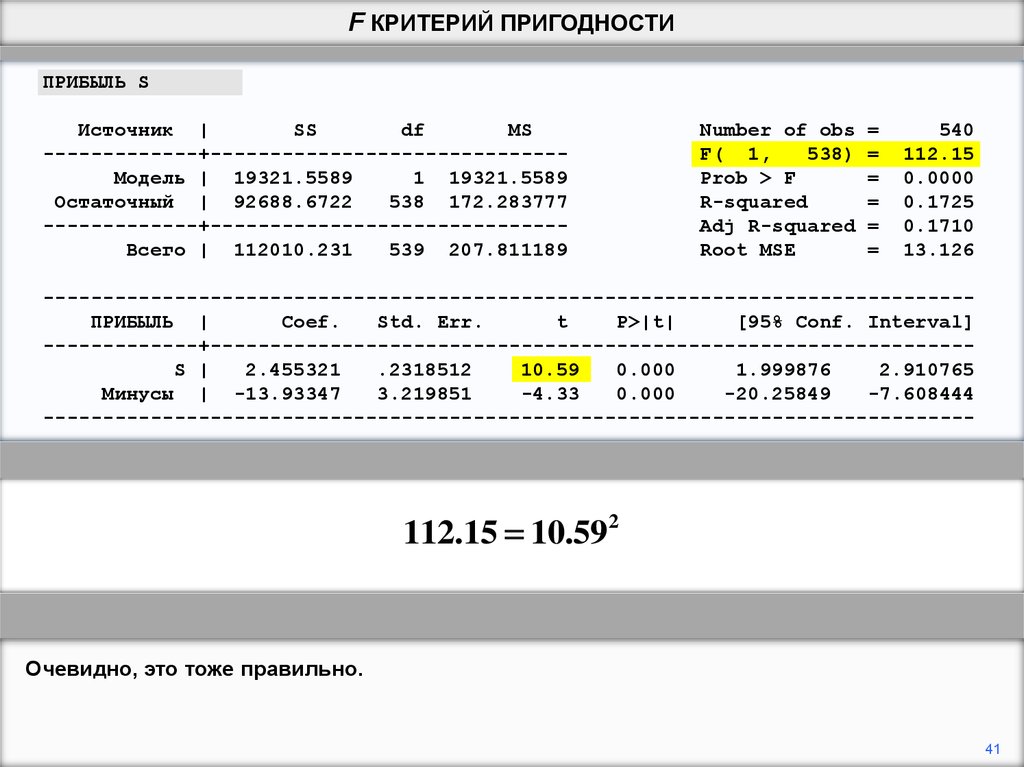
112.15 10.592
Очевидно, это тоже правильно.
41
42.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------ПРИБЫЛЬ |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
Fcrit, 0.1% 1,500 10.96
t crit, 0.1% 500 3.31
10.96 3.312
И критическое значение F является квадратом критического значения t. (Мы
используем значения для 500 степеней свободы, потому что те, для 538, не
отображаются в таблице.)
42
43.
F КРИТЕРИЙ ПРИГОДНОСТИПРИБЫЛЬ S
Источник |
SS
df
MS
-------------+-----------------------------Модель | 19321.5589
1 19321.5589
Остаточный | 92688.6722
538 172.283777
-------------+-----------------------------Всего | 112010.231
539 207.811189
Number of obs
F( 1,
538)
Prob > F
R-squared
Adj R-squared
Root MSE
=
=
=
=
=
=
540
112.15
0.0000
0.1725
0.1710
13.126
-----------------------------------------------------------------------------Прибыль |
Coef.
Std. Err.
t
P>|t|
[95% Conf. Interval]
-------------+---------------------------------------------------------------S |
2.455321
.2318512
10.59
0.000
1.999876
2.910765
Минусы | -13.93347
3.219851
-4.33
0.000
-20.25849
-7.608444
------------------------------------------------------------------------------
Fcrit, 0.1% 1,500 10.96
t crit, 0.1% 500 3.31
10.96 3.312
Отношения показаны для уровня значимости 0,1%, но, очевидно, это верно и для
любого другого уровня значимости.
43






























 mathematics
mathematics








