Similar presentations:
Проверка качества уравнения регрессии
1. Проверка качества уравнения регрессии
Лекция2. Цели лекции
Выполнимость теоретическихпредпосылок
Анализ расчетных статистических
показателей качества
Интерпретация регрессии
2
3. Случайные составляющие коэффициентов регрессии
После определения оценок b0 и b1 возникают вопросы:- насколько точно эмпирическое уравнение регрессии
соответствует уравнению для всей генеральной
совокупности;
- насколько близки оценки b0 и b1 к своим теоретическим
значениям 0 и 1;
- как близко оцененное значение y i к условному
математическому ожиданию M[Y/X = xi];
- насколько надежны найденные оценки.
Для ответа на эти вопросы необходимы дополнительные
исследования.
3
4. Свойства оценок коэффициентов регрессии
Оценки b0 и b1 представляют собой случайныевеличины, зависящие от случайного члена в
уравнении регрессии.
Рассмотрим теоретическую модель парной линейной
регрессии и ее оценку по выборке из n наблюдений:
Y 0 1 X
Справедлива формула:
Y b0 b1 X
b1
S xy
S x2
4
5. Свойства оценок коэффициентов регрессии
Представим выборочную ковариацию Sxy в виде:Sxy = Cov(X, 0+ 1X+ ) = Cov(X, 0) + Cov(X, 1X) + Cov(X, ) =
= 1Sx2 + Cov(X, ).
S xy
S x
Следовательно, b1 2 1 2 ,
Sx
Sx
где 1 постоянная составляющая;
компонента.
S x
S x2 случайная
Тот же результат можно получить и для коэффициента b0.
5
6. Свойства оценок коэффициентов регрессии
Т.о. показано, чтоСвойства оценок коэффициентов регрессии, а
следовательно, и качество построенного
уравнения регрессии существенно зависят от
свойств случайной составляющей.
6
7. Свойства оценок коэффициентов регрессии
Доказано, что для получения по МНК наилучшихрезультатов (при этом оценки bi обладают
свойствами состоятельности, несмещенности
и эффективности) необходимо выполнение
ряда предпосылок относительно случайного
отклонения.
7
8. Предпосылки использования МНК (условия Гаусса – Маркова)
10. Случайное отклонение имеет нулевоематематическое ожидание.
20. Дисперсия случайного отклонения постоянна.
30. Наблюдаемые значения случайных отклонений
независимы друг от друга.
40. Случайное отклонение д.б. независимо от объясняющей
переменной.
50. Регрессионная модель является линейной относительно
параметров, корректно специфицирована и содержит
аддитивный случайный член.
8
9. Предпосылки использования МНК (условия Гаусса – Маркова)
10. Случайное отклонение имеет нулевоематематическое ожидание.
M [ ] 0
Данное условие означает, что случайное
отклонение в среднем не оказывает влияния на
зависимую переменную.
9
10. Предпосылки использования МНК (условия Гаусса – Маркова)
20. Дисперсия случайного отклоненияпостоянна.
D[ ] const
2
Из данного условия следует, что несмотря на то, что при
каждом конкретном наблюдении случайное отклонение i
может быть различным, но не должно быть причин,
вызывающих большую ошибку.
10
11. Предпосылки использования МНК (условия Гаусса – Маркова)
30. Наблюдаемые значения случайныхотклонений независимы друг от друга.
i j
i j
0,
Cov( i , j ) 2
, i j
Если данное условие выполняется, то говорят об отсутствии
автокорреляции.
11
12. Предпосылки использования МНК (условия Гаусса – Маркова)
40. Случайное отклонение д.б. независимоот объясняющей переменной.
X Cov( i , X i ) 0
i
i
Это условие выполняется, если объясняющая переменная не
является случайной в данной модели.
12
13. Предпосылки использования МНК (условия Гаусса – Маркова)
50. Регрессионная модель являетсялинейной относительно параметров,
корректно специфицирована и содержит
аддитивный случайный член.
Yi 0 1 X i i
13
14. Предпосылки использования МНК (условия Гаусса – Маркова)
60. Наряду с выполнимостью указанных предпосылок припостроении линейных регрессионных моделей обычно
делаются еще некоторые предположения, а именно:
- случайное отклонение имеет нормальный закон
распределения;
- число наблюдений существенно больше числа
объясняющих переменных;
- отсутствуют ошибки спецификации;
- отсутствует линейная взаимосвязь между двумя или
несколькими объясняющими переменными.
14
15. Теорема Гаусса - Маркова
Теорема. Если предпосылки 10 – 50 выполнены, то оценки,полученные по МНК, обладают следующими свойствами:
1. Оценки являются несмещенными, т.е. M[b0] = 0, M[b1] =
1. Это говорит об отсутствии систематической ошибки при
определении положения линии регрессии.
2. Оценки состоятельны, т.к. при n D[b0] 0, D[b1]
0. Это означает, что с ростом n надежность оценок
возрастает.
3. Оценки эффективны, т.е. они имеют наименьшую
дисперсию по сравнению с любыми другими оценками
данных параметров, линейными относительно величин yi.
15
16. Типичная картина выполнения условий Гаусса – Маркова
1617. Типичная картина нарушения условий 20 и 40: D[] = const, Cov(i,Xi) = 0
Типичная картина нарушения условий20 и 40: D[ ] = const, Cov( i,Xi) = 0
17
18. Типичная картина нарушения условия 30: Cov(i,j) = 0, i j
Типичная картина нарушенияусловия 30: Cov( i, j) = 0, i j
18
19. Система показателей качества парной регрессии
1. Показатели качества коэффициентоврегрессии
2. Показатели качества уравнения
регрессии в целом
3. Адекватность модели – остатки должны
удовлетворять условиям теоремы ГауссаМаркова
19
20. Показатели качества коэффициентов регрессии
1. Стандартные ошибки оценок (анализ точностиопределения оценок).
2. Значения t-статистик (проверка гипотез
относительно коэффициентов регрессии).
3. Интервальные оценки коэффициентов
линейного уравнения регрессии.
4. Доверительные области для зависимой
переменной.
20
21. Стандартные ошибки оценок
Оценки b0 и b1 являются случайными величинами. Отсюдаследует, что стандартные ошибки коэффициентов
регрессии – это средние квадратические отклонения
коэффициентов регрессии от их истинных значений.
Можно показать, что дисперсии оценок b0 и b1 равны:
D[b1 ]
( x x)
i
x
2
2
2
, D[b0 ]
2
i
n ( xi x )
2
21
22. Свойства дисперсий оценок
1. Дисперсии D[b0] и D[b1] прямо пропорциональныдисперсии случайного отклонения 2. Следовательно, чем
больше фактор случайности, тем менее точными будут
оценки.
2. Чем больше число наблюдений n, тем меньше дисперсии
оценок.
3. Чем больше дисперсия объясняющей переменной, тем
меньше дисперсия оценок коэффициентов регрессии.
Другими словами, чем шире область изменений
объясняющей переменной, тем точнее будут оценки (тем
меньше доля случайности в их определении).
22
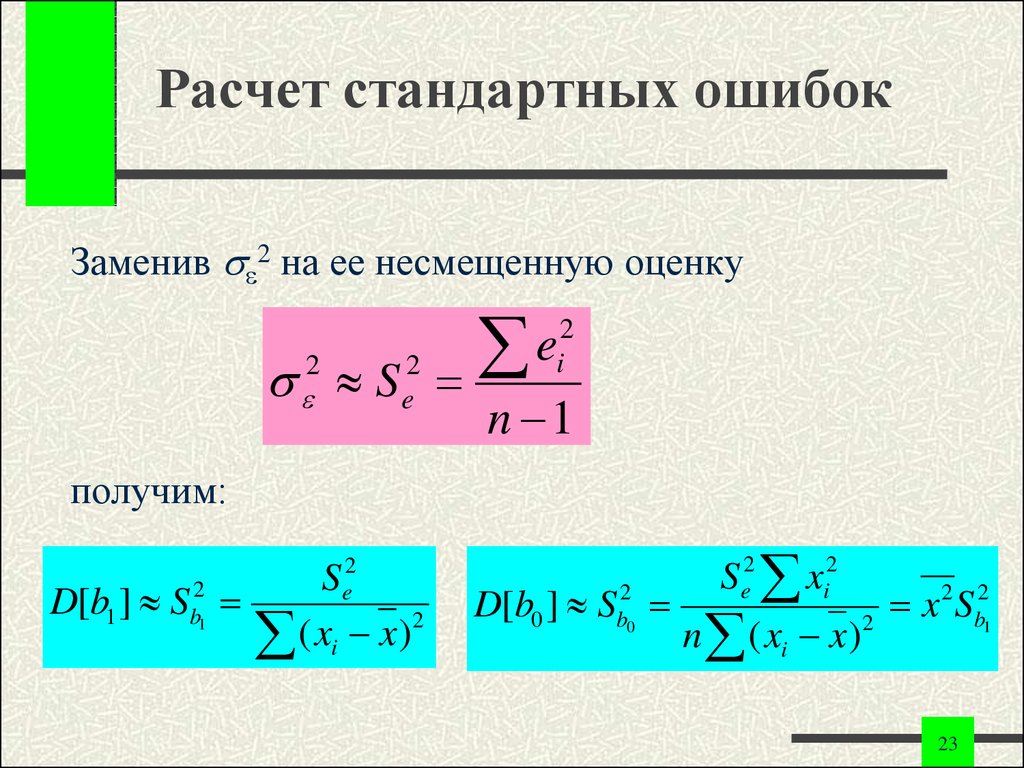
23. Расчет стандартных ошибок
Заменив 2 на ее несмещенную оценкуS
2
2
e
e
2
i
n 1
получим:
2
S
e
D[b1 ] Sb21
2
(
x
x
)
i
D[b0 ] Sb20
Se2 xi2
n ( xi x )2
x 2 Sb21
23
24. Формулы расчета стандартных ошибок оценок
Стандартные ошибки коэффициентов регрессии:Sb0 S
2
b0
Sb1 S
2
b1
Стандартная ошибка является оценкой среднего
квадратического отклонения коэффициента
регрессии от его истинного значения
24
25. Использование стандартных ошибок
Сравнивая значение коэффициента с егостандартной ошибкой, можно судить о
значимости коэффициента
Коэффициент называется значимым, если есть
достаточно высокая вероятность того, что его
истинное значение отлично от нуля
Для стандартных ошибок оценок нет таблиц критических
уровней – для точного суждения используются t-статистики
25
26. Проверка значимости на основе t-статистик
Проверка значимости на основе t-статистикзаключается в установлении наличия линейной
зависимости между Y и X. Данный анализ
осуществляется по схеме проверки статистических
гипотез. Проверяются альтернативные гипотезы:
H 0 : 1 0
и
H1 : 1 0
26
27. Проверка значимости на основе t-статистик
Если принимается гипотеза H0, то считают, что величина Y независит от X. В этом случае говорят, что коэффициент b1
статистически незначим (т.к. слишком близок к нулю). В
противном случае говорят, что коэффициент b1
статистически значим, что указывает на наличие линейной
зависимости между Y и X.
Для парной линейной регрессии более важным является анализ
статистической значимости коэффициента b1, т.к. именно в нем
скрыто влияние объясняющей переменной X на зависимую
переменную Y.
27
28. Значимость свободного члена
Аналогично проверяется значимость коэффициента b0.Однако мы должны быть осторожны в сильном
выделении свободного члена. Почему?
1. Мы обычно не имеем наблюдений вблизи X=0.
2. При отсутствии наблюдений на каком-либо участке
оцененная зависимость не может быть данном месте
достоверной.
28
29. t-статистики для проверки значимости коэффициентов регрессии
t-статистика соизмеряет значение коэффициентас его стандартной ошибкой:
b0
t (b0 )
Sb0
b1
t (b1 )
Sb1
29
30. t-статистики для проверки значимости коэффициентов регрессии
t-статистики в парной регрессии по n наблюдениямпри справедливости гипотезы H0 имеют
распределение Стьюдента с числом степеней
свободы l = n – 2
30
31. Порядок работы при проверке значимости коэффициента по t-статистике
1. Выбираем уровень значимости (1% или 5%).2. Вычисляем число степеней свободы (n 2).
3. По таблицам распределения Стьюдента определяем
критическое значение t /2; n-2 (двухсторонний критерий) или
t ; n-2 (односторонний критерий).
4. Если модуль t-статистики больше критического значения,
то коэффициент является значимым на уровне значимости
.
5. В противном случае коэффициент не значим (на данном
уровне ).
31
32. Использование односторонних гипотез для проверки значимости коэффициентов
Использование односторонних гипотез иногда позволяет«спасти» значимость коэффициентов регрессии при том
же уровне значимости
Это требует обязательного экономического обоснования
32
33. Пример (A). Проверка значимости
2e
i
2
e
S
35,249
S
0,001490
2
2
( xi x) (n 2) ( xi x) 10 2366,3
2
b1
b1 0,9361
Sb1 0,00149 0,03860 tb1
24,25
Sb1 0,0386
Критическое значение при уровне значимости = 0,05:
têð t
2
; n 2
t0,025;10 2,634
33
34. Пример (A). Проверка значимости
tb1 24,25 2,634 têðПоэтому нулевая гипотеза H0: { 1 = 0} отвергается в пользу
альтернативной при выбранном уровне значимости.
Следовательно, коэффициент регрессии b1 статистически
значим
Аналогично проверяем статистическую значимость
коэффициента b0
34
35. Пример (A). Проверка значимости
Sb20 x 2 Sb21 0,00149 15884,75 23,663Sb0 23,663 4,864
b0 3,423
tb0
0,704
Sb0 4,864
tb0 0,704 2,634 têð
Гипотеза о статистической незначимости b0 не отклоняется.
Это означает, что свободным членом уравнения регрессии
можно пренебречь, рассматривая регрессию как Y = b1X
35
36. Правило оценки значимости коэффициентов регрессии без использования таблиц
1. Если tb 1 , то коэффициент bi не м.б. признанзначимым, т.к. доверительная вероятность менее 0,7.
2. Если 1 tb 2 , то найденная оценка может
рассматриваться как относительно (слабо) значимая. При
этом доверительная вероятность лежит между 0,7 и 0,95.
3. Если 2 tb 3 , то коэффициент значим. Доверительная
вероятность лежит между значениями 0,95 и 0,99.
4. Если tb 3 , то это почти полная гарантия значимости
коэффициента.
i
i
i
i
36
37. Интервальные оценки коэффициентов линейного уравнения регрессии
Построение доверительных интервалов для коэффициентовлинейной регрессии при заданном уровне значимости :
для 0:
для 1:
b0 t Sb0 ; b0 t Sb0
,n 2
,n 2
2
2
b1 t Sb1 ; b1 t Sb1
,n 2
,n 2
2
2
Доверительные интервалы с надежностью (1 )
накрывают истинные значения 0 и 1
37
38. Порядок работы при проверке значимости коэффициента по доверительному интервалу
1. Выбираем уровень значимости (1% или 5%).2. Вычисляем число степеней свободы (n 2).
3. По таблицам распределения Стьюдента определяем
критическое значение t /2; n-2 (двухсторонний критерий).
4. Вычисляем границы доверительного интервала.
5. Если точка 0 (ноль) не лежит внутри доверительного
интервала, то коэффициент является значимым на уровне
значимости .
6. В противном случае коэффициент не значим (на данном
уровне ).
38
39. Доверительные области для зависимой переменной
Одной из центральных задач эконометрики являетсяпрогнозирование значений зависимой переменной при
определенных значениях объясняющих переменных.
Здесь возможны два варианта:
1. Предсказать условное математическое ожидание
зависимой переменной при определенных значениях
объясняющих переменных (предсказание среднего
значения).
2. Предсказать некоторое конкретное значение зависимой
переменной (предсказание конкретного значения).
39
40. Предсказание среднего значения зависимой переменной
Пусть построено уравнение регрессииy( xi ) b0 b1 xi
На его основе необходимо предсказать условное м. о.
M [Y / X x p ] 0 1 x p
переменной Y при X = xp.
Вопрос: Как сильно может уклониться значение y ( x p ) от
M [Y / X x p ]
40
41. Предсказание среднего значения зависимой переменной
Доверительная область для условного м. о. M[Y/X = xp]:b0 b1 x p t S y ( x ) ; b0 b1 x p t S y ( x )
p
p
,n 2
,n 2
2
2
S y2( x p )
2
(
x
x
)
1
p
2
Se
2
n ( x x)
i
При x p x она минимальна, а по мере удаления xp от x
величина доверительной области увеличивается
41
42. Предсказание индивидуальных значений зависимой переменной
Построенная доверительная область для Mx[Y] определяетместоположение модельной линии регрессии (условного м.о.),
а не отдельных возможных значений зависимой переменной,
которые отклоняются от среднего x .
Оценка дисперсии индивидуальных значений y p b0 b1 x p
при x = xp равна
2
S
yp
2
( x p x)
1
2
Se 1
n ( x x )2
i
42
43. Предсказание индивидуальных значений зависимой переменной
Доверительная область для прогнозов индивидуальныхзначений y p имеет вид:
b0 b1 x p t
2
,n 2
S y p b0 b1 x p t
yp
2
,n 2
S
yp
Доверительная область для индивидуальных
значений y p шире доверительной области для
условного м.о. M [Y / X x p ]
43
44. Графики доверительных областей для зависимой переменной
4445. Выводы по доверительным областям для зависимой переменной
1. Прогноз значений зависимой переменной Y поуравнению регрессии оправдан, если значение x
объясняющей переменной X не выходит за диапазон
ее значений по выборке. Причем, чем ближе xp к x,
тем точнее прогноз (уже доверительный интервал).
2. Использование линии регрессии вне обследованного
диапазона значений объясняющей переменной (даже
если оно оправдано, исходя из смысла решаемой
задачи) может привести к значительным
погрешностям.
45
46. Пример (А). Доверительные области для зависимой переменной
1. Рассчитаем 95%-й доверительный интервал дляусловного м.о. при xp = 160. Границы интервала
равны:
1 (160 125,25)2
3,423 0,9361 160 2,634 1,8775
12
2366,25
Отсюда среднее потребление при доходе 160 д.е. с
вероятностью 95% будет находиться в интервале:
(149,39; 157,01)
46
47. Пример (А). Доверительные области для зависимой переменной
2. Границы 95%-го доверительного интервала дляиндивидуальных объемов потребления равны:
1 (160 125,25)2
3,423 0,9361 160 2,634 1,8775 1
12
2366,25
Отсюда интервал, в котором будут находиться, по
крайней мере 95% индивидуальных объемов
потребления при доходе xp = 160, равен:
(146,96; 159,44)
47
48. Показатели качества уравнения регрессии в целом
Суть проверки общего качества уравнения регрессии –оценить насколько хорошо эмпирическое уравнение
регрессии согласуется со статистическими данными.
Основные показатели качества:
1. Коэффициент детерминации R2.
2. Значение F-статистики.
3. Коэффициент корреляции rxy.
4. Сумма квадратов остатков (RSS).
5. Стандартная ошибка регрессии Se.
6. Средняя ошибка аппроксимации.
48
49. Коэффициент детерминации R2
Коэффициент R2 показывает долю объясненнойвариации зависимой переменной:
R 1
2
2
e
i
( y
i
y)
2
Используется для предварительной оценки качества
модели и как основа для расчета других показателей
Коэффициенты R2 в разных моделях с разным
числом наблюдений (и переменных) несравнимы
49
50. Основные свойства коэффициента детерминации
1.2.
3.
4.
0 R2 1.
Чем ближе R2 к 1, тем лучше регрессия аппроксимирует
статистические данные, тем теснее линейная связь
между зависимой и объясняющими переменными.
Если R2 = 1, то статистические данные лежат на линии
регрессии, т.е. между зависимой и объясняющими
переменными имеется функциональная зависимость.
Если R2 = 0, то вариация зависимой переменной
полностью обусловлена воздействием неучтенных в
модели переменных.
В случае парной регрессии R2 = rxy2.
50
51. Пример (А). Расчет коэффициента детерминации
e2
i
35,249
R 1
1
0,983
2
2108,667
( yi y )
2
51
52. F-тест на качество оценивания уравнения регрессии
Основан на основном тождестве дисперсионного анализаn
Var( y ) Var( y ) Var(e)
( y y) ( y y) e
2
2
i
i
TSS
ESS
2
i
RSS
TSS – общая сумма квадратов отклонений
ESS – объясненная сумма квадратов отклонений
RSS – необъясненная сумма квадратов отклонений
52
53. F-статистика для проверки качества уравнения регрессии
F-статистика представляет собой отношение объясненнойсуммы квадратов (в расчете на одну независимую
переменную) к остаточной сумме квадратов (в расчете на
одну степень свободы)
F Fфакт
2
(
y
y
)
i
m
2
(
y
y
)
i i
n m 1
ESS
m
,
RSS
n m 1
n – число выборочных наблюдений, m – число
объясняющих переменных
53
54. F-статистика для проверки качества уравнения регрессии
При отсутствии линейной зависимости между зависимойи объясняющими(ей) переменными F-статистика имеет Fраспределение Фишера-Снедекора со степенями свободы
k1 = m, k2 = n – m –1.
Уравнение регрессии значимо на уровне , если
Fфакт F ;k1 ;k2 ,
где F ;k1 ;k 2 – табличное значение F-распределения,
определенное на уровне значимости при степенях
свободы k1 и k2
54
55. F-статистика для проверки качества парного уравнения регрессии
В парной (m = 1) регрессии F-статистика являетсяотношением объясненной суммы квадратов к остаточной
сумме квадратов (в расчете на одну степень свободы),
причем m = 1, n – m –1 = n – 2.
ESS / m
( ESS / TSS ) / m
R2
F
RSS /( n m 1) ( RSS / TSS ) /( n m 1) (1 R2 ) /( n 2)
F-статистика в парной регрессии по n наблюдениям
имеет F-распределение с 1 и (n–2) степенями свободы
55
56. Порядок работы при проверке значимости парного уравнения по F-статистике
1. Выбираем уровень значимости (1% или 5%).2. Вычисляем число степеней свободы 1 и (n 2).
3. По таблицам F-распределения определяем
критическое значение F ; 1; n-2 (всегда одностороннее).
4. Если F-статистика больше F ; 1; n-2 , то уравнение в целом
является значимым на уровне значимости .
5. В противном случае уравнение в целом не значимо (на
данном уровне ).
56
57. Связь между значимостью коэффициента регрессии и уравнения в целом
В парной регрессии F-статистика равна квадратуt-статистики; то же верно и для их критических
уровней (односторонний для t-статистики)
t F
2
t
; n 2
2
F ;1; n 2
В парной регрессии значимость коэффициента регрессии
и значимость уравнения в целом эквивалентны
F-статистики в разных моделях с разным числом
наблюдений и (или) переменных несравнимы
57
58. Коэффициент корреляции rxy
Коэффициент корреляции указывает на наличие(или отсутствие) линейной связи между зависимой
и объясняющей переменными
Для проверки гипотезы об отсутствии линейной связи
используется тот факт, что величина
n 2
t r
2
1 r
имеет распределение Стьюдента с (n–2) степенями свободы
58
59. Взаимосвязь критериев в парном регрессионном анализе
Коэффициент корреляции по абсолютной величинесовпадает с квадратным корнем из коэффициента
детерминации
rxy R
2
t-статистики для коэффициента корреляции и
коэффициента регрессии b1 совпадают
Проверка значимости коэффициента регрессии
эквивалентна проверке наличия линейной связи
59
60. Проверка значимости коэффициента детерминации
Критическое значение R2 связано скритическим значением F-статистики
2
крит
R
mFкрит
mFкрит (n m 1)
mF ; m; n m 1
mF ; m; n m 1 (n m 1)
,
Проверка значимости коэффициента
детерминации эквивалентна проверке
значимости уравнения регрессии в целом
60
61. Сумма квадратов остатков RSS
Является оценкой необъясненной частивариации зависимой переменной
n
RSS e
i 1
2
i
Используется как основная минимизируемая величина в
МНК, а также для расчета других показателей
Значения RSS в разных моделях с разным числом
наблюдений и (или) переменных несравнимы
61
62. Стандартная ошибка регрессии Se
Является оценкой величины квадрата ошибки,приходящейся на одну степень свободы модели
n
Se
2
e
i
i 1
n m 1
Используется как основная величина для измерения
качества модели (чем она меньше, тем лучше)
Значения Se в однотипных моделях с разным числом
наблюдений и (или) переменных сравнимы
62
63. Средняя ошибка аппроксимации A
Оценку качества модели дает также средняя ошибкааппроксимации
– среднее отклонение расчетных значений
y i зависимой переменной от фактических значений yi
1 n yi y i
A
100%.
n i 1 yi
Допустимый предел значений A – не более 10%.
Чем меньше значение A, тем лучше
Значения A в моделях с разным числом наблюдений
и одинаковым количеством переменных сравнимы
63
64. Типичные ошибки в использовании показателей качества регрессии
Величина коэффициентов регрессии не указывает на силусвязи или силу влияния на зависимую переменную
Значимость коэффициентов по t-тестам не позволяет
сделать вывод о справедливости тех или иных теорий
t-статистики не указывают на относительную важность
коэффициентов регрессии
t-статистики предназначены для использования
исключительно для выборки и бесполезны для анализа
всей совокупности
Нельзя сравнивать t-статистики, F-статистики,
коэффициенты детерминации и др. у разных уравнений
64
65. Ограниченность простой регрессии
1. Никакая единственная переменная за редкимиисключениями не в состоянии хорошо «объяснить»
изменения зависимой переменной.
2. Могут существовать несколько одинаково хороших и
взаимно противоречивых регрессий.
3. Наконец, линейная форма примитивна.
И тем не менее: Нет ничего лучше по простоте и
ясности объяснения парной линейной связи. При
равной объясняющей способности из двух моделей мы
всегда выбираем более простую.
65
66.
Конец лекции66
















![Типичная картина нарушения условий 20 и 40: D[] = const, Cov(i,Xi) = 0 Типичная картина нарушения условий 20 и 40: D[] = const, Cov(i,Xi) = 0](https://cf.ppt-online.org/files/slide/r/rCwm7heAj6lXbcZygfViSTWBxDQd4s1oIa35pR/slide-16.jpg)
















































 mathematics
mathematics








