Спецификация переменных в уравнениях регрессии

1. Спецификация переменных в уравнениях регрессии

1. Ошибки спецификации.
2. Влияние неполноты включения
уравнения переменных.
3. Влияние избыточности факторов.
4. Лаговые переменные.
в

2. Моделирование

• Вопросы:
К каким результатам приведет включение в уравнение регрессии
переменной, которой там недолжно быть;
Каковы последствия отсутствия переменной, которая должна
присутствовать;
Что произойдет, если вместо некоторых исходных данных решим
использовать «заменители».

3. Результаты неправильной спецификации переменных

Опущена необходимая переменная –
Оценки коэффициентов регрессии оказываются
смещенными,
Стандартные ошибки коэффициентов и t-тесты в целом
становятся некорректными
Включена ненужная переменная –
Оценки коэффициентов регрессии оказываются
несмещенными, однако неэффективными;
Стандартные ошибки в целом корректны, но из-за
эффективности будут излишне большими.

4. Влияние отсутствия необходимой переменной

Проблема смещения
истинная модель
y= x1 + x2
строим модель y= x1
cov( x1 , y )
cov( x1 , x2 )
E
1 2
var(x1 )
var( x1 )
Неприменимость статистических тестов

5. Свойства коэффициентов регрессии

• Интерпретация коэффициентов регрессии
• Несмещенность коэффициентов
• Точность коэффициентов
• Предположения:
1) выполняются 4 условия Гаусса-Маркова
2) имеется достаточное количество данных
3) между независимыми переменными нет строгой линейной
зависимости

6. Интерпретация коэффициентов регрессии

• Утверждение
bi – оценивает влияние xi на y при неизменности влияния на y
остальных переменных
• Для p=2 оценка коэффициента b1 по МНК
Cov( x1 , y )Var ( x2 ) Cov( x2 , y )Cov( x1 , x2 )
b1
2
Var ( x1 )Var ( x2 ) Cov( x1 , x2 )
• Доказательство утверждения: см. на доску

7. Несмещенность

• Случай p=2
• Теорема
1
b1 1 Cov( x1 , u )Var ( x2 ) Cov( x2 , u )Cov( x1 , x2 )
Var ( x1 )Var ( x2 ) Cov( x1 , x2 )
• где
• Следствие
2
E (b1 ) 1
• доказательство
1
E (b1 ) 1 Var ( x2 ) E Cov( x1 , u ) Cov( x1 , x2 ) E Cov( x2 , u ) 1

8. Точность

• МНК дает наиболее эффективные линейные оценки
(теорема Гаусса-Маркова)
• Факторы, влияющие на точность:
ЧИСЛО НАБЛЮДЕНИЙ В ВЫБОРКЕ;
ДИСПЕРСИЯ ВЫБОРКИ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ;
ТЕОРЕТИЧЕСКАЯ ДИСПЕРСИЯ СЛУЧАЙНОГО ЧЛЕНА;
СВЯЗЬ МЕЖДУ СОБОЙ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ.
• Доказательство для случая p=2
1
Var (bi )
2
nVar ( xi ) 1 rx1x2
2
u

9. Стандартные ошибки коэффициентов регрессии

• «Стандартная
ошибка» коэффициента множественной
регрессии - оценка стандартного отклонения распределения
коэффициента регрессии
Для случая p=2:
mbi
1
2
nVar ( xi ) 1 rx1x2
2
u
n /( n 3)Var (e)
1
nVar ( xi )
1 rx21x2
Var (e)
1
2
(n 3)Var ( xi ) 1 rx1x2

10. Мультиколлинеарность

• Мультиколлинеарность – понятие, используемое для
описания ситуации, когда нестрогая линейная зависимость
приводит к получению ненадежных оценок регрессии
• Замечание 1: если другие факторы благоприятны, то можно
получить и хорошие оценки
• Замечание 2: проблема мультиколлинеарности является
обычной для временных рядов

11. Проверка мультиколлинеарности факторов

Проверяем гипотезу о независимости переменных
H0: det R=1
Теорема
Величина
1
n
1
(
2
m
5
)
lg
det
R
6
асимптотически имеет
2
-распределение с 0,5n(n-1) степенями
свободы.
Следствие
2
если факт
2
табл ( df , ) , то гипотеза H0 отклоняется

12. Методы смягчения мультиколлинеарности

• А) Попытки повысить степень выполнения четырех
параметров:
• число наблюдений;
• выборочные дисперсии объясняющих переменных;
• дисперсия случайного члена.
• Б) использование внешней информации:
• теоретические ограничения;
• внешние эмпирические оценки.

13. F-тест

• F-статистика
F
Dфакт
Dост
2
yi y / k
2
y y x /(n k 1)
2
R
k
2
1 R n k 1
• F–тест оценивает значимость уравнения в целом:
1 2 ... k 0
• проверяется гипотеза H :
0

14. Качество оценивания: коэффициент R2

• R2 – один из ряда диагностических показателей
(причем не самый важный)
• Скорректированный R2
n 1
k
2
R 1 (1 R )
R
(1 R 2 )
n k 1
n k 1
2
2

15. Дальнейший анализ дисперсии

ESS – объясненная сумма квадратов
RSS – остаточная сумма квадратов
2 этапа оценивания:
оцениванием регрессию с k независимыми переменными
оцениванием регрессию с m>k независимыми переменными
Гипотеза H0: дополнительные переменные не увеличивают объяснение
регрессией
F-статистика:
( RSS k RSS m ) /( m k )
F
RSS m /( n m 1)

16. Зависимость между F- и t-статистиками

• t-тест обеспечивает проверку предельного вклада каждой
переменной при допущении, что все другие переменные
уже включены в уравнение
• t-тест эквивалентен F-тесту для предельного вклада
переменной, которая была отброшена
• Замечание: возможна ситуация, когда t-тест для каждой
переменной незначим, а F-тест для уравнения в целом
значим.
Объяснение: если объясняющие способности независимых
переменных перекрываются, т.е. имеется мультиколлинеарность.

17. Поведение R2 при невключении объясняющей переменной

• Значение R2 может быть смещено вверх (при
положительной корреляции объясняющих
переменных) или вниз ( при отрицательной
корреляции)

18. Замещающие переменные

• Вместо отсутствующей переменной используем
заменитель (proxy)
• Пример.
ln
y
ln
x
ln
p
u
1
2
• модель
• y – расходы потребителя на питание
• x – располагаемый личный доход
• p – относительная цена продовольствия
• Пусть lnx имеет явно выраженный временной
тренд, тогда время t можно использовать как
заменитель x
ln y a b2 ln p b3t

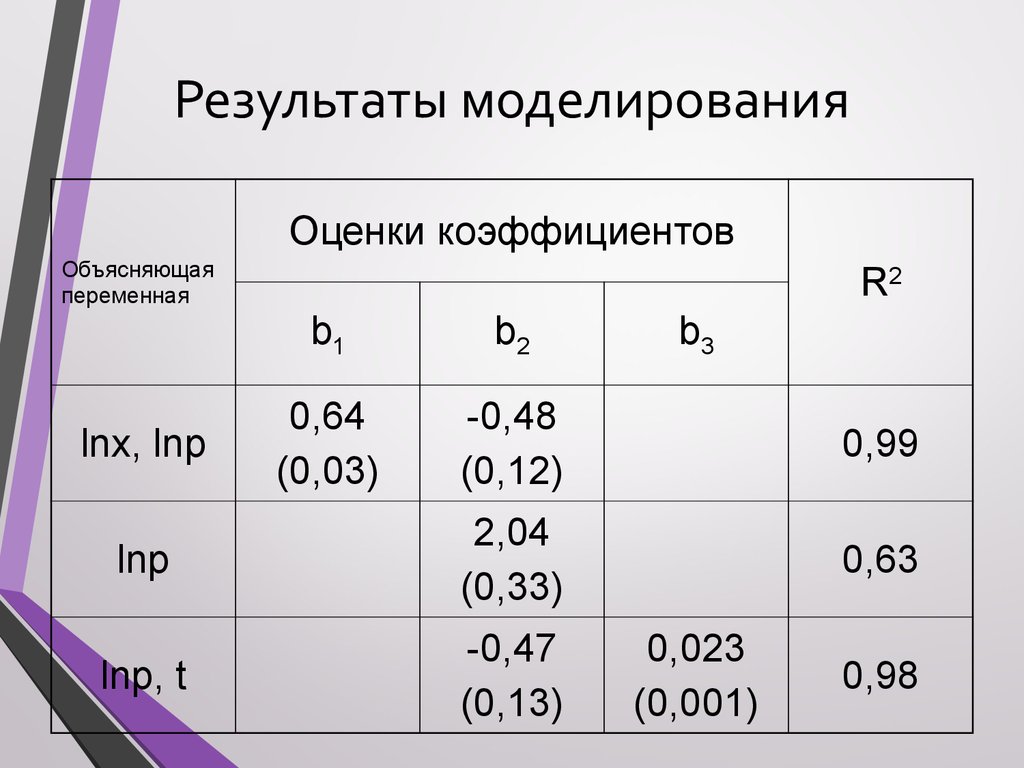
19. Результаты моделирования

Оценки коэффициентов
Объясняющая
переменная
R2
b1
b2
0,64
(0,03)
-0,48
(0,12)
0,99
lnp
2,04
(0,33)
0,63
lnp, t
-0,47
(0,13)
lnx, lnp
b3
0,023
(0,001)
0,98

20. Непреднамеренное использование замещающих переменных

• Если корреляция между z и x незначительна, то результаты будут плохими
• Если корреляция между z и x тесная, то результаты будут удовлетворительными
• Если цель регрессии – предсказание значений y, то использование замещающих
переменных целесообразно
• Если
цель регрессии – научное любопытство, то использование замещающих
переменных обычно нецелесообразно
• Если хотим использовать объясняющую переменную как инструмент экономической
политики, то последствия использования замещающей переменной могут быть
катастрофическими

21. Анализ остатков

• Взгляд пессимиста:
• свидетельство неудачи
• Взгляд оптимиста:
• источник новых идей
• основа для постановки новых задач
• конструктивная критика
• Пример: продажа предметов длительного пользования

22. ЛАГОВЫЕ ПЕРЕМЕННЫЕ

• лаговые переменные – это экзогенные или
эндогенные переменные, которые относятся к
предыдущим моментам времени и находятся
в эконометрической модели одновременно с
переменными, относящимися к текущему
моменту времени.
• Например,
xt-1 – это лаговая экзогенная
переменная, а yt-1 – это лаговая эндогенная
переменная