Similar presentations:
Множественная регрессия
1. 4. Множественная регрессия
2. 1
Парная регрессия может дать хорошийрезультат, если удается выделить один главный
фактор, а влиянием остальных факторов можно
пренебречь. Очевидно, что не всегда это удается
сделать. В качестве примера рассмотрим
следующую задачу.
1
Для объяснения изменения ВНП (Y) за 10 лет
требуется построить регрессионную модель с
объясняющими переменными - х1 (объем
потребления) и х2 (объем инвестиций).
Статистические данные приведены на следующем
слайде.
3. 2
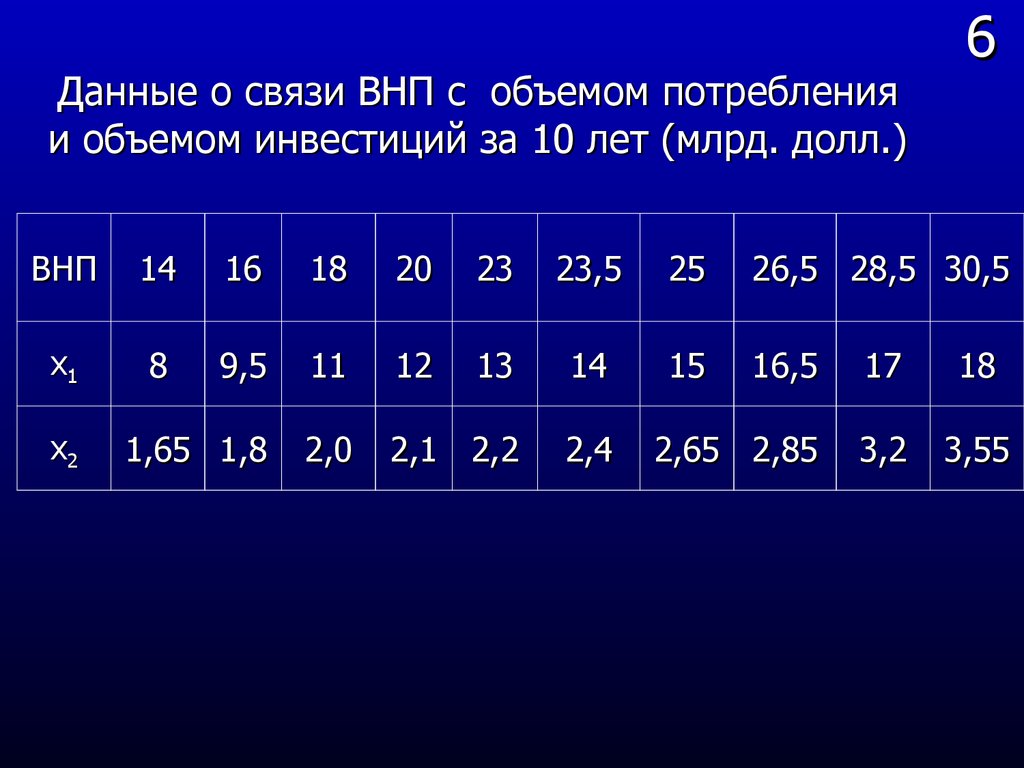
Данные о связи ВНП с объемом потребленияи объемом инвестиций за 10 лет (млрд. долл.)
ВНП
14
16
18
20
23
23,5
25
26,5 28,5 30,5
х1
8
9,5
11
12
13
14
15
16,5
17
18
1,65 1,8
2,0
2,1 2,2
2,4
2,65 2,85
3,2
3,55
х2
Найдем коэффициенты корреляции между
ВНП и объемом потребления ryx1 и между ВНП и
объемом инвестиций ryx2.
ryx1 0,99;
ryx2 0,96.
4. 3
Поскольку оба коэффициента корреляцииоказались весьма большими нельзя пренебречь
влиянием какого либо одного фактора и придется
строить уравнение множественной регрессии,
когда предполагается, что результирующий
признак y зависит от объясняющих переменных x1
и x2. В общем случае модель множественной
линейной регрессии будет выглядеть так
y a b1 x1 b 2 x 2 ...
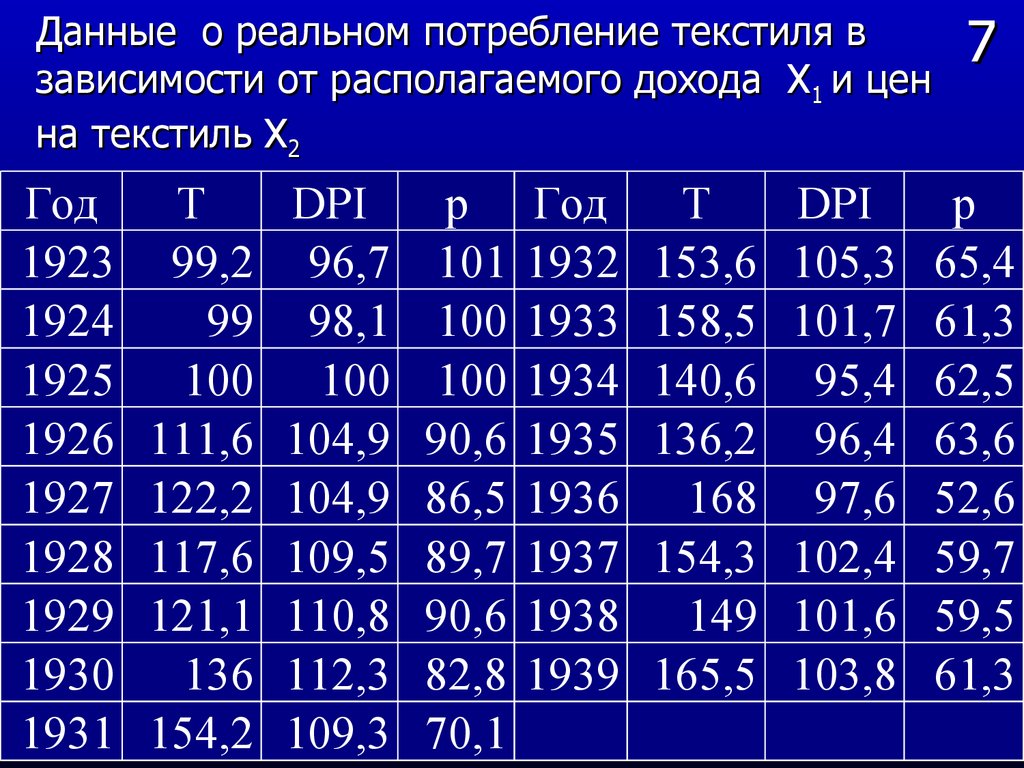
b n x n .
5. 4
Естественно, что множественная регрессияможет быть и нелинейной. Примером может
служить известная производственная функция
Кобба-Дугласа, определяющая зависимость
объема выпуска продукции Y от капитальных
затрат K и затрат труда L
1
Y A K L
Здесь А- некоторая константа,
показатель степени
1 0.
.
4
6. 4.1. Спецификация модели множественной регрессии
7. 1
Под спецификацией модели понимается выборосновных параметров модели таких как вид
математической функции реализующих модель,
отбор объясняющих переменных и проверка
основных положений регрессионного анализа для
эмпирических данных, на основании которых
строится модель.
Ограничимся вначале случаем множественной
линейной регрессии.
Поскольку самым распространенным методом
нахождения параметров множественной линейной
регрессионной модели остается метод МНК напомним
еще раз предпосылки его применения.
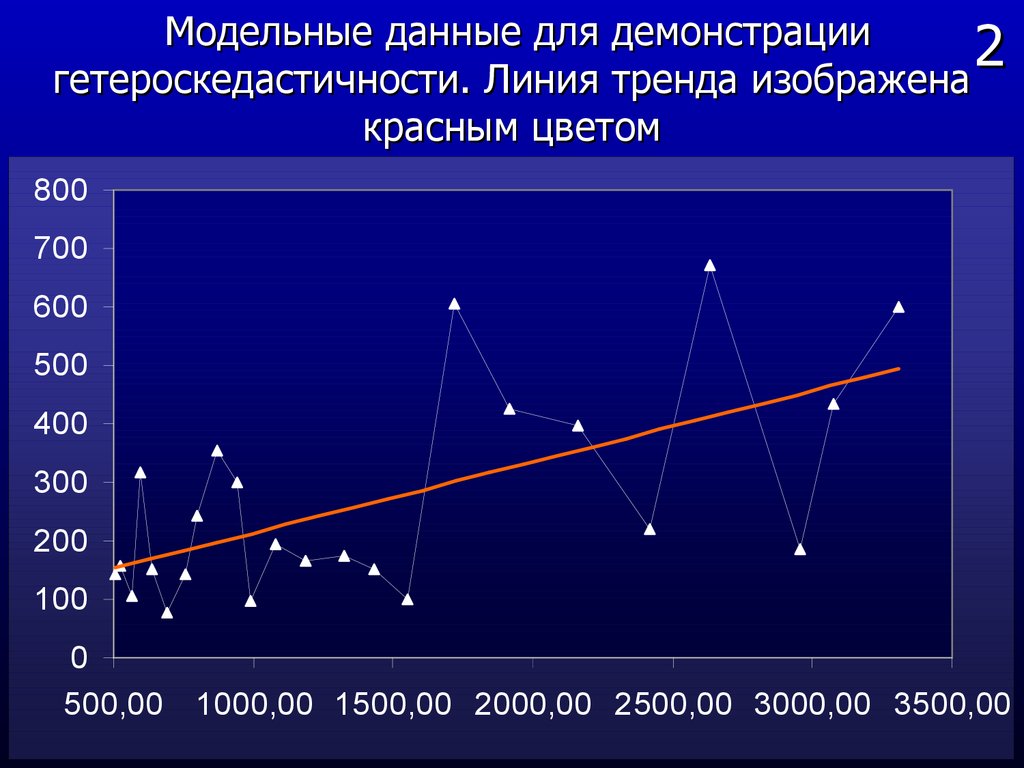
8. 2
Так же как и в случае однофакторной регрессии2должны выполняться постулаты 1-5.
1. В рассматриваемой регрессионной модели
случайными величинами являются yi и i , а xi
случайной величиной не является.
2. Математическое ожидание
M( εi ) 0.
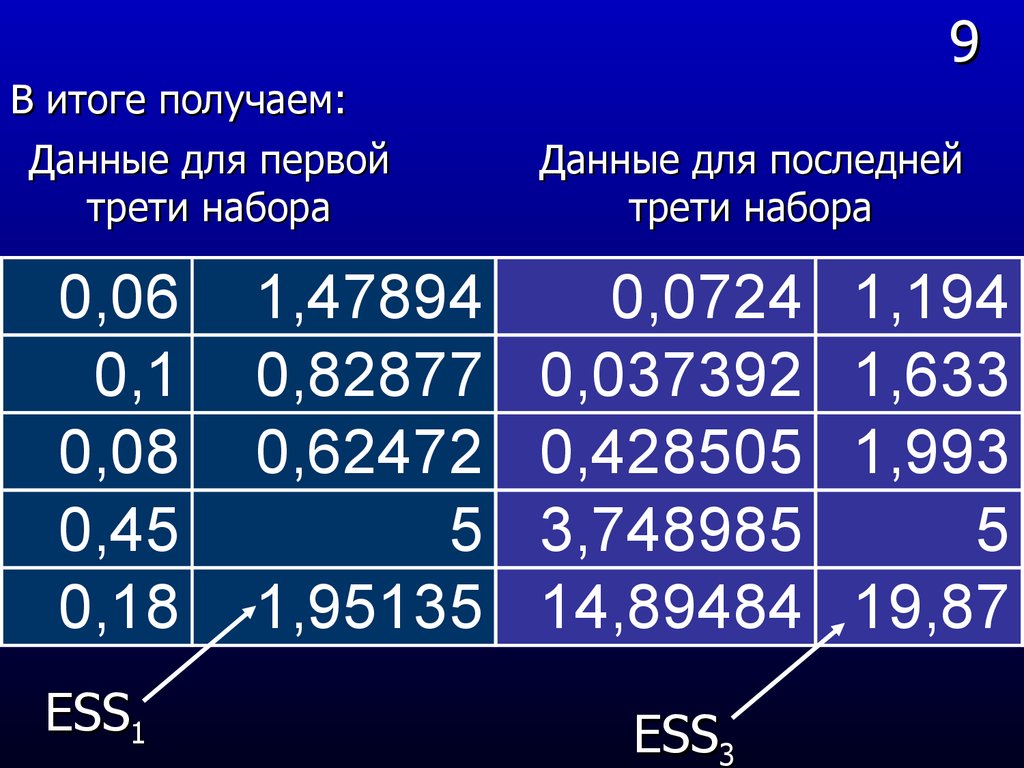
3. Дисперсия возмущения εi или зависимой
переменной yi постоянна и не зависит от номера
точки i (условие гомоскедастичности или
равноизменчивости возмущения)
D( εi ) 2 .
9. 3
4. Возмущенияεi и j
являются
3
независимыми. Отсюда следует, что
M ( εi j ) 0.
5. Возмущение
εi
или зависимая переменная уi
распределены по нормальному закону. Последнее
условие позволяет произвести оценку статистической
значимости модели и коэффициентов регрессии.
6. Отсутствие мультиколлинеарности. Между
объясняющими переменными должна отсутствовать
сильная линейная зависимость.
10. 4
По сравнению с однофакторной регрессией4
новым является шестой пункт, который требует
проверки включаемых в регрессионную модель
переменных на мультиколлинеарность (отсутствие
взаимной связи). Взаимосвязь переменных
встречается весьма часто. В частности, в
рассмотренном выше примере коэффициент
корреляции весьма высок
rx1x2 0,968.
По этой причине нельзя считать, что факторы х1 и
х2 являются независимыми. Включение в уравнение
связанных между собой переменных приводит к
тому, что коэффициенты регрессионного уравнения
оказываются не интерпретируемыми.
11. 5
Не существует метода, который бы сразууказывал, какие из переменных следует включить в
модель, а какие нет. По этой причине следует
пользоваться одной из возможных стратегий,
например, стратегией последовательного
включения.
1. Вычислить коэффициенты корреляции между
зависимой переменной и каждой из объясняющих
переменных. Выделить фактор с наибольшим
коэффициентом корреляции.
2. Построить уравнение регрессии, учитывая пока
только этот один объясняющий фактор. Найти
величину коэффициента детерминации R2 .
12. 6
3. Добавить в регрессионную модель следующий6фактор, имеющий наибольшую корреляционную
связь с зависимой переменной. Построить
двухфакторную регрессионную модель и найти
новое значение коэффициента детерминации. Если
коэффициент детерминации увеличился
незначительно, то добавление фактора не
улучшает модель, а только затрудняет ее
интерпретацию.
Таким образом, хотя есть возможность учесть
любое число факторов, в этом нет необходимости.
Включение лишних факторов приводит к
статистической не значимости параметров
регрессионного уравнения.
13. 7
Для иллюстрации сказанного вновь обратимсяк примеру, который мы уже рассматривали о
связи ВНП с объемом потребления и
инвестициями. Оба коэффициента корреляции
весьма велики.
ryx1 0,99;
ryx2 0,96.
Данные о связи ВНП с объемом потребления и
объемом инвестиций за 10 лет (млрд. долл.).
ВНП
14
16
18
20
23
23,5
25
26,5 28,5 30,5
х1
8
9,5
11
12
13
14
15
16,5
17
18
1,65 1,8
2,0
2,1 2,2
2,4
2,65 2,85
3,2
3,55
х2
14. 8
С помощью функции ЛИНЕЙН ( ) строимоднофакторную модель
8
y = 1,6254*x1 +0,7399
R2 = 0,9878
Добавим вторую переменную и построим
двухфакторную регрессионную модель, снова
используя функцию ЛИНЕЙН ( )
b2 = 0,902
b1 = 1,46
a = 0,696
mb2 = 1,422 mb1 = 0,265 ma = 0,913
R2 = 0,988
S = =0,660
F = 300,478 n-2 = 7
RSS = 261,45 ESS = 3,045
15. 9
Запишем уравнение двухфакторнойрегрессионной модели:
T
y 1,46 x1 0,902 x 2 0,696.
Как следует из приведенных результатов,
регрессионные коэффициенты двух рассмотренных
выше моделей различаются очень сильно, а
коэффициенты детерминации практически
неразличимы ( R=0,0007 различие в четвертом
знаке после запятой).
16. 10
Обращаем внимание на то, что экономическийсмысл коэффициента стал совершенно другим. Если
в случае однофакторной модели при увеличении
потребления на 1 млрд. руб. объем ВНП
увеличивается на 1,62 млрд. руб., то в случае
двухфакторной дисперсии увеличение потребления
на 1 млрд. руб. приводит к увеличению объема
ВНП на 1,4629 млрд. руб.
Очевидно, что добавление второй переменной
здесь является некорректным. Скорее всего
объясняющими переменными должна быть какая-то
линейная комбинация переменных х1 и х2.
17. 11
Обычно считается, что переменные явноколлинеарны, т.е. находятся в линейной
зависимости между собой. если
коэффициент корреляции между ними если
11
rij 0,7.
Вычисление парных коэффициентов корреляции
позволяет обнаружить явную корреляцию
объясняющих переменных. Наибольшую
трудность вызывает наличие
мультиколлинеарных факторов, когда более чем
два фактора связаны между собой линейной
зависимостью.
18. 12
Для оценки мультиколлинеарности факторовобычно используют определитель матрицы парных
коэффициентов корреляции между факторами.
Пусть имеется регрессионное уравнение с тремя
объясняющими переменными
T
y b1 x1 b 2 x 2 b3 x 3 b 0 .
Составим определитель коэффициентов
корреляции
19. 13
1Det( r ) rx1x2
rx1x3
rx2 x1
1
rx2 x3
rx3 x1
rx3 x2
1
13
Если переменные не коррелированны, то
недиагональные компоненты равны нулю и
определитель равен единице. Если, наоборот, все
переменные коррелированны, то определитель
будет иметь два одинаковых столбца и тогда он
равен нулю.
20. 14
Оценка значимости мультиколлинеарностифакторов может быть проведена методом
испытания гипотезы об отсутствии
мультиколленеарности (Н0). Доказано, что
величина
2
факт
14
1
n 1 ( 2m 5 ) lg(Det(r))
6
имеет распределение хи-квадрат с
1
k n ( n 1 )
2
числом степеней свободы.
2
факт
2
крит
Если
То гипотеза Н0 отклоняется и
мультиколлинеарность считается доказанной.
21. 4.2 Выбор формы уравнения регрессии
22. 1
Как уже указывалось, наряду с линейнойформой регрессионного уравнения, может быть
использованы и нелинейные регрессионные
уравнения и в первую очередь уравнения
регрессии, которые могут быть приведены к
линейным с помощью замены переменных.
1
Приведем вид функций для некоторых моделей
1. Линейная форма
y a b1 x1 b 2 x 2 ...
b n x n .
23. 2
Примером линейной модели может быть модель 2Фридмана, который построил для США по данным
за 1905 - 1951 гг. следующую функцию
потребления
Ct 0,58 R t 0,32 R t -1 53.
Согласно этой модели потребление в момент
времени t зависит от дохода того же периода Rt и
дохода предшествующего периода. Коэффициент при
переменной Rt называют краткосрочной предельной
склонностью к потреблению, а сумму
коэффициентов при Rt и Rt-1 - долгосрочной
склонностью к потреблению.
24. 3
Обратим внимание на то, что свободный член влинейном уравнении регрессии очень часто не
имеет экономической интерпретации.
2. Степенная форма уравнения множественной
регрессии
y
b1
a x1
b2
x2
bn
... x n
;
Степенная форма уравнения регрессии
получила широкое распространение в связи с
построением производственных функций.
Примером может служить функция Кобба-Дугласа.
Y A K L .
3
25. 3а
Степенная форма сводится к линейной, есливвести новые переменные. Действительно,
прологарифмируем уравнение
3а
ln y ln a b1ln x1 b 2ln x 2
... b n ln x n ;
Поэтому для линеаризации достаточно ввести
новые переменные
ln y Z, ln x1 X 1 , ln x 2 X 2 ,
ln x n X n .
26. 4
Известен также закон Энгеля для расходов на4
питание в США в зависимости от доходов, который
имеет вид
Y 3,22 x
0,55
.
Экономический смысл параметров регрессионного
уравнения в случае степенной модели легко
понять. если вычислить частные эластичности по
переменным модели (K, L, например).
EY
K
EY
L
dY K
;
dK Y
dY L
.
dL Y
27. 5
Эластичность показывает на сколькопроцентов изменится функция при изменении
аргумента на один процент. В случае функции
Кобба -Дугласа параметры и
показывают, что объем производства
увеличится на процентов при увеличении
капитальных затрат на один процент и на
процентов при увеличении трудовых затрат
на один процент.
5
28. 6
Возможны и другие линеаризуемые функциидля построения множественной регрессии
3. Экспоненциальная
y e
a b1 x1 b 2 x 2 ... b n x n
.
Экспоненциальная форма используется как
правило для моделирования временного
изменения изучаемой величины. Например,
данные о расходах на продукты питания в США в
период с 1959 по 1983 гг. приводят к следующей
зависимости
y e
4 ,58 0 ,020 ( t 1959 )
.
29. 7
Смысл регрессионных коэффициентов здесьсостоит в том, что расходы на питание за
изучаемый период росли с темпом 2% в год. Это
становится очевидным. Если вычислить
эластичность расходов на питание по времени.
4 Гиперболическая регрессия.
y
a b1 x1 b 2 x 2 ... b n x n
1
a b1 x1 b 2 x 2 ... b n x n
.
Гиперболическая форма регрессионной кривой
используется при обратной связи признаков. Так, если
Y - объем плановых инвестиций, а X - норма
процента, то между ними существует связь, которая
может быть выражена в форме Y=a+b/X.
30. 8
Экспоненциальная форма сводится к линейнойтакже простым логарифмированием. Вычисляя
логарифм правой и левой частей уравнения
y e
получаем
a b1 x1 b 2 x 2 ... b n x n
8
.
ln y a b1 x1 b 2 x 2
... b n x n .
Обозначив LN Y =Z снова получаем линейную модель
31. 9
В случае гиперболической регрессионной моделилинеаризация модели также производится простой
заменой объясняемой переменной. Введем новую
переменную Z=1/Y. тогда вместо гиперболической
получаем линейную зависимость для новой
переменной
1
Z a b1 x1 b 2 x 2
y
... b n x n .
32. 10
Наконец, если исследователя не устраивает ниодин из вариантов рассмотренных выше функций
регрессии, то можно воспользоваться любыми
другими функциями, которые с помощью замен
переменных сводятся к линейным. Например, может
использоваться такая регрессионная модель
1
y a b1 x1 b 2
x2
b3 x
.
0,5
b 4 ln x 4 .
33. 11
Вводя переменные1
z1 x1 , z2
,
x2
11
z3 x , z 4 ln x 4
снова возвращаемся к линейной модели.
Естественно, что после анализа
линеаризованной модели нужно вернуться к
исходным переменным.
Очевидно, что при построении такой сложной
модели скорее всего придется встретиться с
проблемами ее интерпретации.
34. 4.3 Точечная оценка параметров множественной регрессии
35. 1
Если выполняются условия 1-6 применимостиметода МНК, то параметры уравнения
множественной регрессии определяются из
системы нормальных уравнений. Если
регрессионное уравнение имеет вид
y a b1 x1 b 2 x 2
... b n x n .
то система нормальных уравнений может
быть записана в виде
36. 2
y na b1 x1 b 2 x 2... b k x k ;
2
yx1 a x1 b1 x1 b 2 x 2 x1
... b k x k x1;
2
.......... .........
yxk a xk b1 x1xk
2
... b k x k .
b 2 x 2 xk
37. 3
Решение нормальной системы МНК может бытьнайдено с помощью метода определителей
Крамера. Чаще всего для решения системы
нормальных уравнений метода МНК используют
компьютерные программы, например Excel. Здесь
для этих целей можно использовать функцию
ЛИНЕЙН () из набора стандартных статистических
функций и функцию Регрессия из пакета анализа.
Применение этих функций для решения
уравнений будет продемонстрировано на
практических занятиях.
38. 4
Возможен и иной подход к построению уравнениямножественной регрессии. В этом случае все
переменные вначале заменяются стандартизованными отклонениями от соответствующих средних
значений:
y y
x1 x1
ty
, t x1
,
y
x1
t xk
xk xk
.
xk
39. 5
Средние значения всех введенных величинравны нулю, а дисперсия равна единице.
Для стандартизованных переменных
линейное регрессионное уравнение запишется
в виде
t y 1 t x1 2 t x 2
... k t x k .
обратим внимание также на то, что свободный
член в этом уравнении равен нулю.
5
40. 6
Регрессионные параметры в стандартизованноймодели находятся из системы уравнений МНК,
где в качестве коэффициентов при неизвестных
фигурируют частные коэффициенты
корреляции.
41. 7
ryx1 1 2 rx2 x1 ... k rx k x17
;
ryx2 1rx1x2 2 ... k rx k x2 ;
...................
ryxk 1rx1xk 2 rx2 xk ... k .
Преимуществом стандартизованной формы
уравнения регрессии является то, что теперь
коэффициенты уравнения сравнимы между собой
по величине и можно отбрасывать те переменные,
которые входят в уравнение с малым весом.
42. 8
Стандартизованные коэффициенты регрессии iкоэффициенты «чистой» регрессии bi связаны
между собой очевидным соотношением
bi i
σy
σ xi
,
a y b1 x1 b2 x2 ... bk xk .
пользуясь этими формулами можно переходить
от стандартизованной записи к обычной и
обратно.
8и
43. 4.4 Коэффициенты детерминации и множественной корреляции
44. 1
Практическая значимость уравнениямножественной регрессии оценивается с помощью
показателя множественной корреляции R или его
квадрата - коэффициента детерминации (R2).
Независимо от формы связи (линейная или
нелинейная) показатель детерминации находится
из уравнения
n
ESS
R 1
1
TSS
( yi
i 1
n
T 2
yi )
.
( yi y )
i 1
2
45. 2
Если используется уравнение регрессии встандартизованной форме, то можно легко
показать (см. Эконометрика под ред. Елисеевой
стр. 114-115), что
R
k
r
.
xi yxi
i 1
2
46. 3
Для определения коэффициентовмножественной корреляции и детерминации
используется остаточная (необъясненная)
дисперсия.
Ясно, что если число параметров уравнения
регрессии увеличится, то и ошибка уменьшится.
В пределе, если число параметров равно
числу наблюдений, то можно добиться полного
совпадения эмпирических и теоретических
(определяемых по уравнению регрессии)
результатов.
3
47. 4
Чтобы избежать необоснованного завышениякачества регрессионной модели при добавления
новой переменной вводится скорректированный
индекс множественной детерминации.
Скорректированный фактор детерминации
использует не просто отношение ESS/TSS, а
отношение этих величин, приходящихся на одну
степень свободы
ESS /( n m 1 )
R норм 1
TSS /( n 1 )
n 1
m- число
2
1 (1 R )
.
параметров при
n m 1
переменных x.
2
переменных x.
4
48. 5
Рассмотрим пример использованиянормированного фактора детерминации для
решения вопроса о включении в модель
дополнительной переменной.
Обратимся вновь к данным связи ВНП с
объемом потребления и объемом инвестиций
за 10 лет (млрд. долл.) см. след. слайд
49. 6
Данные о связи ВНП с объемом потребленияи объемом инвестиций за 10 лет (млрд. долл.)
6
ВНП
14
16
18
20
23
23,5
25
26,5 28,5 30,5
х1
8
9,5
11
12
13
14
15
16,5
17
18
1,65 1,8
2,0
2,1 2,2
2,4
2,65 2,85
3,2
3,55
х2
50. 7
Построим однофакторную регрессионнуюмодель связи ВНП и объема потребления и с
помощью функции Регрессия Пакета
анализа выведем данные регрессионной
статистики.
7
Регрессионная статистика
Множественный R
0,9939
R-квадрат
0,9878
Нормированный R-квадрат
0,9863
Стандартная ошибка
0,6345
Наблюдения
10,0000
51. 8
Включим теперь в число факторов регрессионной 8модели переменную Х2 – объем инвестиций. Как
следует из приведенных результатов, при этом
фактор детерминации вырос, а нормированный
фактор детерминации упал. Поэтому второй фактор в
регрессионную модель включать не следует.
Регрессионная статистика
Множественный R
0,9942
R-квадрат
0,9885
Нормированный R-квадрат
0,9852
Стандартная ошибка
0,6596
Наблюдения
10,0000
52. 9
Рассмотрим еще и однофакторную модель связи 9ВНП с объемом инвестиций Y(X2). Сравнивая
результаты, видим, что в этом случае величина
нормированного фактора вырастет при включении в
модель переменной Х1 . Таким образом, мы
показали, что в рассматриваемом случае связь
однофакторная Y=f ( X1)
Регрессионная статистика
Множественный R
0,9686
R-квадрат
0,9382
Нормированный R-квадрат
0,9305
Стандартная ошибка
1,4289
Наблюдения
10,0000
53. 4.5. Коэффициент частной корреляции
54. 1
Определим понятие коэффициента частнойкорреляции.
1
Частные коэффициенты (или индексы)
корреляции характеризуют тесноту связи между
результатом (Y) и соответствующим фактором
(xi) при устранении влияния других факторов.
Если говорить точнее, то частные коэффициенты
корреляции представляют собой отношение
сокращения остаточной дисперсии за счет
включения дополнительной переменной, к
остаточной дисперсии, имевшей место до
включения переменной в модель.
55. 2
Для простоты сначала рассмотрим случайдвухфакторной модели Y=f(x1 , x2 ). Остаточная
дисперсия при включении первого фактора в модель
n
2
S yx1
( yi
i 1
T
2
yi ( x1 ))
n
.
56. 3
При включении двух факторов остаточнаядисперсия будет равна
n
2
S yx1x2
( yi
i 1
T
yi ( x1 , x2
2
))
.
n
Следовательно влияние включения второго
фактора на результат Y можно определить как
ryx2 ,x1
2
S yx1
2
S yx1x2
2
S yx1
.
3
57. 4
Если вспомнить определение коэффициентадетерминации
n
2
R 1
( yi
i 1
n
T 2
yi )
,
( yi y )
i 1
ryx2 ,x1
2
4
то легко увидеть, что
коэффициент частной
корреляции в
рассматриваемом
случае может быть
записан в виде
2
1 R yx1x2
1
2
1 R yx1
.
58. 5
модельВ общем случае, когда рассматривается
с k факторами коэффициент частной корреляции,
измеряющий влияние на y фактора xi
записывается в виде
ryxi ,x1x2 ...xi 1xi 1 ...xk
2
1 R yx1 ...xi ...xk
1
2
1 R yx1 ...xi 1xi 1 ..xk
.
59. 6
Рассмотрим пример использования факторачастной корреляции для обоснования
необходимости включения дополнительного
фактора в модель.
6
Рассмотрим статистические данные о потреблении
текстиля (текстильных изделий) в Голландии в
период между двумя мировыми войнами с 1923 по
1939 годы. В приведенной ниже таблице T реальное потребление текстиля на душу населения,
DPI - реальный располагаемый доход на душу
населения, P - относительная цена текстиля. Все
показатели выражены в индексной форме, в
процентах к 1925 году.
60. 7
Данные о реальном потребление текстиля взависимости от располагаемого дохода Х1 и цен
на текстиль Х2
Год
1923
1924
1925
1926
1927
1928
1929
1930
1931
T
99,2
99
100
111,6
122,2
117,6
121,1
136
154,2
DPI
96,7
98,1
100
104,9
104,9
109,5
110,8
112,3
109,3
p
101
100
100
90,6
86,5
89,7
90,6
82,8
70,1
Год
1932
1933
1934
1935
1936
1937
1938
1939
T
153,6
158,5
140,6
136,2
168
154,3
149
165,5
DPI
105,3
101,7
95,4
96,4
97,6
102,4
101,6
103,8
7
p
65,4
61,3
62,5
63,6
52,6
59,7
59,5
61,3
61. 8
Построим степенную регрессионную модель илинеаризуем ее. Для этого достаточно вычислить
десятичные логарифмы исходных переменных.
Для новых переменных построим линейную
регрессионную модель, используя функцию
Регрессия из Пакета анализа. В результате
получаем следующее регрессионное уравнение
lg T 1.374 1.143 lg DPI 0.829 lg P .
Для этой модели значение параметра R2 =0,974, а
сумма квадратов остатков ESS = 0,00256.
62. 9
Исключим теперь переменную lg DPI изрегрессионного уравнения и найдем уравнение
однофакторной регрессии. В результате получаем
уравнение регрессии
lg T 3,564 0,770 lg P,
для которого значение R2=0,876, а сумма остатков
ESS=0,0124.
63. 10
Найдем на основании этих данныхкоэффициент частной корреляции
ryx1 ,x2
2
1 R yx1x2
1
2
1 R yx2
1 0,974
1
0,890.
1 0,876
Таким образом, коэффициент частной корреляции
оказался высок и переменную следует включить в
модель.
64. 11
Обратим внимание на то, что линейныйкоэффициент корреляции между lg T и lg DPI
весьма мал и составляет всего 0,098.
Тем не менее частный коэффициент
корреляции lg T и lg DPI при фиксированном
значении lg P оказался весьма высок. Таким
образом, далеко не всегда можно отбирать
переменные для включения в модель только
основываясь на данных о линейном
коэффициенте корреляций между переменными.
65. 4.6. Оценка надежности результатов множественной регрессии и корреляции
66. 1
Значимость уравнения множественнойрегрессии в целом, так же как и парной регрессии
оценивается с помощью F - критерия Фишера.
QR ( n m 1 )
F
.
QE m
Обратим внимание на то, что буквой m здесь
обозначено число факторов, включенных в модель, а
не число параметров регрессионной модели.
Учитывая определение фактора множественной
детерминации
QE QR
R 1
QT QT
2
67. 2
Выразим величины QE иQR
через
2
R2
2
2
QE ( 1 R )QT ; QR R QT .
и подставим полученные уравнения в определение
показателя Фишера. В итоге получаем
F
2
R ( n m 1)
2
(1 R ) m
.
Таким образом, для нахождения значимости
регрессионной модели достаточно вычислить
коэффициент множественной детерминации R2, а
затем по приведенной выше формуле найти
коэффициент Фишера.
68. 3
Дальнейшая оценка значимости производится 3точно также, как и в случае однофакторной
регрессии. Наряду с эмпирическим значением
критерия Фишера, которое определяется
приведенной выше формулой определяется
критическое значение показателя Фишера при
заданных числах степеней свободы k1=m, k2=n-m-1
и заданном уровне значимости . В Excel
критическое значение статистики Фишера можно
найти, вызвав функцию FРАСПРОБР ( k1, k2) и
передав ей параметры: уровень значимости, число
степеней свободы k1 и степеней свободы k2 .
69. 4
Если Fэмпир > Fкритич , то гипотеза о не значимостиуравнения регрессии отвергается.
Можно оценивать не только значимость
уравнения регрессии в целом, но и значимость
фактора, дополнительно включенного в
регрессионную модель.
Необходимость такой оценки связана с тем,
что не каждый фактор, вошедший в модель,
существенно увеличивает долю объясненной
вариации результативного признака.
Кроме того при наличии в модели нескольких
факторов они могут вводиться в модель в разной
последовательности.
70. 5
Ввиду корреляции между факторами значимостьодного и того же фактора может разной в
зависимости от очередности его введения в
модель.
Частный F - критерий построен на сравнении
прироста факторной дисперсии, обусловленной
влиянием дополнительной переменной. Если
оценивается влияние фактора xk после того как
в модель были введены факторы x1 …xk-1 то
формула частного F - критерия примет вид
71. 6
FxkR
2
yx1 ...xk
R
1 R
2
2
yx1 ...xk 1
yx1 ...xk
n m 1 6
.
1
В числителе формулы стоит прирост доли
объясненной вариации за счет включения в модель
переменной хк , а в знаменателе доля остаточной
дисперсии при включении в модель всех факторов.
Так как прирост факторной суммы обеспечен
дополнением одной переменной, то число степеней
свободы для этой величины равно единице. Для
суммы квадратов отклонений остатков не
объясняемых регрессией число степеней свободы
равно n-m-1
72. 7
Эмпирическое значение частного F - критериясравнивается с критическим при числах степеней
свободы k1=1, k2=n-m-1 и уровне значимости .
Пример
По данным статистических наблюдений в США
требуется построить модель связи между
расходами на продукты питания (Y)
располагаемым личным доходом Х1
и индексом цен на продукты питания x2.
Данные (в индексной форме) приведены на
следующем слайде.
73. 8
Статистические данные о связи расходов на продукты питания (Y)располагаемым личным доходом Х1 и индексом цен на продукты питания x2
Год
1959
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
Y
99,7
100,9
102,5
103,5
104,6
108,8
113,7
116,6
116,6
123,4
125,9
129,4
130,0
8
X1
X2
Год
Y
X1
X2
479,7 97,7 1972 132,4 810,3 100,0
489,7 97,1 1973 129,4 865,3 108,1
503,8 97,2 1974 128,1 858,4 112,5
524,9 96,9 1975 132,3 875,8 111,9
542,3 96,8 1976 139,7 906,8 108,9
580,8 97,1 1977 145,2 942,9 107,4
616,3 97,8 1978 146,1 988,8 110,6
648,8 100,0 1979 149,3 1015,5 112,2
673,5 98,3 1980 153,2 1021,6 109,8
701,3 98,2 1981 153,0 1049,3 109,7
722,5 99,0 1982 154,6 1058,3 107,8
751,6 100,0 1983 161,2 1095,4 106,0
779,2 98,3
74. 9
Используя функцию ЛИНЕЙН ( ) найдемЗначения факторов детерминации для
Одномерной модели Y=f(x2 )
Y=f(x2)
2,475 -127,348
0,407
42,070
0,616
11,921
36,961
23,000
5252,864 3268,766
9
75. 10
Приведенные результаты позволяютпостроить регрессионную модель
y 127,348 2,475 x 2
с фактором детерминации
R
2
yx2
0 ,616.
76. 11
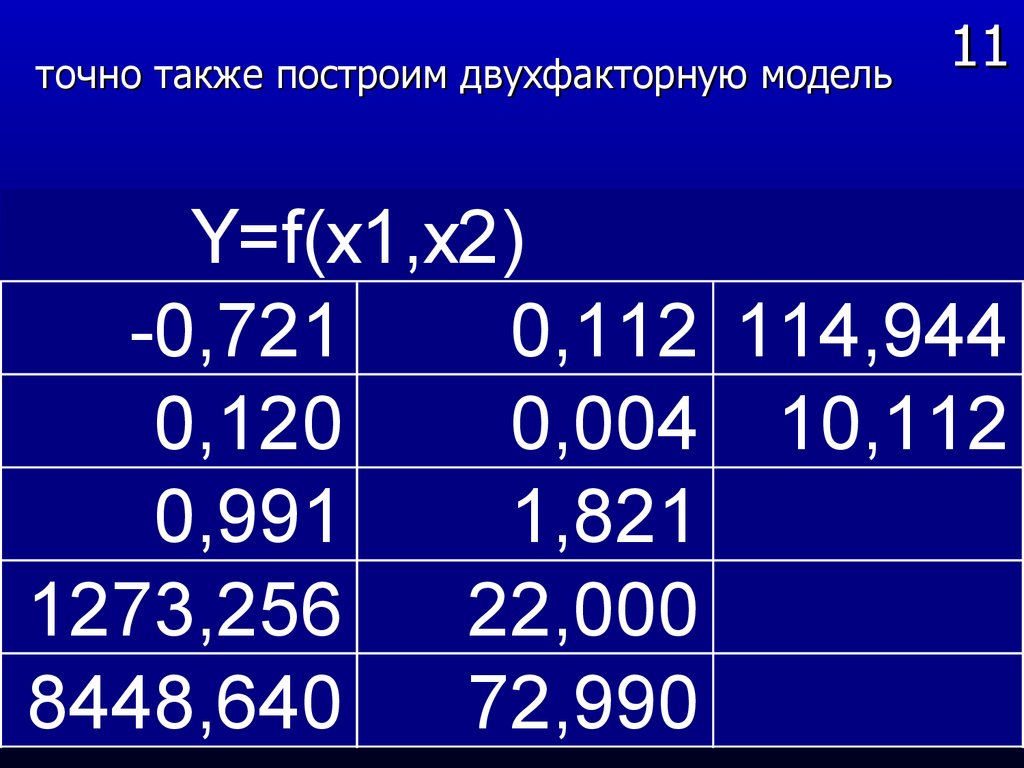
точно также построим двухфакторную модель11
Y=f(x1,x2)
-0,721
0,112 114,944
0,120
0,004 10,112
0,991
1,821
1273,256
22,000
8448,640
72,990
77. 12
Регрессионное уравнение в этом случае имеетвид
y 114,94 0,112 x1 0,721 x 2 ,
а значение фактора детерминации равно
R
Fx1
R
2
2
yx1x2
1 R
yx1x2
R
2
2
0,991.
yx2
yx1x2
25 2 1
963,2.
1
Поскольку при уровне значимости 0,05 Fкрит = 4,3, то
частный коэффициент
F
значим.
78. 13
Если вначале включить в модель переменную x1,а затем попытаться включить переменную x2 , то
получим результат
Fx2
R
2
yx1 x2
1 R
R
2
2
yx1 x2
yx1
25 2 1
1
0,991 0,977
22 35,9.
1 0,991
Следовательно этот частный коэффициент F
также значим.
79. 4.7. Оценка значимости коэффициентов множественной регрессии
80. 1
Оценка статистической значимостикоэффициентов уравнения множественной
регрессии производится по стандартным формулам
математической статистики. При этом выдвигается
гипотеза, что соответствующий коэффициент в
действительности равен нулю. Тогда оценивается
величина
tbi
bi
mbi
,
имеющее распределение Стьюдента, где
mb
среднеквадратическое отклонение
соответствующего регрессионного коэффициента.
81. 2
Затем оценивается критическое значениестатистики Стьюдента при заданном уровне
значимости и если tрасчет > tкритич то нулевая
гипотеза отвергается и коэффициент признается
статистически значимым.
Если не пользоваться вспомогательными
пакетами анализа, то требуется достаточно
большой объем вычислений для ответа на
вопрос о статистической значимости всех
коэффициентов множественной регрессионной
модели. Более того, эти вычисления следует
выполнять используя матричные обозначения,
что для начинающих изучать эконометрику
представляет дополнительные сложности.
2
82. 3
По этой причине будем исходить из того, что 3для анализа значимости коэффициентов регрессии
используются вспомогательные математические
пакеты, например Excel.
Как уже указывалось, среди стандартных функций
статистического анализа Excel содержит и функцию
ЛИНЕЙН () которая возвращает, в частности
регрессионные коэффициенты (первая строка) и
стандартные ошибки (среднеквадратические
отклонения) для них – вторая строка. Пользуясь
этими результатами уже нетрудно оценить
статистическую значимость каждого из
коэффициентов.
83. 4
Более полную информацию дает использованиефункции Регрессия из Пакета анализа.
Приведем неполный фрагмент выдачи, которую
возвращает эта функция для статистических
данных о связи расходов на продукты питания (Y)
располагаемого личного дохода (Х1) и индекса
цен на продукты питания (x2)
84. 5
Дисперсионный
анализ
Регрессия
Остаток
Итого
df
2
22
24
Значи
SS
MS
F
мость
F
8448,6 4224,3 1273,3
0,00
73,0
3,3
8521,6
5
5
Коэфф Станда
tPНижни Верхни
ициент ртная статис Значе
е 95% е 95%
ы
ошибка тика
ние
Yпересечен
ие
Переменн
ая X 1
Переменн
ая X 2
114,9
10,1 11,4
0,1
0,0 31,0
0,0
0,1
0,1
0,1
0,0
-1,0
-0,5
-0,7
-6,0
0,0 94,0 135,9
85. 6
Для оценки статистической значимости6
коэффициентов множественной регрессии можно
использовать и частный F – критерий. Можно
показать, что
tbi Fxi .
Иначе говоря t -критерий для коэффициента
регрессии в i-том факторе определяется корнем
квадратным из величины частного F -критерия для
этой величины.
Этот результат легко можно проверить, используя
данные данные о связи расходов на продукты питания
(Y) располагаемым личным доходом Х1 и индексом
цен на продукты питания x2
86. 7
Действительно, вспоминая данные о частныхкоэффициентах корреляции
Fx1 963,2;
Fx1 31,03;
Fx2 35,9;
Fx2 5,99.
Как следует из данных приведенных на слайде 84,
именно эти значение имеет t -критерий для
коэффициентов b1 и b2 .
7
87. Методы обнаружения гетероскедастичности остатков
88. 1
Для обнаружения гетероскедастичности(неодинаковости разброса данных для различных
точек наблюдения) можно использовать либо
графический метод, либо один из возможных
тестов.
В простейшем случае гетероскедастичность
можно заметить непосредственно, построив поле
корреляции переменных и линию тренда. Такой
пример приведен ниже.
89. 2
Модельные данные для демонстрации2
гетероскедастичности. Линия тренда изображена
красным цветом
800
700
600
500
400
300
200
100
0
500,00
1000,00 1500,00 2000,00 2500,00 3000,00 3500,00
90. 3
На практике для графического обнаружениягетероскедастичности по оси абсцисс откладывают
значение результативной переменной, получаемой из
уравнения регрессии, а по оси ординат либо ошибку,
либо квадрат ошибки для соответствующей точки.
На слайде ниже представлена такая диаграмма,
которая получена на основании данных о
деятельности крупнейших компаний США за 1996 г.
91. 4
Данные о финансовой деятельности компаний№ п/п
Использован
Чистый
ный капитал.
доход, млрд.
млрд. долл.
долл. США
США.
№ п/п
4
Чистый
Использованн
доход,
ый капитал.
млрд. долл. млрд. долл.
США
США.
1
2
3
4
5
6
7
8
1,5
1,6
3
1,8
1,4
2,4
2,4
3,6
5,9
6,4
6,5
6,5
9,3
11,2
12,5
13,3
11
12
13
14
15
16
17
18
1,6
3
0,9
2,4
2,7
5,5
0,1
4,2
15,8
16,4
18,9
22,7
25,4
27,1
29,6
32,5
9
10
3,3
3,3
14,3
15,4
19
20
6,5
6,6
50,4
83,6
92. 5
Гетероскедастичность данных предыдущегослайда. По оси Y отложена ошибка
5
3
2
1
0
-1 1,5
-2
-3
-4
3,5
5,5
7,5
93. 6
Для аналитической проверки данных нагетероскедастичность чаще всего используют
тест Голдфелда - Квандта.
6
Для проведения теста Голдфелда -Квандта вся
совокупность делится на три подвыборки с
объемами k , (n-2k), k. В нашем случае 7, 6, 7.
Далее выдвигаем гипотезу об отсутствии
гетероскедастичности и вычисляем сумму
квадратов отклонений ESS для первой и третьей
выборок (это можно сделать с помощью функции
ЛИНЕЙН в Excel).
94. 7
Для сравнения соответствующих дисперсий строитсяследующая F - статистика
ESS3 k m 1
F
.
ESS1 k m 1
Эта величина распределена по закону Фишера с
числами степеней свободы k-m-1, k-m-1. Если
фактическое значение критерия больше
критического, то гипотеза об отсутствии
гетероскедастичности отклоняется.
95. 8
Используем этот тест для оценкигетероскедастичности зависимости прибыли от
использованного капитала.
8
Упорядочим исходные данные по увеличению
факторного признака.
Проверяется по существу гипотеза , что с ростом
факторного признака возрастает и ошибка.
Находим суммы квадратов ошибок для первой и
последней трети данных, используя функцию
линейн().
96. 9
В итоге получаем:Данные для первой
трети набора
0,06
0,1
0,08
0,45
0,18
ESS1
1,47894
0,82877
0,62472
5
1,95135
9
Данные для последней
трети набора
0,0724
0,037392
0,428505
3,748985
14,89484
ESS3
1,194
1,633
1,993
5
19,87
97. 10
Поскольку фактическое значение статистикиF=10,18, а критическое значение при уровне
значимости 0,05 и числах степеней свободы к1 =7,
к2 =7
равно 5,05, то гипотезу об отсутствии
гетероскедастичности отвергаем.
Следовательно метод наименьших квадратов не
может гарантировать нахождение наилучших
параметров кривой регрессии.



































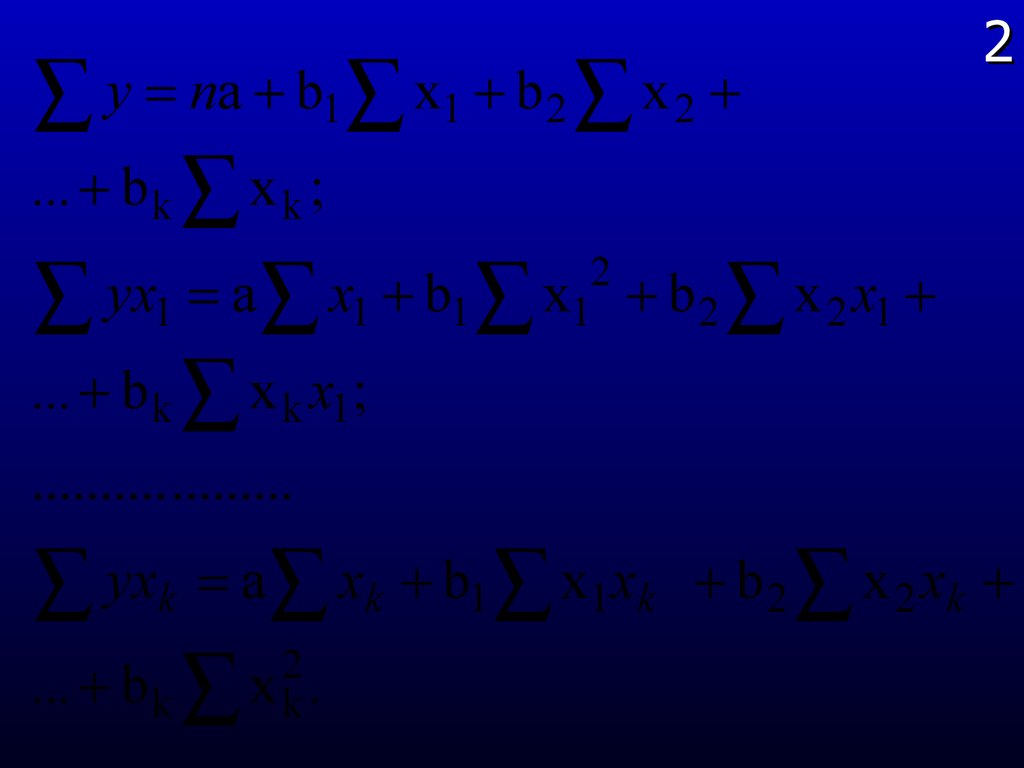
























































 mathematics
mathematics








