Similar presentations:
Множественная регрессия и корреляция
1. Множественная регрессия и корреляция
2.
1. Отбор факторов и выбор формы уравнения2. Оценка параметров уравнения множественной регрессии
3. Показатели силы связи в модели множественной
регрессии
4. Показатели тесноты связи
5. Оценка достоверности построенного уравнения
6. Использование фиктивных переменных в моделях
регрессии
7. Проблемы, возникающие при построении регрессионных
моделей: мультиколлинеарность и гетероскедастичность
3.
Основнаяпостроение
цель
модели
y f ( x1 , x 2 ,..., x p ) ,
множественной
с
регрессии
несколькими
определив
при
–
факторами
этом
влияние
каждого из них в отдельности и совокупное их
воздействие на результат признаки)
4. При отборе факторов в уравнение множественной регрессии необходимо соблюдать следующее условия:
• в модель нужно включать только существенные факторы,непосредственно формирующее результат
• факторы должны быть количественно измерены
• факторы не должны находиться в тесной взаимосвязи друг
с другом (значение коэффициента корреляции между
факторами, входящими в модель должно быть менее 0,7)
5. Отбор факторов основан на:
• теоретическом анализе взаимосвязирезультата с кругом факторов
• количественном анализе (на основе
матрицы парных коэффициентов
корреляции, матрицы частных
коэффициентов корреляции)
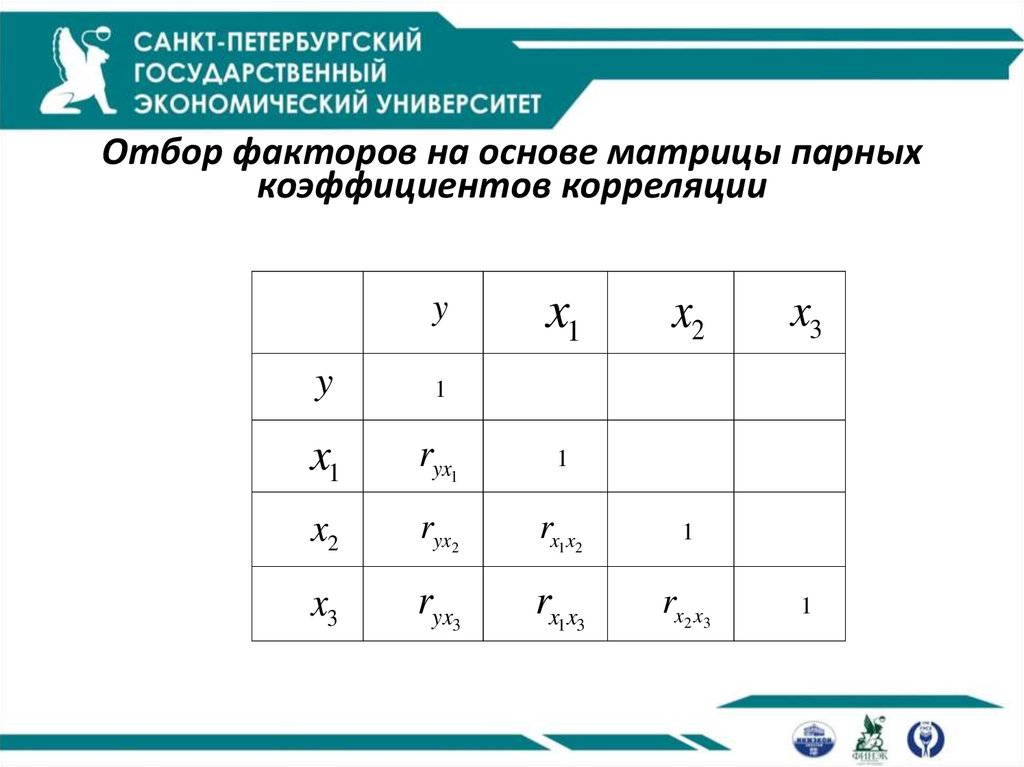
6. Отбор факторов на основе матрицы парных коэффициентов корреляции
yx1
x2
y
1
x1
ryx1
1
x2
ryx2
rx1x2
1
x3
ryx3
rx1x3
rx2 x3
x3
1
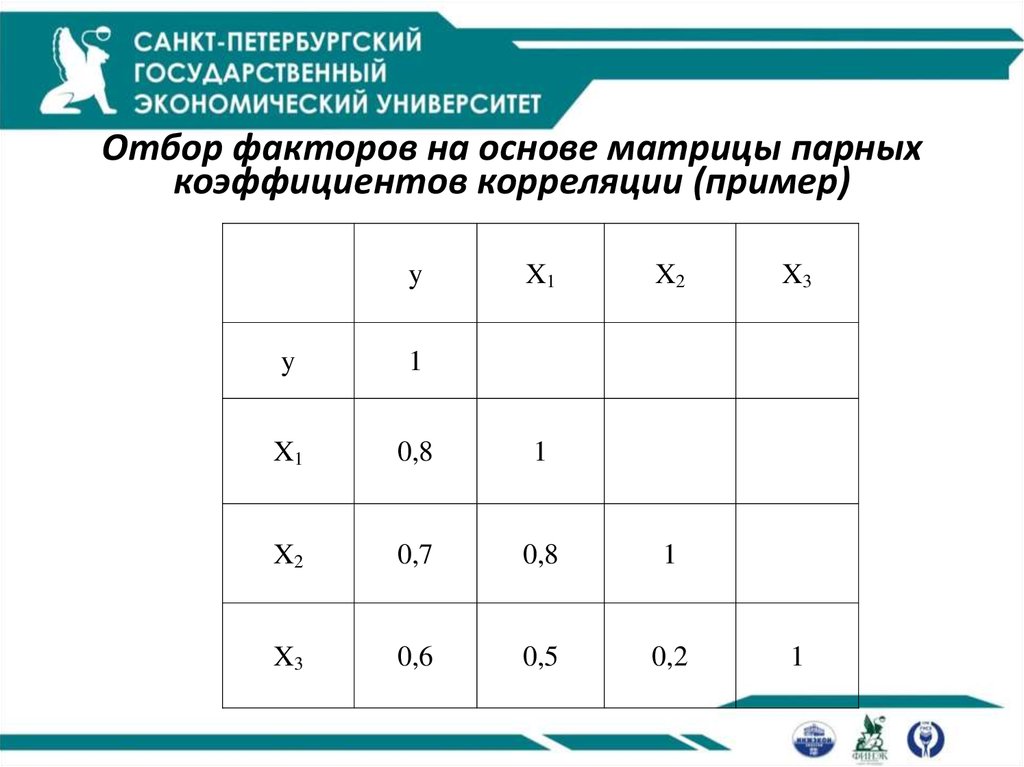
7. Отбор факторов на основе матрицы парных коэффициентов корреляции (пример)
yX1
X2
y
1
X1
0,8
1
X2
0,7
0,8
1
X3
0,6
0,5
0,2
X3
1
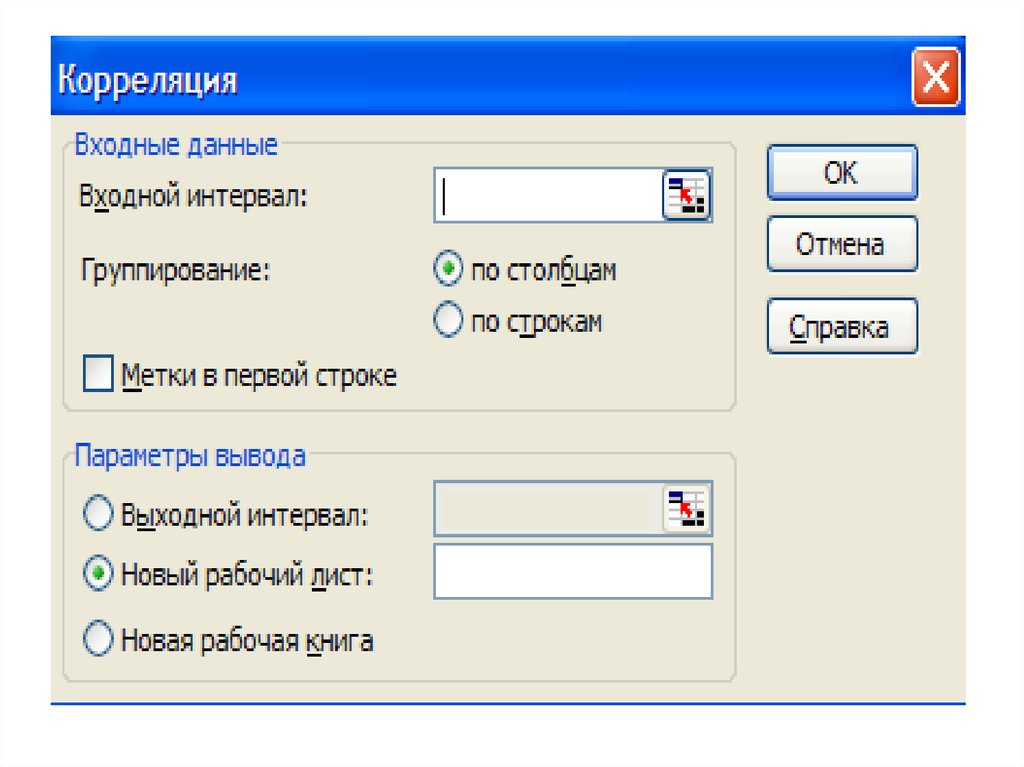
8. Использование Microsoft Excel для построения матрицы парных коэффициентов корреляции
• Анализ данных• Корреляция
В диалоговом окне «корреляция» задаются следующее параметры
–
Входной интервал – вводится ссылка на диапазон ячеек, содержащий
исходную информацию. Для этого надо выделить исходные данные,
записанные в лист Excel. Если данные выделяются с названием граф, то
устанавливается флажок метки.
– Параметры вывода: выходной интервал (вводится ссылка на любую
свободную ячейку на данном рабочем листе); другой рабочий лист или
другая рабочая книга.
• ОК
9.
10. Виды функций, наиболее часто используемые в эконометрическом моделировании
линейная y a b1 x1 b2 x 2 ... b p x p ;1
2
p
y
ax
x
...
x
1
2
p
степенная функция
;
b
b
b
1
2
p
y
ab
b
...
b
1
2
p
показательная функция
;
x
экспонента
гипербола
y e
y
x
x
a b1 x1 b2 x2 ... b p x p
1
a b1 x1 b2 x2 ... b p x p
;
.
11. Оценка параметров
• Для оценки параметров уравнения множественнойрегрессии применяют метод наименьших квадратов
(МНК). При этом нелинейные функции приводятся к
линейному виду по параметрам.
y a b1 x1 b2 x2
y na b1 x1 b2 x 2
2
yx1 a x1 b1 x1 b2 x1 x 2
2
yx 2 a x 2 b1 x1 x 2 b2 x 2
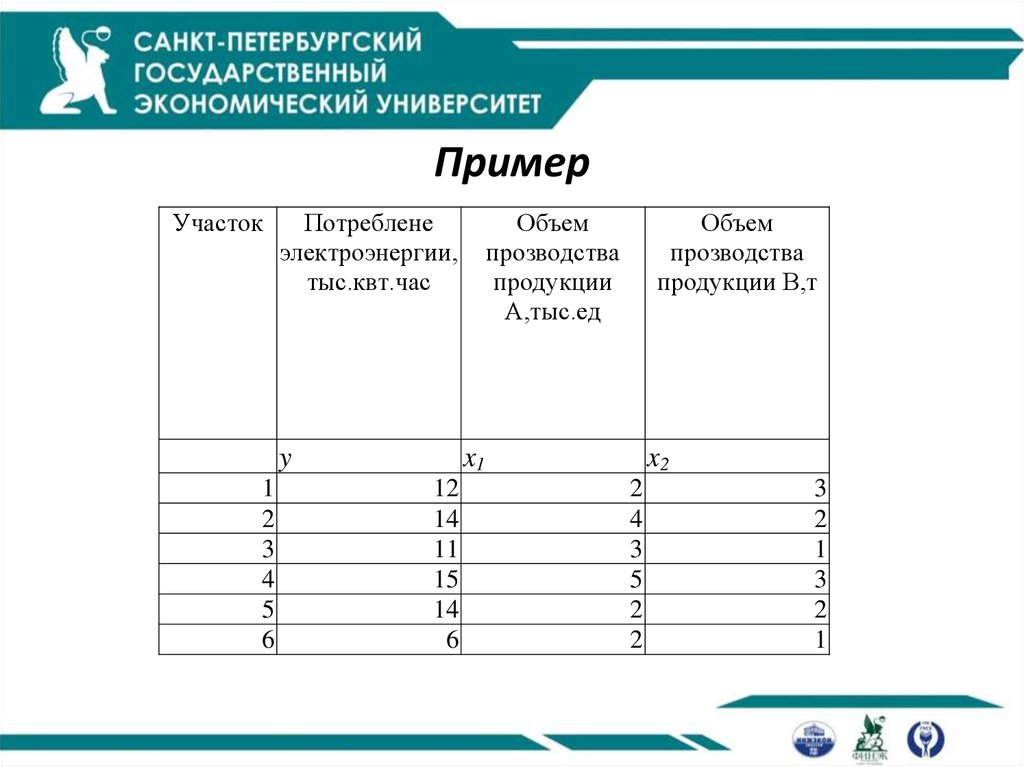
12. Пример
УчастокПотреблене
электроэнергии,
тыс.квт.час
y
1
2
3
4
5
6
Объем
прозводства
продукции
А,тыс.ед
Объем
прозводства
продукции В,т
x1
12
14
11
15
14
6
x2
2
4
3
5
2
2
3
2
1
3
2
1
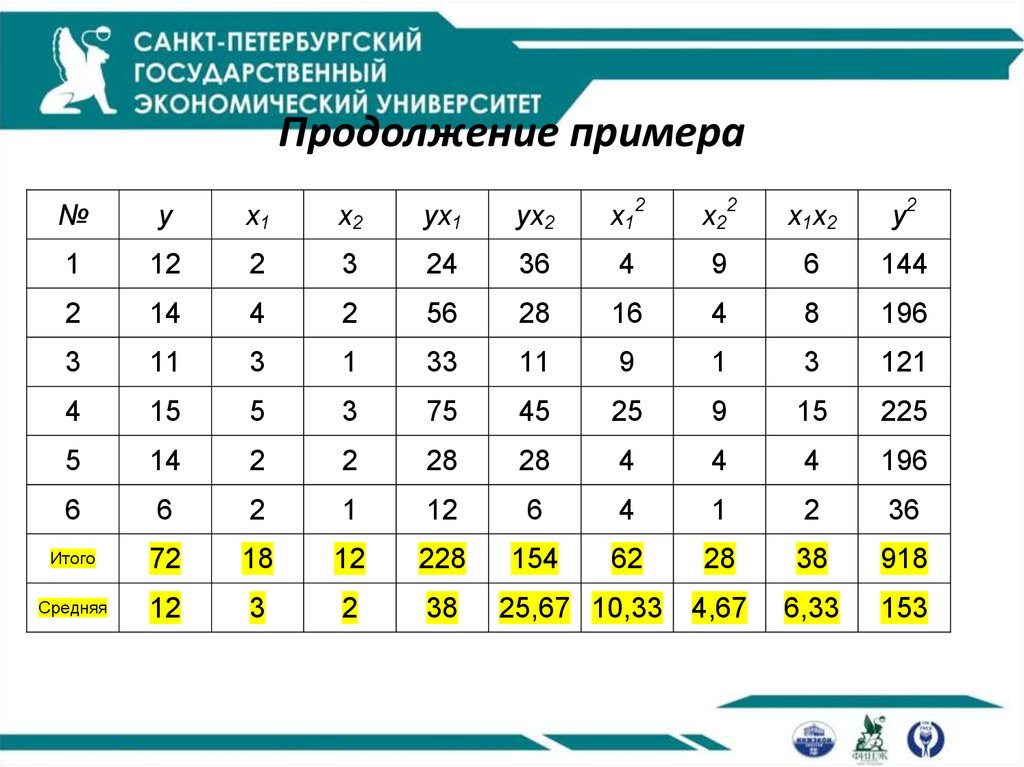
13. Продолжение примера
№y
x1
x2
yx1
yx2
x12
x22
x1x2
y2
1
12
2
3
24
36
4
9
6
144
2
14
4
2
56
28
16
4
8
196
3
11
3
1
33
11
9
1
3
121
4
15
5
3
75
45
25
9
15
225
5
14
2
2
28
28
4
4
4
196
6
6
2
1
12
6
4
1
2
36
Итого
72
18
12
228
154
62
28
38
918
Средняя
12
3
2
38
4,67
6,33
153
25,67 10,33
14. Продолжение примера
72 6a 18b1 12b2228 18a 62b1 38b2
154 12a 38b 28b
1
2
6 18 12
18 62 38 168
72 18 12
a 228 62 38 840
12 38 28
154 38 28
6 72 12
b1 18 228 38 168
6 18 72
b2 18 62 228 336
12 154 28
12 38 154
15. Продолжение примера
a 840a
5
168
b1 168
b1
1
168
b2 336
b2
2
168
y 5 x1 2 x2
16.
a y b1 x1 b2 x2ryx1 ryx2 rx1x2 y
b1
2
1 rx1x2
x1
ryx2 ryx1 rx1x2 y
b2
2
1 r x1x2
x2
17. Пример
y 5 x1 2 x218.
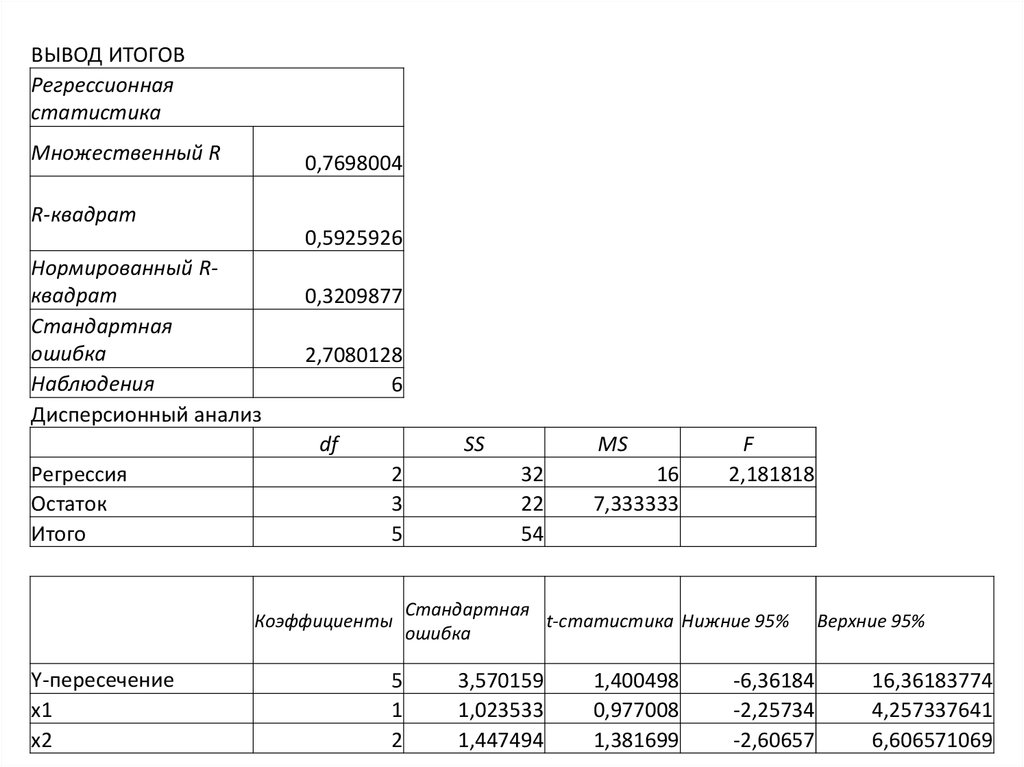
ВЫВОД ИТОГОВРегрессионная
статистика
Множественный R
0,7698004
R-квадрат
0,5925926
Нормированный Rквадрат
Стандартная
ошибка
Наблюдения
Дисперсионный анализ
0,3209877
2,7080128
6
df
Регрессия
Остаток
Итого
SS
2
3
5
Коэффициенты
Y-пересечение
x1
x2
5
1
2
MS
32
22
54
16
7,333333
F
2,181818
Стандартная
t-статистика Нижние 95%
ошибка
3,570159
1,023533
1,447494
1,400498
0,977008
1,381699
-6,36184
-2,25734
-2,60657
Верхние 95%
16,36183774
4,257337641
6,606571069
19. Показатели силы связи в модели множественной регрессии
• Абсолютные• Относительные
– Стандартизованные коэффициенты регрессии
– Частные коэффициенты эластичности
20. Абсолютные показатели силы связи
Показывают, на сколько единиц в среднем изменяетсярезультативный признак при изменении
рассматриваемого факторного признака на одну единицу
при условии, что остальные факторы зафиксированы на
среднем уровне и не меняются
21. Относительные показатели связи
частные коэффициенты эластичностиЭj bj
xj
y
стандартизованные
j bj
x
j
y
коэффициенты
регрессии
22. Стандартизованные коэффициенты регрессии (для двухфакторной модели)
12
ryx1 ryx2 rx1x2
1 r
2
x1 x2
ryx2 ryx1 rx1x2
1 r
2
x1 x2
;
.
23. Частные коэффициенты эластичности
показывают, на сколько процентов в среднем меняетсярезультативный признак при изменении рассматриваемого
факторного признака на один процент при условии, что
остальные факторы зафиксированы на среднем уровне и не
меняются.
Параметры
b1 , b2 ,..., b p
в
степенной
частными коэффициентами эластичности
модели
являются
24. Частные коэффициенты эластичности для линейной функции
Э j bj3
Э1 1 0, 25%
12
xj
y
2
Э2 2 0,33%
12
25. Коэффициент множественной детерминации
Коэффициент множественной детерминации ( R 2 )показывает долю вариации результативного признака, за
счет вариации включенных в модель факторов:
SS E
SS R
1
R
SST
SST
2
26. Продолжение примера
2y y y 153 12 9
2
2
SST 9 6 54
2
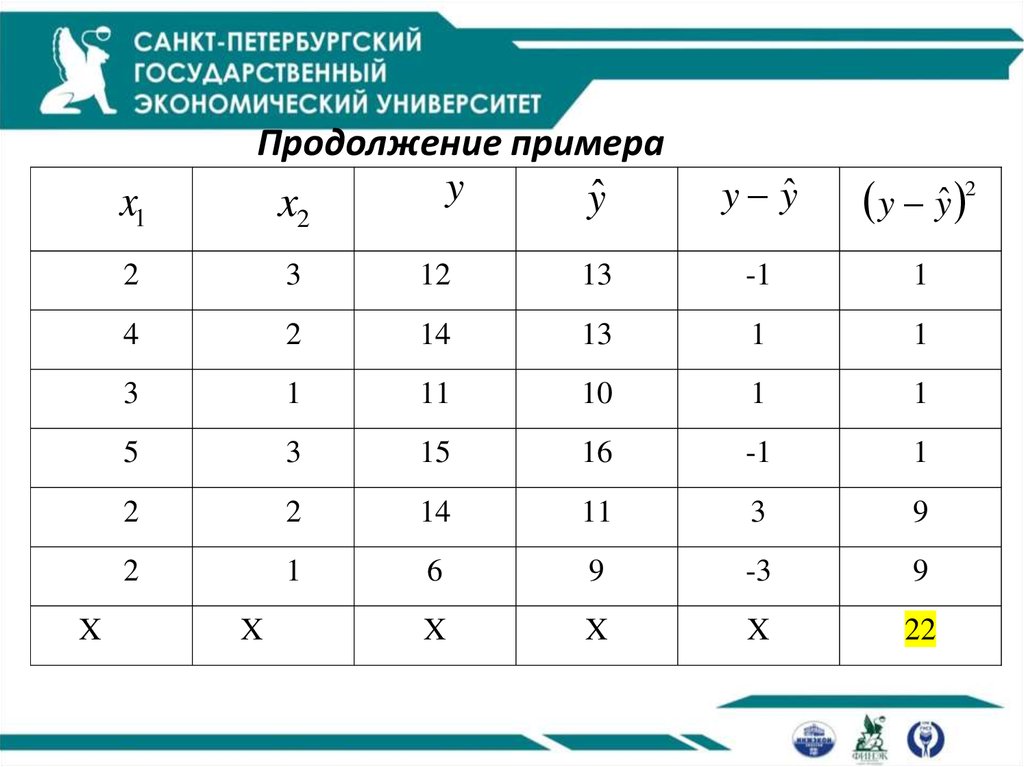
27. Продолжение примера
x1X
Продолжение примера
y
yˆ
x
2
y yˆ
y yˆ 2
2
3
12
13
-1
1
4
2
14
13
1
1
3
1
11
10
1
1
5
3
15
16
-1
1
2
2
14
11
3
9
2
1
6
9
-3
9
X
X
X
22
X
28. Продолжение примера. Расчет коэффициента детерминации для линейной функции
22R 1
0,593
54
2
29. Скорректированный коэффициент детерминации
2скорр.
R
2
Rñêîðð
SSост : (n m 1)
(n 1)
2
1
1 (1 R )
SSобщ : (n 1)
(n m 1)
6 1
1 1 0,593
0,322 32,2%
6 2 1
30. Коэффициент (индекс) множественной корреляции
Коэффициент (индекс) множественной корреляции(R)
–
корень
из
квадратный
множественной детерминации 0 R 1 :
R R
2
0 R 1
R 0,593 0,77
коэффициента
31. Коэффициент множественной корреляции
RRyx1x2
j
ryx j
ryx2 1 ryx2 2 2ryx1 ryx2 rx1x2
1 rx21x2
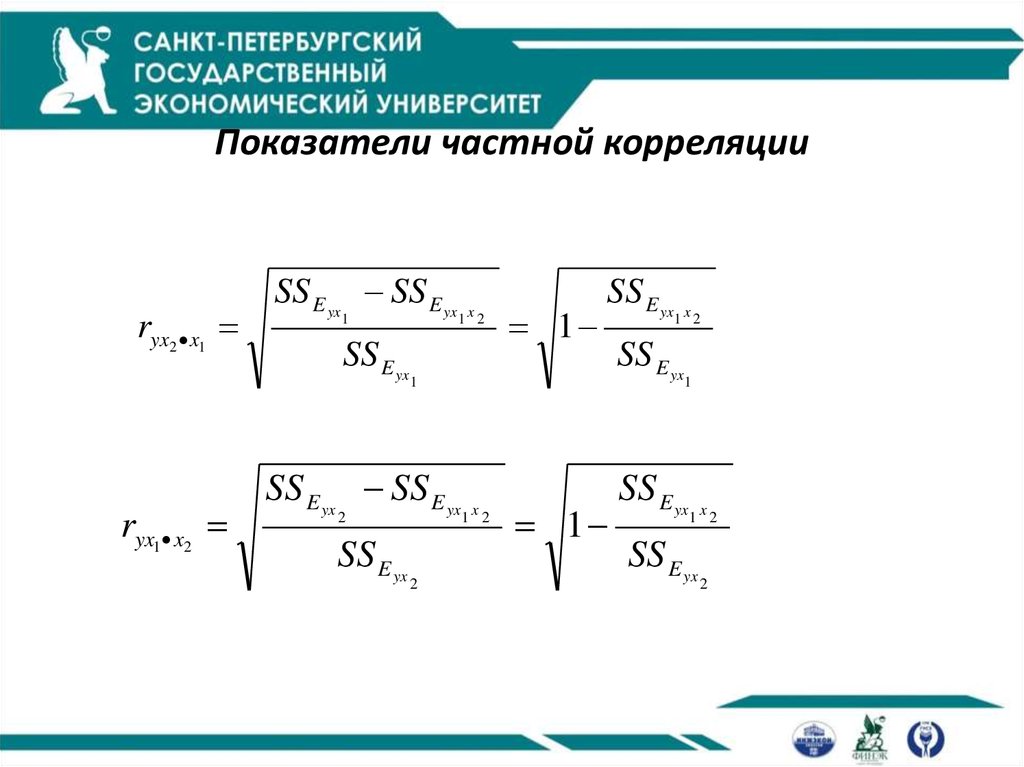
32. Показатели частной корреляции
основаны на соотношении сокращенияостаточной вариации за счет дополнительно
включенного в модель фактора к остаточной
вариации до включения в модель
соответствующего фактора
33. Показатели частной корреляции
ryx2 x1ryx1 x2
SS E yx SS E yx x
1
SS E yx
1 2
1
SS E yx SS E yx
2
SS E yx
1
SS E yx x
2
1x2
1
1 2
SS E yx
1
SS E yx
1x2
SS E yx
2
34. Показатели частной корреляции
ryx1 x2 1ryx1 x2
1 R
2
yx1 x2
2
yx2
1 r
ryx1 ryx2 rx1x2
1 r 1 r
2
yx2
2
x1x2
ryx2 x1 1
ryx2 x1
1 Ryx2 1x2
1 ryx2 1
ryx2 ryx1 rx1x2
1 r 1 r
2
yx1
2
x1 x2
35. Оценка достоверности модели
MS RR2 n m 1
F
2
MS E 1 R
m
0,593 6 2 1
F
2,18
1 0,593
2
Fтабл( 0,05;dfфакт 2;dfост 3) 9,55
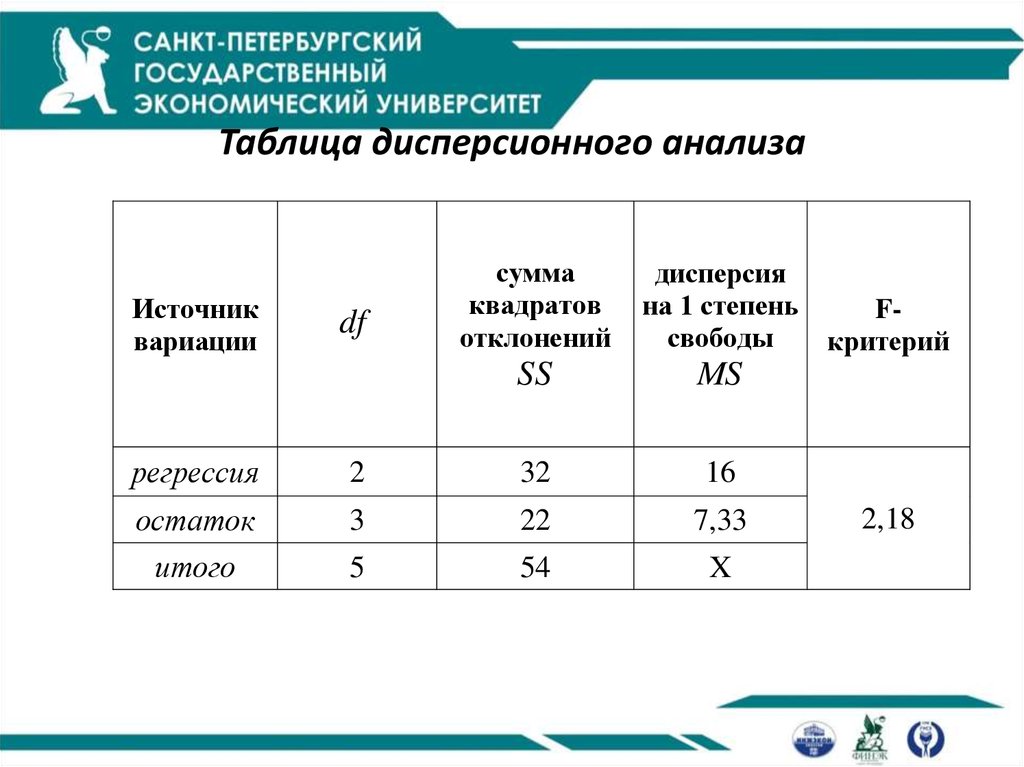
36. Таблица дисперсионного анализа
Источниквариации
df
сумма
квадратов
отклонений
дисперсия
на 1 степень
свободы
SS
MS
регрессия
2
32
16
остаток
3
22
7,33
итого
5
54
X
Fкритерий
2,18
37. Оценка достоверности параметров
bjtb j
где
Seb j
,
Seb j - случайная ошибка коэффициента условно чистой регрессии
y
Se b
x
j
j
1 R
1 Ryx2 1... x p
2
x j x1 ... x p
n m 1
bj
38. Оценка достоверности параметров
ySe b
x
1
1
1 Ryx2 1x2
1 r n m 1
Se b2 1,447
t b1 0,977
t b2 1,382
ttab. 3,18
2
x1x2
3
1,153
1 0,593
1,024
2
1 0,35 6 2 1
39. Доверительные интервалы для оцениваемых параметров
bj ttab.( ,df ) Seb j bj bj ttab.( ,df ) Seb jДоверительный интервал позволяет:
– Оценить значимость параметра (параметр будет значим, если в
доверительный интервал не входит ноль).
– Дать экономическую интерпретацию коэффициента регрессии (с
вероятностью (1-α) при единичном изменении независимой
переменной xj зависимая переменная у изменится не меньше,
чем на bj,min и не больше, чем на bj,max .
40. Критерии выбора наилучшей функции
• Минимальная доля остаточной дисперсии в общей дисперсии, то естьмаксимальная величина коэффициента детерминации R2. Если
модели регрессии содержат разное количество параметров, вместо R2
следует сравнивать скорректированные коэффициенты детерминации
R2скорр.
• Статистическая значимость всех параметров при независимых
переменных
• Значимость всей функции в целом
• Выполнение требований Гаусса-Маркова, предъявляемых к
случайным остаткам модели, в первую очередь, постоянство
дисперсии и независимость друг от друга
41. Использование фиктивных переменных в моделях регрессии
Фиктивная (структурная) переменная – этопеременная, принимающая значение 1 или 0.
Используется при решении следующих задач:
– при моделировании качественных признаков
– для учета структурной неоднородности, к которой
приводят качественные признаки
– для оценки сезонных колебаний
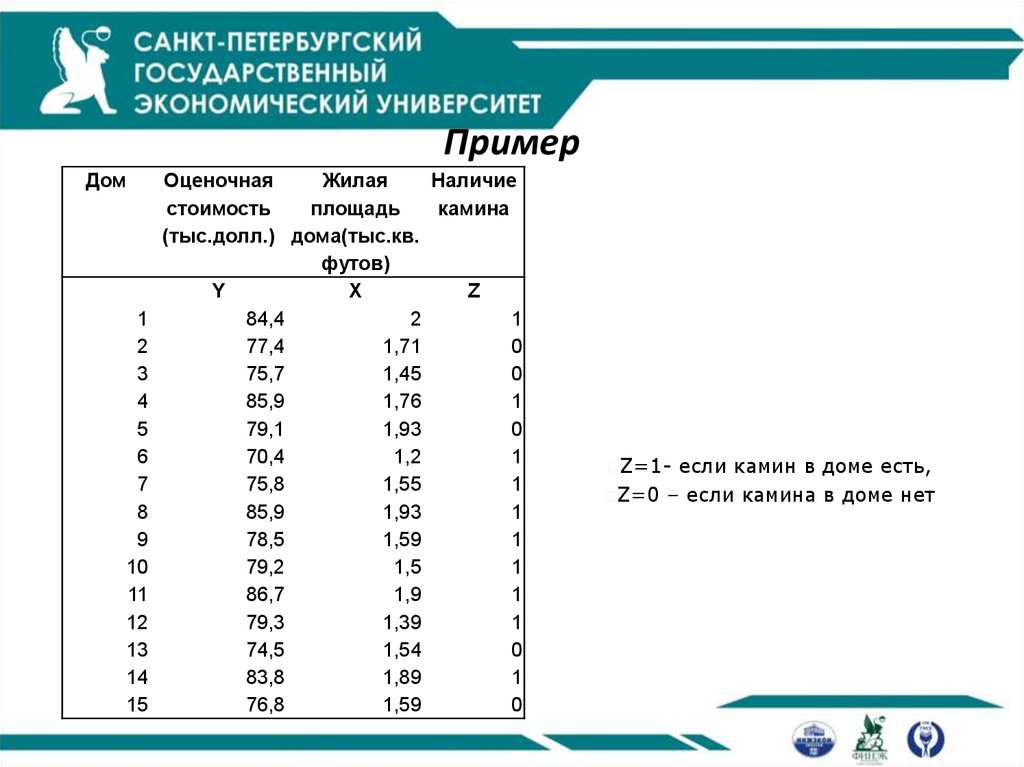
42. Пример
• y – оценочная стоимость жилья• x – жилая площадь
• z – наличие камина
(1- есть камин, 0 – нет камина)
43. Пример
Дом1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Оценочная
Жилая
Наличие
стоимость
площадь
камина
(тыс.долл.) дома(тыс.кв.
футов)
Y
X
Z
84,4
2
1
77,4
1,71
0
75,7
1,45
0
85,9
1,76
1
79,1
1,93
0
70,4
1,2
1
75,8
1,55
1
85,9
1,93
1
78,5
1,59
1
79,2
1,5
1
86,7
1,9
1
79,3
1,39
1
74,5
1,54
0
83,8
1,89
1
76,8
1,59
0
Z=1-
если камин в доме есть,
Z=0 – если камина в доме нет
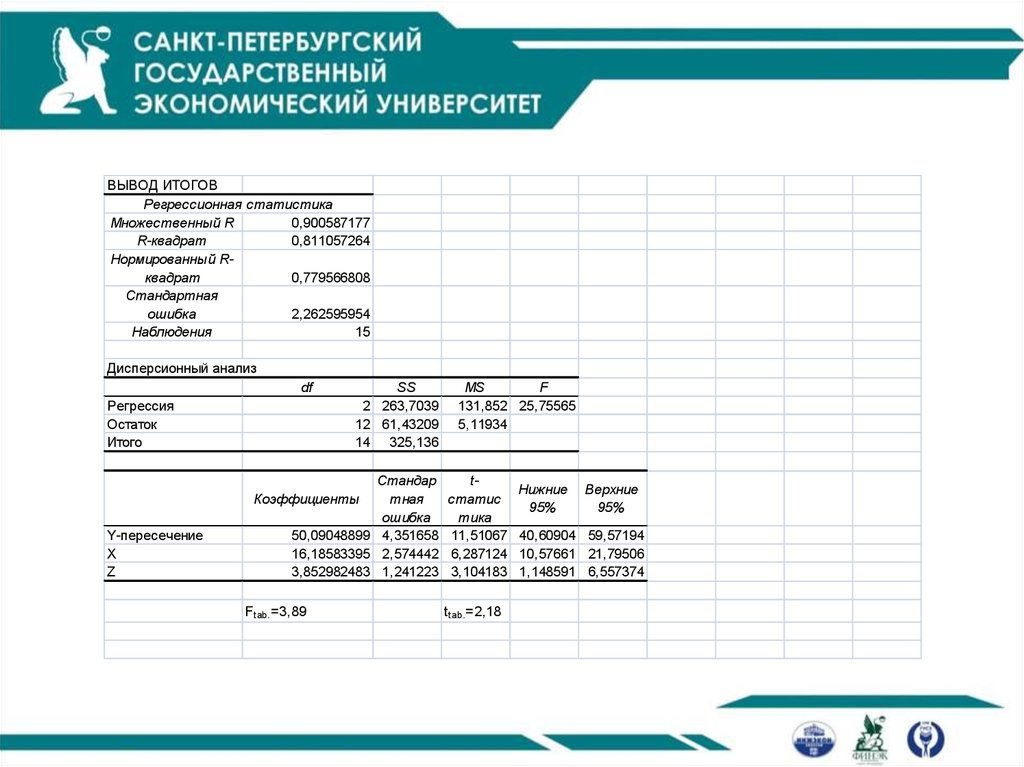
44.
ВЫВОД ИТОГОВРегрессионная статистика
Множественный R
0,900587177
R-квадрат
0,811057264
Нормированный Rквадрат
0,779566808
Стандартная
ошибка
2,262595954
Наблюдения
15
Дисперсионный анализ
df
Регрессия
Остаток
Итого
SS
2 263,7039
12 61,43209
14 325,136
Стандар
тная
ошибка
50,09048899 4,351658
16,18583395 2,574442
3,852982483 1,241223
Коэффициенты
Y-пересечение
X
Z
Ftab. =3,89
MS
F
131,852 25,75565
5,11934
tстатис
тика
11,51067
6,287124
3,104183
t tab. =2,18
Нижние
95%
Верхние
95%
40,60904 59,57194
10,57661 21,79506
1,148591 6,557374
45.
Общий вид уравнения:Yˆ 50,09 16,186 X 3,853Z
Для домов, не имеющих камина:
Yˆ 50,09 16,186 X , поскольку Z=0
Для домов, имеющих камин:
Yˆ 53,943 16,186 X , поскольку Z=1
46.
Интерпретация коэффициентов регрессии в данной модели:1. Увеличение жилой площади на 1000 кв.футов приводит к
увеличению предсказанной средней оценочной стоимости на
16,186 тыс.долл. при условии, что фиктивная переменная
(наличие камина) имеет постоянное значение.
2. Если жилая площадь постоянна, наличие камина увеличивает
среднюю оценочную стоимость дома на 3,853 тыс.долл.
47. Фиктивные переменные в нелинейных моделях (на примере степенной функции)
yx
lny
lnx
ln y ln a b1 ln x b2 z
ln y 4,175 0,335 ln x 0,05 z
yˆ e 4,175 x 0,335e0, 05 z
e 4,175 65
e0, 05 1,05
z
48. Проблемы, возникающие при построении регрессионных моделей
• Мультиколлинеарность• Гетероскедастичность
49. Симптомы мультиколлинеарности
Завышенное значение коэффициента детерминации
Высокие стандартные ошибки для коэффициентов
регрессии
Широкие доверительные интервалы
Низкое значение t-критерия
Появление при коэффициентах регрессии знаков,
противоположных ожидаемым
50. Выявление мультиколлинеарности с помощью матрицы парных коэффициентов корреляции
• Наличие мультиколлинеарности можно подтвердить, найдяопределитель матрицы. Если связь между независимыми
переменными полностью отсутствует, то недиагональные элементы
будут равны нулю, а определитель матрицы - единице.
• Если связь между независимыми переменными близка к
функциональной (то есть является очень тесной), то определитель
матрицы будет близок к нулю.
rx1x1
rx2 x1
...
rx x
p1
rx1x2
rx2 x2
...
rx p x2
... rx1x p
... rx2 x p
... ...
rx p x p
51. Меры по устранению мультиколлинеарности
Удаление из модели переменных с высоким коэффициентом парной
корреляции между факторами, если это не противоречит теории,
положенной в основу построения модели
Увеличение числа наблюдений
Изменение функциональной формы модели
Функциональные преобразования тесно связанных между собой
переменных. Например, поступление налогов в городах зависит от
количества жителей и площади города. Очевидно, что эти переменные
будут тесно связаны. Их можно заменить одной относительной
переменной «плотность населения»
Построение моделей по отклонениям от средней величины
Использование специальных методов обработки временных рядов
52. Гетероскедастичность
Основные предпосылки МНК:– случайный характер остатков
– нулевая средняя остатков, не зависящая от фактора x
– гомоскедастичность (дисперсия каждого отклонения
одинакова для всех значений x)
– отсутствие автокорреляции остатков
– остатки должны подчиняться нормальному
распределению
53. Зависимость остатков от выровненного значения результата
ε 105
нет зависимости (гомоскедастичность)
0
0
5
10
15
20 ŷ
-5
-10
ε 10
5
0
0
-5
-10
5
10
15
20 ŷ
дисперсия остатков увеличивается с
увеличением выровненного значения
результата (один из случаев
гетероскедастичности
54. Меры по устранению гетероскедастичности
• Увеличение числа наблюдений• Изменение функциональной формы модели
• Разделение исходной совокупности на
качественно-однородные группы и проведение
анализа в каждой группе
• Использование фиктивных переменных,
учитывающих неоднородность
• Исключение из совокупности единиц, дающих
неоднородность
55. Тесты, используемые для выявления гетероскедастичности
• Гольдфельда-Квандта• Парка
• Глейзера
• Уайта
56. Тест Гольдфельда-Квандта
• Все наблюдения упорядочивают по мере возрастания какого-либофактора, который, как предполагается, оказывает влияние на
возрастание дисперсии остатков
• Упорядоченную совокупность делят на три группы, причем первая и
последняя должны быть равного объема с числом единиц, больших,
чем число параметров модели регрессии. Число отобранных единиц
обозначим k
По первой и третьей группе находят параметры уравнений регрессии
и остатки по ним
• Используя данные об остатках моделей первой и третьей группы,
рассчитывают фактическое значение F-критерия
57. Тест Гольдфельда-Квандта
SS E 3F
SS E 1
df1=df2=k-m-1
58. Тест Парка
ln e a b ln x v2
59. Тест Глейзера
e a bx vk
• k – какое-либо число, например, k= – 1; – 0,5; 0,5; 1
60. Тест Уайта
e a bx cx v2
2

















































 mathematics
mathematics








