Множественная регрессия в эконометрических расчетах

1. МНОЖЕСТВЕННАЯ

РЕГРЕССИЯ
в эконометрических расчетах

2. ВАЖНОСТЬ ИСПОЛЬЗОВАНИЯ

При использовании парной регрессии
предполагается, что влиянием других
факторов на результат можно пренебречь
(сделать их неизменными)
В реальной практике экономические данные
зафиксировать не удается и чистое влияние
двух переменных друг на друга выделить
нельзя, поэтому используется множественная
регрессия, дополнительные факторы вводят
в модель

3. СФЕРА ПРИМЕНЕНИЯ

Решение задач оценки
объема спроса,
доходности акций
плановых издержек
макроэкономических прогнозов

4. Цель применения

Построить модель с большим числом
факторов, определив при этом влияние
каждого из них в отдельности на
результат, а также совокупное
воздействие их на моделируемый
показатель

5. Основные предпосылки модели множественной регрессии

Математическое ожидание всех εi равно
нулю для всех наблюдений;
Дисперсии всех εi постоянны и равны;
εi – независимы друг от друга и от х1…хр;
εi – имеют распределение Гаусса N(0;σ²);
Модель линейна относительно
параметров ß1 … ßр;
Между х1…хр отсутствует строгая
линейная связь (нет
мультиколлинеарности факторов);

6.

7.

8.

9.

10. Остатки случайны

11. Графический анализ остатков

Остатки не являются случайными
величинами

12. Графический анализ остатков

Остатки не являются случайными
величинами

13. НУЖНО

Применить другую функцию
или
Добавить информации , пока остатки не
станут случайными

14. УРАВНЕНИЕ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ

Yˆ a0 a1 x1 a2 x2 ... a p x p , m p 1
По МНК вектор оценок параметров модели регрессии находится
по формуле:
1
a ( X X ) X Y
Значимость уравнения подтверждается коэффициентом
n
детерминации
( y yˆ )
1
( y y)
n
R
2
i 1
n
i
i
2
i
2
( yˆ
i 1
n
i 1
i
y)
2
( yi y )
2
i 1
Критерий значимости
Фишера, n – число наблюдений, m – число
параметров в модели регрессии (число коэффициентов
регрессии):
R 2 ( n m)
F
F (k1 m 1; k 2 n m)
2
(1 R )( m 1)

15. МАТРИЦЫ Х ,У, А и Е

1 x11 x p1
1 x12 x p 2
X
, поэтому m p 1
1 x x
1n
pn
a0
y1
1
a2
y2
2
Y A E
y
a
n
n
p

16. СКОРРЕКТИРОВАННЫЙ R²

Чтобы получить более объективную оценку
качества уравнения регрессии R²
корректируют на количество наблюдений
и факторов
n 1
2
R 1
(1 R )
n p 1
2
ck

17. Доверительные интервалы для среднего значения Y и индивидуального значения Уi в случае множественной регрессии

Yˆi tтабл (n m) SY i , где SY i S X i ( X T X ) 1 X tT ,
S
2
ˆ
(
y
y
)
i i
n p 1
, S 2 остаточная дисперсия
Yˆi tтабл (n m) SY i , где SY i S 1 X i ( X T X ) 1 X tT

18. МЕТОДЫ ПОСТРОЕНИЯ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ

Метод исключения (отсев фактора из
полного набора)
Метод включения (введение нового
фактора)
Шаговый регрессионный анализ
(исключение введенного ранее
фактора)

19. ОТСЕВ ФАКТОРОВ

1 путь. Проводится по показателям не парной
, а частной корреляции, которые в чистом
виде оценивают взаимосвязь между
фактором и результатом. Строится матрица
частных коэффициентов корреляции
2 путь. По критерию Стьюдента из уравнения
исключаются те факторы, у которых значение
критерия меньше табличного

20. ЧАСТНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Позволяет установить степень «чистого» влияния
факторного признака на результативный признак, при
условии, что остальные факторы не влияют,
изменяется от 0 до 1, не может быть больше по
величине коэффициента множественной корреляции.
ryxk ( x1 , x2 ...xk 1 )
R R
2
k
2
k 1
1 R
2
k
Где R²k – коэффициент множественной детерминации
между у и х1…хк;
R²k-1 – коэффициент множественной детерминации
между у и х1…хк-1;

21. ЧАСТНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Если парный коэффициент корреляции
между х и у больше частного
коэффициента корреляции между х и у,
то существует фактор, усиливающий
влияние х на у, если наоборот, то
существует фактор, ослабляющий это
влияние

22. СПЕЦИФИКАЦИЯ МОДЕЛИ

Отбор факторов
Выбор вида уравнения

23. ОТБОР ФАКТОРОВ

Факторы, включаемые в модель должны
удовлетворять требованиям:
1. Быть количественно измеримы или
задаваться фиктивными переменными
2. Не должны быть коррелированы
между собой (отсутствие
мультиколлинеарности)

24. ОТБОР ФАКТОРОВ

Включаемые в модель факторы должны
объяснять вариацию зависимой переменной
R2 – доля объясненной вариации зависимой
переменной за счет влияния факторов
модели
(1-R2) – остаточная дисперсия S2
При дополнительном включении в регрессию
фактора R2 должен расти, а S2 уменьшаться
Насыщение модели лишними факторами не
снижает S2,но и приводит к статистической
незначимости параметров регрессии

25. ИССЛЕДОВАНИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ

Наличие существенной связи между факторами –
мультиколлинеарности факторов - ведет к ненадежности оценок
уравнения регрессии и прогнозов на их основе.
Для оценки её наличия используют определитель матрицы
парных линейных коэффициентов корреляции между факторами,
например для 3 факторов:
rx1x1
rx 2 x1
rx 3 x1
det R rx1x 2
rx 2 x 2
rx 3 x 2
rx1x 3
rx 2 x 3
rx 3 x 3
Чем ближе значение определителя к нулю, тем сильнее
мультиколлинеарность факторов и ненадежней
результаты множественной регрессии

26. Проверка гипотезы о независимости факторов – отсутствии мультиколлинеарности

H0: Det|R|=1, то есть
мультиколлинеарности нет
H1:Det|R|=0 , то есть она есть
Если χ²расч>χ²(α;0,5(m(m-1)), то H0
отклоняется и мультиколлинеарность
факторов доказана
Χ²расч=[n-1-(1/6)(2m+5)lgDetR]

27. УСТРАНЕНИЕ МУЛЬТИКОЛИНЕАРНОСТИ

Исключение из модели наиболее
мультиколлинеарных факторов (строят
множественную регрессию относительно
каждого фактора и исключают фактор с
максимальным R2)
Преобразование факторов через их
объединение или изменение (Δ)
Совмещенные уравнения регрессии (при
коэффициенте регрессии стоит не один, а
произведение факторов)
Использование уравнений регрессии
приведенной формы

28. РАНЖИРОВАНИЕ ПЕРЕМЕННЫХ Х ПО МЕРЕ ИХ ВЛИЯНИЯ НА У

(если переменные Х имеют разные единицы
измерения )
на основе коэффициентов эластичности:
Эj a j
xj
y
,
j 1.. p
и стандартизированных
s x j коэффициентов
регрессии: a
, j 1.. p
j
j
sy

29. ПРОВЕРКА ЗНАЧИМОСТИ Хj

На основе t-критерия Стьюдента
t
aj
Sa j
t / 2 (n m)
тогда оценка параметра модели при хj отлична от
нуля с вероятностью 1-а
Sa j S
( X
T
X ) 1
jj

30. Измерение системного эффекта на основе уравнения регрессии

В науке принято изучать влияние не
отдельных факторов, а целостные
системы факторов и результатов.
Влияние системы не сводится к
арифметической сумме влияний
каждого фактора в отдельности, так как
возникает «системный эффект» синергия

31. Влияние системного эффекта

p
R
2
j 1
2
j

32. ПРИМЕРЫ

33.

34.

35. ПРИМЕРЫ

36.

37. МОРАЛЬ

38.

39. ВЫВОД И МОРАЛЬ

40.

41.

42.

43.

44.

45. ВЫВОД И МОРАЛЬ

46. Свойства ξ

47. Показатель ξ

48. ВЫБОР ФОРМЫ УРАВНЕНИЯ

Чаще всего используются линейная и
степенная функция
Чем сложнее функция, тем больше
нужно данных
Использование более сложных
уравнений не позволяет осуществить
экономическую интерпретацию
коэффициентов, это делает их
использование менее привлекательным

49. Смысл коэффициентов линейной модели

В линейной регрессии свободный член
не имеет смысла, коэффициент
регрессии означает как в среднем
измениться у, если хi измениться на
единицу, а другие факторы будут
неизменны

50. Смысл коэффициентов степенной модели

Коэффициенты при х являются
коэффициентами эластичности и
показывают на сколько % измениться у,
если хi измениться на 1% при
неизменных других факторах
Сумма коэффициентов регрессии не
всегда равна 1

51. Гомоскедастичность остатков –предпосылка МНК

Гомоскедастичность остатков –
предпосылка МНК
Для каждого х дисперсия остатков одинакова

52.

53. Гетероскедастичность остатков

-
Гетероскедастичность
остатков
это непостоянство дисперсии
остатков, которое также приводит к
снижению эффективности применения
уравнения регрессии.
Для её выявления используются различные
критерии - критерий Голдфелда-Квандта, тест
ранговой корреляции Спирмена и д.р.

54. Тест ранговой корреляции Спирмена

рассчитывается коэффициент
Спирмена между модулями остатков и
значениями факторов, если
коэффициент Спирмена значим, то
гетероскедастичность остатков
доказана и уравнение регрессии
ненадежно

55.

Тест ранговой корреляции Спирмена

56. ПРИМЕР

57. Тест Голдфелда-Квандта

58.

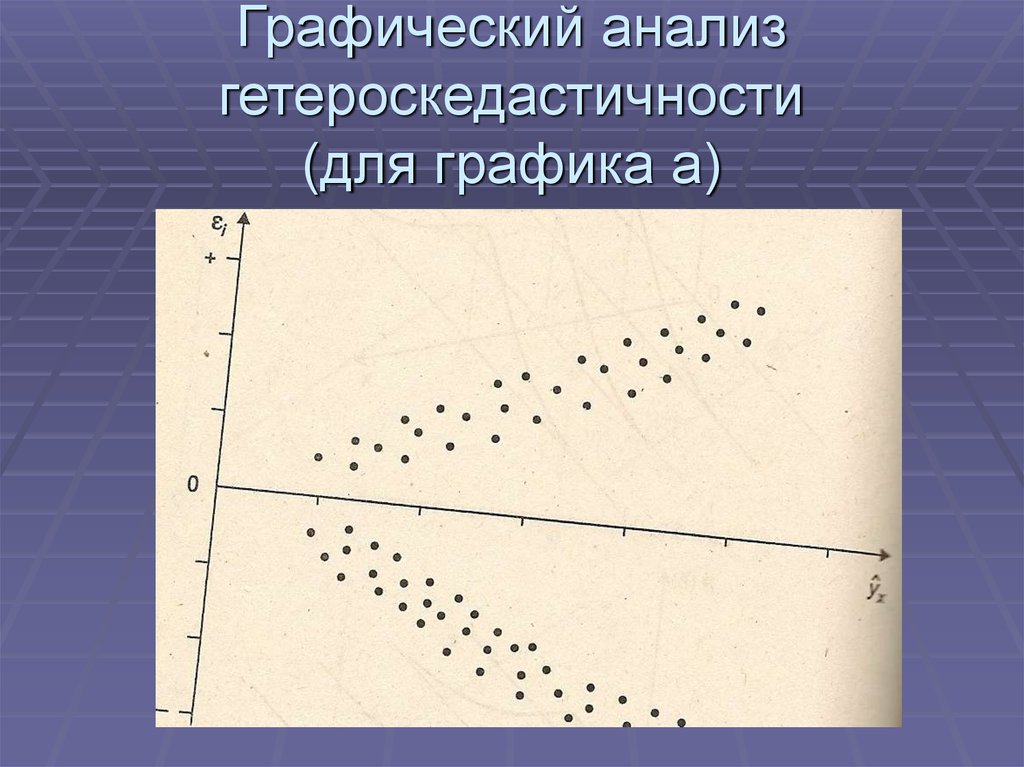
59. Графический анализ гетероскедастичности

а – дисперсия остатков растет при росте х
б – дисперсия остатков при минимальном и
максимальном значении х минимальна, при среднем
значении х - максимальна

60. Графический анализ гетероскедастичности (для графика а)

61. Графический анализ гетероскедастичности (для графика б)

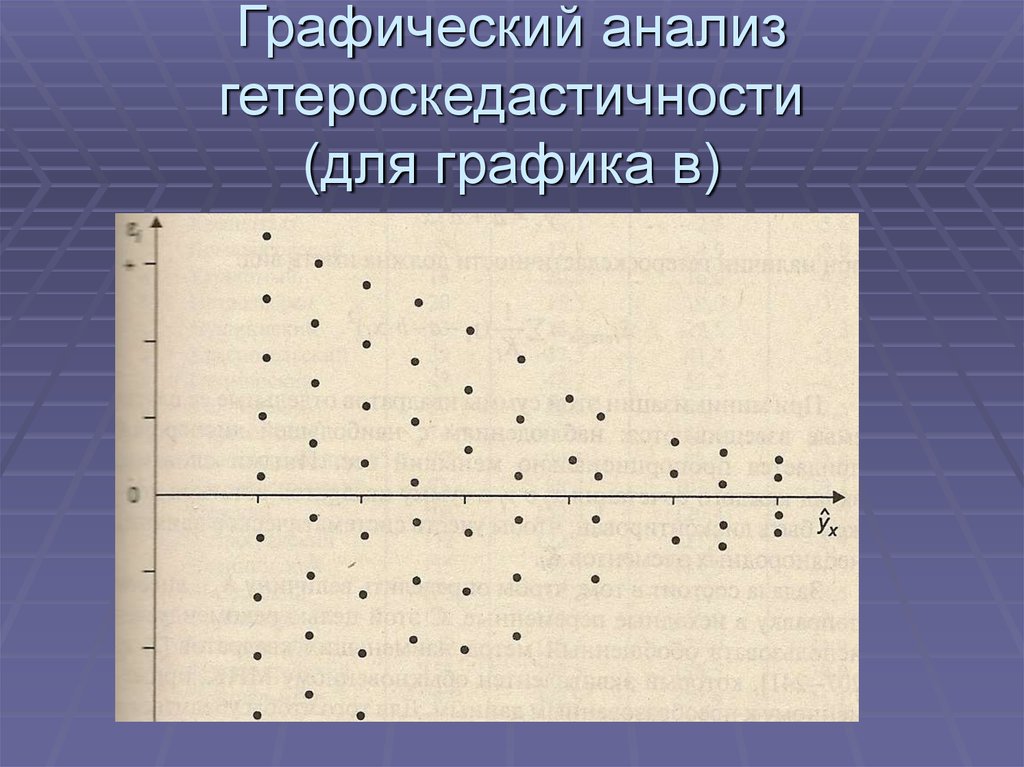
62. Графический анализ гетероскедастичности

в – дисперсия остатков максимальна при
минимальных значениях х

63. Графический анализ гетероскедастичности (для графика в)

64. Автокорреляция остатков

Для надежности результатов регрессии
необходимо, чтобы автокорреляции
остатков не было.
Её проверяют, например, на основе
коэффициента автокорреляции ra
n
i i 1
ra
2
n
2
i
, если ra меньше табличного,
1
то автокорреляции остатков нет

65.

66. Пример использования DW

67. УСЛОВИЯ ИСПОЛЬЗОВАНИЯ УРАВНЕНИЙ РЕГРЕССИИ ДЛЯ ПРОГНОЗА

Если совокупность неоднородна по
исследуемым признакам, то уравнение
регрессии не имеет смысла
Должны быть неизменны условия
формирования уровней признаков,
которые лежат в основе определения
оценок параметров модели регрессии.
Иначе необходимо собирать новый
эмпирический материал, отражающий
взаимосвязь признаков в новых
условиях.

68. ПРИЗНАКИ ХОРОШЕЙ МОДЕЛИ

Модель должна быть простой;
Для любого набора статистических данных
определяемые коэффициенты уравнения
модели должны определяться однозначно;
Стремятся строить модели с максимально
возможным скорректированным
коэффициентом детерминации R²;
Модель не может быть признана
качественной, если она не соответствует
известным теоретическим предпосылкам;
Модель признается качественной, если
полученные на её основе прогнозы
подтверждаются реальностью.

69. ОШИБКИ СПЕЦИФИКАЦИИ

- это неправильный выбор
функциональной формы модели или
набора объясняющих переменных
х1…хр
Основные их виды:
Игнорирование значимой переменной
(не включение её в модель);
Добавление в модель незначимой
переменной;
Выбор неправильной функциональной
формы.

70. Любая качественная модель – подгонка спецификации модели под имеющиеся данные

Из-за меняющихся условий
протекания экономических процессов
необходим постоянный пересмотр
модели;
При всех недостатках моделей
принятие решений на их основе
приводит к более точным
результатам, чем принятие решений
на основе интуиции и законов
экономической теории