Similar presentations:
Эконометрическое моделирование рождаемости в Оренбургской области
1. Индивидуальное задание по дисциплине «Эконометрика» Эконометрическое моделирование рождаемости в Оренбургской области
Руководители работы:канд. технических
наук, доцент
А.Г. Реннер
канд. экономических
наук, доцент
О.С. Чудинова
Исполнитель:
студент гр. 11ПМ(б)ОП
Л. В. Зверева
2. Цель, предмет и объект исследования
Цель исследования - выявление социальнодемографических факторов и количественнаяоценка их влияния на рождаемость в регионе.
Предмет исследования - эконометрические
модели, описывающие влияние социальнодемографических факторов на рождаемость в
регионе.
Объект исследования - муниципальные
образования Оренбургской области.
2
3. Задачи исследования
• исходя из экономических соображений, отобратьсоциально-демографические факторы, влияющие на
рождаемость;
• провести регрессионный анализ рождаемости на основе
линейной модели множественной регрессии;
• проверить соответствие линейной модели множественной
регрессии условиям Гаусса-Маркова;
• исследовать выборочную совокупность на регрессионную
однородность;
• провести регрессионный анализ рождаемости на основе
нелинейных моделей;
• осуществить сценарное прогнозирование рождаемости.
3
4. Набор показателей
К выбранным показателям относятся:y - число родившихся (чел)
x1 - число браков
x2 - заболеваемость на 1000 человек населения (чел)
x3 - численность безработных, зарегистрированных в
государственных учреждениях службы занятости
населения (чел)
x4 - численность женщин (чел)
x5 - средний возраст (лет)
4
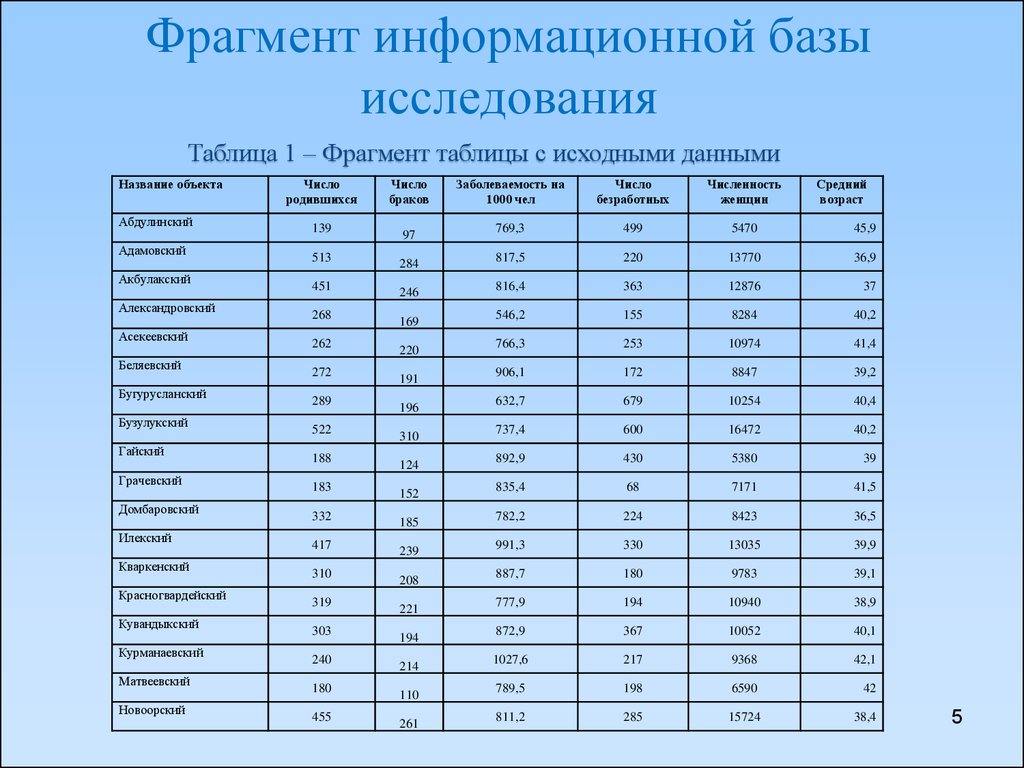
5. Фрагмент информационной базы исследования
Таблица 1 – Фрагмент таблицы с исходными даннымиНазвание объекта
Абдулинский
Адамовский
Акбулакский
Александровский
Асекеевский
Беляевский
Бугурусланский
Бузулукский
Гайский
Грачевский
Домбаровский
Илекский
Кваркенский
Красногвардейский
Кувандыкский
Курманаевский
Матвеевский
Новоорский
Число
родившихся
139
513
451
268
262
272
289
522
188
183
332
417
310
319
303
240
180
455
Число
браков
97
284
246
169
220
191
196
310
124
152
185
239
208
221
194
214
110
261
Заболеваемость на
1000 чел
Число
безработных
Численность
женщин
Средний
возраст
769,3
499
5470
45,9
817,5
220
13770
36,9
816,4
363
12876
37
546,2
155
8284
40,2
766,3
253
10974
41,4
906,1
172
8847
39,2
632,7
679
10254
40,4
737,4
600
16472
40,2
892,9
430
5380
39
835,4
68
7171
41,5
782,2
224
8423
36,5
991,3
330
13035
39,9
887,7
180
9783
39,1
777,9
194
10940
38,9
872,9
367
10052
40,1
1027,6
217
9368
42,1
789,5
198
6590
42
811,2
285
15724
38,4
5
6. Классическая линейная модель множественной регрессии
~y 0 1 x1 2 x2 3 x3 ... k xk
(1)
yi 0 1 xi1 2 xi 2 3 xi 3 ... k xik zi , i 1..n
(2)
Y X z
(3)
y1
y
Y 2
y
n
x11
x
X 21
...
xn1
x12
x22
...
xn 2
... x1k
... x2 k
... ...
... xnk
zi yi ~
yi , i 1..n
1,n = Xβ +
n 41
k 5
(4)
Условия Гаусса-Маркова
1) х1,…,хк – детерминированные (неслучайные) величины
2) ранг матрицы X равен к+1
3) M i 0 i 1, n
4) D i M i2 2
5) cov( i , j ) M ( i j ) 0 i j i 1, n
4') M T 2 En
(5)
j 1, n
6
7. Оценка коэффициентов ЛММР методом наименьших квадратов
n2
z
i min
(6)
i 1
n
G ( 0 ,..., k ) ( yi 0 1 xi1 ... k xik ) 2 (Y X )T (Y X )
(7)
i 1
Y T Y Y T X T X T Y T X T X Y T Y 2 T X T Y T X T X min
X T X X T Y
(8)
ˆ МНК ˆ ( X T X ) 1 X T Y
(9)
yˆ 696.76 0.88 x1 0.13x2 0.01x3 0.009 x4 13.63x5
(10)
(0.15)
(0.05)
(0.03) (0.003)
(2.94)
Rˆ 2 0.99
7
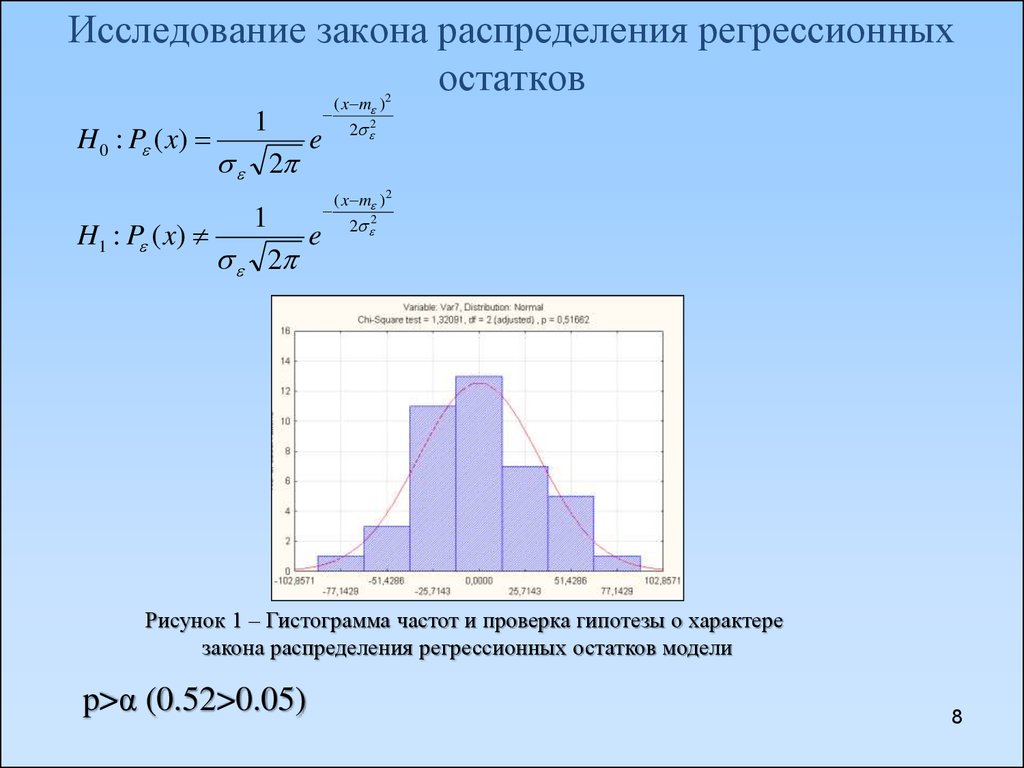
8. Исследование закона распределения регрессионных остатков
( x m )H 0 : P ( x)
H1 : P ( x)
1
2
1
2
e
e
2
2 2
( x m )2
2 2
Рисунок 1 – Гистограмма частот и проверка гипотезы о характере
закона распределения регрессионных остатков модели
p>α (0.52>0.05)
8
9. Проверка выполнения третьего условия Гаусса-Маркова
H 0 : M 0(11)
H1 : M 0
t
t набл
e M
ˆ ост
e M
ˆ ост
n
tкрлев u 2,02
2
n t (n 1)
(12)
0.000006 0
41 0,000001
35.83
t крпр u
1
2,02
2
9
10. Проверка значимости ЛММР
H 0 : 1 2 ... 5 0H 1 : j (1..5) : j 0
Qфакт / k
Rˆ 2 / k
F
F (k , n k 1)
(1 Rˆ 2 ) / n k 1 Qост / n k 1
(13)
(14)
Fнабл 8291,5
Fкр u0,95 2.49
Fнабл Fкр (8291,5 2.49)
10
11. Проверка значимости и построение доверительных интервалов для коэффициентов модели
H 0 : j 0, j 0..kˆ j
t
t (n k 1)
S ˆ
(15)
(16)
j
t0набл 5,16; t1набл 5,81; t2 набл 2,7; t3набл 0,33; t4набл 3,41; t5набл 4,63
tкрлев u 2,03
t крпр u
1
2
2,03
2
ˆ j ( 1,n ) j
t
t (n k 1)
S ˆ ( 1,n )
(17)
j
ˆ j S ˆ j ˆ j S ˆ
j
0.53 1 1.23
(18)
j
0.17 2 0.09
0.002 4 0.02
0.081 3 0.061
20.5 5 6.7
11
12. Исследование линейной модели множественной регрессии на наличие мультиколлинеарности объясняющих переменных
Рисунок 2 - Оценка матрицы парных коэффициентов корреляцииRˆ x21 / x2 , x3 , x4 , x5 0.99
Rˆ x23 / x1 , x2 , x4 , x5 0.69
cond X X
T
max | j |
min | j |
1,686 1012
(19)
Rˆ x24 / x1 , x2 , x3 , x5 0.99
12
13. Устранение мультиколлинеарности между объясняющими переменными линейной модели множественной регрессии
yˆ 683.57 0.9 x1 0.13x2 0.009 x4 13.43x5(127.58) (0.15) (0.05) (0.002)
(2.84)
Rˆ 2 0.99
(20)
( X T X E ) X T Y
(21)
ˆ ( X T X E) 1 X T Y
0.3
yˆ 802.17 0.55 x1 0.13x2 0.54 x3 0.01x4 17.77 x5
(1281.92) (0.12)
(0.48)
(0.26)
(0.002) (25.69)
Rˆ 2 0.88
(22)
yˆ 686.99 0.89 x1 0.13x2 0.01x3 0.009 x4 13.43x5
(134.12) (0.15)
(0.05)
(0.03)
(0.009)
(2.93)
(23)
13
14. Устранение мультиколлинеарности путем перехода к ортогональным переменным
Рисунок 3 - Вклады главных компонент всуммарную дисперсию исходных признаков
Рисунок 4 – Матрица нагрузок
z1 0.58 x1* 0.15 x2* 0.54 x3* 0.58 x4* 0.15 x5*
(24)
z2 0.01x1* 0.761x2* 0.027 x3* 0.02 x4* 0.65 x5*
yˆ 622.1 1123.4 f1
Rˆ 2 0.95
(41.78) (42.3)
yˆ 2380.38 0.479 x1 0.819 x2 1.227 x3 0.008x4 48.049 x5
(25)
(26)
14
15. Обобщенная линейная модель множественной регрессии
Y X z(27)
1,n = Xβ +
1) х1,…,хк – детерминированные переменные
2) ранг матрицы X равен к+1
3) M i 0 i 1, n
4)
D i M i2 i
2
5) cov( i , j ) M ( i j ) 0 i j i 1, n
4') M T 02 0
(28)
i 1, n
j 1, n
( 0 En )
15
16. Обобщенный метод наименьших квадратов
0 СС T(29)
1,n = Xβ +
(30)
C 1 1,n = C 1 Xβ + C 1
1, n пр
= X пр β + пр
ˆОМНК = (X T 0 1 X) 1 X T 0 1Y
Sˆ02
1
(Y X )T 0 1 (Y X )
n k 1
ˆ
ОМНК
(31)
(32)
(33)
(34)
Sˆ02 (X T 0 1 X) 1
16
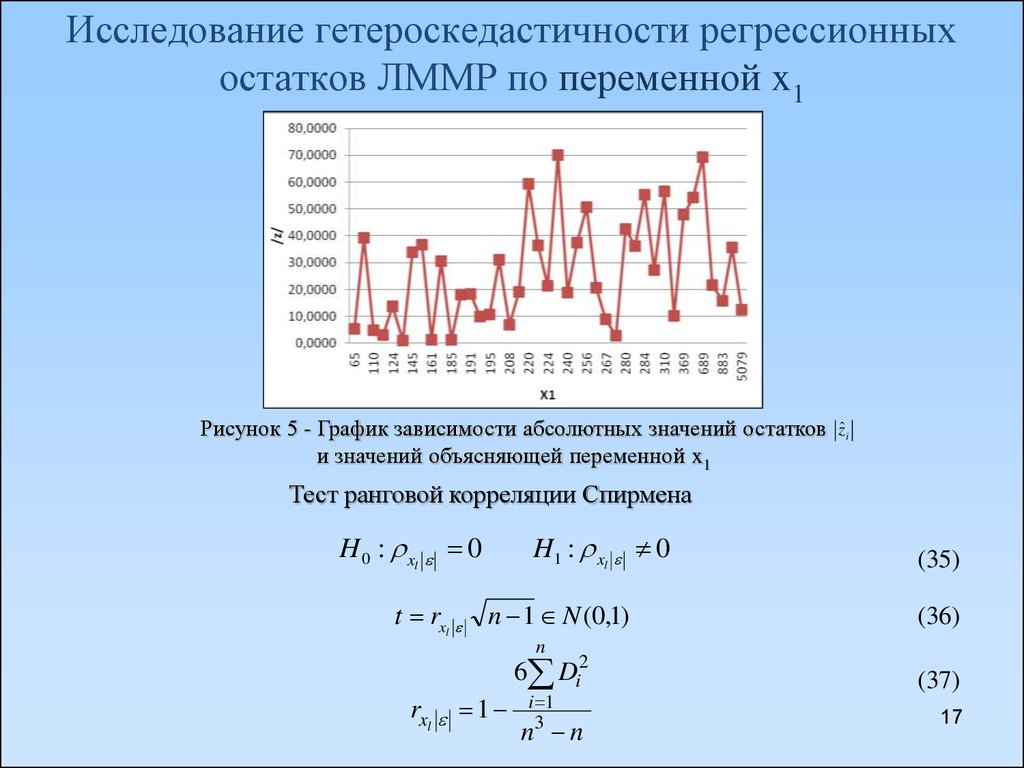
17. Исследование гетероскедастичности регрессионных остатков ЛММР по переменной x1
Рисунок 5 - График зависимости абсолютных значений остаткови значений объясняющей переменной x1
zˆ i
Тест ранговой корреляции Спирмена
H 0 : xl 0
t rxl
H1 : xl 0
n 1 N (0,1)
(35)
(36)
n
rxl 1
6 Di2
i 1
3
n n
(37)
17
18. Исследование гетероскедастичности регрессионных остатков ЛММР по переменной x1
rx1 z 0,41Рисунок 6 - Результат расчета рангового
коэффициента корреляции Спирмена
p<α (0.008<0.05)
Тест Голдфелда-Квандта
H 0 : 12 22 n2
H 1 : i, j :
2
i
(38)
2
j
max {Q1 ; Q2 } /( n ' k 1)
F
F (n ' k 1, n k 1)
min{ Q1 ; Q2 } /( n k 1)
Q 17340
41 0.25 41
Fкрит 2.4
F
4,5
n n
15
набл
Q 3852,91
2
(39)
Тест Глейзера
zˆi xil i
(40)
Таблица 2 - Результаты оценивания регрессионной модели
zˆi 37,47 3694,9 | xi1 | 1.1
(41)
(1603, 4 )
18
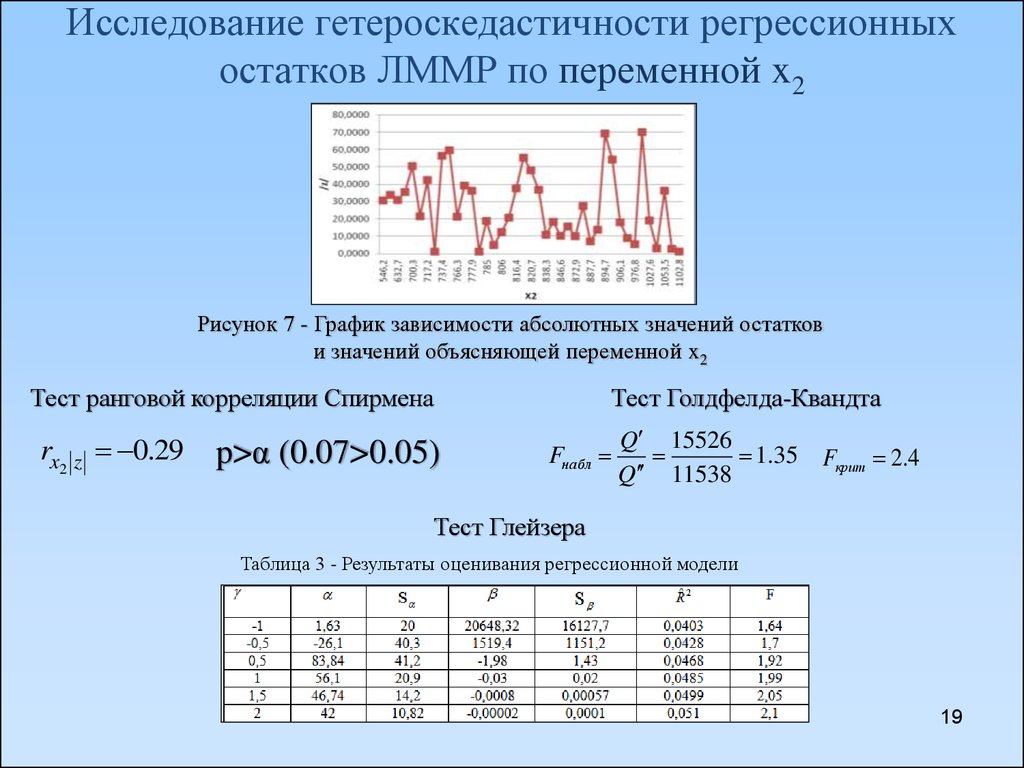
19. Исследование гетероскедастичности регрессионных остатков ЛММР по переменной x2
Рисунок 7 - График зависимости абсолютных значений остаткови значений объясняющей переменной x2
Тест ранговой корреляции Спирмена
rx2 z 0.29
p>α (0.07>0.05)
Тест Голдфелда-Квандта
Fнабл
Q 15526
1.35
Q 11538
Fкрит 2.4
Тест Глейзера
Таблица 3 - Результаты оценивания регрессионной модели
19
20. Исследование гетероскедастичности регрессионных остатков ЛММР по переменной x4
Рисунок 8 - График зависимости абсолютных значений остаткови значений объясняющей переменной x4
Тест ранговой корреляции Спирмена
rx2 z 0.42
Тест Голдфелда-Квандта
Fнабл
p<α (0.006<0.05)
Q 16237
4,2
Q 3875.51
Fкрит 2.4
Тест Глейзера
Таблица 4 - Результаты оценивания регрессионной модели
zˆi 38.5 49319.3 | xi1 | 0.9
( 21121, 67)
(42)
20
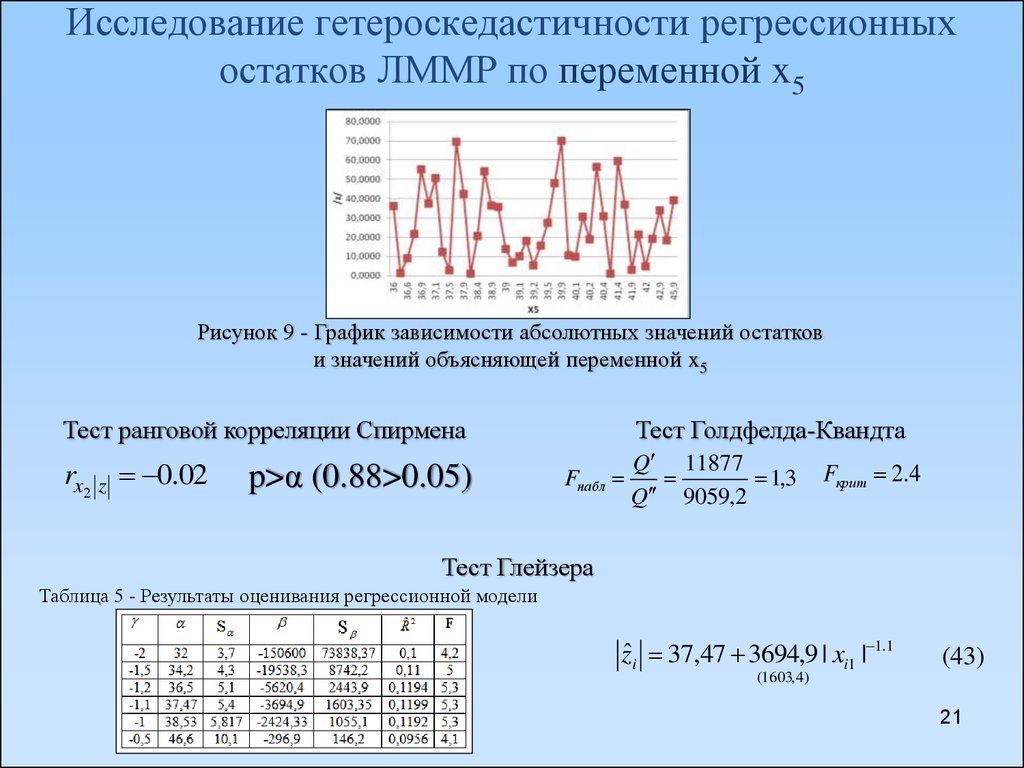
21. Исследование гетероскедастичности регрессионных остатков ЛММР по переменной x5
Рисунок 9 - График зависимости абсолютных значений остаткови значений объясняющей переменной x5
Тест ранговой корреляции Спирмена
rx2 z 0.02
p>α (0.88>0.05)
Тест Голдфелда-Квандта
Fнабл
Q 11877
1,3
Q 9059,2
Fкрит 2.4
Тест Глейзера
Таблица 5 - Результаты оценивания регрессионной модели
zˆi 37,47 3694,9 | xi1 | 1.1
(43)
(1603, 4 )
21
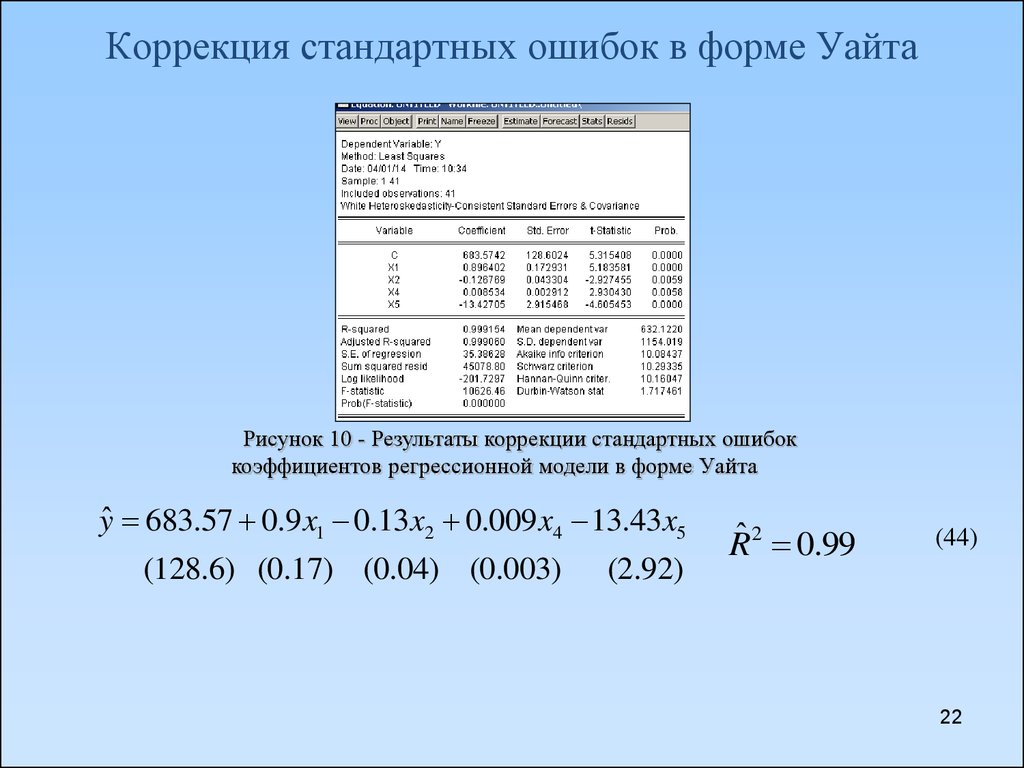
22. Коррекция стандартных ошибок в форме Уайта
Рисунок 10 - Результаты коррекции стандартных ошибоккоэффициентов регрессионной модели в форме Уайта
yˆ 683.57 0.9 x1 0.13x2 0.009 x4 13.43x5
(128.6) (0.17) (0.04) (0.003)
(2.92)
Rˆ 2 0.99
(44)
22
23. Исследование линейной модели множественной регрессии на наличие автокорреляции регрессионных остатков
H 0 : ( i , i 1 ) 0(45)
H1 : ( i , i 1 ) 0
Статистика Дарбина-Уотсона
n
(ei ei 1 ) 2
DW i 2
(46)
n 1
ei2
i 1
DWнабл 0, d Н
- принимается гипотеза о наличии положительной автокорреляции
DWнабл 4 d Н ,4
- принимается гипотеза о наличии отрицательной автокорреляции
DW набл d В ,4 d В - принимается гипотеза об отсутствии автокорреляции
DWнабл d Н , d В 4 d В ,4 d Н - область неопределенности критерия
Н1
0
Н0
dн
dв
Н0
2
Н1
4 dв
4 dн
4
23
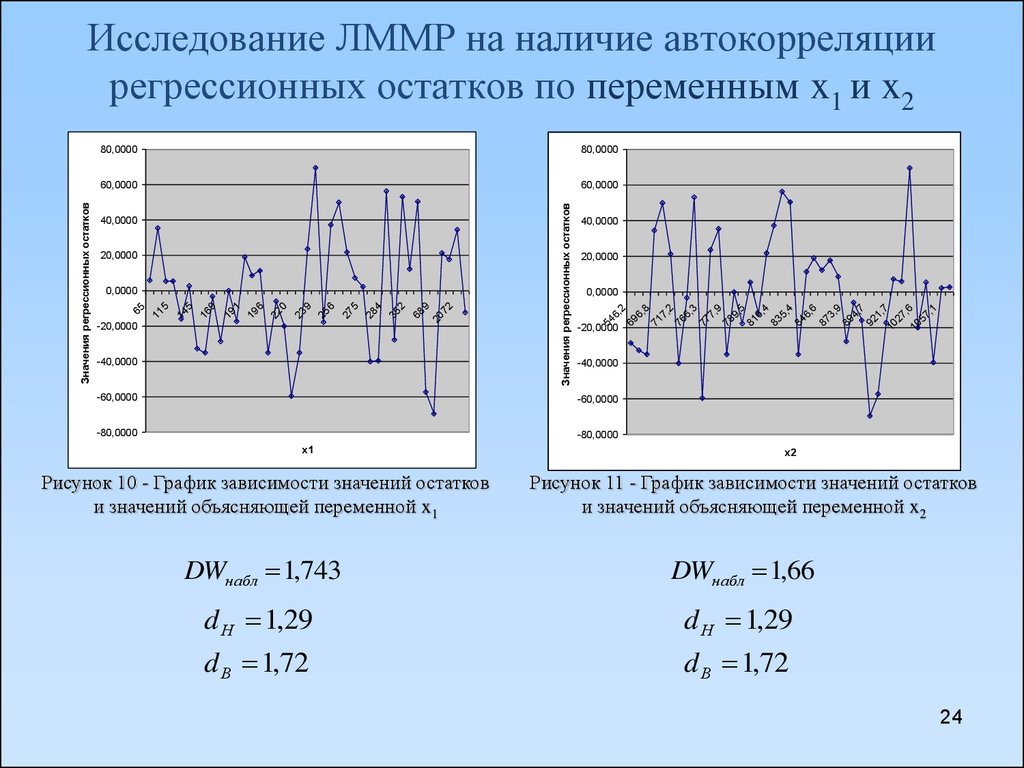
24. Исследование ЛММР на наличие автокорреляции регрессионных остатков по переменным x1 и x2
80,000060,0000
60,0000
20,0000
35
2
68
9
20
72
-20,0000
28
4
27
5
25
6
23
9
22
0
19
6
19
1
16
9
14
5
0,0000
-40,0000
-60,0000
40,0000
20,0000
0,0000
54
6,
2
69
6,
8
71
7,
2
76
6,
3
77
7,
9
78
9,
5
81
6,
4
83
5,
4
84
6,
6
87
3,
9
89
4,
7
92
1,
7
10
27
,
10 6
57
,1
40,0000
Значения регрессионных остатков
80,0000
65
11
5
Значения регрессионных остатков
Исследование ЛММР на наличие автокорреляции
регрессионных остатков по переменным x1 и x2
-20,0000
-40,0000
-60,0000
-80,0000
-80,0000
x1
Рисунок 10 - График зависимости значений остатков
и значений объясняющей переменной x1
x2
Рисунок 11 - График зависимости значений остатков
и значений объясняющей переменной x2
DWнабл 1,743
DWнабл 1,66
d Н 1,29
d Н 1,29
d В 1,72
d В 1,72
24
25. Исследование ЛММР на наличие автокорреляции регрессионных остатков по переменным x4 и x5
80,000060,0000
60,0000
0,0000
-20,0000
-40,0000
-60,0000
20,0000
0,0000
-20,0000
42
43
,3
20,0000
40,0000
36
36
,9
37
,1
37
,9
38
,4
38
,9
39
,1
39
,3
39
,9
40
,2
40
,4
41
,5
40,0000
Значения регрессионных остатков
80,0000
26
06
65
90
74
77
82
84
93
68
10
05
2
10
47
4
12
87
6
13
14
2
15
20
7
15
60
9
19
43
2
38
62
13 5
25
31
Значения регрессионных остатков
Исследование ЛММР на наличие автокорреляции
регрессионных остатков по переменным x4 и x5
-40,0000
-60,0000
-80,0000
-80,0000
x4
Рисунок 12 - График зависимости значений остатков
и значений объясняющей переменной x4
x5
Рисунок 13 - График зависимости значений остатков
и значений объясняющей переменной x5
DWнабл 1,73
DWнабл 1,57
d Н 1,29
d Н 1,29
d В 1,72
d В 1,72
25
26. Построение точечной оценки прогнозируемого значения функции регрессии в точке
yˆ ( X ( n 1) ) X ( n 1) ˆМНК683.57
0
.
9
0.13
0.009
13.43
ˆ МНК
(47)
Таблица 6 - Результаты оценивания прогнозируемого значения регрессии в точке X ( n 1)
Номер сценария
1
T
X ( n 1)
1
65
1103
2606
45.9
yˆ ( X ( n 1) )
6
2
1
424
834
23964
39.5
642
3
1
5079
546
298644
36
7388
26
27. Построение доверительных интервалов для прогнозируемого значения и значения функции регрессии в точке
u ( 1,n )yˆ ( 1,n ) y n 1
t (n k 1)
ˆ пр
(48)
yˆ ( X ( n 1) ) u1 ˆ пр ( X ( n 1) ) y n 1 yˆ ( X ( n 1) ) u1 ˆ пр ( X ( n 1) )
2
(49)
2
(50)
ˆ пр ( X ( n 1) ) ˆ 2 ( X ( n 1) ( X T X ) 1 X ( n 1) 1)
T
Таблица 7 – Доверительные интервалы для прогнозируемого значения
Номер сценария
ˆ пр ( X ( n 1) )
1
2
3
42,83
35,81
49,98
y n 1 y ( X ( n 1) )
Доверительный
интервал
81.166 y n 1 92.560
569.308 y n 1 714.574
7386.640 y n 1 7489.357
X ( n 1) ˆ МНК u1 ˆ fˆ ( X ( n 1) ) f ( X ( n 1) ) X ( n 1) ˆ МНК u1 ˆ fˆ ( X ( n 1) )
2
(51)
2
ˆ fˆ ( X ( n 1) ) ˆ 2 X ( n 1) ( X T X ) 1 X ( n 1)
T
Таблица 8 – Доверительные интервалы для прогнозируемого значения функции регрессии
Номер сценария
1
2
3
ˆ fˆ ( X ( n 1) )
24,13
5,53
35,3
(52)
f ( X ( n 1) )
Доверительный интервал
43.25 f ( X ( n 1) ) 54.64
630.73 f ( X ( n 1) ) 653.15
7316.42 f ( X ( n 1) ) 7459.58
27
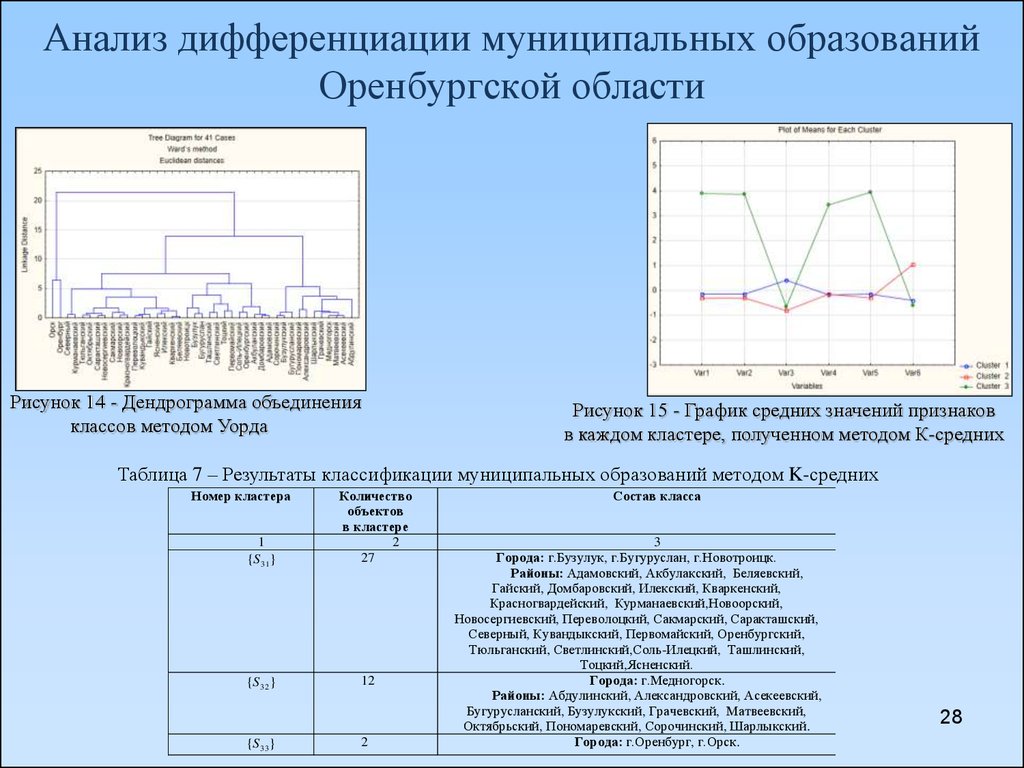
28. Анализ дифференциации муниципальных образований Оренбургской области
Рисунок 14 - Дендрограмма объединенияклассов методом Уорда
Рисунок 15 - График средних значений признаков
в каждом кластере, полученном методом К-средних
Таблица 7 – Результаты классификации муниципальных образований методом K-средних
Номер кластера
1
{S 31}
{S 32 }
{S 33 }
Количество
объектов
в кластере
2
27
12
2
Состав класса
3
Города: г.Бузулук, г.Бугуруслан, г.Новотроицк.
Районы: Адамовский, Акбулакский, Беляевский,
Гайский, Домбаровский, Илекский, Кваркенский,
Красногвардейский, Курманаевский,Новоорский,
Новосергиевский, Переволоцкий, Сакмарский, Саракташский,
Северный, Кувандыкский, Первомайский, Оренбургский,
Тюльганский, Светлинский,Соль-Илецкий, Ташлинский,
Тоцкий,Ясненский.
Города: г.Медногорск.
Районы: Абдулинский, Александровский, Асекеевский,
Бугурусланский, Бузулукский, Грачевский, Матвеевский,
Октябрьский, Пономаревский, Сорочинский, Шарлыкский.
Города: г.Оренбург, г.Орск.
28
29. Регрессионный анализ рождаемости на основе модели с переменной структурой
Критерий ЧоуH 0 : (1) ( 2) , 2(1) 2( 2)
(53)
(eT e e(1)T e(1) e( 2)T e( 2) ) /( k 1) H 0
(1)T (1) ( 2)T ( 2)
F (k 1, n1 n2 2k 2)
(e e e e ) /( n1 n2 2k 2)
nn
1 2
набл
e e e
T
(1)T (1)
e / n2 H 0
F (n2 , n1 k 1)
(1)T (1)
e e / n1 k 1
(41988 25830 7750.2) /( 4 1)
1.452
25830 7750.2
27 12 2 * 4 2
набл
(55)
45079 41988 / 2 1545.5 1.25
41988 / 39 4 1 1234.94
крит 3,28
крит 2,46
d1
(54)
1, объект принадлежит первому классу;
0, иначе.
yˆ 534 1,14 x1 0.15 x 2 0.004 x 4 9,71x5 22,41d1i1
(165.8) (0.22) (0.06)
(0.0036) (3.98)
(22.93)
29
30. Подход Бокса-Кокса
yi ( )yi 1
, i 1..n
xij 1
xij ( )
, i 1..n; j 1..k
(56)
yi ( * ) 0 1 xi1 ( * ) ... k xik ( * ) zi , i 1..n
yi ( * ) 0 1 xi1 ... k xik zi , i 1..n
(57)
ˆММП ( X T X ) 1 X T Y ( )
1
n
2
ˆ ММП
(Y ( ) X )T (Y ( ) X )
n
n
n
1
2
T
lY ( y1 ,..., yn ) ln( 2 ) ln 2 (Y ( ) X ) (Y ( ) X ) ( 1) ln yi
2
2
2
i 1
(58)
yn 1 T
y1 1 y2 1
Y ( ) (
,
,...,
)
30
31. Моделирование числа родившихся с использованием подхода Бокса-Кокса
Таблица 9 – Значения функции максимального правдоподобияlY ( y1 ,..., yn )
-1
-0,8
-0.6
-0.4
-0.2
0.2
0.4
0.5
0.6
0.7
0.8
0.9
1
1.2
1.4
-161.427
-157.222
-153.497
-149.912
-146.642
-142.681
-141.733
-141.498
-141.425
-141.533
-141.875
-142.507
-143.488
-146.634
-151.337
~
yi (0.6) 92.04 0.78~
x1 (0.6) 0.15~
x2 (0.6) 0.04 ~
x4 (0.6) 5.46 ~
x5 (0.6) zi
(17.69) (0.17)
(0.06)
(0.01)
(1.13)
yˆ (61.014 0.78 x10.6 0.15 x20.6 0.04 x40.6 5.46 x50.6 )1.667
Rˆ 2 0.99
(59)
(60)
31
32. Выводы
1. Для описания зависимости уровня рождаемости населения от выбранныхфакторов рассмотрена линейная регрессионная модель. Получено значимое уравнение
регрессии, значимое влияние на число родившихся оказывают число браков,
заболеваемость на 1000 человек населения, численность женщин, средний возраст.
Причем при увеличении числа браков и численности женщин число родившихся будет
увеличиваться, а при увеличении заболеваемости на 1000 человек населения и среднего
возраста – уменьшаться, что не противоречит здравому смыслу.
2. Анализ внешних и формальных признаков показал наличие
мультиколлинеарности между объясняющими переменными. Вследствие этого
реализовано несколько методов устранения мультиколлинеарности: метод пошагового
включения, метод главных компонент, метод «ридж-регрессии» и рекуррентный метод
наименьших квадратов. По экономическим и статистическим соображениям
наилучшим было признано уравнение регрессии, построенное методом пошаговой
регрессии.
3. Проверка наличия/отсутствия гетероскедастичности по каждой из
объясняющих переменных показала, что гетероскедастичность наблюдается более, чем
по одной переменной, поэтому стандартные ошибки коэффициентов модели были
уточены с помощью оценок в форме Уайта.
4. С использованием критерия Дарбина-Уотсона была проведена проверка
наличия/отсутствия автокорреляции по каждой из объясняющих переменных, которая
показала ее отсутствие.
32
33. Выводы
3. Осуществлено сценарного прогнозирования числа родившихся. Былирассмотрены 3 сценария, характеризующиеся «наихудшими», средними и
«наилучшими» значениями объясняющих переменных, для каждого из которых были
построены точечные оценки прогнозируемого значения функции регрессии в точке, а
также доверительные интервалы для прогнозируемого значения и значения функции
регрессии в точке.
4. Для выявления «схожих» по социально-экономическим показателям
муниципальных образований методами кластерного анализа была проведена их
классификация по количественным признакам. В результате все города и районы
Оренбургской области были разбиты на три класса. Наиболее благополучная ситуация,
по сравнению с остальными, наблюдается в том классе, куда входят города Оренбург и
Орск. Для ранжирования муниципальных образований области был построен
интегральный показатель. Результаты ранжирования городов и районов Оренбургской
области в целом согласуются с интерпретацией классов.
5. Результаты проверки гипотезы о регрессионной однородности с помощью
критерия Чоу показали, что выборочная совокупность является однородной в
регрессионном смысле.
6. С использованием преобразования Бокса-Кокса была построена нелинейная
зависимость. Для сравнения полученных оценок уравнений регрессии были найдены
модельные значения, различия в которых оказались незначительными. Принимая во
внимание значение остаточной дисперсии, характеризующей качество модели, было
решено отдать предпочтение линейной модели множественной регрессии, на основании
которой и осуществлялся ранее сценарный прогноз.
33

























 mathematics
mathematics economics
economics








