Similar presentations:
Парная нелинейная регрессия
1.
2.
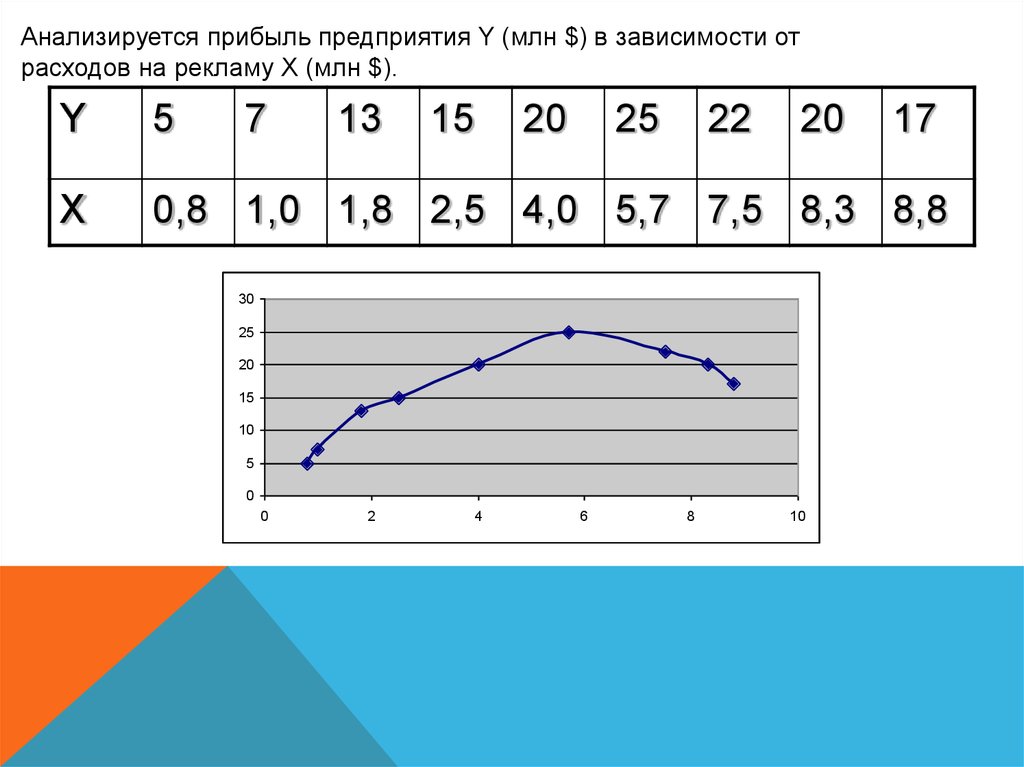
Анализируется прибыль предприятия Y (млн $) в зависимости отрасходов на рекламу X (млн $).
Y
5
7
13
15
20
25
22
20
X
0,8 1,0 1,8 2,5 4,0 5,7 7,5 8,3 8,8
30
25
20
15
10
5
0
0
2
4
6
8
10
17
3.
НЕЛИНЕЙНАЯ МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ1. Регрессии, нелинейные относительно включенных в анализ
объясняющих переменных, но линейные по оцениваемым параметрам
– полиномы различных степеней
y a b1 x b2 x 2 ... bn x n
– равносторонняя гипербола
b
y a
x
– полулогарифмическая функция
y a b ln x
4.
НЕЛИНЕЙНАЯ МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ2. Регрессии, нелинейные по оцениваемым параметрам
– степенная (Лог-модель)
– показательная
– экспоненциальная
y a x
b
y a b
x
y e
a b x
5.
Оценка параметров нелинейной регрессии1. Функции, нелинейные по объясняющим переменным
yˆ x a b1 x b2 x 2
x1 x, x2 x
2
yˆ x a b1 x1 b2 x2
n a b1 x1 b2 x2 y
2
a
x
b
x
1 1 1 b2 x1 x2 x1 y
2
a
x
b
x
x
b
x
2 1 1 2 2 2 x2 y
6.
Оценка параметров нелинейной регрессии1. Функции, нелинейные по объясняющим переменным
b
yˆ x a
x
1
x1
x
yˆ x a b x1
1
n a b x y
a 1 b 1 1 y
x
x
x2
7.
Оценка параметров нелинейной регрессии1. Функции, нелинейные относительно оцениваемых параметров
нелинейные модели
внутренне линейные
нелинейные модели
внутренне нелинейные
логарифмическая модель (степенная):
показательная:
y a x
b
y a bx
экспоненциальная:
y e
a b x
8.
.ПРИМЕР
По статистическим данным, описывающим зависимость значения
рентабельности производства синтетического каучука от индекса
Лернера, построить логарифмическую модель парной регрессии
yˆ a x
Индекс Лернера
Рентабельность, %
b
0,14 0,33 0,21 0,14 0,22 0,25
15,80 49,00 26,20 15,70 27,40 30,00
9.
yˆ a xРЕШЕНИЕ
.
1.
b
ln yˆ ln a b ln x
2. Y ln yˆ , X ln x,1.A244552
ln a
yˆ 179,9383 x
3. Y A b X
yˆ e
Y 5.192614 1.244552 X
5.192614
x
1.244552
10.
Линеаризующие преобразованияМодель
Преобразование
yˆ x a x
yˆ x a b
b Y ln y; X ln x
A ln a
x Y ln y; B ln b
A ln a
Обратная замена
a e b b
A
a e
A
b e
B
11.
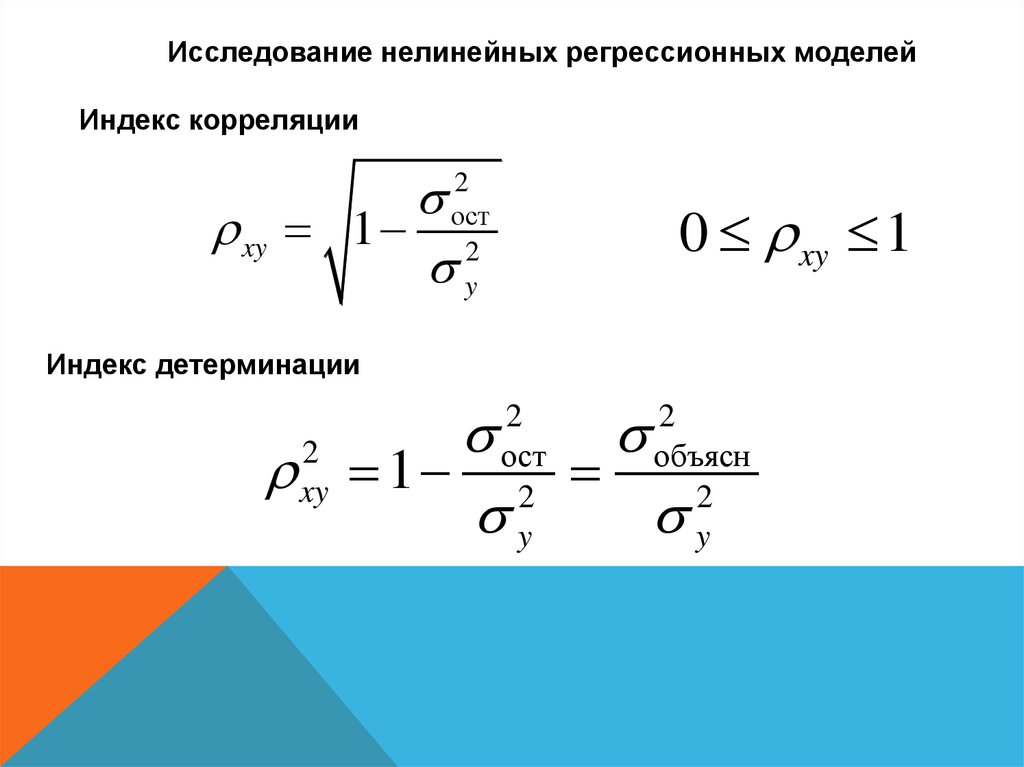
Исследование нелинейных регрессионных моделейИндекс корреляции
xy 1
2
ост
2
y
0 xy 1
Индекс детерминации
1
2
xy
2
ост
2
y
2
объясн
2
y
12.
Исследование нелинейных регрессионных моделей.Критерий Фишера
xy2
n m 1
F
2
1 xy
m
Средняя относительная ошибка аппроксимации
1 n yi yˆ xi
A
100 %
n i 1
yi
13.
Исследование нелинейных регрессионных моделей.x
Э f ( x)
y
Коэффициент эластичности
y a x
b
y a b x
Э b
Средний коэффициент эластичности
b 1
x
Э f x
y
14.
ПРИМЕРy a b ln x
y a b
y a x
b
x
X ln x
X
x
Y ln y; X ln x
A ln a
15.
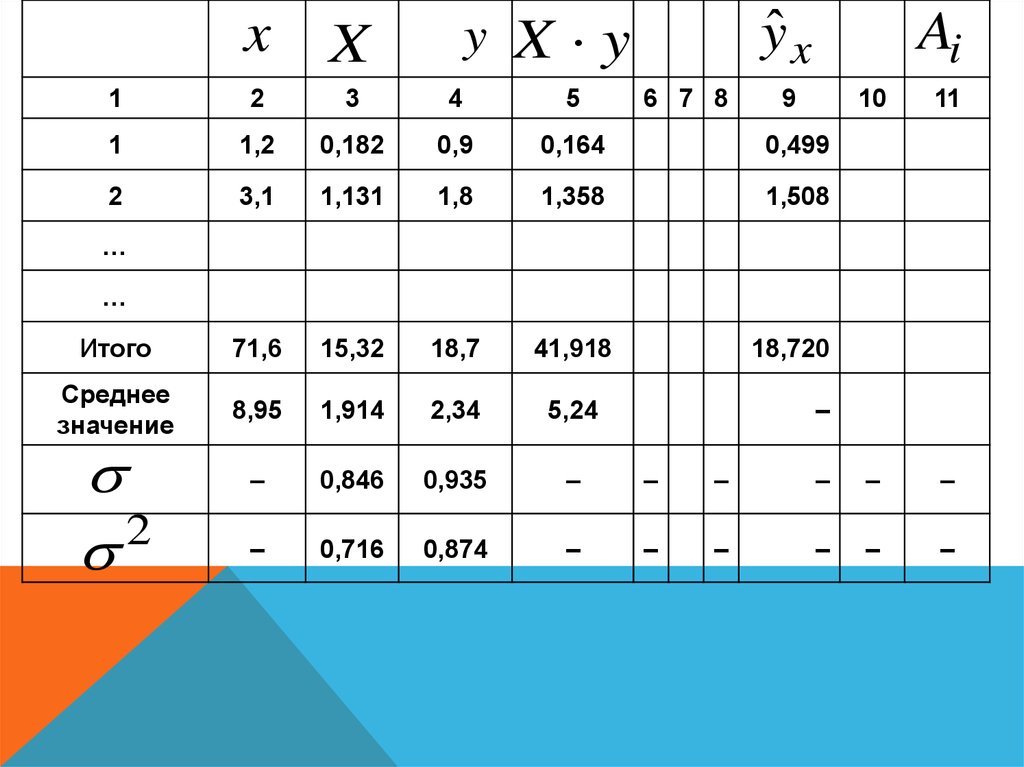
yˆ xy X y
Ai
x
X
1
2
3
4
5
1
1,2
0,182
0,9
0,164
0,499
2
3,1
1,131
1,8
1,358
1,508
Итого
71,6
15,32
18,7
41,918
18,720
Среднее
значение
8,95
1,914
2,34
5,24
–
0,846
0,935
–
–
–
–
0,716
0,874
–
–
–
6 7 8
9
10
11
–
–
–
–
–
–
…
…
2
–
16.
bcov(X , y )
2
X
5,24 1,914 2,34
1,063
0,716
a y b X 2,34 1,063 1,914 0,305
y x 0,305 1,063 ln x
17.
2ост
0,0711
xy 1 2 1
0,958
y
0,874
0,918
2
xy
F
2
xy
2
1 xy
Fтабл 5,99
A 14,51%
n m 1
0,918 8 1 1
67,17
m
1 0,918
1
k1 1
k2 n 2 6
0,05
Fфакт Fтабл
18.
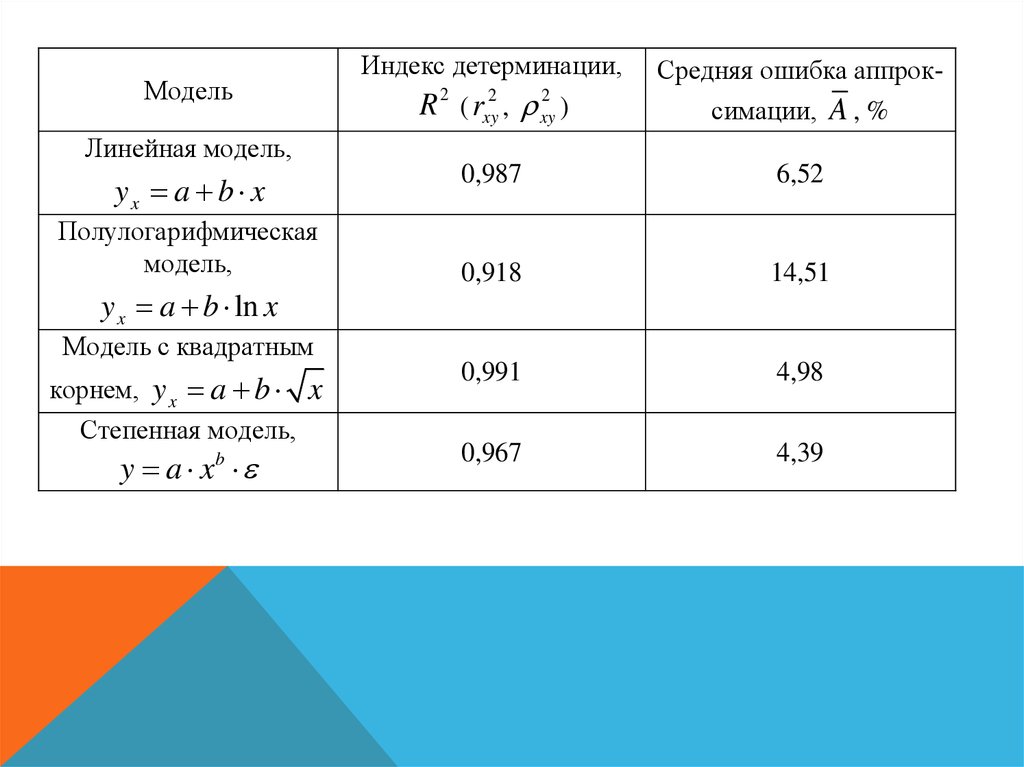
МодельИндекс детерминации,
R 2 ( rxy2 , xy2 )
Средняя ошибка аппроксимации, A , %
0,987
6,52
0,918
14,51
0,991
4,98
0,967
4,39
Линейная модель,
yx a b x
Полулогарифмическая
модель,
y x a b ln x
Модель с квадратным
корнем, y x a b x
Степенная модель,
y a xb











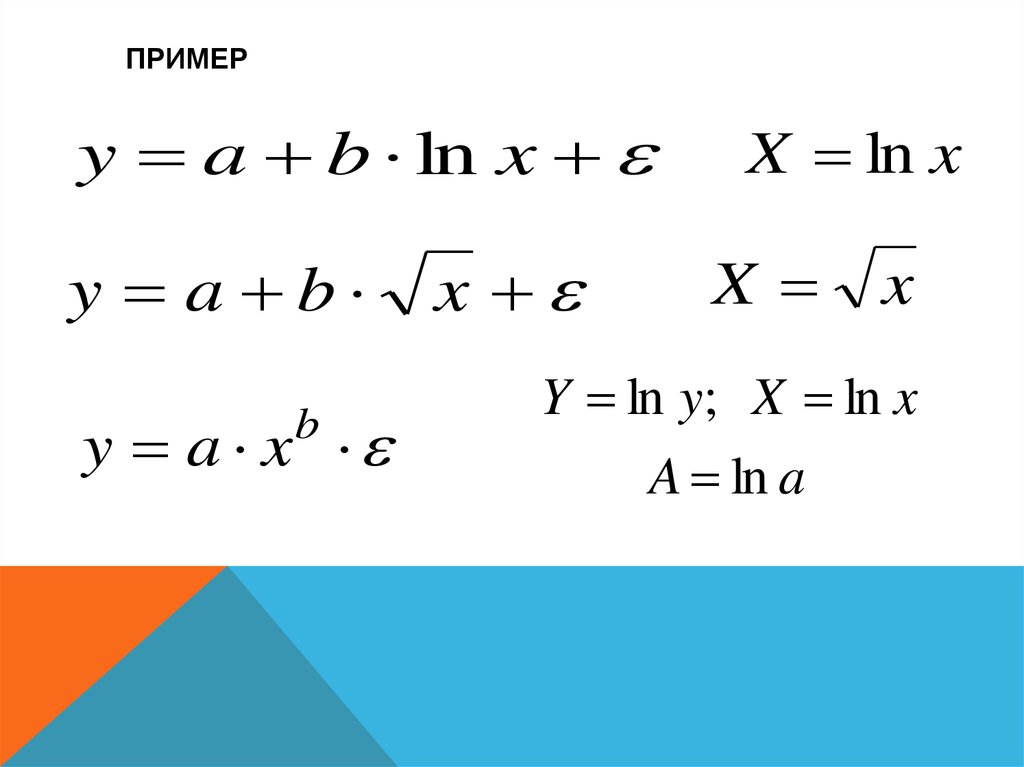
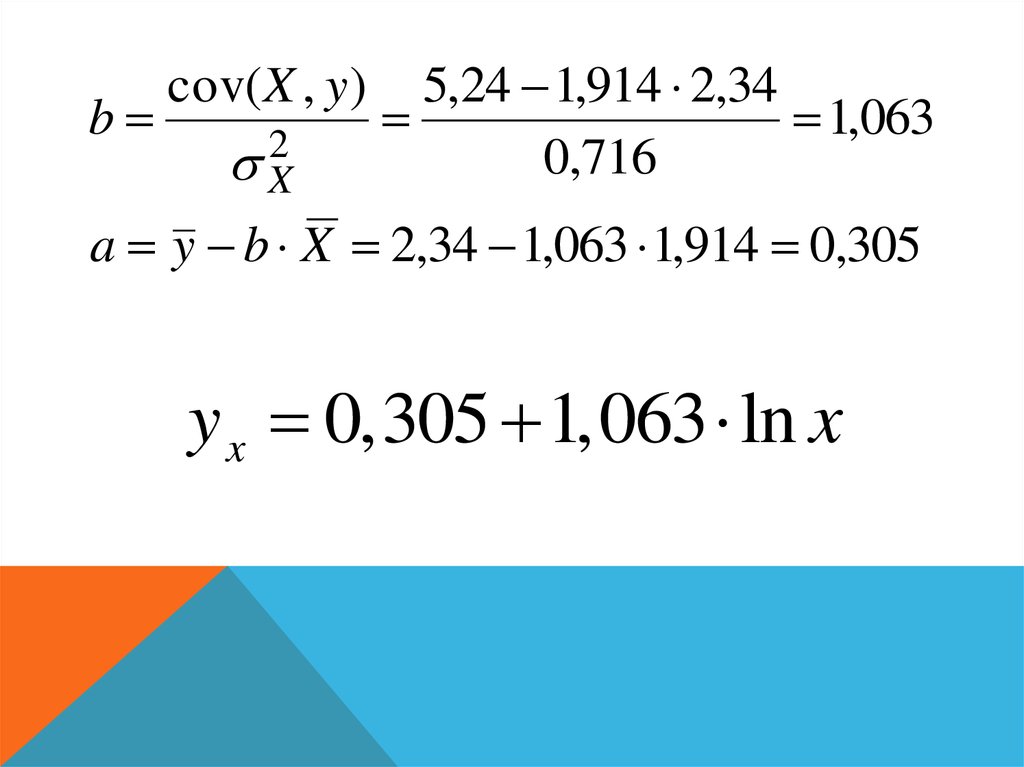

 mathematics
mathematics








