Similar presentations:
Нелинейная регрессия
1. Тема 3. Нелинейная регрессия. 1. Примеры нелинейной регрессии. 2. Методы преобразования полиноминального уравнения регрессии. 3. Преобразова
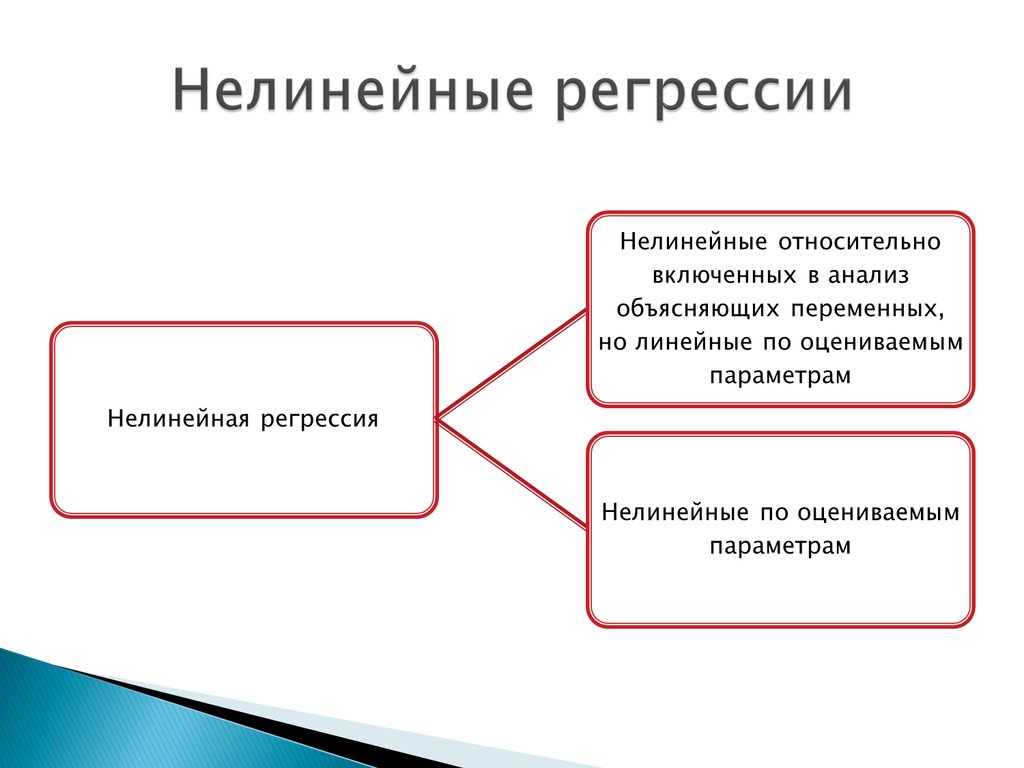
2. Нелинейные регрессии
3.
4.
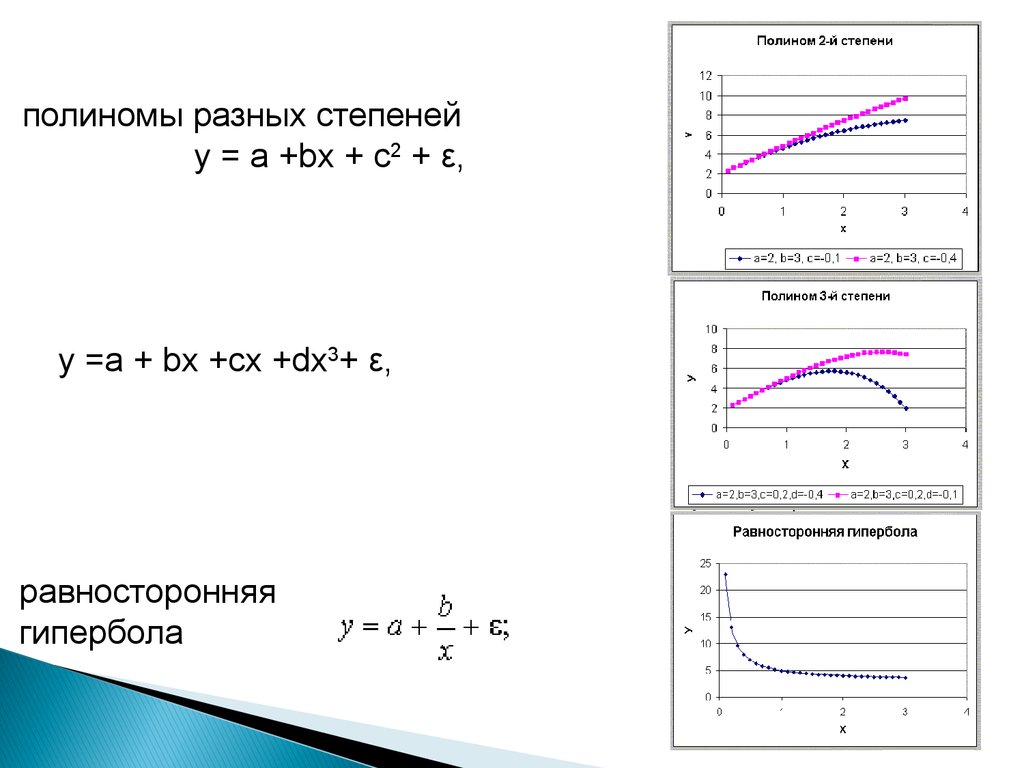
полиномы разных степенейу = а +bх + с2 + ε,
у =а + bх +сх +dx3+ ε,
равносторонняя
гипербола
5.
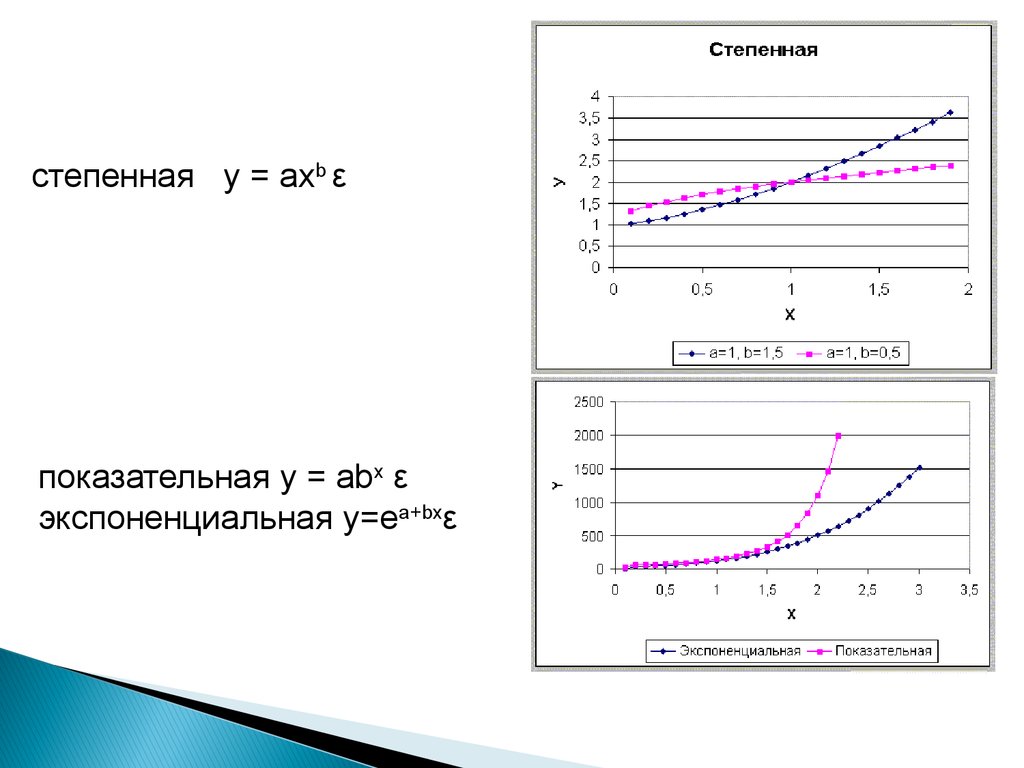
степенная y = axb εпоказательная у = аbх ε
экспоненциальная y=ea+bxε
6.
В параболе второй степениу= а0 + а1 х + а2 х2 + ε
заменяя переменные х1 =х, х2 = х2, получим двухфакторное
уравнение линейной регрессии:
у= а0 + а1 х1 + а2 х2 + ε
для оценки параметров которого используется МНК.
Соответственно для полинома третьего порядка
y= a0+a1x+a2x2+a3x3+ ε,
при замене х=х1, х2=х2, х3=х3 получим трехфакторную модель
линейной регрессии:
у= а0 + а1 х1 + а2 х2 + а3 х3 + ε,
Для полинома k-порядка
y= a0+a1x+a2x2+…+akxk+ ε
получим линейную модель множественной регрессии
объясняющими переменными:
у= а0 + а1 х1 + а2 х2 + …+ аk хk + ε
с
k
7.
Приравниваем к нулю первую производную параболы второй степени.Применение МНК для оценки параметров параболы второй степени
приводит к следующей системе нормальных уравнений:
8.
равносторонняя гиперболакривая Филлипса
Для равносторонней гиперболы такого вида, заменив
1/х на z, получим линейное уравнение регрессии
y = a +bz +ε
оценка параметров которого может быть дана МНК.
9.
Система нормальных уравнений составит:10.
В отдельных случаях может использоваться и нелинейнаямодель вида
Но, если в равносторонней гиперболе
подвергается объясняющая переменная
z = 1/x и y = а + bz + ε,
преобразованию
то для получения линейной формы зависимости в обратной
модели преобразовывается у, а именно:
z =1/y и z = a + bx +ε.
В результате обратная модель оказывается внутренне
нелинейной и требование МНК выполняется не для
фактических значений признака у, а для их обратных величин
1/у, а именно
11. Линеаризация
2$
y
a
b
x
c
x
Парабола
x
Гипербола
X 1
x
$
yx a b x
b
yX y
X
X (X )
2
2
x x1 , x 2 x2
a y bX
$
Полулогарифмическая функция y x a b ln x
Х=lnx
b
yX y
X
X 2 ( X )2
a y bX
12.
Модели, нелинейные по параметрам-нелинейные модели внутренне линейные
- нелинейные модели внутренне нелинейные.
13.
yx axb
yx a
bx
y x a eb x
1
yx
a b
x
a
yx
1 b
e c x
yx a b
x
c
1
yx a
1
b
1 x
14.
в эконометрических исследованиях при изучении эластичности спросаот цен широко используется степенная функция:
y = axbε
где у – спрашиваемое количество;
х – цена;
ε – случайная ошибка.
логарифмирование данного уравнения по основанию ε приводит его
к линейному виду:
lnу = lnа + b lnx + ln ε.
Если же модель представить в виде
y = axbε,
то она становится внутренне нелинейной, т.к. ее невозможно
превратить в линейный вид. Внутренне нелинейной будет и модель
вида
у = а + bхc + ε,
или модель
15.
В этом плане к линейнымэкспоненциальную модель
относят,
например,
y = еa+bхε,
т.к. логарифмируя ее по натуральному основанию,
получим линейную форму модели
lnу = а + b х +lnε.
16.
Модели внутренне нелинейные по параметрам могут иметь место вэконометрических исследованиях. Среди них можно назвать и
обратную модель вида:
17.
18.
В степенной функцииy = axbε.
параметр b является коэффициентом эластичности. Его
величина, на сколько процентов изменится в среднем
результат, если фактор изменится на 1%.
Формула расчета коэффициента эластичности:
19.
20.
21. Формулы для расчета среднего коэффициента эластичности
Вид функции,y
y a b
x
y a b
x c
x2
b
y a
x
Средний коэффициент эластичности,
b
x
a b
x
b 2c x x
a b
x c
x2
b
a
x b
y a
xb
b
y a
b
x
ln b
x
Ý
22. Формулы для расчета среднего коэффициента эластичности
Вид функции,y
Средний коэффициент эластичности,
y a b
ln x
b
a b
ln x
y e a bx
x
b
1
y
a b
x
b
c x
b ec x
b
x
a b
x
a
y
1 b
e c x
Ý
23.
Если в линейной модели и моделях, нелинейных по переменным, приоценке параметров исходят из критерия
то в моделях, нелинейных по оцениваемым параметрам, требование
МНК применяется не к исходным данным результативного признака, а к
их преобразованным величинам, т. е. lnу, 1/у.
Так, в степенной функции y = axbε
МНК применяется к преобразованному уравнению
lnу = lnа + xlnb.
Это значит, что оценка параметров основывается на минимизации
суммы квадратов отклонений в логарифмах:
Соответственно, если в линейных моделях (включая нелинейные по
переменным ∑(y-ŷх) =0, то в моделях, нелинейных по оцениваемым
параметрам,
24.
Корреляция для нелинейной регрессии25.
xy2
y
y
x
1
2
y
y
2
ост
1 2
y
Для равносторонней гиперболы
индекс корреляции
Линейный
коэффициент
переменными y и lnx
корреляции
между
26.
27.
Ошибка разности между индексом детерминации R2yx икоэффициентом детерминации r2yx:
Ошибка аппроксимации
28. Нелинейные модели внутренне линейные
Степенная у=ахbY=ln y, X=ln x, A=ln a
b
YX Y X
X (X )
2
2
A Y bX
Показательная у=аbх
Yx Y x
Y=lny, В=lnb, A=lna
B
2
2
A Y Bx
Экспоненциальная у=аеbх
Yx Y x
Y=lny, A=lna
b
A Y bx
x (x)
Обратная
Y=1/y
1
$
yx
a b x
b
x (x)
2
2
Yx Y x
x 2 (x) 2
à Y bx

























 mathematics
mathematics








