Прямая. Прямые общего и частного положения

1. Прямая

ПРЯМАЯ
Лекция 2
1

2. ПРЯМАЯ

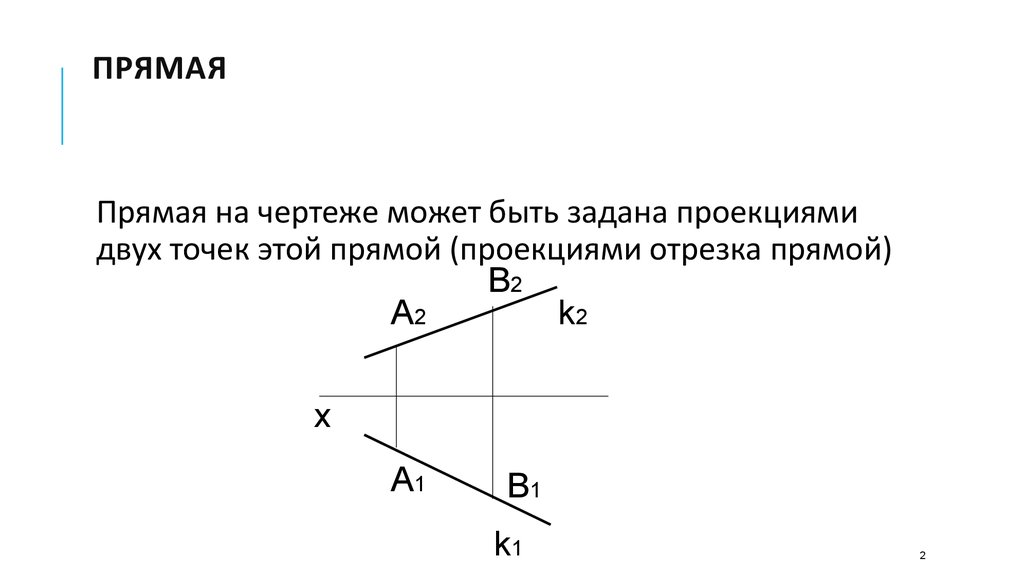
Прямая на чертеже может быть задана проекциями
двух точек этой прямой (проекциями отрезка прямой)
В2
A2
k2
x
A1
В1
k1
2

3. ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ

Прямая общего положения не имеет проекций,
параллельных или перпендикулярных осям
координат
Прямые частного положения
1. Прямая параллельна одной плоскости
проекций*
2. Прямая параллельна двум плоскостям
проекций*
*В первом случае одна проекция отрезка прямой
равна самому отрезку. Во втором случае две
проекции отрезка равны ему
3

4. Пример построения проекций прямой

ПРИМЕР ПОСТРОЕНИЯ ПРОЕКЦИЙ ПРЯМОЙ
zz
B2
B3
A3
y = 40
y = 20
z = 30
z = 40
A2
xx
y
B1
A1
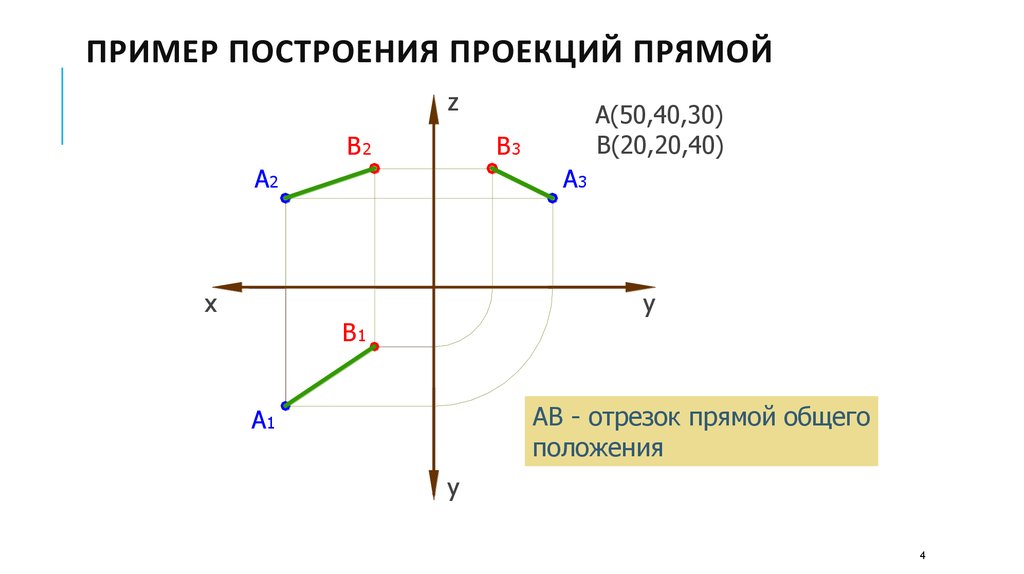
A(50,40,30)
B(20,20,40)
АВ - отрезок прямой общего
положения
x=
x=
2050
y
4

5. Вопрос 1

ВОПРОС 1
Назовите способы задания отрезка прямой

6. Прямая параллельная одной плоскости проекций

ПРЯМАЯ ПАРАЛЛЕЛЬНАЯ ОДНОЙ ПЛОСКОСТИ
ПРОЕКЦИЙ
Горизонтальная прямая – параллельна
горизонтальной плоскости проекций
Фронтальная прямая – параллельна фронтальной
плоскости проекций
Профильная прямая – параллельна профильной
плоскости проекций
Перечисленные прямые также называют прямыми
уровня
6

7. Горизонтальная прямая

ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ
z
A2
B2
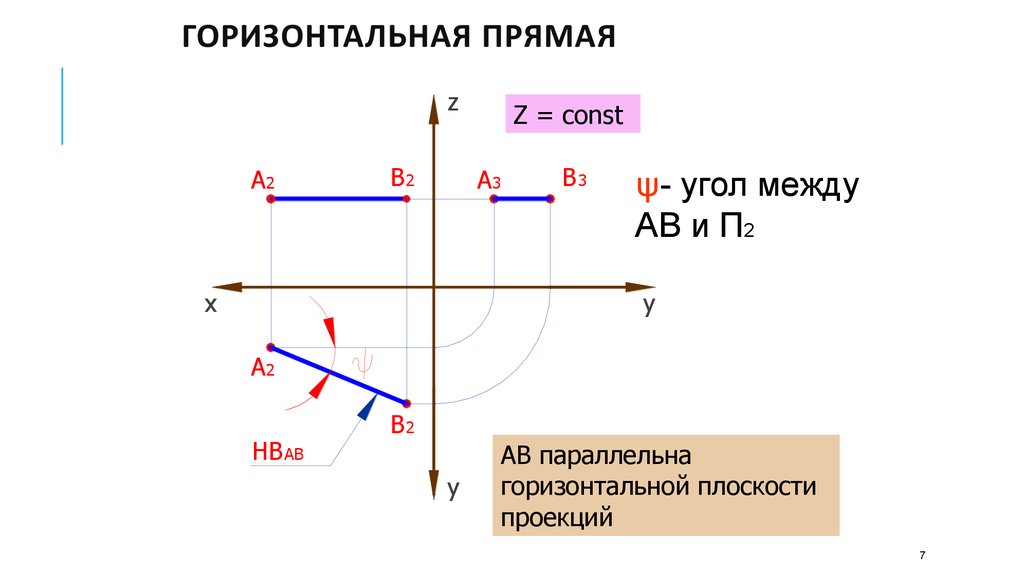
Z = const
A3
x
B3
ψ- угол между
АВ и П2
y
A2
HB AB
B2
y
АВ параллельна
горизонтальной плоскости
проекций
7

8. Фронтальная прямая

ФРОНТАЛЬНАЯ ПРЯМАЯ
A2
z
HB AB
A3
B2
B3
x
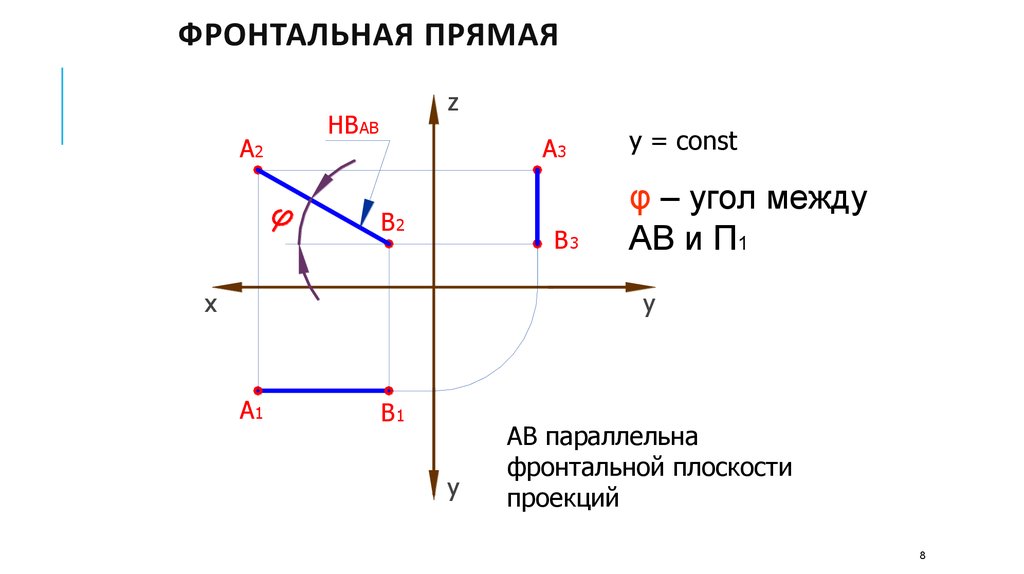
y = const
φ – угол между
АВ и П1
y
A1
B1
y
АВ параллельна
фронтальной плоскости
проекций
8

9. Профильная прямая

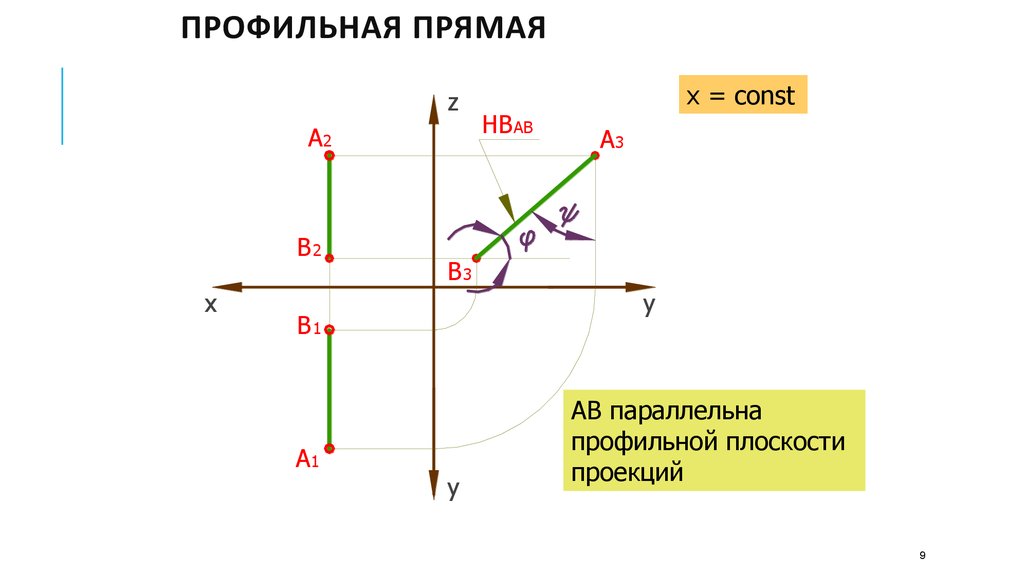
ПРОФИЛЬНАЯ ПРЯМАЯ
z
A2
B2
x
A3
B3
y
B1
A1
HB AB
x = const
y
АВ параллельна
профильной плоскости
проекций
9

10. Вопрос 2

ВОПРОС 2
Какая из проекций фронтальной прямой дает её
натуральную величину?

11. Прямая параллельна двум плоскостям проекций

ПРЯМАЯ ПАРАЛЛЕЛЬНА ДВУМ ПЛОСКОСТЯМ
ПРОЕКЦИЙ
1. Прямая параллельна плоскостям П1и П2 , т.е.
перпендикулярна плоскости П3 – профильнопроецирующая прямая
2. Прямая параллельна плоскостям П1 и П3 , т.е.
перпендикулярна плоскости П2 – фронтальнопроецирующая прямая
3. Прямая параллельна плоскостям П2 и П3 , т.е.
перпендикулярна плоскости П1 – горизонтальнопроецирующая прямая
11

12. Горизонтально-проецирующая прямая

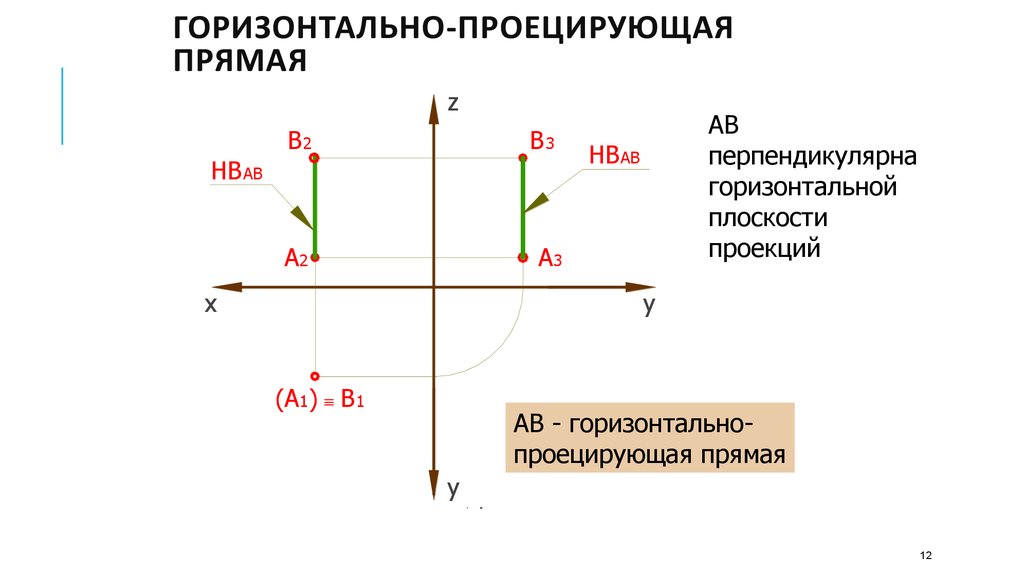
ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ
ПРЯМАЯ
z
B2
HB AB
z
A2
B3
АВ
перпендикулярна
горизонтальной
плоскости
проекций
HB AB
A3
x
y
x
y
A11 ) B 1B 1
(A
АВ - горизонтальнопроецирующая прямая
y y
12

13. Фронтально-проецирующая прямая

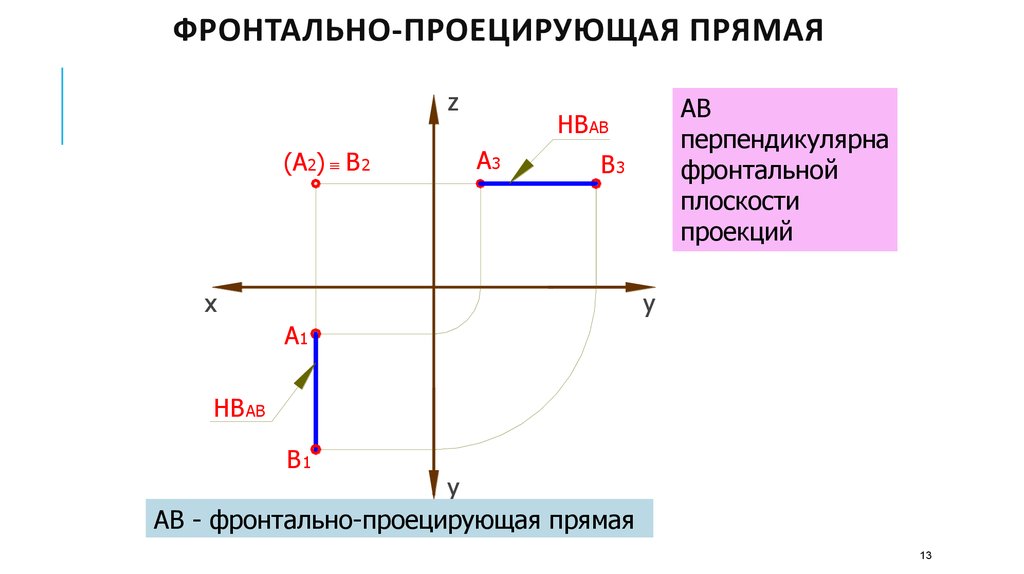
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
z
A22 ) B 2B 2
(A
АВ
перпендикулярна
фронтальной
плоскости
проекций
HB AB
A
z3
B3
x
y
xA1
y
HB AB
B1
y y
АВ - фронтально-проецирующая прямая
13

14. Профильно-проецирующая прямая

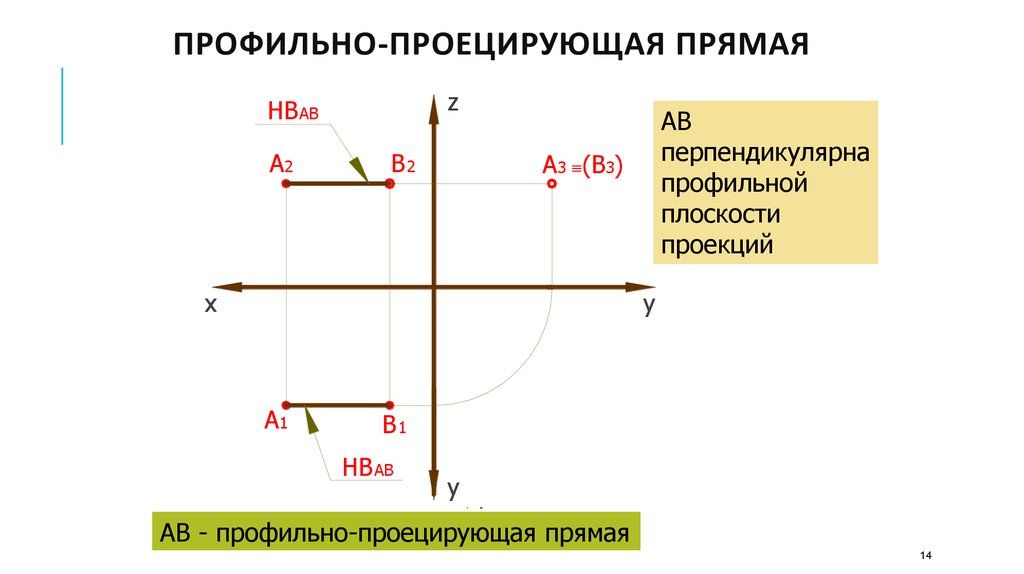
ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
z
HB AB
A2
B2
z
АВ
перпендикулярна
профильной
плоскости
проекций
B 33)
A3 (B
x
y
x
A1
y
B1
HB AB
y y
АВ - профильно-проецирующая прямая
14

15. ВОПРОС 3

Какая из проекций горизонтальной прямой
параллельна оси Х?

16. Следы прямой

СЛЕДЫ ПРЯМОЙ
Точки пересечения прямой линии с плоскостями
проекции называются следами прямой
Точка пересечения прямой с горизонтальной
плоскостью проекций называется
горизонтальным следом прямой
Точка пересечения прямой с фронтальной
плоскостью проекций называется фронтальным
следом прямой
16

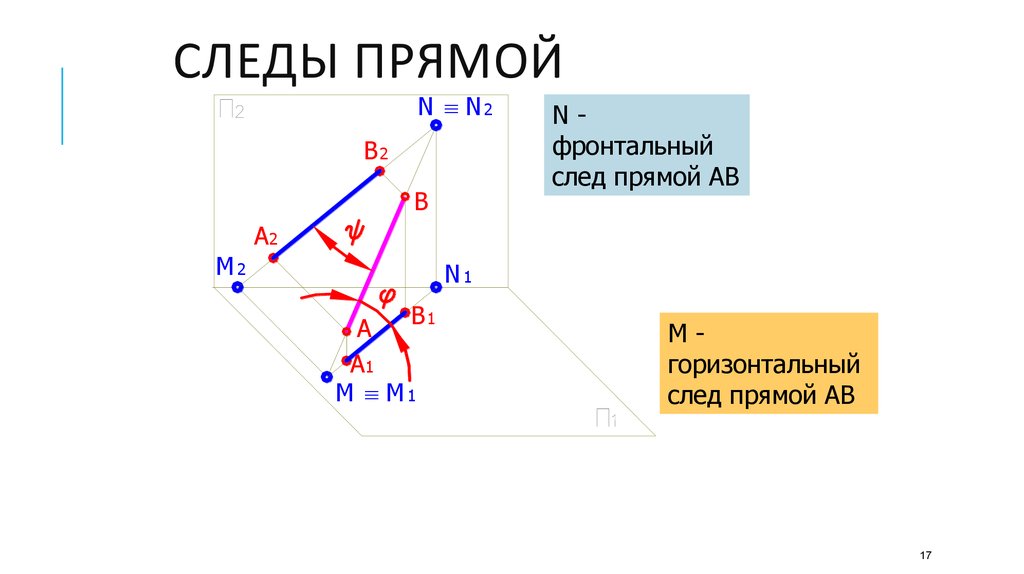
17. Следы прямой

СЛЕДЫ ПРЯМОЙ
N N 2
B2
B
M 2
Nфронтальный
след прямой АВ
A2
N 12
B1
A
A1
M M 1
Мгоризонтальный
след прямой АВ
17

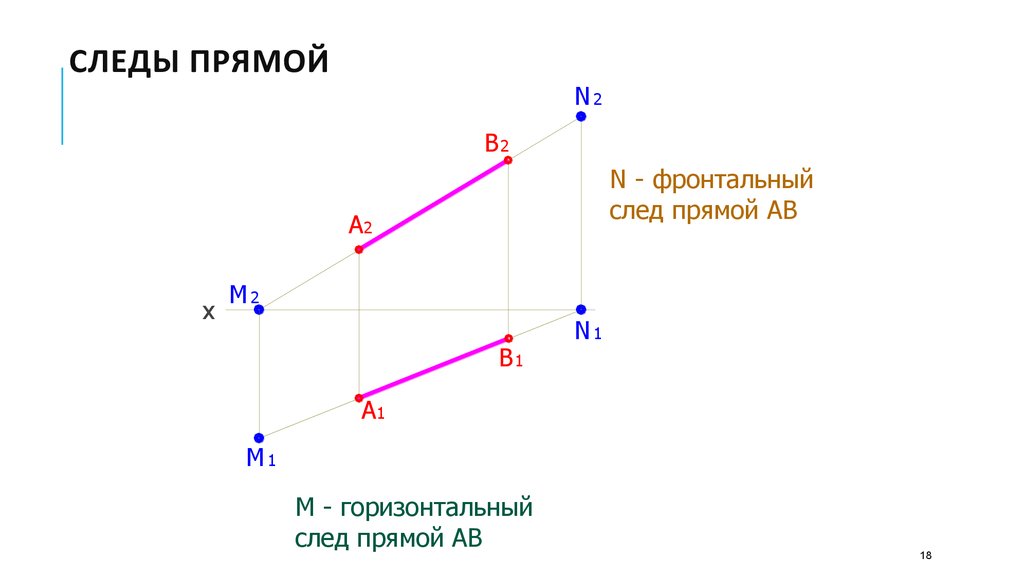
18. Следы прямой

СЛЕДЫ ПРЯМОЙ
N2
B22
B
N - фронтальный
след прямой АВ
A22
A
M22
M
xx
B11
B
N11
N
A11
A
M11
M
М - горизонтальный
след прямой АВ
18

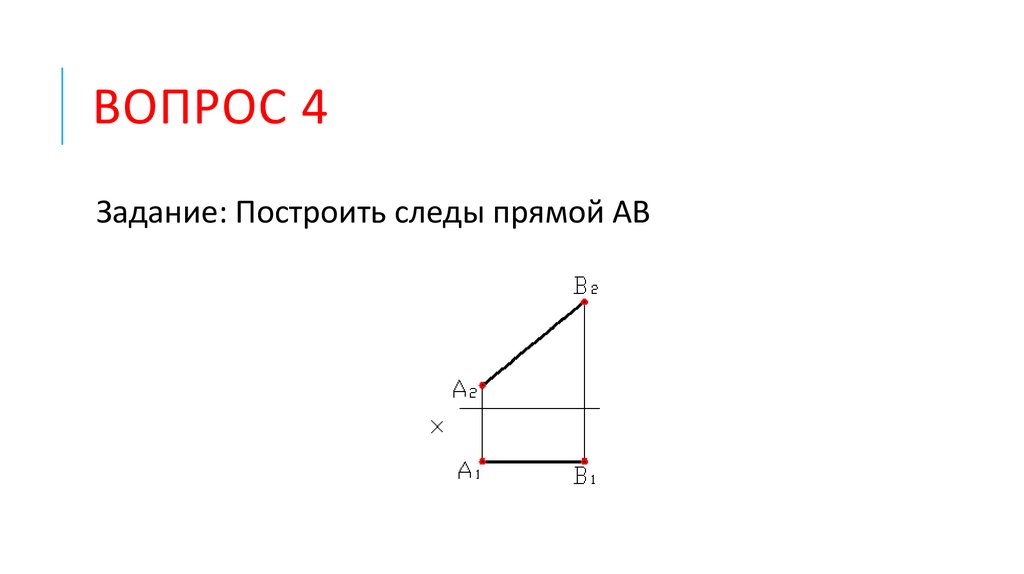
19. ВОПРОС 4

Задание: Построить следы прямой АВ

20. Способы задания прямой

СПОСОБЫ ЗАДАНИЯ ПРЯМОЙ
1. По координатам точек концов отрезка прямой (проекциям
отрезка прямой).
2. Параметрами отрезка прямой линии:
- натуральной величиной отрезка (НВ);
- углами наклона к плоскостям проекций - (П₁) и (П₂);
- угол между линией отрезка и горизонтальной плоскостью
(П₁);
- угол между линией отрезка и фронтальной плоскостью
(П₂).
20

21. Способ прямоугольного треугольника

СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Натуральная величина отрезка прямой общего
положения равна гипотенузе прямоугольного
треугольника, одним катетом которого является
проекция отрезка на любую плоскость проекций,
другим – разность расстояний концов отрезка до
той же плоскости проекций
21

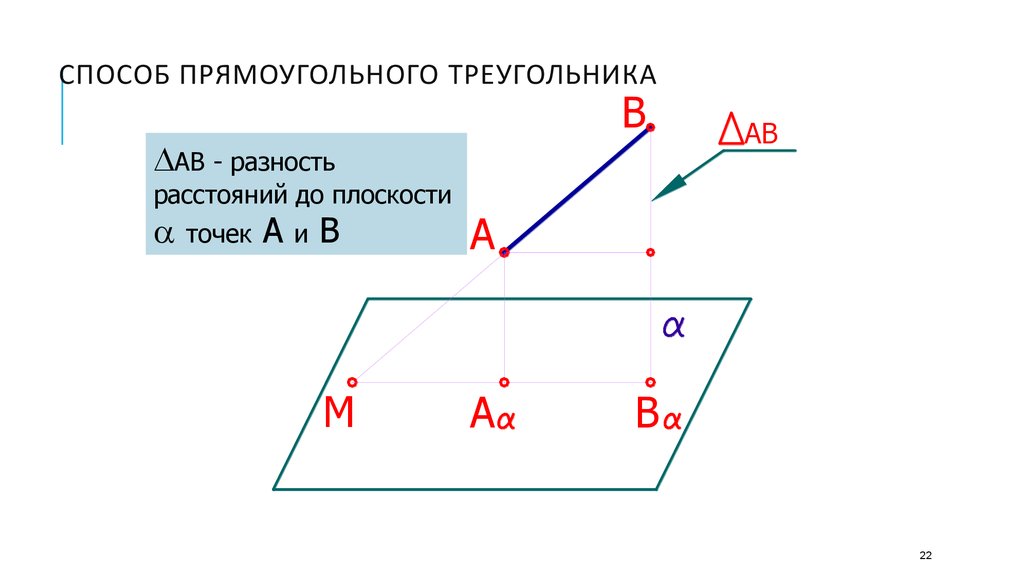
22. Способ прямоугольного треугольника

СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
B
АВ - разность
расстояний до плоскости
точек
А
и
В
M
A
B
AB
A
A
B
22

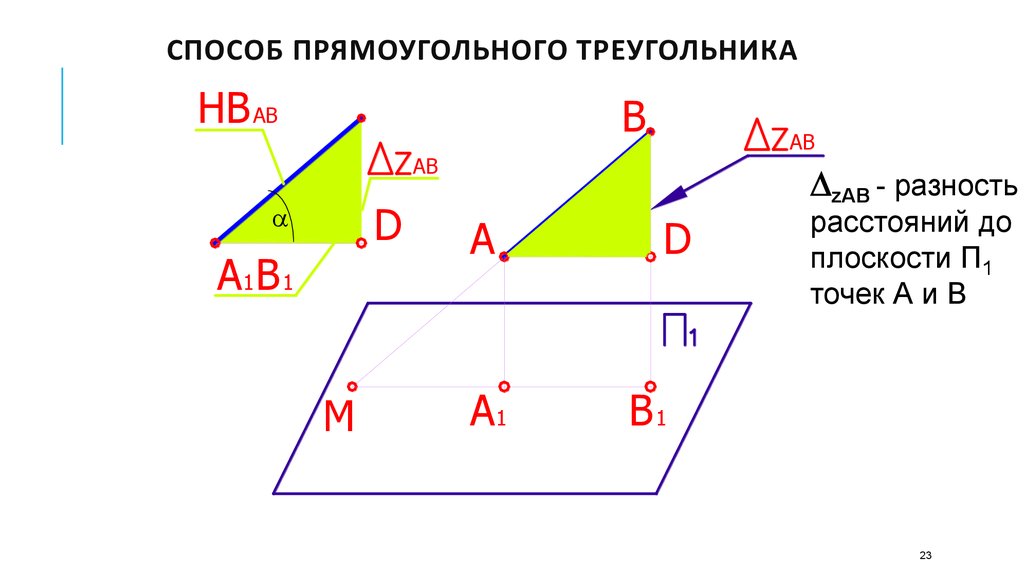
23. Способ прямоугольного треугольника

СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
HB AB
B
AB
AB
AB
D
A1 B 1
M
zАВ - разность
A
A11
D
расстояний до
плоскости П1
точек А и В
B 11
23

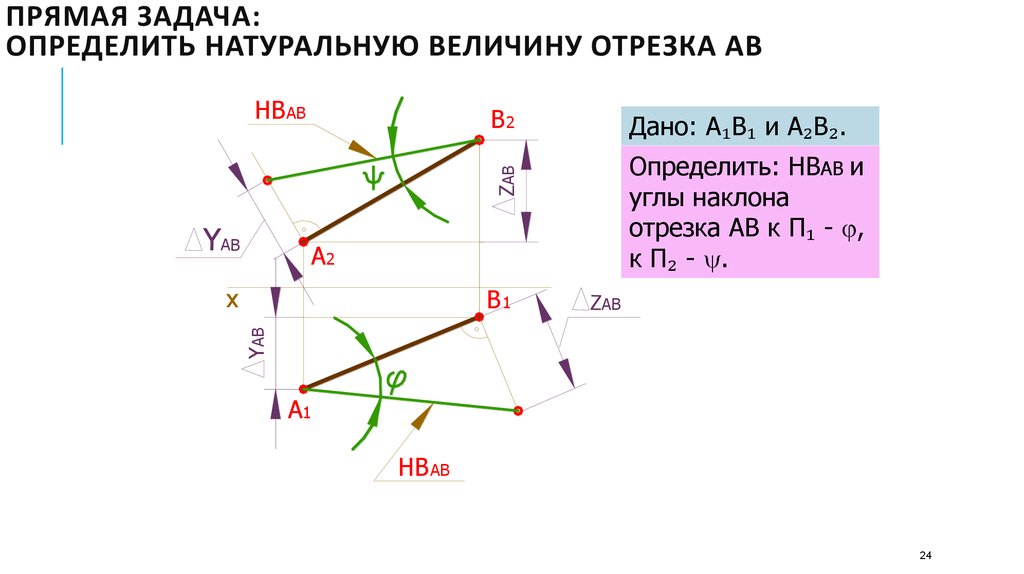
24. Прямая задача: определить натуральную величину отрезка АВ

ПРЯМАЯ ЗАДАЧА:
ОПРЕДЕЛИТЬ НАТУРАЛЬНУЮ ВЕЛИЧИНУ ОТРЕЗКА АВ
HB AB
B2
Дано: А₁В₁ и А₂В₂.
ZAB
Определить: НВАВ и
углы наклона
отрезка АВ к П₁ - ,
к П₂ - .
YAB
A2 A2
x
ZAB
YAB
B1
A1
A1
HB AB
24

25. Способ прямоугольного треугольника. Обратная задача

СПОСОБ ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА.
ОБРАТНАЯ ЗАДАЧА
Лекция 3

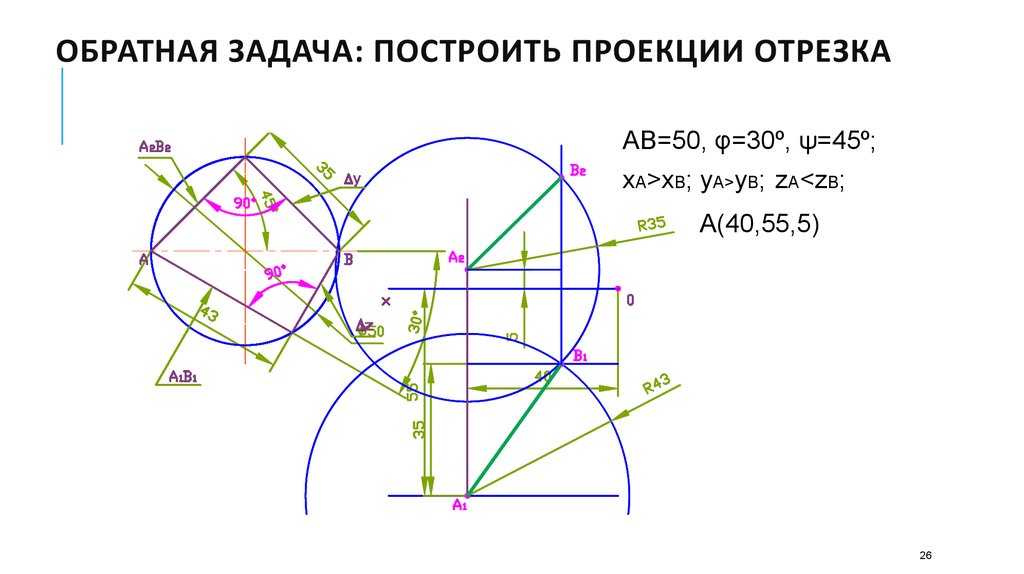
26. Обратная задача: построить проекции отрезка

ОБРАТНАЯ ЗАДАЧА: ПОСТРОИТЬ ПРОЕКЦИИ ОТРЕЗКА
АВ=50, φ=30º, ψ=45º;
xA>xB; yA>yB; zA<zB;
y
А(40,55,5)
zz
26

27. Вопрос 5

ВОПРОС 5
Для чего служит способ прямоугольного
треугольника?

28. Относительное положение прямых

ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
По расположению относительно друг друга прямые
могут:
быть параллельными
пересекаться
скрещиваться
У скрещивающихся прямых одноименные
проекции прямых пересекаются, но точки
пересечения не лежат на одной линии связи
28

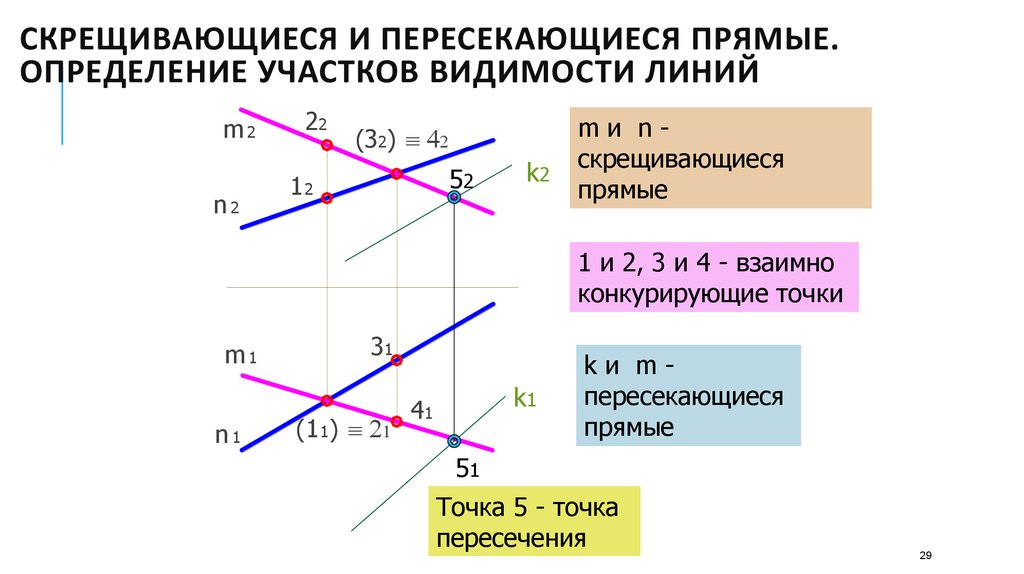
29. Скрещивающиеся и пересекающиеся прямые. Определение участков видимости линий

СКРЕЩИВАЮЩИЕСЯ И ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ.
ОПРЕДЕЛЕНИЕ УЧАСТКОВ ВИДИМОСТИ ЛИНИЙ
m2
n2
22
(32)
52
12
k2
mи nскрещивающиеся
прямые
1 и 2, 3 и 4 - взаимно
конкурирующие точки
m1
n1
31
1 11 )
(1
k1
41
kи mпересекающиеся
прямые
51
Точка 5 - точка
пересечения
29

30. ВЫВОДЫ

По положению относительно плоскостей проекций
различают:
прямые общего положения (непараллельные и
неперпендикулярные плоскостям проекций)
прямые частного положения: параллельные или
перпендикулярные плоскостям проекций
Способ прямоугольного треугольника позволяет
решать метрические и позиционные задачи в
отношении отрезков прямой общего положения
30

31. ВЫВОДЫ

Прямые частного положения и их отрезки на
соответствующих проекциях дают натуральные
величины и углы расположения относительно
плоскостей проекций
Плоскости частного положения позволяют получить
натуральную величину или угол наклона к
плоскости проекций
31