Similar presentations:
Проекции отрезков прямой
1. Проекции отрезков прямой
Лекция 2Проекции
отрезка прямой
Прямые частного положения
Определение натуральной величины (НВ)
отрезка
Способ прямоугольного треугольника
Относительное положение прямых.
1
2. ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
Прямая общего положения не имеетпроекций, параллельных или
перпендикулярных осям координат.
Прямые частного положения
параллельны или перпендикулярны
относительно какой-либо плоскости
проекций.
Параллельные прямые – линии уровня.
Такие прямые имеют проекции,
параллельные или перпендикулярные
осям координат.
2
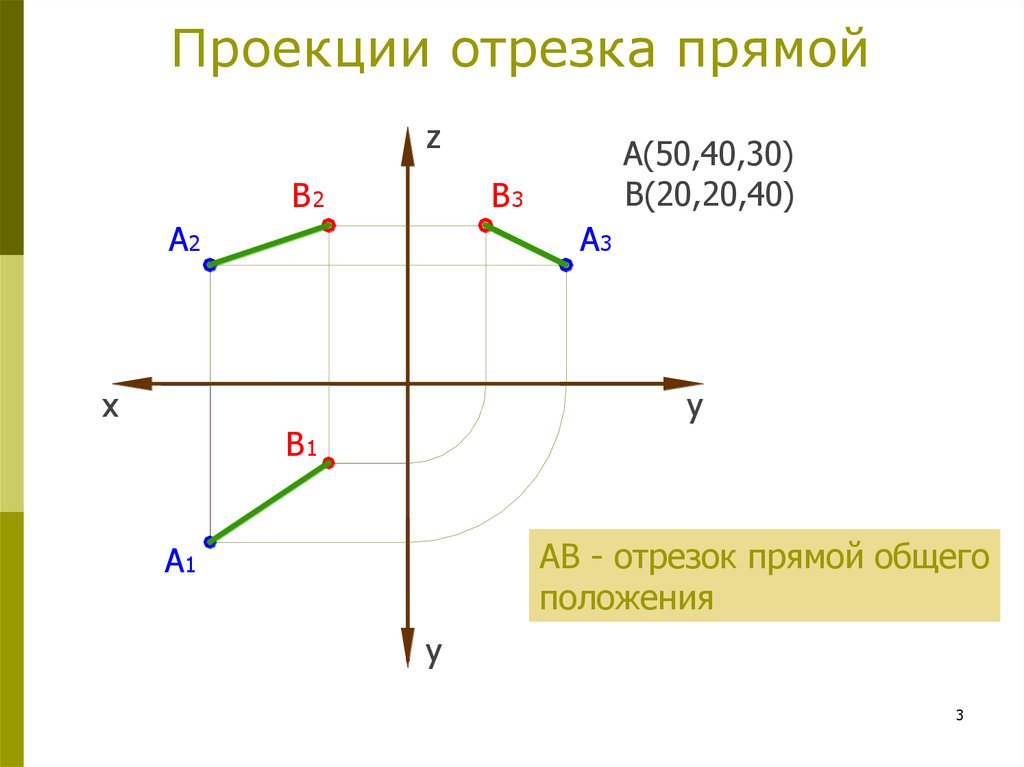
3. Проекции отрезка прямой
zzB2
B3
A3
y = 40
y = 20
z = 30
z = 40
A2
xx
y
B1
A1
A(50,40,30)
B(20,20,40)
АВ - отрезок прямой общего
положения
x=
x=
2050
y
3
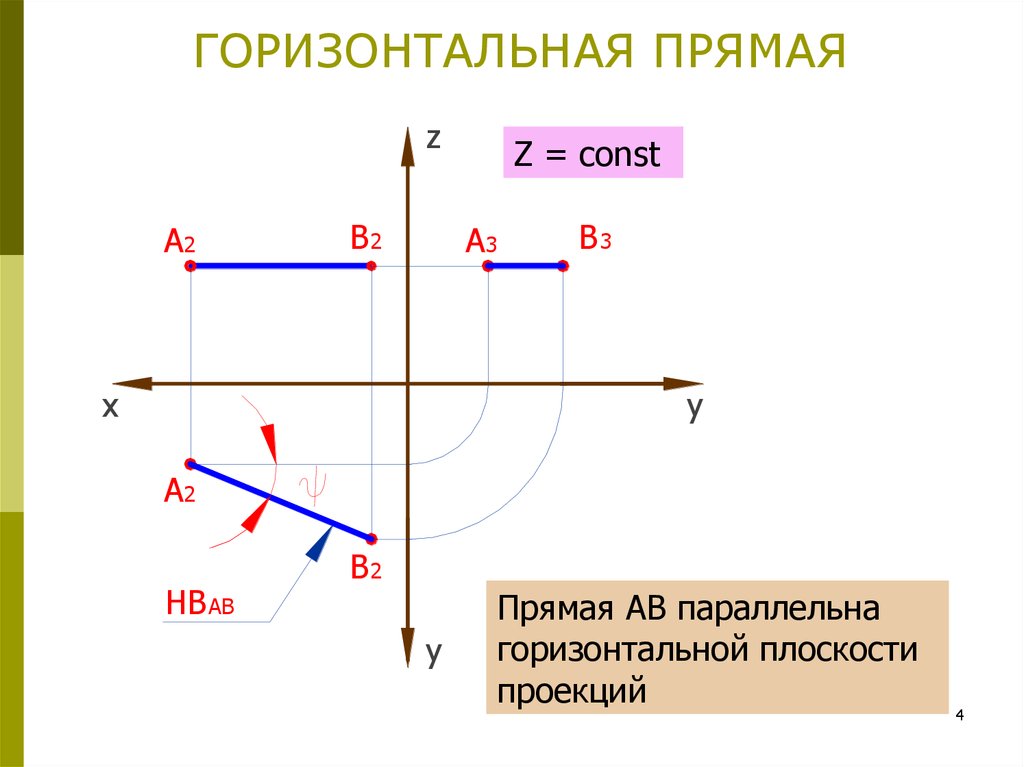
4. ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ
zA2
B2
Z = const
A3
x
B3
y
A2
HB AB
B2
y
Прямая АВ параллельна
горизонтальной плоскости
проекций
4
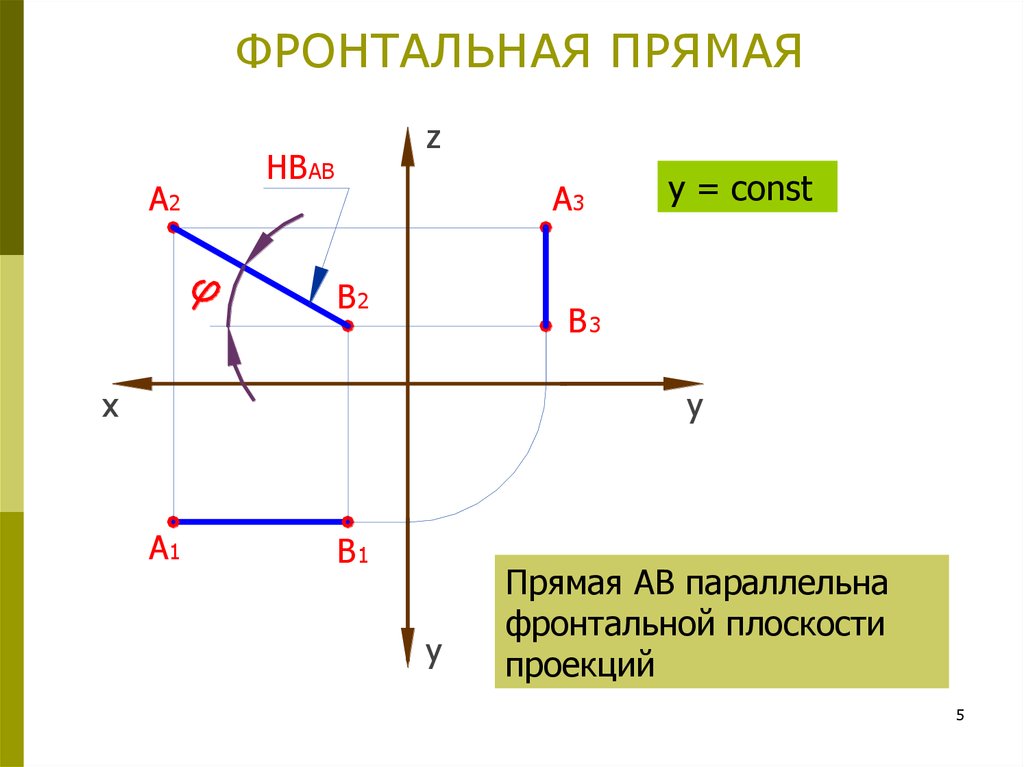
5. ФРОНТАЛЬНАЯ ПРЯМАЯ
A2z
HB AB
A3
B2
y = const
B3
x
y
A1
B1
y
Прямая АВ параллельна
фронтальной плоскости
проекций
5
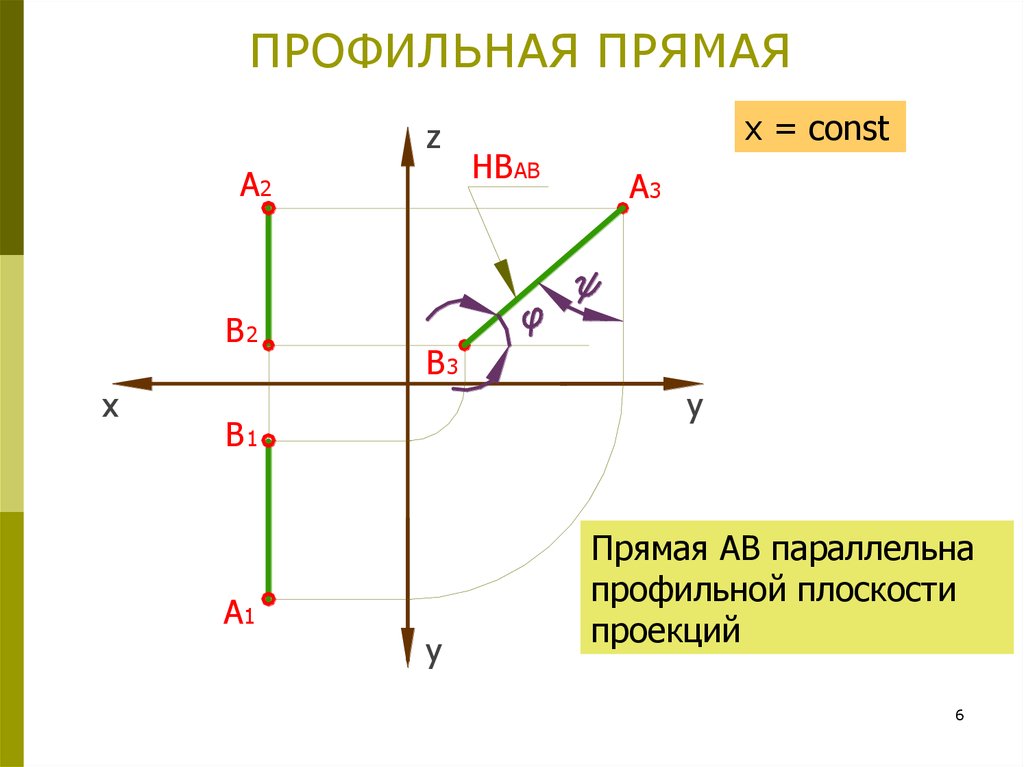
6. ПРОФИЛЬНАЯ ПРЯМАЯ
zA2
B2
x
A3
B3
y
B1
A1
HB AB
x = const
y
Прямая АВ параллельна
профильной плоскости
проекций
6
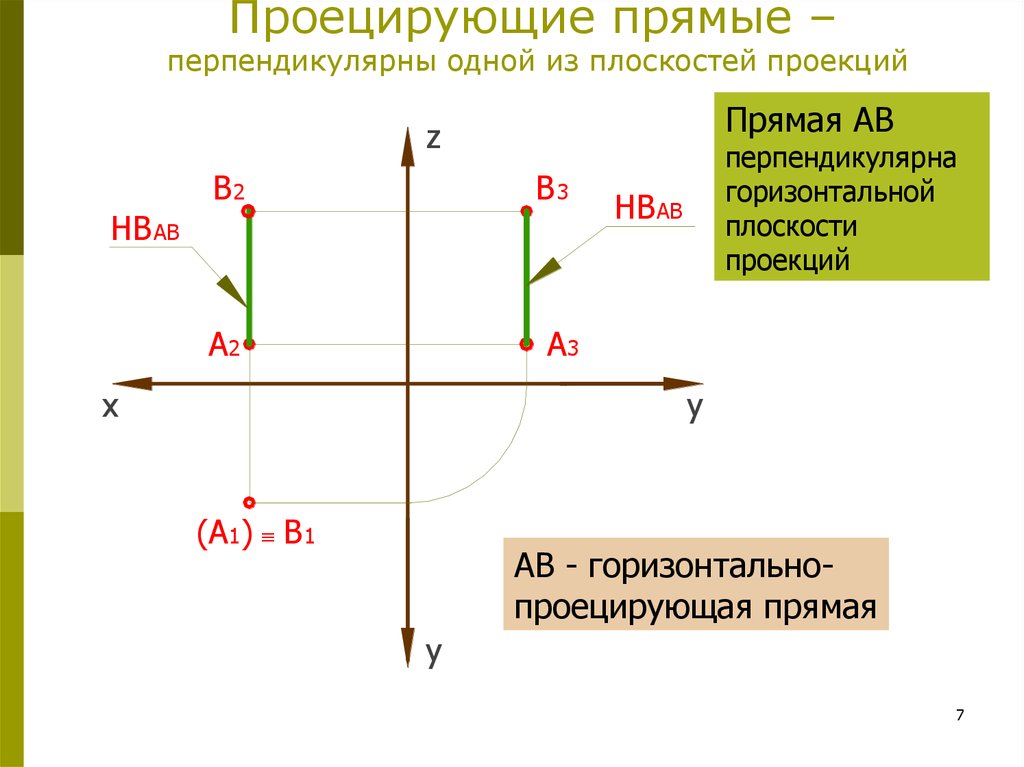
7. Проецирующие прямые – перпендикулярны одной из плоскостей проекций
Прямая АВz
B2
B3
HB AB
A2
перпендикулярна
горизонтальной
плоскости
проекций
HB AB
A3
x
y
A11 ) B 1B 1
(A
АВ - горизонтальнопроецирующая прямая
y
7
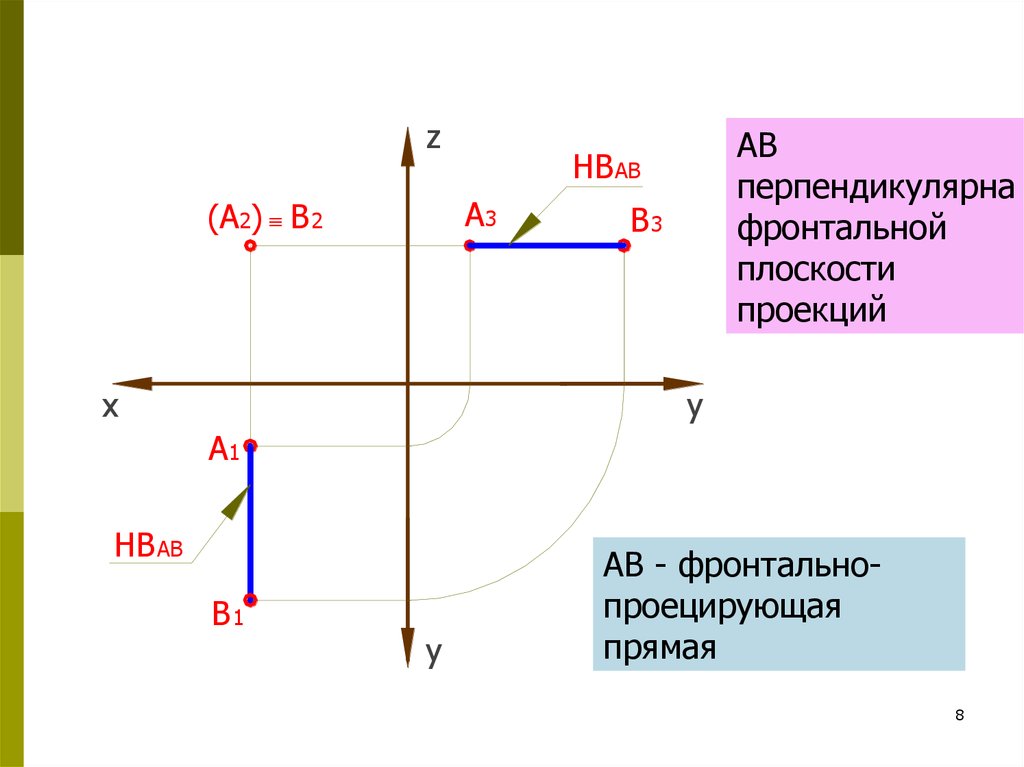
8.
zHB AB
A3
A22 ) B 2B 2
(A
x
АВ
перпендикулярна
фронтальной
плоскости
проекций
B3
y
A1
HB AB
B1
y
АВ - фронтальнопроецирующая
прямая
8
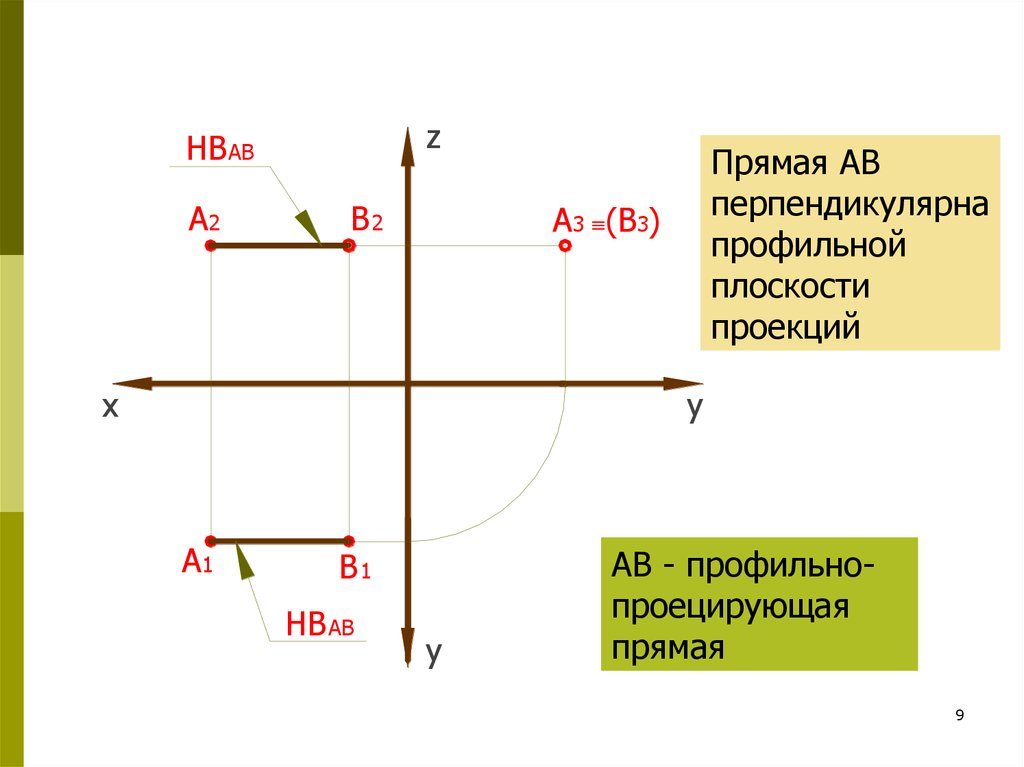
9.
zHB AB
A2
B2
Прямая АВ
перпендикулярна
профильной
плоскости
проекций
B 33)
A3 (B
x
y
A1
B1
HB AB
y
АВ - профильнопроецирующая
прямая
9
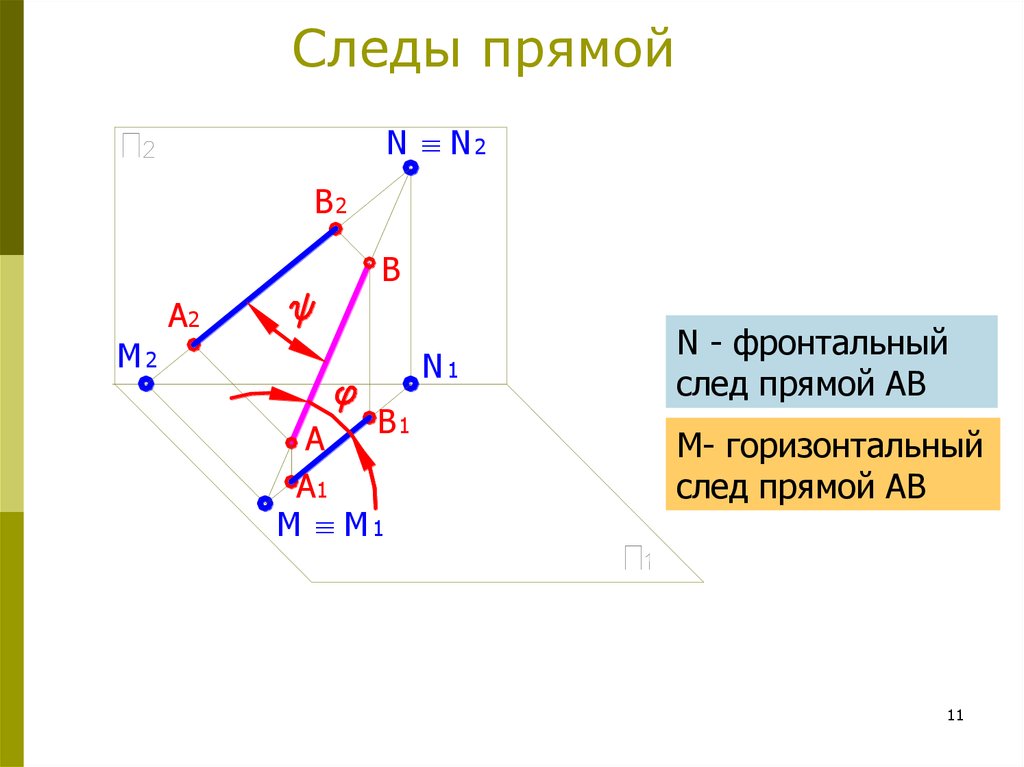
10. Следы прямой
Точки пересечения прямой линии сплоскостями проекции называются следами
прямой.
Точка пересечения прямой с горизонтальной
плоскостью проекций называется
горизонтальным следом прямой.
Точка пересечения прямой с фронтальной
плоскостью проекций называется
фронтальным следом прямой.
10
11. Следы прямой
N N 2B2
B
M 2
A2
N 12
B1
A
A1
M M 1
N - фронтальный
след прямой АВ
М- горизонтальный
след прямой АВ
11
12. Следы прямой
N2B2
N - фронтальный
след прямой АВ
A2
x
M2
B1
A1
M1
N1
М - горизонтальный
след прямой АВ
12
13. Способы задания прямой
1. По координатам точек концов отрезкапрямой (проекциям отрезка прямой).
2. Параметрами отрезка прямой линии:
- натуральной величиной отрезка (НВ);
- углами наклона к плоскостям проекций - ( ₁)
и ( ₂);
- угол между линией отрезка и
горизонтальной плоскостью ( ₁);
- угол между линией отрезка и фронтальной
плоскостью ( ₂).
13
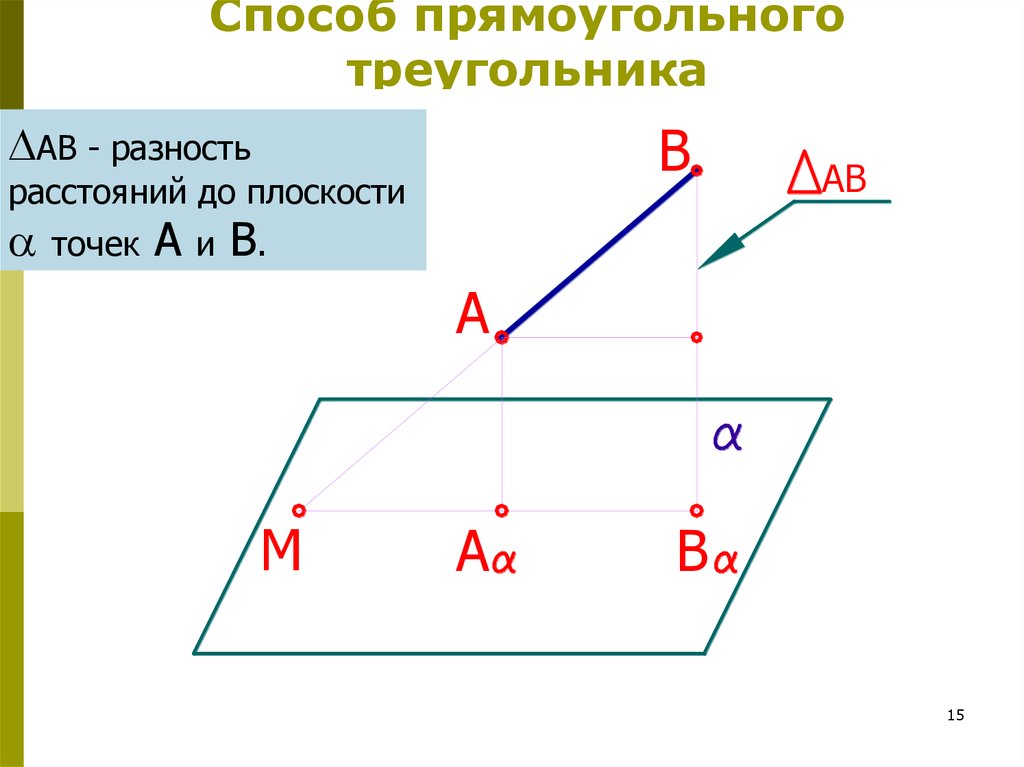
14. Способ прямоугольного треугольника
Натуральная величина отрезка прямойобщего положения равна гипотенузе
прямоугольного треугольника, одним
катетом которого является проекция
отрезка на любую плоскость проекций,
другим – разность расстояний концов
отрезка до той же плоскости проекций.
14
15. Способ прямоугольного треугольника
BАВ - разность
расстояний до плоскости
точек
А
и
B
AB
В.
A
M
A
A
B
15
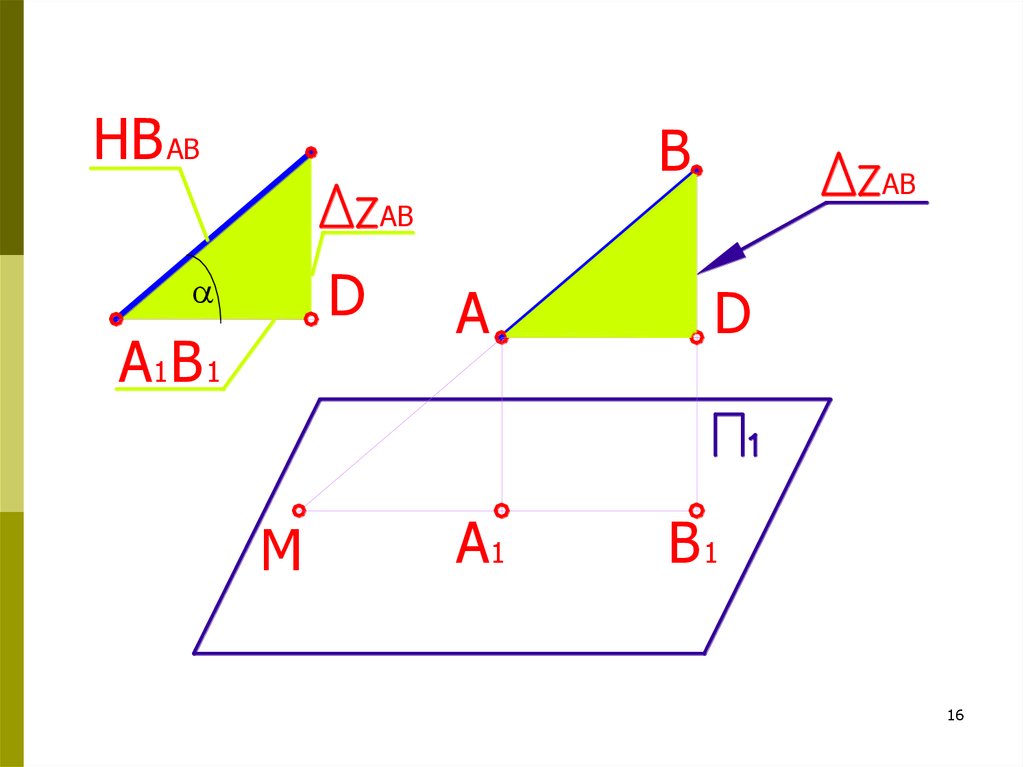
16.
HB ABB
AB
AB
D
A1 B 1
M
A
A1
D
B1
16
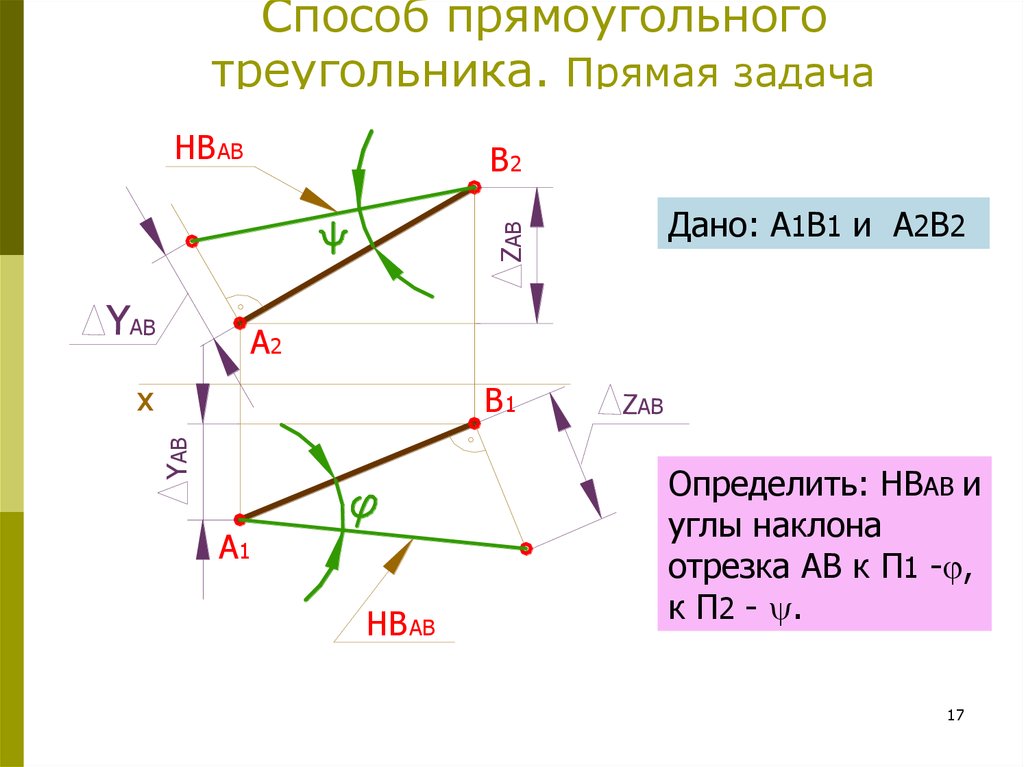
17. Способ прямоугольного треугольника. Прямая задача
HB ABBB22
Z
ZAB
AB
Дано: А1В1 и А2В2
YYABAB A2 AA22
xx
Y
YAB
AB
BB11
A1
AA11
HB
HBAB
AB
ZZAB
AB
Определить: НВАВ и
углы наклона
отрезка АВ к П1 - ,
к П2 - .
17
18. Способ прямоугольного треугольника. Обратная задача
Дано: НВАВ,1 1
R=
=30, =45 .
0
ZAB= 5
A1
B
AB
А(40,50,5)
1
A
A 2B 2
B
YAB
ZAB
ХА<ХВ, YA>YB,
B2
A2
x
ZA<ZB.
0
B1
YAB
Построить проекции
отрезка АВ.
A1
18
19. ВЫВОДЫ
По положению относительно плоскостейпроекций различают:
- прямые общего положения (непараллельные
и неперпендикулярные плоскостям
проекций),
- прямые частного положения: параллельные
или перпендикулярные плоскостям
проекций.
19
20. ВЫВОДЫ
Проекции прямых частного положениядают ответы на вопросы позиционных и
метрических задач.
Способ прямоугольного треугольника
поясняет связи между натуральной
величиной отрезка, его проекциями и
углами наклона к плоскостям проекций.
20
21. Контрольные вопросы
1.2.
Как по заданным проекциям
отрезка определить его
натуральную величину?
Как по заданным проекциям
отрезка определить углы наклона
его к плоскостям проекций?
21
22. Контрольные вопросы
3.Какое положение прямой дает
проекцию отрезка этой прямой,
равную натуральной величине?
4.
Что такое «след прямой»?
Как его построить?
5.
22











 drafting
drafting








