Similar presentations:
Способ прямоугольного треугольника. Плоскости
1. Лекция 3 Способ прямоугольного треугольника. Плоскости
ЛЕКЦИЯ 3Способ прямоугольного
треугольника.
Плоскости
1.
Способ прямоугольного треугольника
2.
Задание плоскости
3.
Следы плоскости
4.
Плоскости общего и частного положения
5.
Особые линии плоскости
2. Способы задания прямой
СПОСОБЫ ЗАДАНИЯ ПРЯМОЙ1. По координатам точек концов отрезка прямой (проекциям
отрезка прямой) - А(x,y,z) и В (x,y,z)
2. Параметрами отрезка прямой линии:
- натуральной величиной отрезка (НВ)
- углами наклона к плоскостям проекций - (П₁) и ψ (П₂):
- угол между линией отрезка и горизонтальной
плоскостью (П₁)
ψ- угол между линией отрезка и фронтальной плоскостью
(П₂)
2
3. Способ прямоугольного треугольника
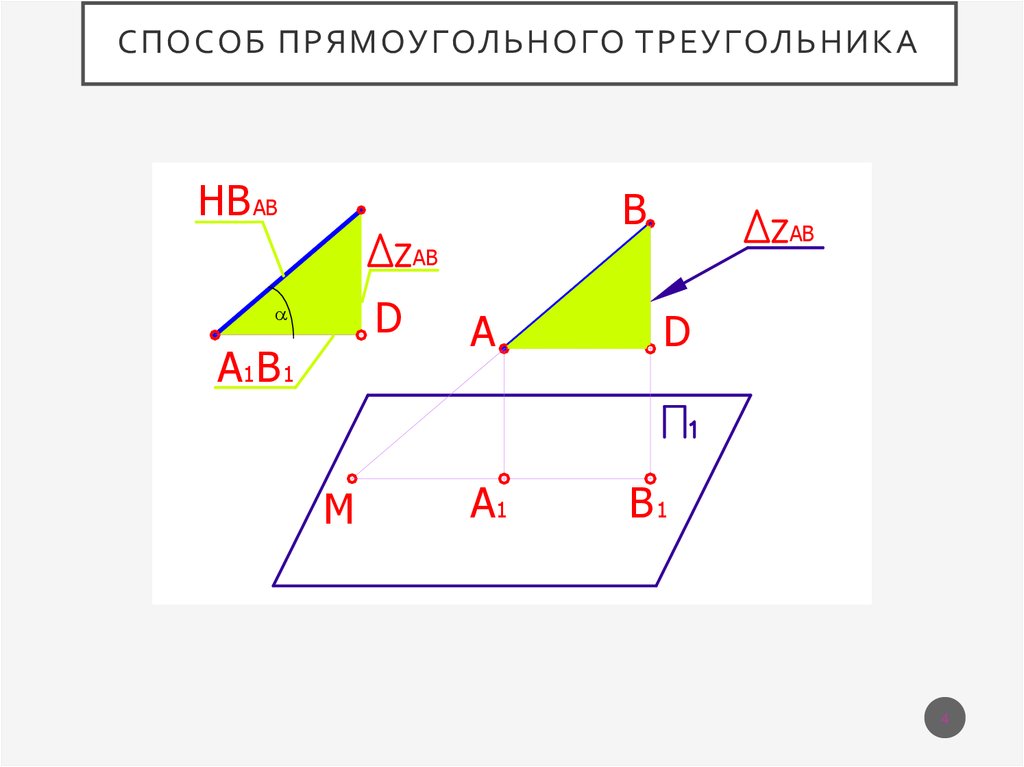
СПОСОБ ПРЯМОУГОЛЬНОГОТРЕУГОЛЬНИКА
Натуральная величина отрезка прямой общего
положения равна гипотенузе прямоугольного
треугольника,
одним катетом которого является проекция отрезка на
любую плоскость проекций,
другим – разность расстояний концов отрезка до той же
плоскости проекций
3
4. Способ прямоугольного треугольника
СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАHB AB
B
AB
AB
D
A1 B 1
M
A
A1
D
B1
4
5. Способ прямоугольного треугольника. Прямая задача
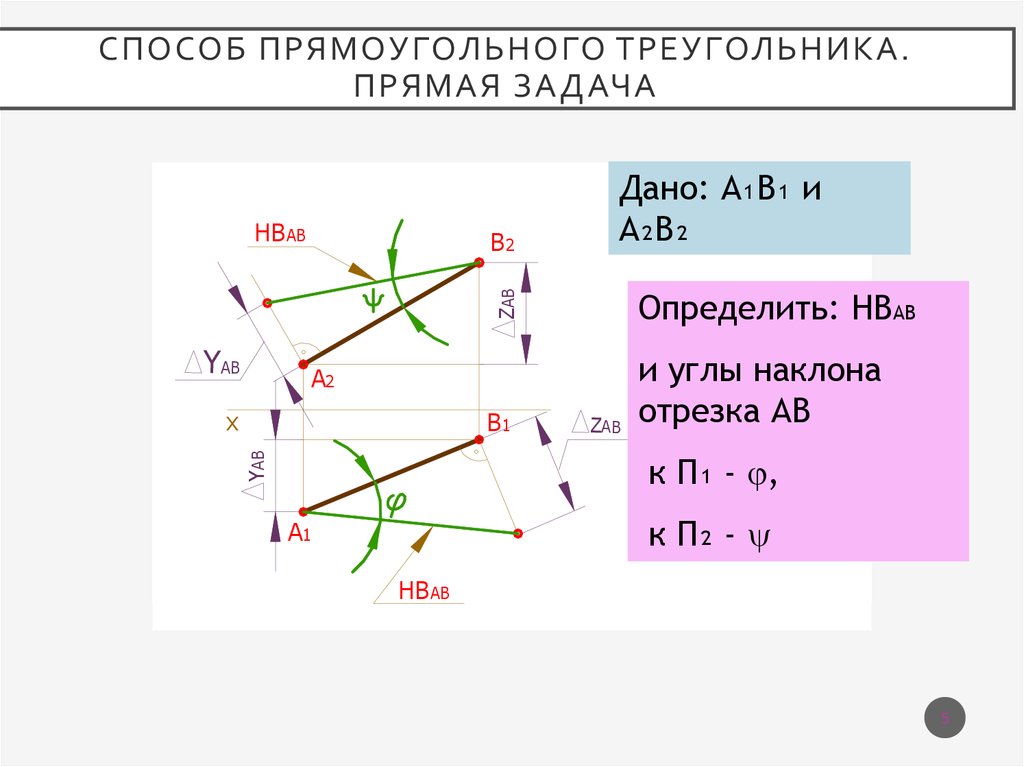
СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.ПРЯМАЯ ЗАДАЧА
B2
B2
ZABZAB
HB AB
YAB
YAB
A2 A2
A2
YABYAB
x
x
Дано: А₁В₁ и
А₂В₂
B1
B1
Определить: НВАВ
ZAB
ZAB
и углы наклона
отрезка АВ
к П₁ - ,
A1
A1
A1
HB AB
HB AB
к П₂ -
5
6. Вопрос 1
ВОПРОС 1Дано:
А1В1 иА2В2 – проекции прямой общего
положения
Дополнить фразу:
Для определения ψ и ϕ нужно ... .
7. Способ прямоугольного треугольника. Обратная задача
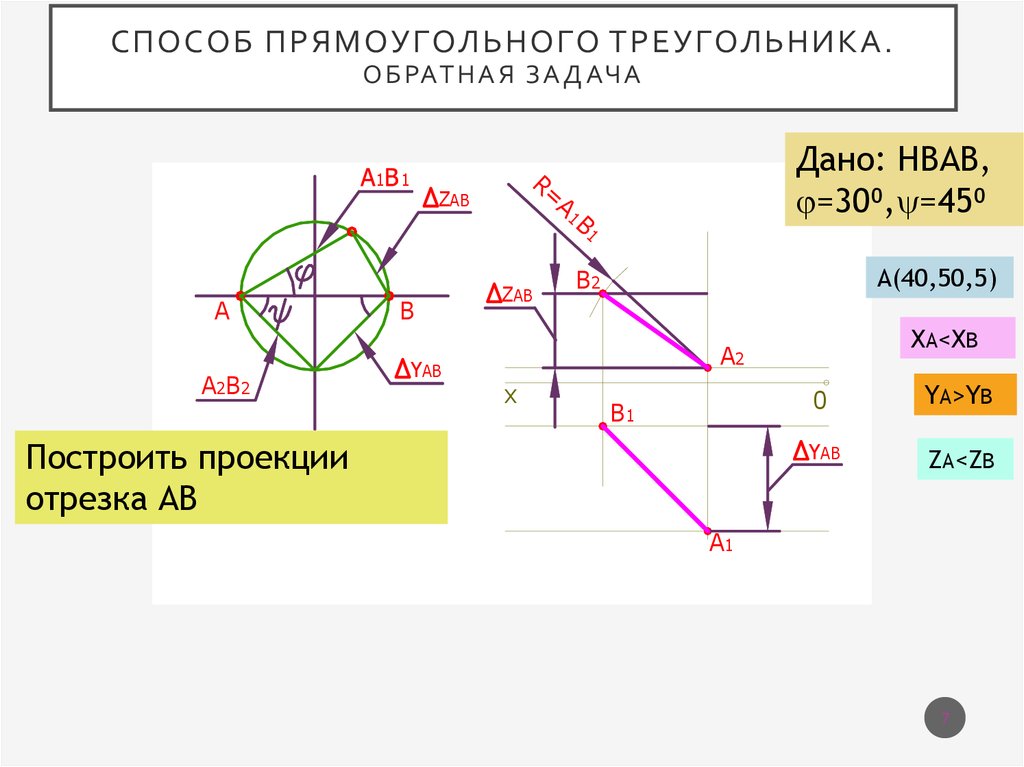
СПОСОБ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.О Б РАТ Н А Я З А Д АЧ А
1
A
A 2B 2
Дано: НВАВ,
=30⁰, =45⁰
R
ZAB= 50 =A
1B
AB
1
1
B
YAB
ZAB
А(40,50,5)
B2
ХА<ХВ
A2
x
B1
Построить проекции
отрезка АВ
0
YA>YB
YAB
ZA<ZB
A1
7
8. Вопрос 2
ВОПРОС 2Завершить фразу:
Диаметр круговой диаграммы равен ... .
9. Следы плоскости – линии пересечения заданной плоскости с плоскостями проекций
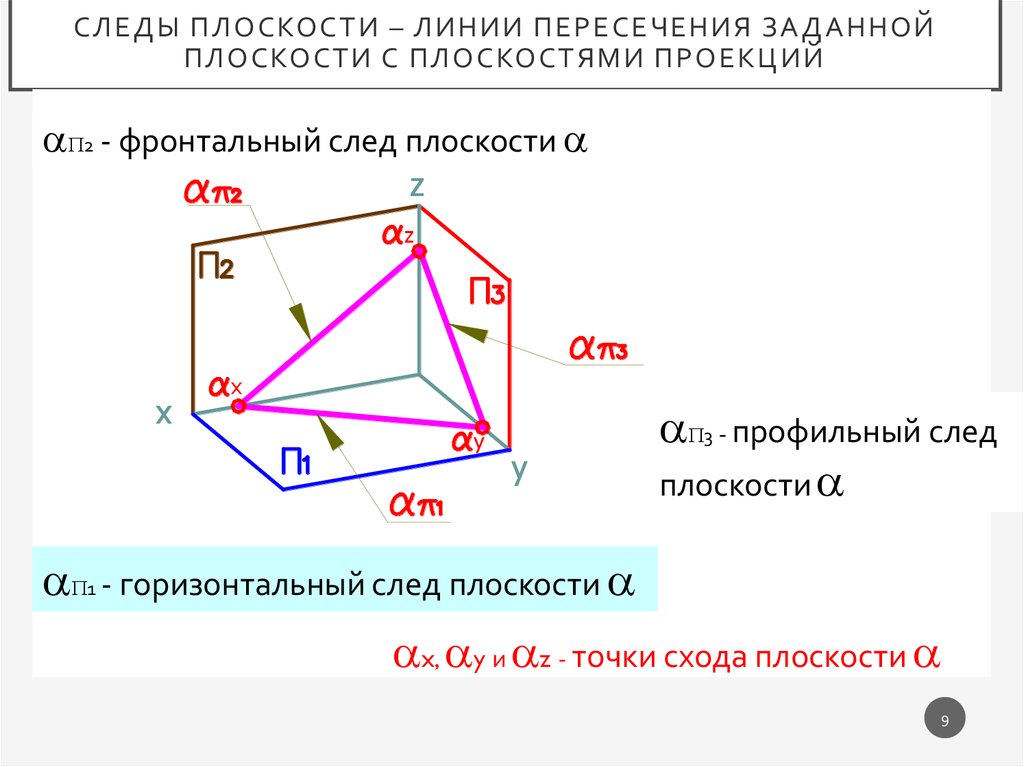
СЛ Е Д Ы ПЛ О СКО СТ И – Л ИНИИ ПЕ Р Е СЕ ЧЕ НИЯ З А Д А ННО ЙПЛ О СКО СТИ С ПЛ ОСКОСТЯМИ ПРОЕКЦ ИЙ
2 - фронтальный след плоскости
z
z
x
x
y
y
3 - профильный след
плоскости
1 - горизонтальный след плоскости
x, y и z - точки схода плоскости
9
10. Следы плоскости
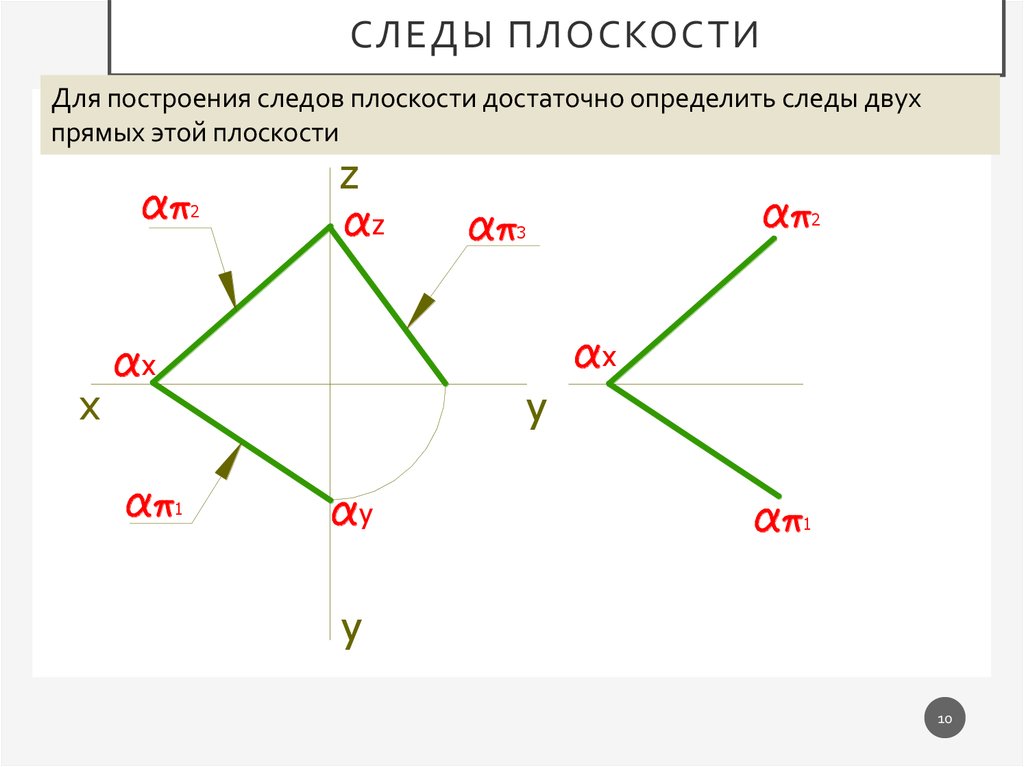
СЛЕДЫ ПЛОСКОСТИДля построения следов плоскости достаточно определить следы двух
прямых этой плоскости
z
2
x
z
2
3
x
x
y
1
y
1
y
10
11. Плоскости общего положения
ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯПлоскости общего положения - это плоскости,
неперпендикулярные и непараллельные плоскостям
проекций
Плоскости общего положения не проецируются в
натуральную величину
11
12. Плоскости частного положения
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ• Плоскости параллельные
плоскостям проекций
• Плоскости перпендикулярные
плоскостям проекций
12
13. Плоскости параллельные плоскостям проекций
ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
A
B
C
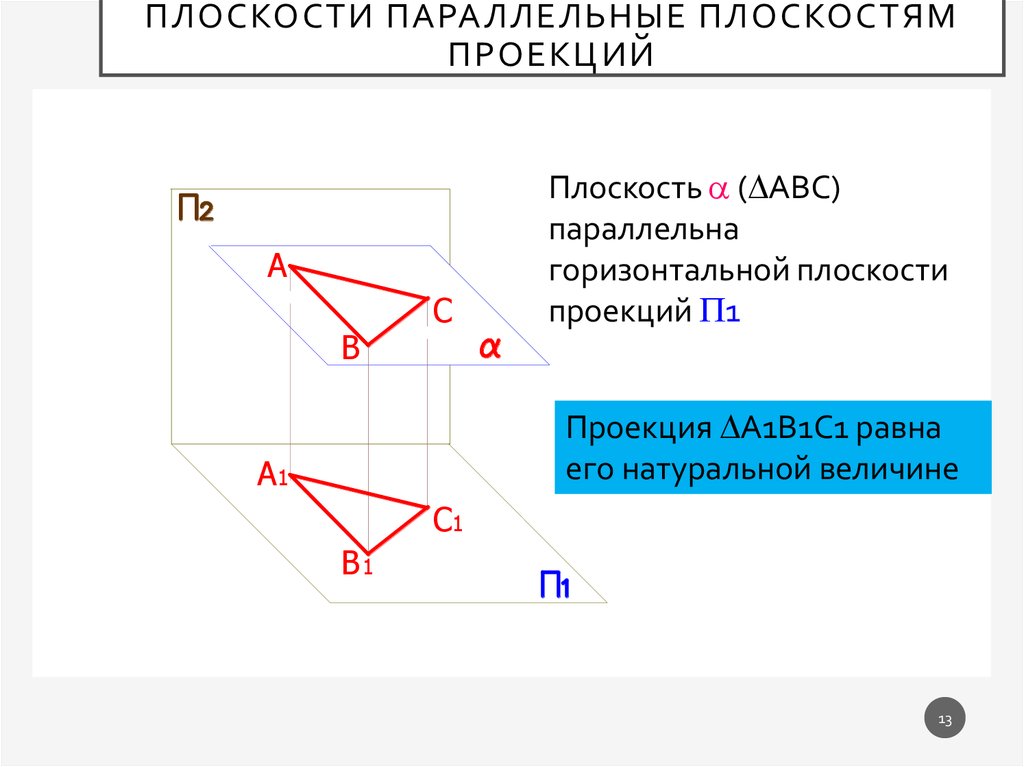
Плоскость ( АВС)
параллельна
горизонтальной плоскости
проекций 1
Проекция А1В1С1 равна
его натуральной величине
A1
C1
B1
13
14. Плоскости параллельные плоскостям проекций
ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
Плоскость АВС параллельна 1 - горизонтальная
плоскость
АА22 А2
ВВ22 В 2
СС22С2
Z = соnst
x
xxx
x
ВВ11 В 1
АА11
А1
НВ
НВABC
ABC
С1
СС11
14
15. Плоскости параллельные плоскостям проекций
ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
B2
B2
A2
A2
HB ABC
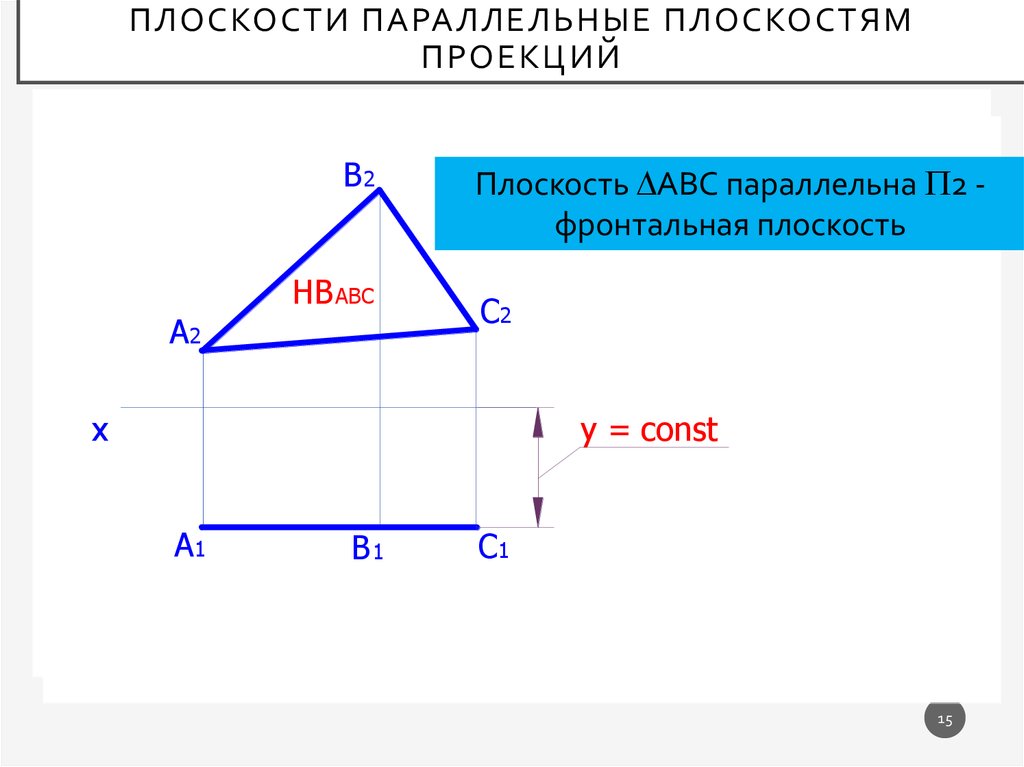
Плоскость АВС параллельна 2 фронтальная плоскость
C2
C2
x
x
y = const
A1
A1
B1
B1
C1
C1
15
16. Плоскости параллельные плоскостям проекций
ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТЯМ ПРОЕКЦИЙx=const
B2
A2
C2
B3
AA33
HB ABC
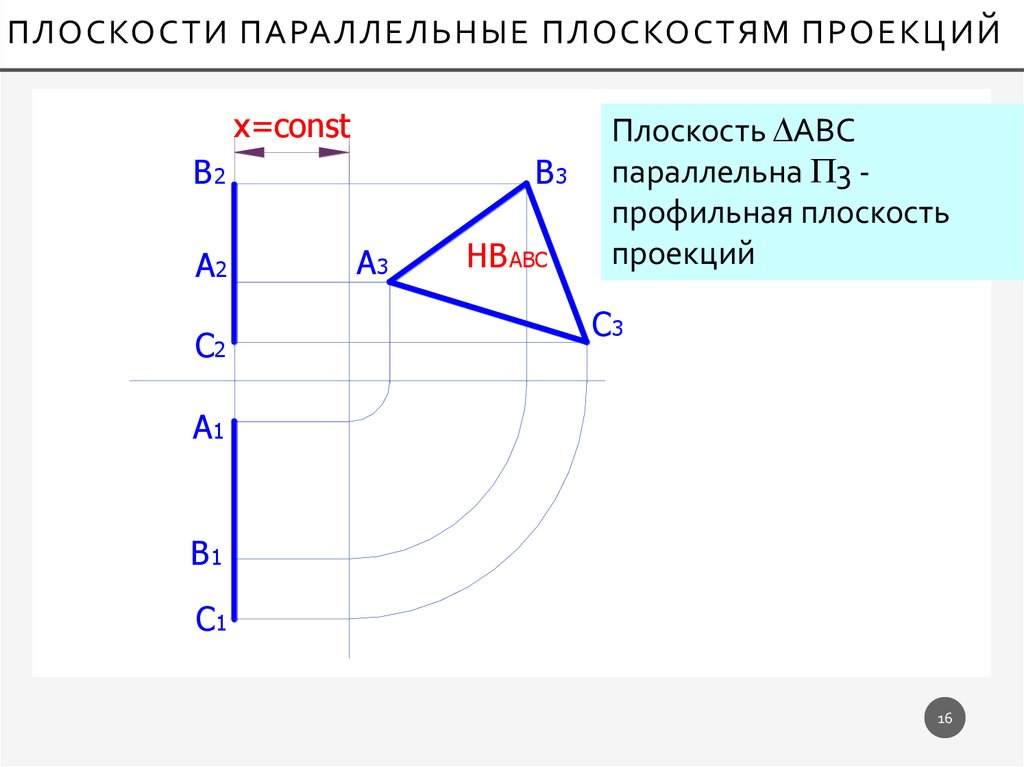
Плоскость АВС
параллельна 3 профильная плоскость
проекций
C3
A1
B1
C1
16
17. Плоскости перпендикулярные плоскостям проекций
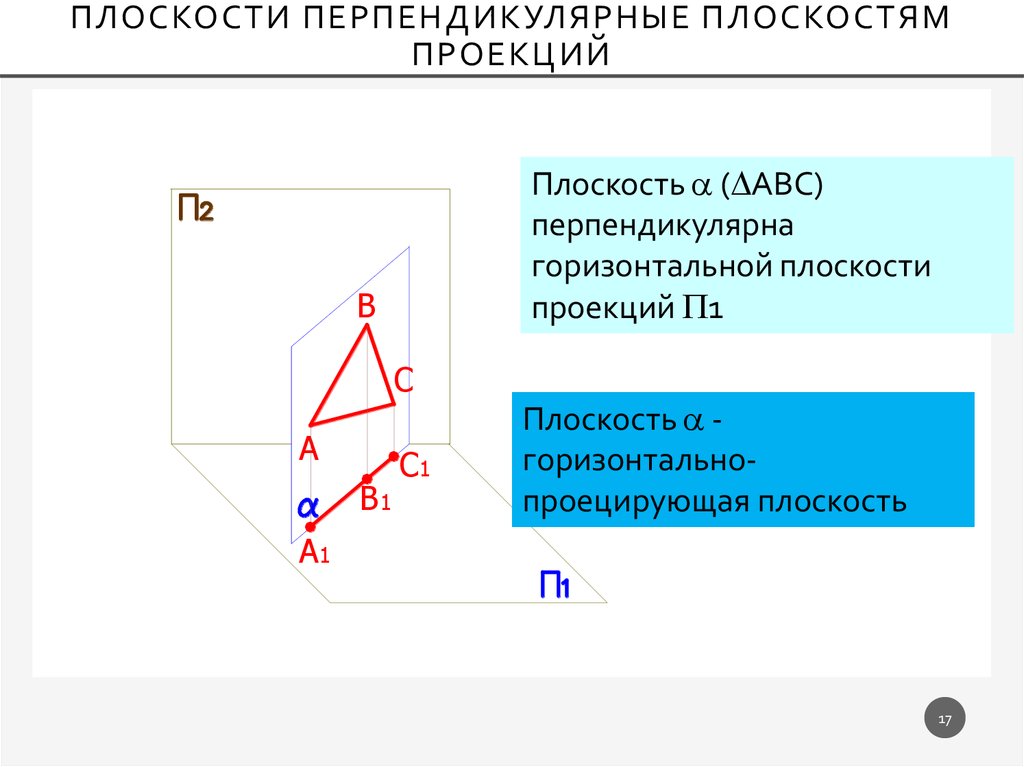
ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
Плоскость ( АВС)
перпендикулярна
горизонтальной плоскости
проекций 1
B
C
A
B1
C1
Плоскость горизонтальнопроецирующая плоскость
A1
17
18. Плоскости перпендикулярные плоскостям проекций
ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
2
C2
A2
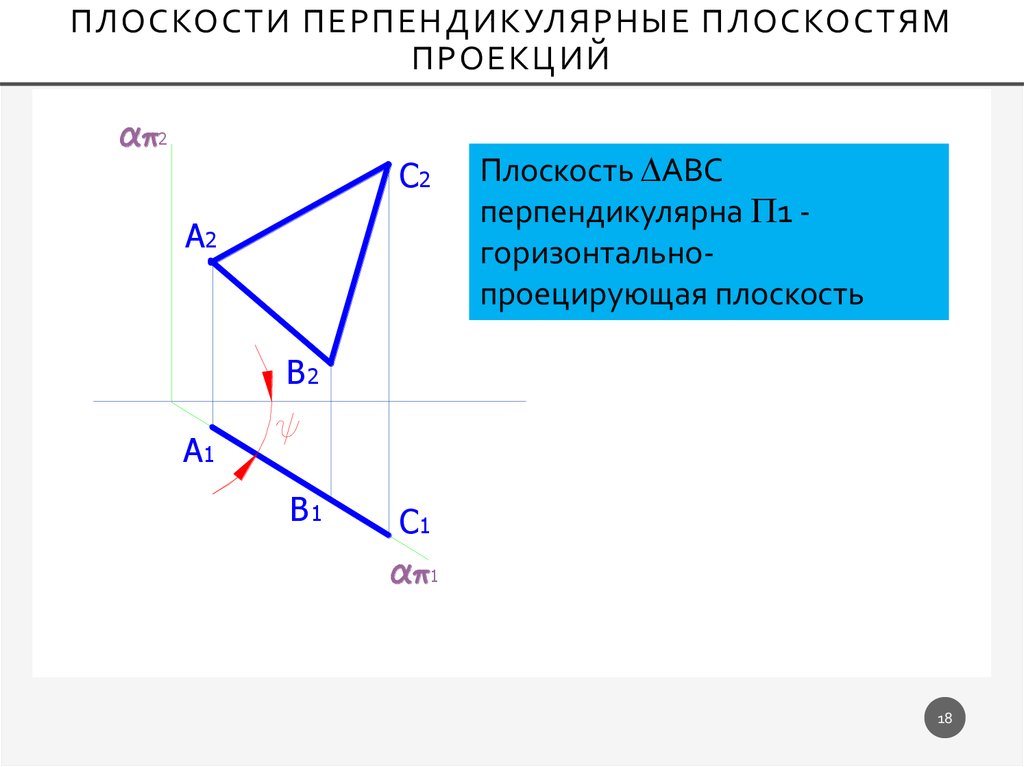
Плоскость АВС
перпендикулярна 1 горизонтальнопроецирующая плоскость
B2
A1
B1
C1
1
18
19. Плоскости перпендикулярные плоскостям проекций
ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
C2
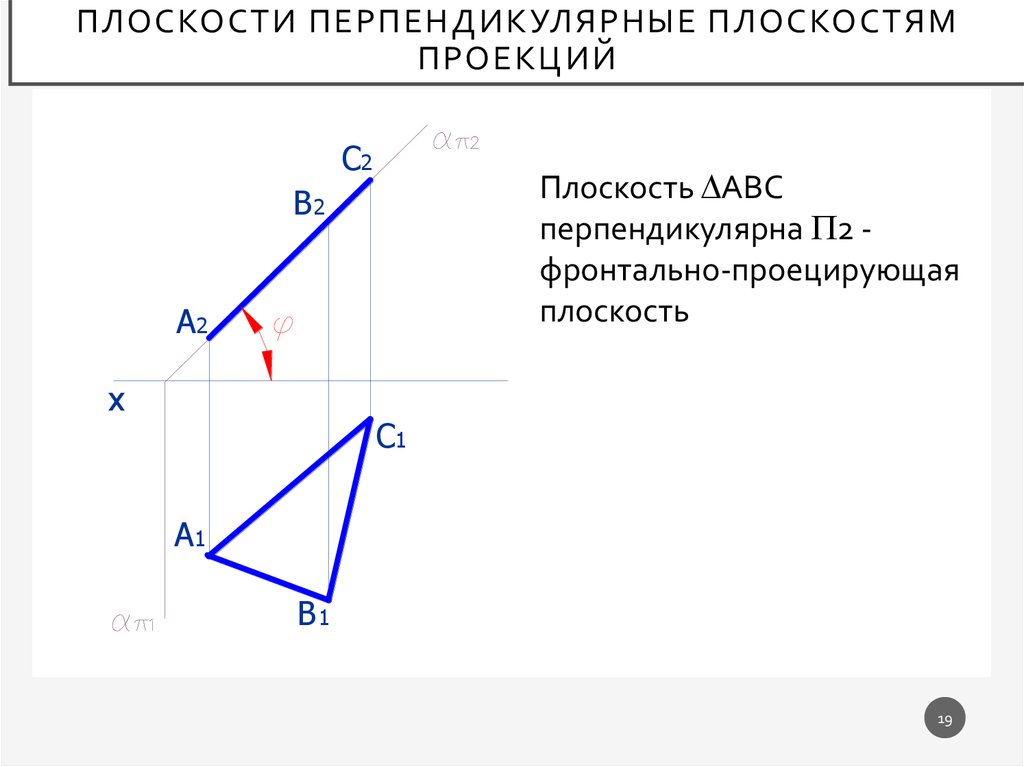
Плоскость АВС
перпендикулярна 2 фронтально-проецирующая
плоскость
B2
A2
x
C1
A1
B1
19
20. Плоскости перпендикулярные плоскостям проекций
ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТЯМПРОЕКЦИЙ
z
A3
A2
B3
B2
C2
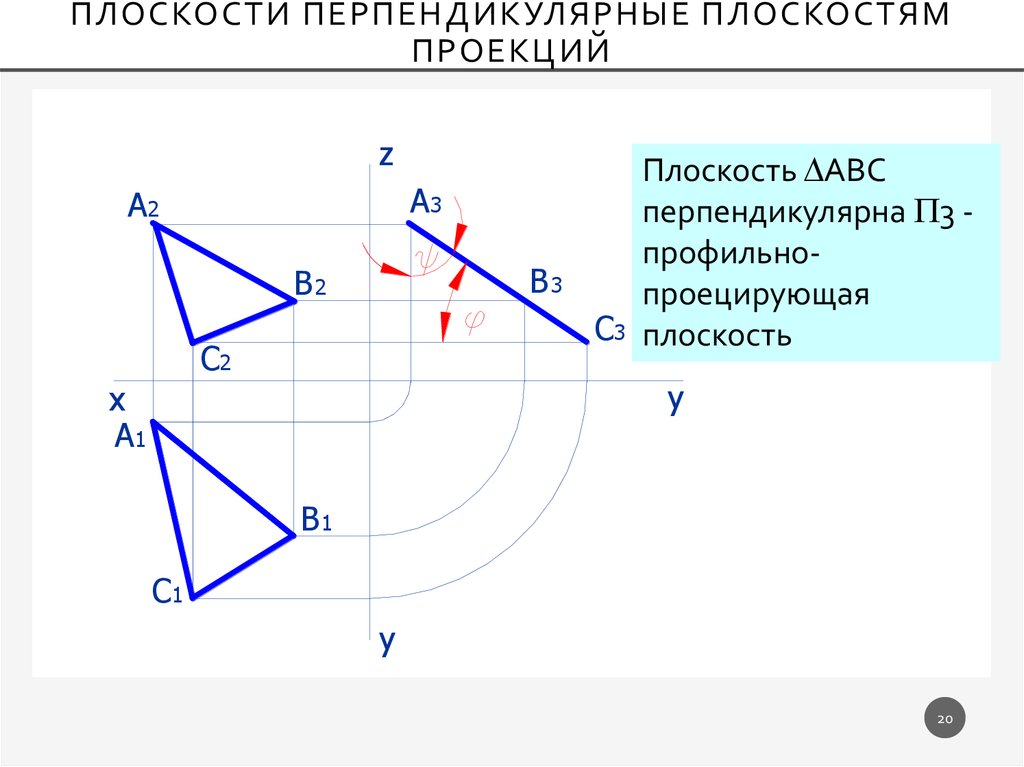
Плоскость АВС
перпендикулярна 3 профильнопроецирующая
C3 плоскость
y
x
A1
B1
C1
y
20
21. Вопрос 3
ВОПРОС 3Вырожденную проекцию имеют плоскости:
1. Уровня
2. Проецирующие
3. Общего положения
4. Все
22. Особые линии плоскости. Горизонталь плоскости
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ГОРИЗОНТАЛЬ ПЛОСКОСТИ
• Горизонталь плоскости - прямая
принадлежащая заданной плоскости и
параллельная плоскости проекций
• Если плоскость задана следами, то
горизонтальный след плоскости нулевая горизонталь этой плоскости
22
23. Особые линии плоскости. Фронталь плоскости
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ФРОНТАЛЬ ПЛОСКОСТИ
• Фронталь плоскости - прямая
принадлежащая плоскости и
параллельная плоскости проекций
• Если плоскость задана следами, то
фронтальный след плоскости - нулевая
фронталь этой плоскости
23
24. Особые линии плоскости. Горизонталь плоскости
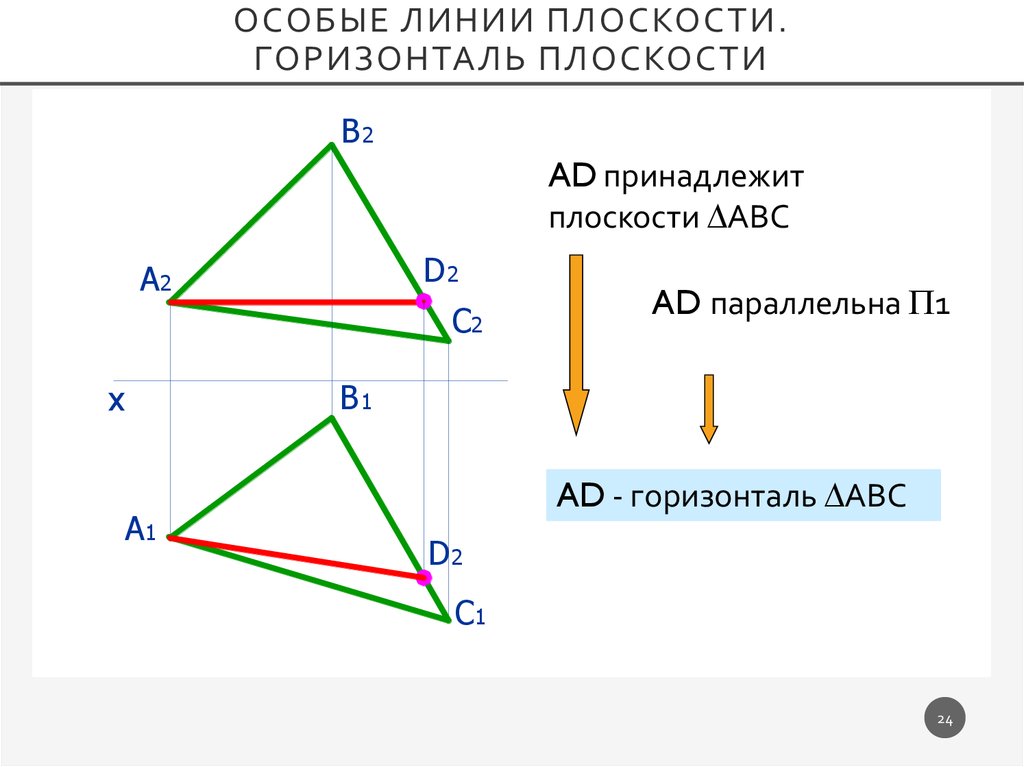
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ГОРИЗОНТАЛЬ ПЛОСКОСТИ
B2
AD принадлежит
плоскости АВС
D2
A2
C2
AD параллельна 1
B1
x
A1
AD - горизонталь АВС
D2
C1
24
25. Особые линии плоскости. Фронталь плоскости
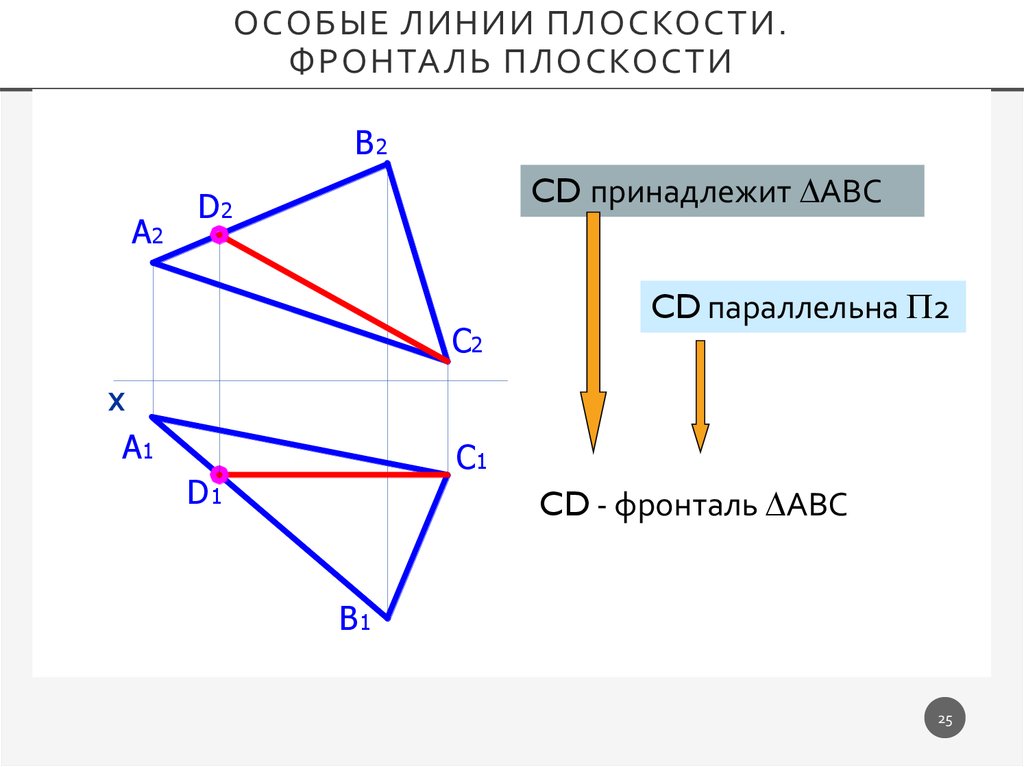
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ФРОНТАЛЬ ПЛОСКОСТИ
B2
A2
CD принадлежит АВС
D2
C2
x
A1
CD параллельна 2
C1
D1
CD - фронталь АВС
B1
25
26. Особые линии плоскости
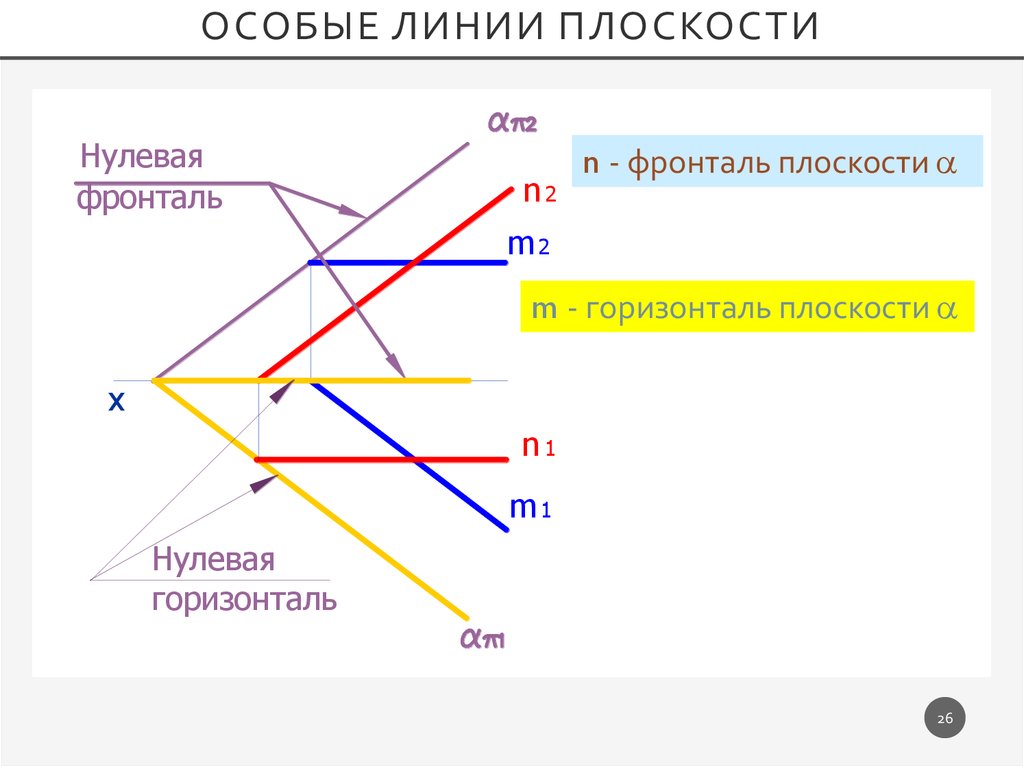
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИНулевая
фронталь
n2
n - фронталь плоскости
m2
m - горизонталь плоскости
x
n1
m1
Нулевая
горизонталь
26
27. Вопрос 4
ВОПРОС 4Построение проекций горизонтали
плоскости следует начинать с плоскости
1. П1
2. П2
3. П3
4. Оси х
28. Особые линии плоскости. Линии наибольшего наклона плоскости
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
Линии наибольшего наклона заданной плоскости к
плоскости проекций - линии принадлежащие
плоскости и перпендикулярные горизонтали и
фронтали плоскости :
1.Линия наибольшего наклона плоскости к
горизонтальной плоскости проекций называется
линией ската
2.Линия наибольшего наклона плоскости к
горизонтальной или профильной плоскости
проекций не имеет другого названия
28
29. Особые линии плоскости. Линии наибольшего наклона плоскости
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
Линии наибольшего наклона заданной плоскости к
плоскости проекций – линии, принадлежащие плоскости
и перпендикулярные горизонтали и фронтали плоскости :
1. Линия наибольшего наклона плоскости к
горизонтальной плоскости проекций называется
линией ската
2. Линия наибольшего наклона плоскости к
фронтальной плоскости проекций не имеет другого
названия
29
30. Особые линии плоскости. Линия ската
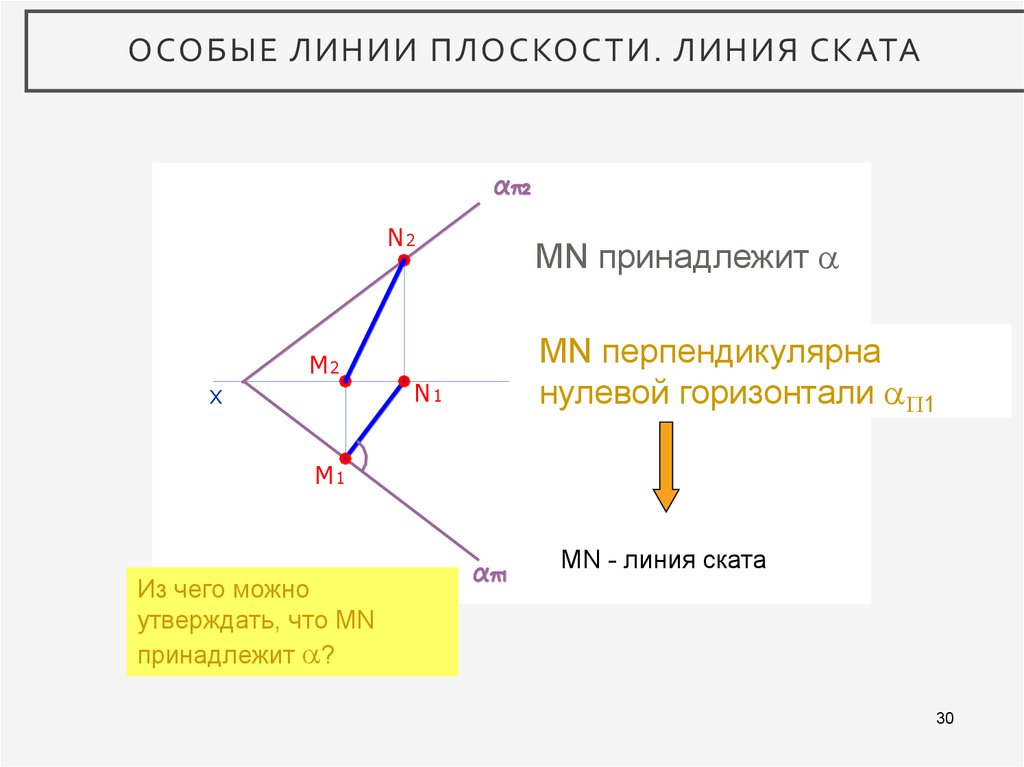
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ. ЛИНИЯ СКАТАN2
M2
x
N1
MN принадлежит
MN перпендикулярна
нулевой горизонтали 1
M1
MN - линия ската
Из чего можно
утверждать, что MN
принадлежит ?
30
31. Линия наибольшего наклона плоскости
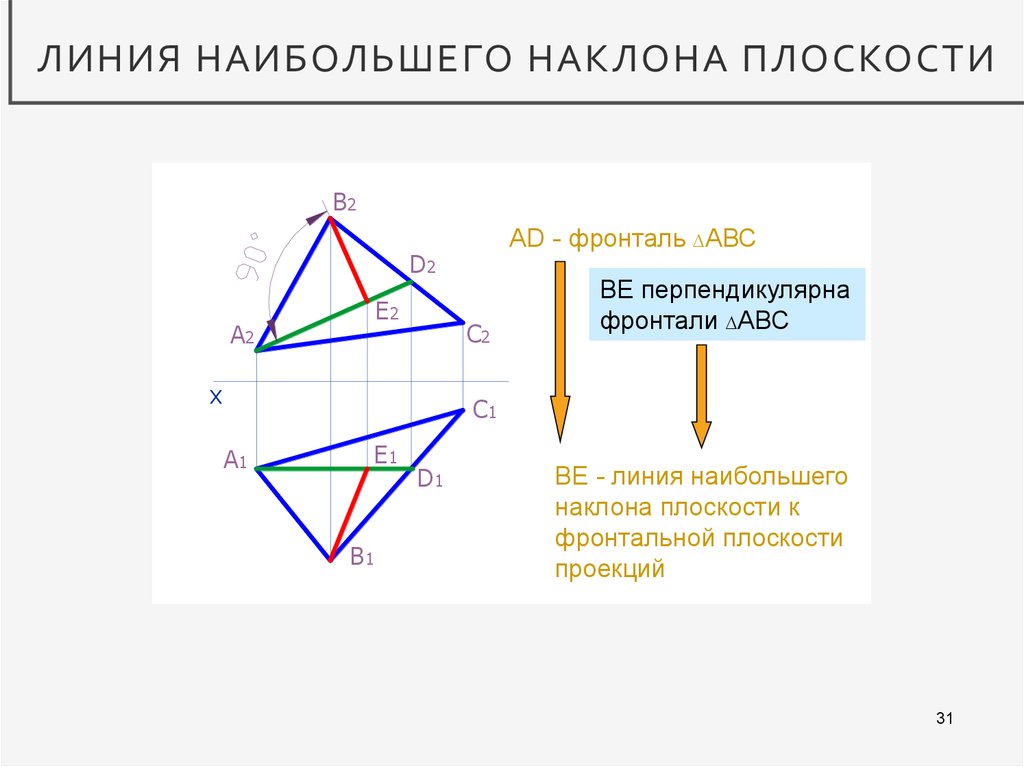
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИB2
AD - фронталь АВС
D2
E2
A2
C2
x
ВЕ перпендикулярна
фронтали АВС
C1
A1
E1
B1
D1
ВЕ - линия наибольшего
наклона плоскости к
фронтальной плоскости
проекций
31
32. Вопрос 5
ВОПРОС 5Построение линии ската плоскости следует
начинать с
1. Горизонтали
2. Фронтали
3. Следов
4. Профильной проекции
33. ВЫВОДЫ
• Особые линии плоскости позволяют решать позиционныезадачи для заданной плоскости
• Особые линии плоскости, принадлежащие ей:
• горизонталь
• фронталь
• линия ската
• линии наибольшего наклона плоскости
Особая линия плоскости, имеющая одну общую точку с
плоскостью - нормаль плоскости
33
34. Плоскость. Позиционные и метрические задачи
ПЛОСКОСТЬ.ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ
• Прямая может
• принадлежать плоскости
• пересекать плоскость под некоторым углом
• пересекать плоскость под прямым углом (быть
перпендикулярна плоскости)
• быть параллельна плоскости
34
35. Особые линии плоскости. Нормаль
ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ. НОРМАЛЬ• Нормаль - прямая перпендикулярная плоскости.
(не принадлежит плоскости, имеет с ней одну общую точку).
• Прямая перпендикулярна плоскости, если она перпендикулярна двум
пересекающимся прямым этой плоскости.
• За эти две прямые, лежащие в одной плоскости, принимают горизонталь и
фронталь плоскости, т.к. к ним можно провести линию под прямым углом.
35
36. Нормаль
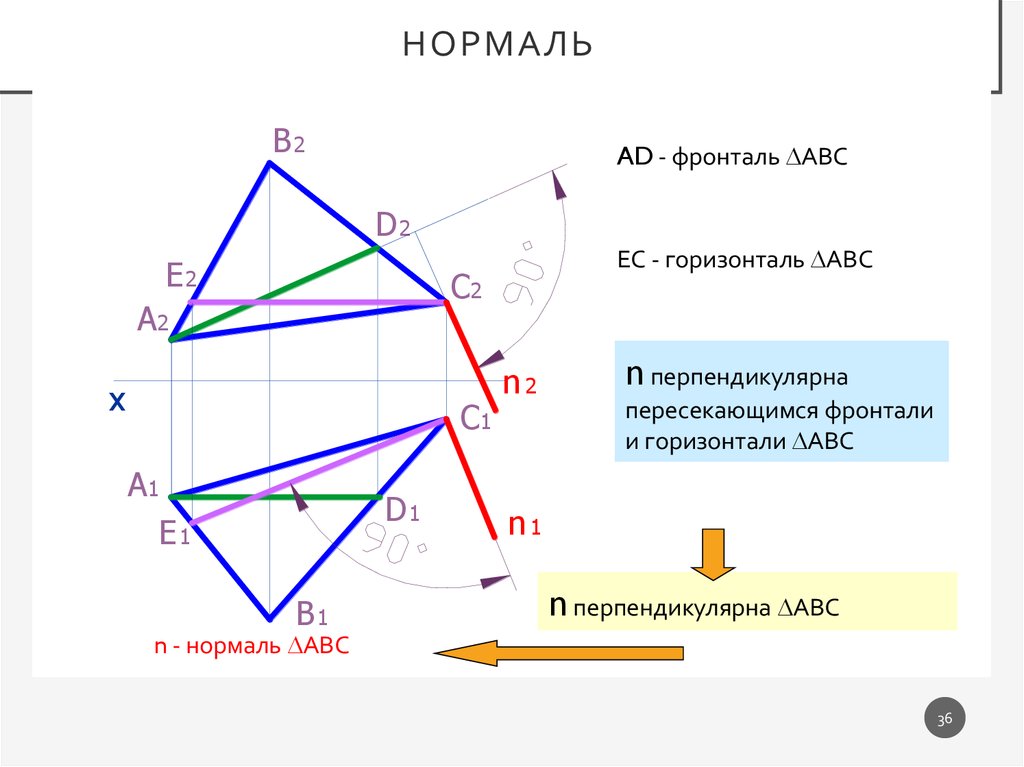
НОРМАЛЬB2
AD - фронталь АВС
B2
D2
E2
ЕС - горизонталь АВС
C2
C 2 C2
AA2 2
xx
C1 C1
AA1 1
E1
D1
B1
B1
n2
n перпендикулярна
пересекающимся фронтали
и горизонтали АВС
n1
n перпендикулярна АВС
n - нормаль АВС
36
37. Нормаль
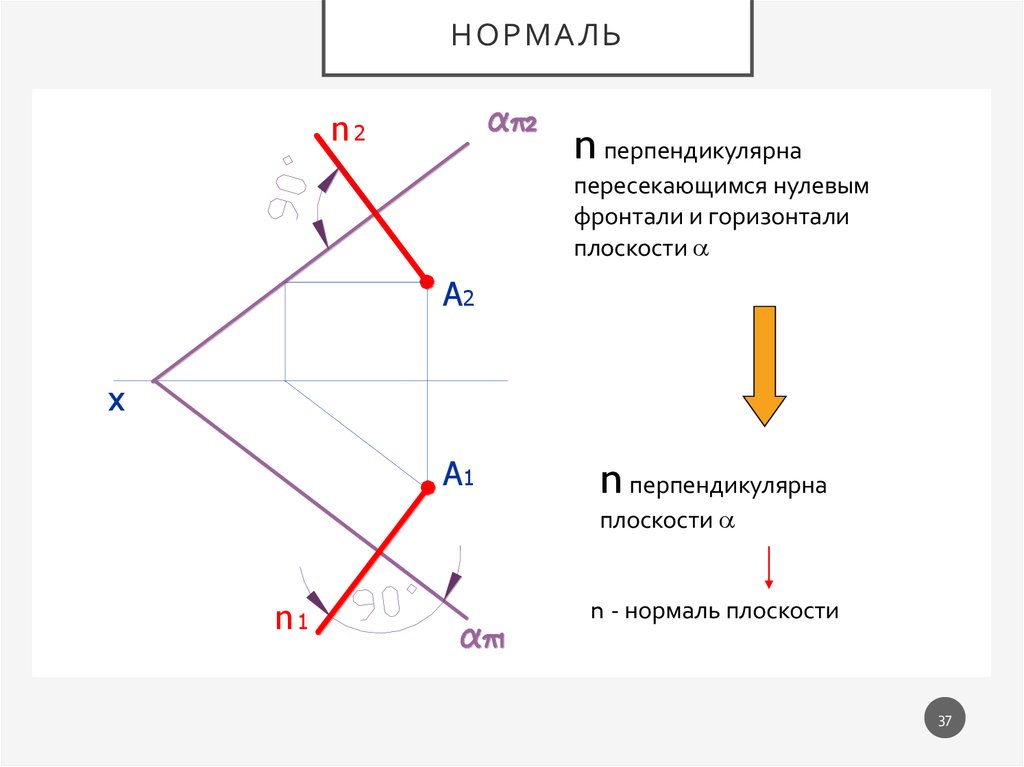
НОРМАЛЬn2
n перпендикулярна
пересекающимся нулевым
фронтали и горизонтали
плоскости
A2
x
A1
n перпендикулярна
плоскости
n1
n - нормаль плоскости
37
38. Построение проекций плоской фигуры по особым линиям плоскости
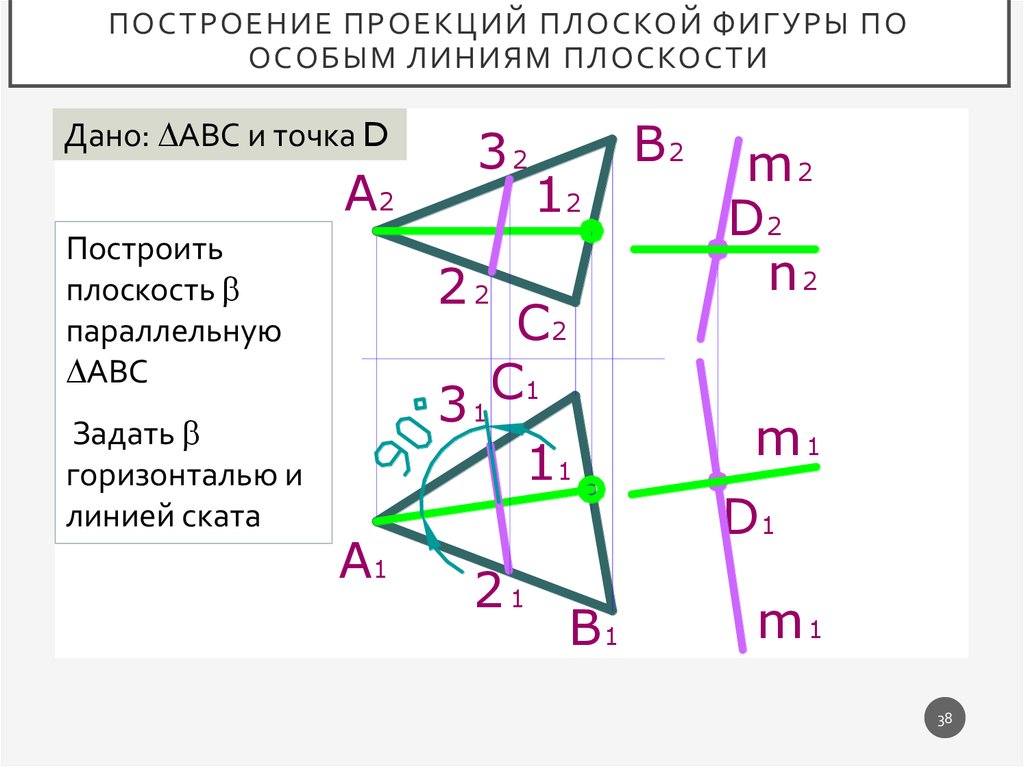
ПОСТРОЕНИЕ ПРОЕКЦИЙ ПЛОСКОЙ ФИГУРЫ ПООСОБЫМ ЛИНИЯМ ПЛОСКОСТИ
Дано: АВС и точка D
Построить
плоскость
параллельную
АВС
Задать
горизонталью и
линией ската
A22
A
32
12
2
BB
2
22
CC2 2
CC1 1
31
A
A11
11
2 1 B1
B1
m2
D2
n2
m1
D1
m1
38
39. Построение проекций плоской фигуры по особым линиям плоскости
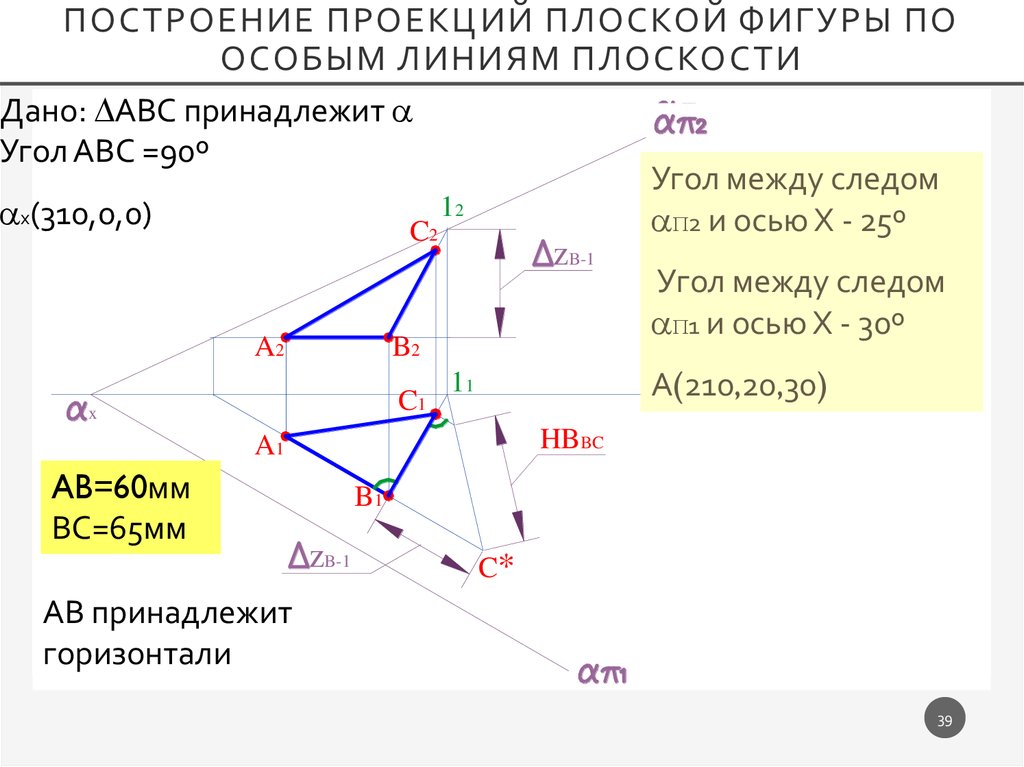
ПОСТРОЕНИЕ ПРОЕКЦИЙ ПЛОСКОЙ ФИГУРЫ ПООСОБЫМ ЛИНИЯМ ПЛОСКОСТИ
Дано: АВС принадлежит
Угол АВС =90º
Угол между следом
1
2
12
x(310,0,0)
C
2
2 и осью Х - 25º
C2
zzB-1
B-1
Угол между следом
1 и осью Х - 30º
A2
B2
A2
x
x
B2
11
C
1 11
C1
А(210,20,30)
HB
HBBC
BC
A
A11
AB=60мм
ВС=65мм
B
BB11 1
zzB-1
B-1
C
C*
*
АВ принадлежит
горизонтали
39
40. Построение проекций плоской фигуры по особым линиям плоскости
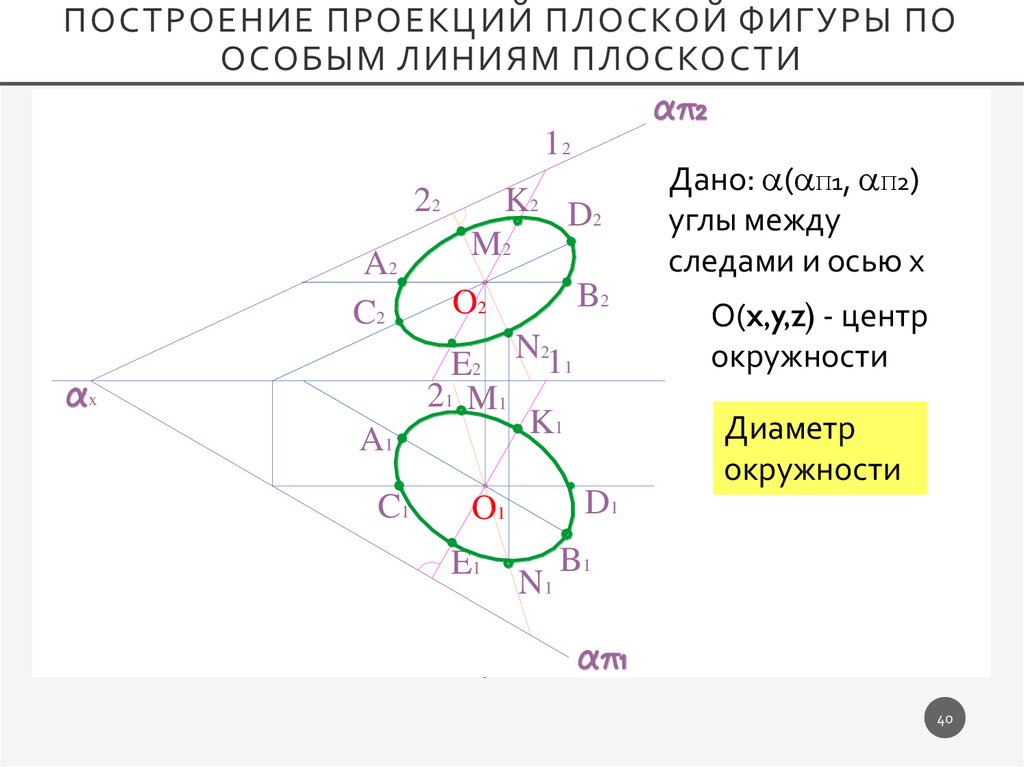
ПОСТРОЕНИЕ ПРОЕКЦИЙ ПЛОСКОЙ ФИГУРЫ ПООСОБЫМ ЛИНИЯМ ПЛОСКОСТИ
YO-2
x
12
Дано: ( 1, 2)
углы между
следами и осью х
22 M2K2 D2
2*
M2
A2
B2
O2
C2
О(x,y,z) - центр
N
2
zO-1окружности
N
2
1
1
E2
21 M1
K1
Диаметр
A1
1* окружности
D1 1*
D1
C1
O1
R
B1
E1
N1
40
41. ВЫВОДЫ
1.Особые линии плоскости позволяют решать
позиционные задачи для заданной плоскости.
2.
Особые линии плоскости, принадлежащие ей:
- горизонталь;
- фронталь;
- линия ската;
- линии наибольшего наклона плоскости.
3.
Особая линия плоскости, не принадлежащая ей нормаль плоскости.
41



















 drafting
drafting








