Ортогональные проекции плоскости. Относительное положение плоскостей

1. Институт фундаментального образования Кафедра “Инженерная графика”

Раздел: Начертательная геометрия
Тема 3.
Ортогональные
проекции плоскости.
Относительное
положение плоскостей
Лектор: Стриганова Лариса Юрьевна
доцент кафедры ИГ
Лекция 3. Ортогональные
проекции плоскости
1

2. Цель и задачи занятия

• Определить графические способы
задания плоскости на эпюре
• Рассмотреть особенности плоскостей
общего и частного положений в
пространстве и на ортогональном
чертеже
Лекция 3. Ортогональные
проекции плоскости
2

3. В результате изучения темы Вы будете знать:

• Способы задания плоскости
• Понятие «Следы плоскости»
• Классификацию плоскостей общего и
частного положений
• Особые линии плоскости
• Относительное положение прямой и
плоскости
• Относительное положение плоскостей
Лекция 3. Ортогональные
проекции плоскости
3

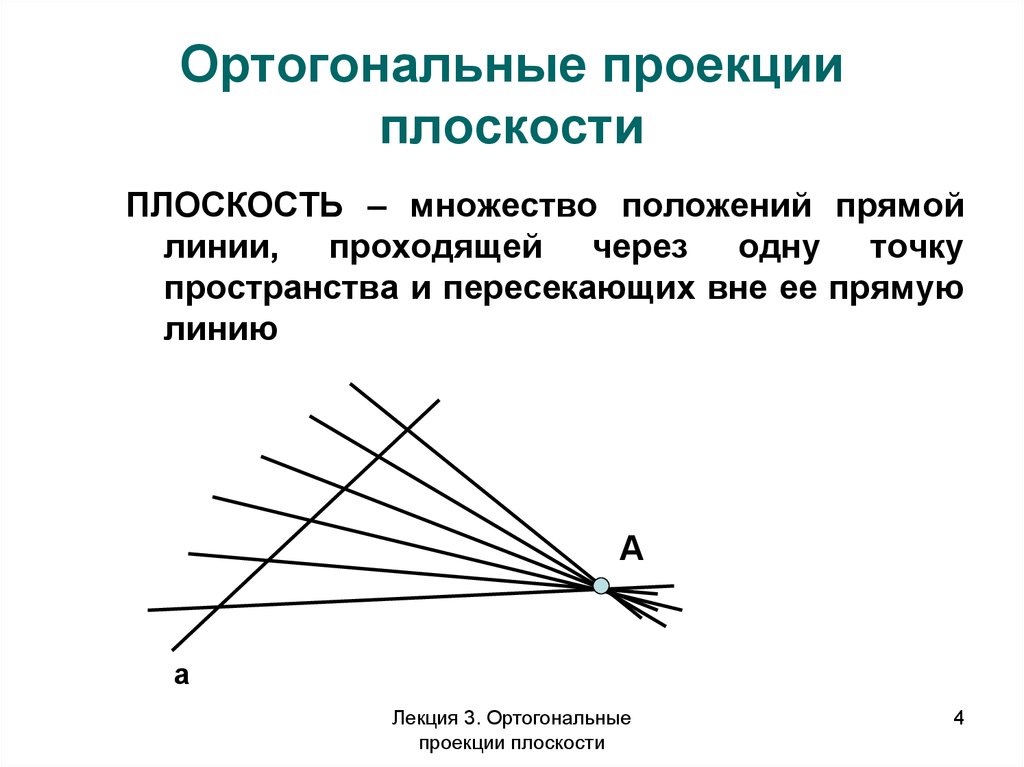
4. Ортогональные проекции плоскости

ПЛОСКОСТЬ – множество положений прямой
линии, проходящей через одну точку
пространства и пересекающих вне ее прямую
линию
A
a
Лекция 3. Ортогональные
проекции плоскости
4

5.

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ
1. Аналитический способ
Аx + By + Cz + D = 0
2. Графические способы
Лекция 3. Ортогональные
проекции плоскости
5

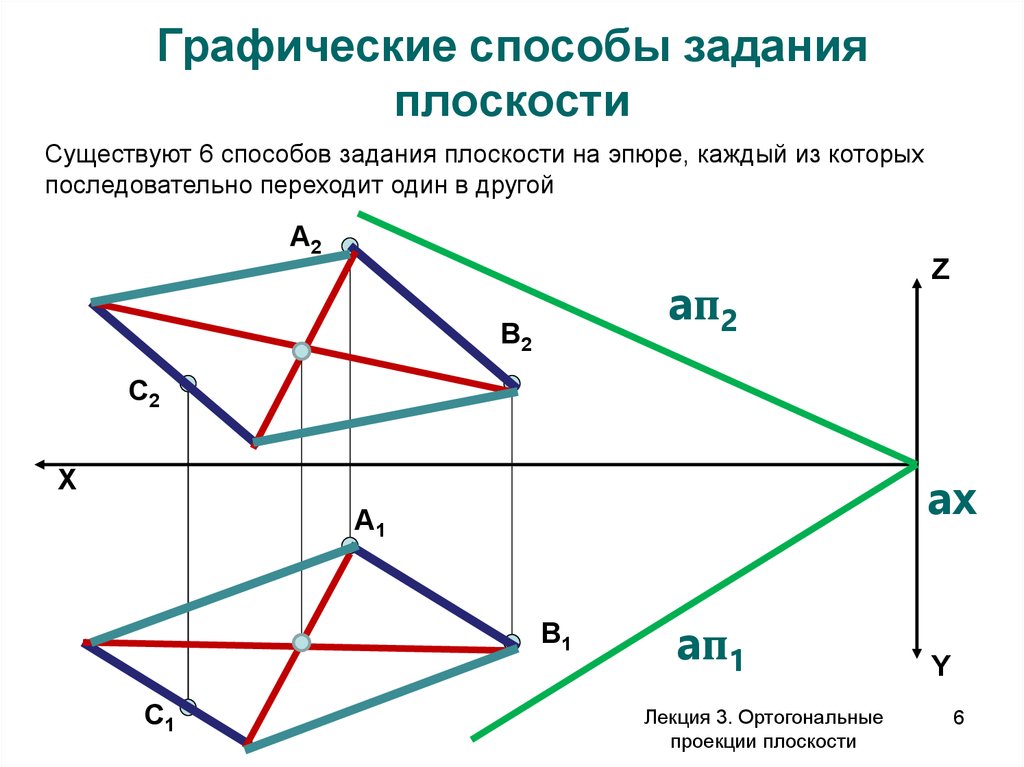
6. Графические способы задания плоскости

Существуют 6 способов задания плоскости на эпюре, каждый из которых
последовательно переходит один в другой
А2
aп2
В2
Z
C2
ax
X
А1
В1
C1
aп1
Лекция 3. Ортогональные
проекции плоскости
Y
6

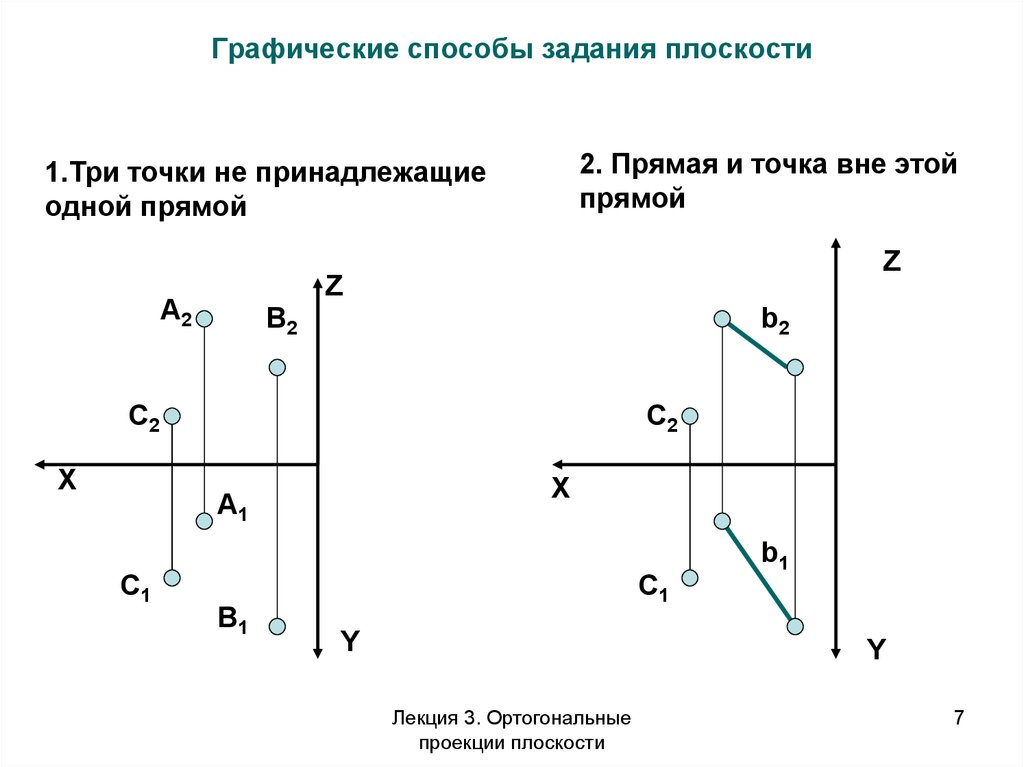
7. Графические способы задания плоскости

2. Прямая и точка вне этой
прямой
1.Три точки не принадлежащие
одной прямой
Z
Z
А2
В2
b2
C2
X
C2
X
А1
b1
C1
В1
C1
Y
Y
Лекция 3. Ортогональные
проекции плоскости
7

8.

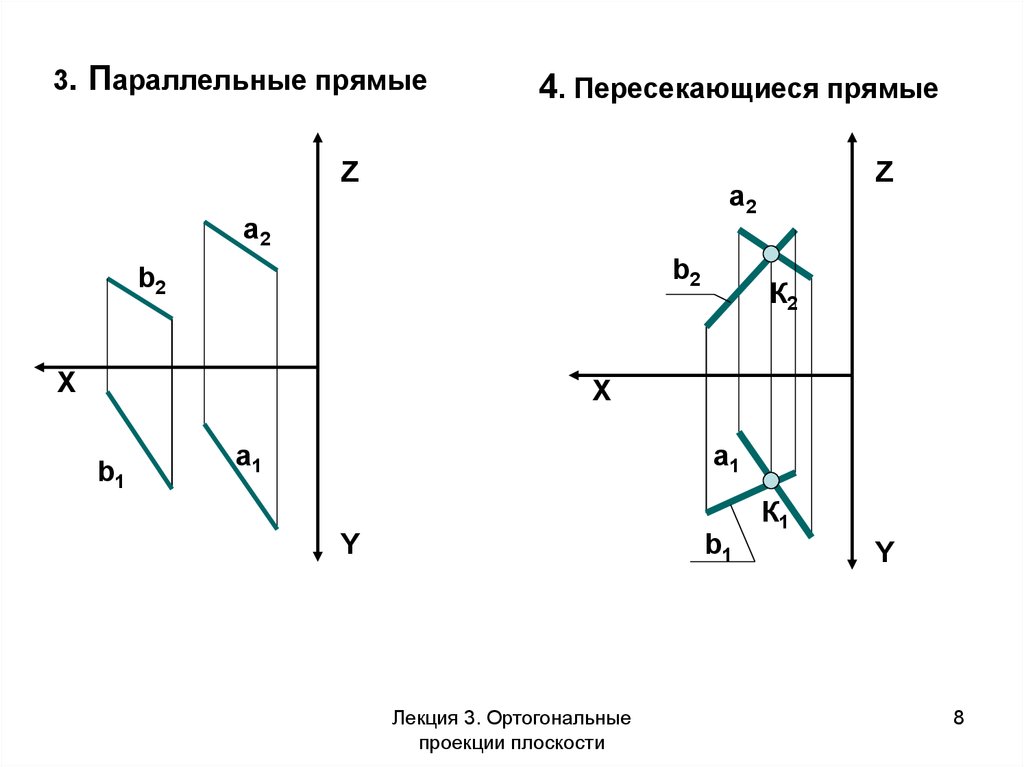
3. Параллельные прямые
4. Пересекающиеся прямые
Z
a2
а2
b2
b2
X
Z
К2
X
b1
а1
a1
К1
Y
b1
Лекция 3. Ортогональные
проекции плоскости
Y
8

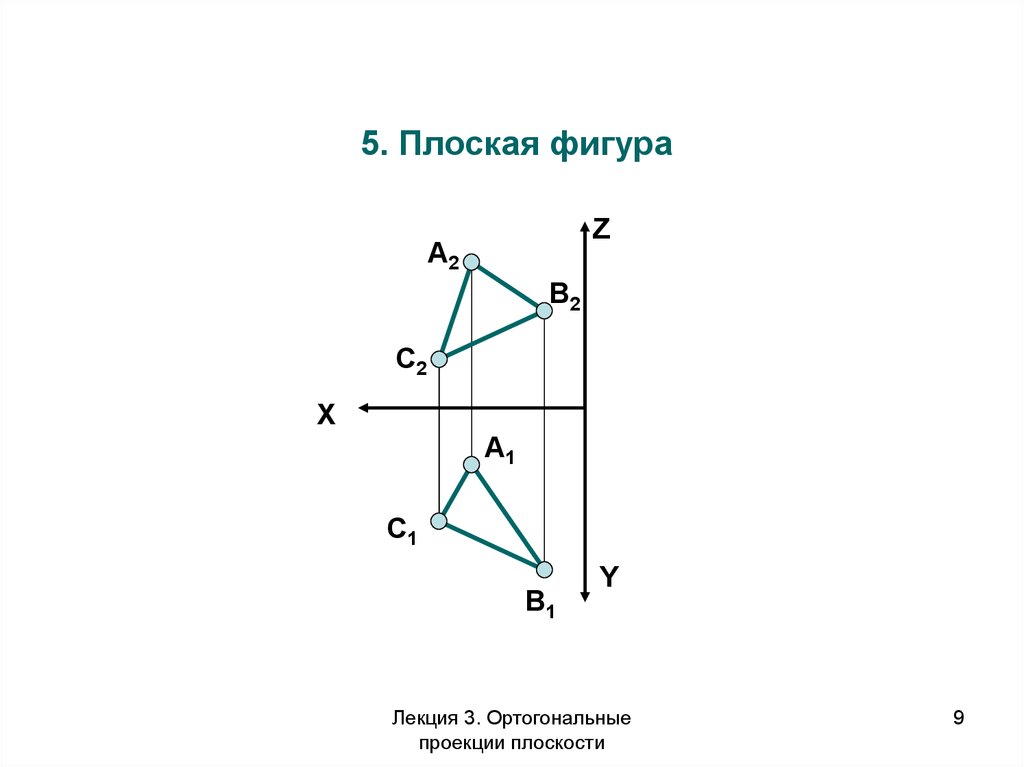
9.

5. Плоская фигура
Z
А2
В2
C2
X
А1
C1
В1
Y
Лекция 3. Ортогональные
проекции плоскости
9

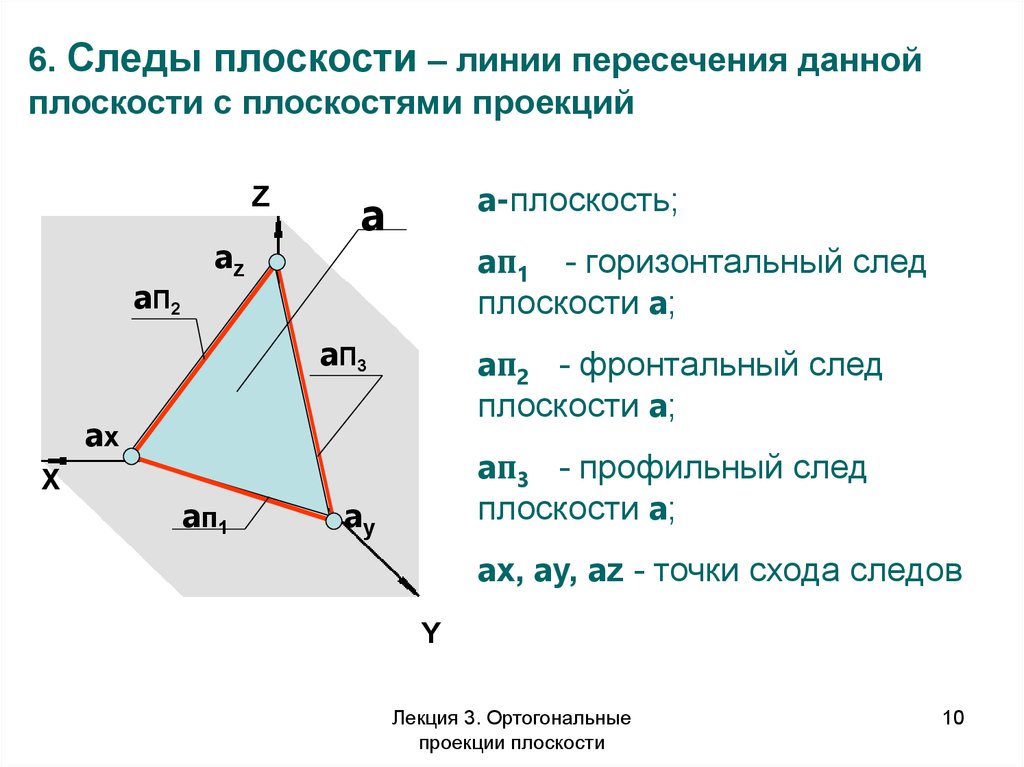
10.

6. Следы плоскости – линии пересечения данной
плоскости с плоскостями проекций
Z
a П2
az
a-плоскость;
a
aп1 - горизонтальный след
плоскости a;
a П3
aп2 - фронтальный след
плоскости a;
ax
X
a п1
aп3 - профильный след
плоскости a;
ay
ax, ay, az - точки схода следов
Y
Лекция 3. Ортогональные
проекции плоскости
10

11.

Z
a П2
Z
a
az
az
a П3
a П2
a П3
Zα
ax
X
X
a п1
Y
xα
ax
ay
ay
Y
yα
a п1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
11

12. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

1. Относительно плоскостей проекций плоскости в
пространстве занимают:
• общее положение
• частное положение
2. Плоскости частного положения подразделяют на
• плоскости параллельные плоскостям проекций –
плоскости уровня
• плоскости
перпендикулярные
плоскостям
проекций – плоскости проецирующие
Лекция 3. Ортогональные
проекции плоскости
12

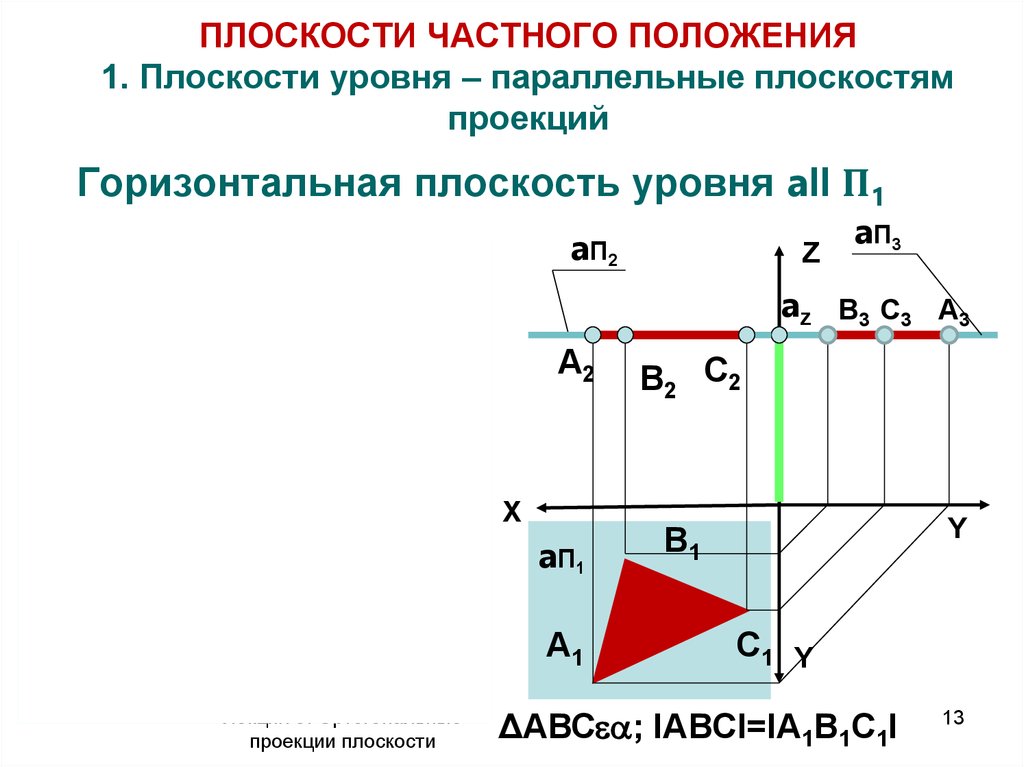
13. ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ 1. Плоскости уровня – параллельные плоскостям проекций

Горизонтальная плоскость уровня aII П1
a П2
a
Z
В2 С az
2
А2
aП2
a П3
А2
В1
А1
a П1
С1
a П3
az В3 С3 А3
X
X
Z
Y
Лекция 3. Ортогональные
проекции плоскости
А1
В2 С2
Y
В1
С1 Y
ΔАВС ; IABCI=IA1B1C1I
13

14.

Фронтальная плоскость уровня bI I П2
Z
b
bП2
В2
Z
В3
bП 3
А2
С2
bП 3
Y
X
bп1
А3≡С3
by
X
by
А1
Y
bп1
Лекция 3. Ортогональные
проекции плоскости
ΔАВС ;
В1
С1
by
Y
IABCI=IA2B2C2I
14

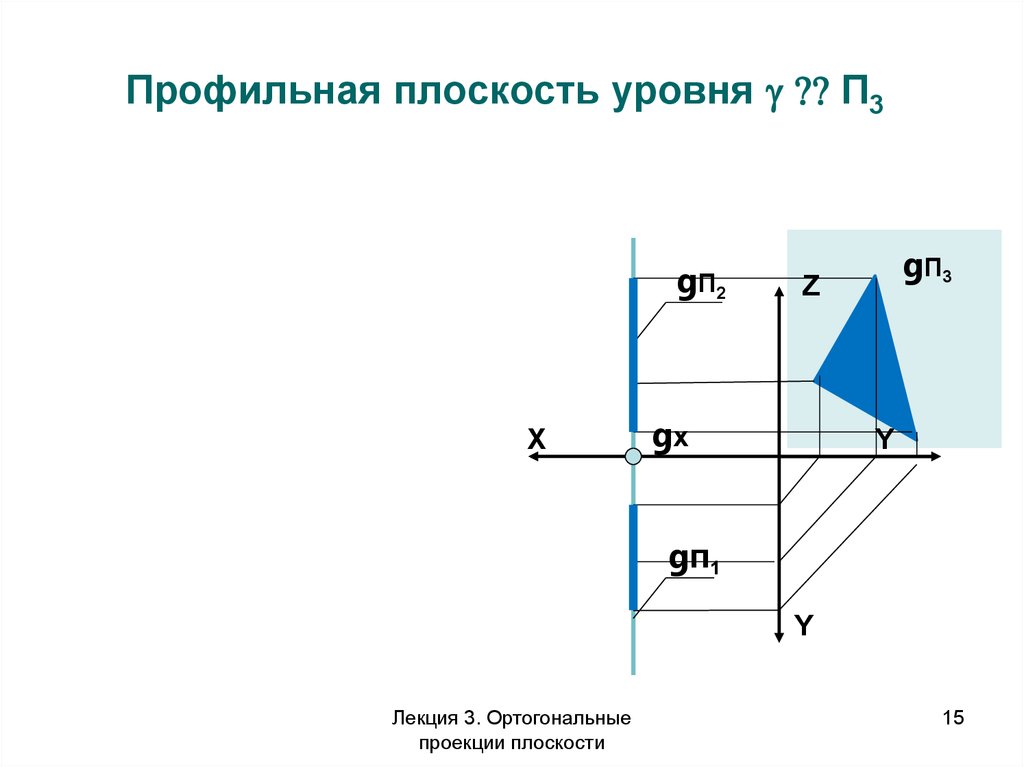
15.

Профильная плоскость уровня П3
Z
g
g П2
g П2
X gx
X
g п1
Y
g П3
Z
gx
Y
gп1
Y
Лекция 3. Ортогональные
проекции плоскости
15

16. Особенности чертежа плоскостей уровня

• Фигуры принадлежащие плоскостям уровня
проецируются в натуральную величину на
параллельную плоскость проекций
• На другие плоскости проекций фигуры
принадлежащие плоскостям уровня
проецируются в прямую линию
Лекция 3. Ортогональные
проекции плоскости
16

17.

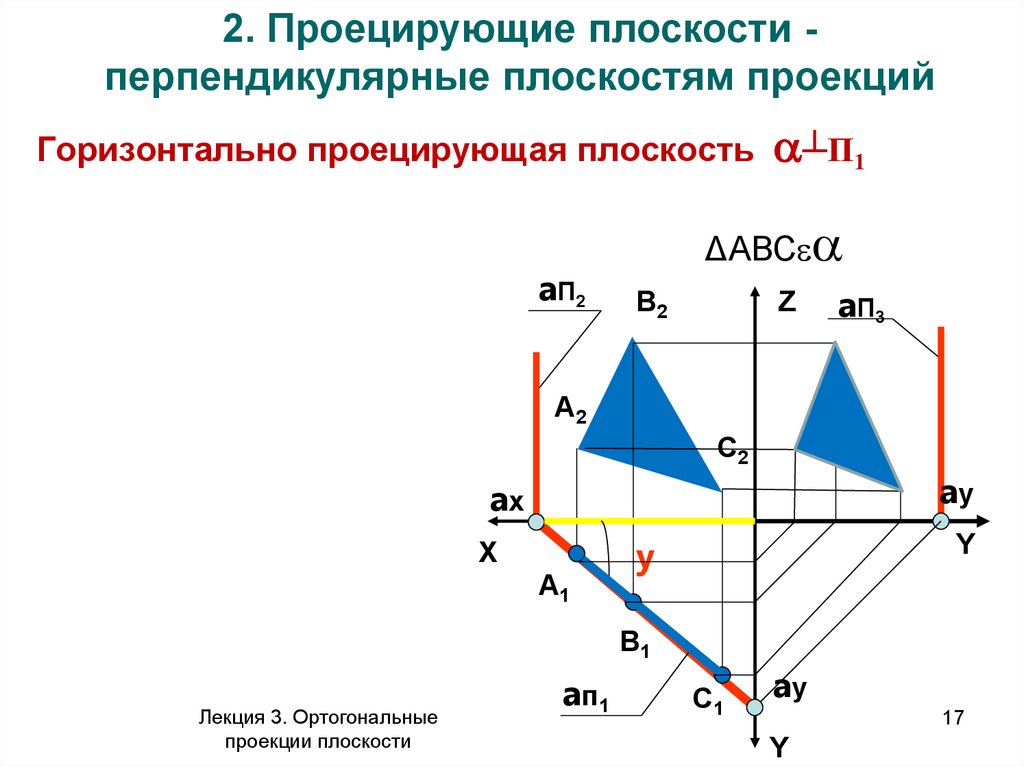
2. Проецирующие плоскости перпендикулярные плоскостям проекций
Горизонтально проецирующая плоскость
Z
a П2
a П2
a
┴П1
ΔАВС
В2
Z
a П3
А2
X
С2
a П3
ax
ay
ax
X
a п1
ay
А1
y
Y
В1
Y
Лекция 3. Ортогональные
проекции плоскости
a п1
С1
ay
17
Y

18.

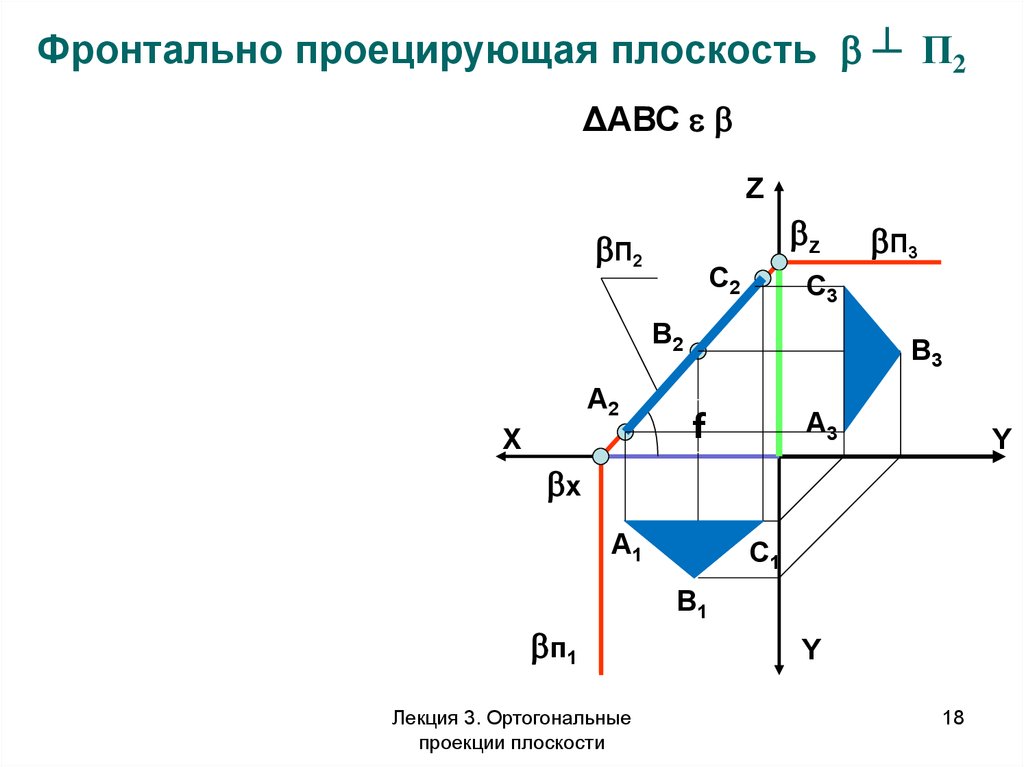
Фронтально проецирующая плоскость ┴ П2
ΔАВС
Z
П2
Z
z
П2
z
С2
С3
В2
П3
x
А2
X
П3
В3
f
А3
Y
x
X
П1
А1
С1
В1
Y
п1
Лекция 3. Ортогональные
проекции плоскости
Y
18

19.

Профильно проецирующая плоскость ┴ П3
ΔАВС
Z
П2
Z
z
П2
z
В2
А2
П3
С2
φ
X
X
В1
п1
y
А1
Y
Лекция 3. Ортогональные
проекции плоскости
Y
y
С1
п1
П3
В3
ψ А3 С3
y
Y
19

20.

Особенности чертежа проецирующих
плоскостей
• Фигуры принадлежащие проецирующим
плоскостям проецируются в прямую линию
на перпендикулярную плоскость проекций
(вырожденная проекция)
• Угол между заданной плоскостью и
плоскостью проекций равен углу наклона
между вырожденной проекцией и осями
координат
Лекция 3. Ортогональные
проекции плоскости
20

21. Ортогональные проекции плоскости общего положения

Лекция 3. Ортогональные
проекции плоскости
21

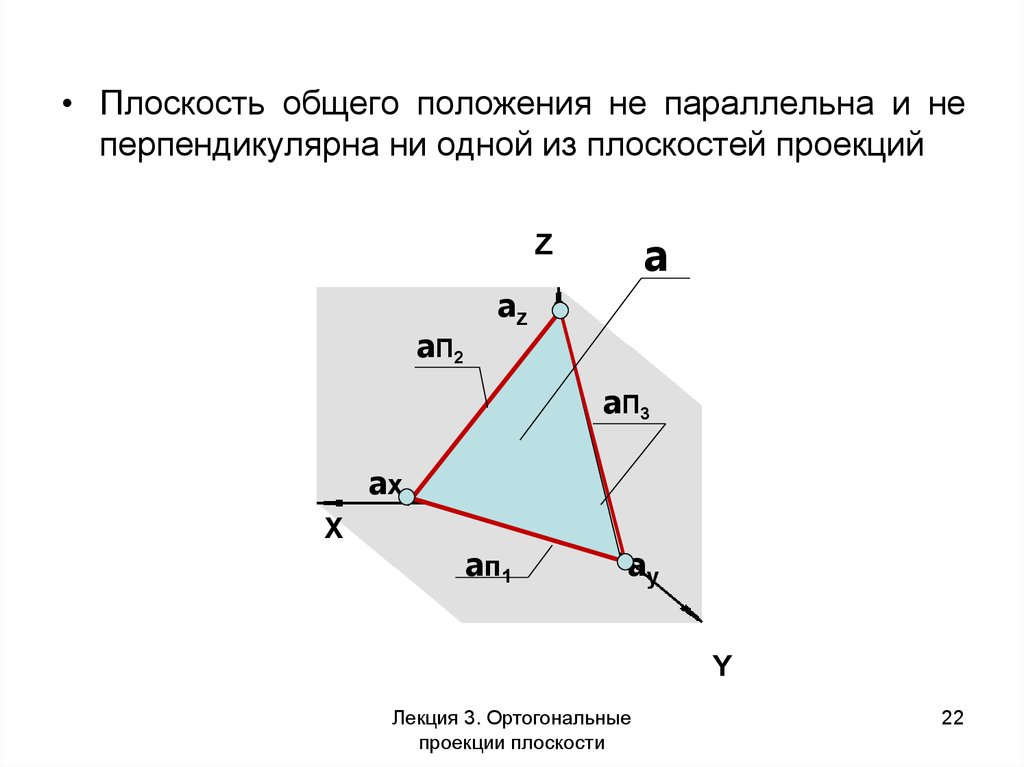
22.

• Плоскость общего положения не параллельна и не
перпендикулярна ни одной из плоскостей проекций
a
Z
a П2
az
a П3
ax
X
a п1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
22

23.

Принадлежность точки и
прямой линии плоскости
1. Точка принадлежит плоскости, если она
принадлежит прямой в этой плоскости
2. Прямая принадлежит плоскости если она проходит:
а) через две точки этой плоскости;
б) через точку плоскости параллельно какойлибо прямой в этой плоскости
Лекция 3. Ортогональные
проекции плоскости
23

24.

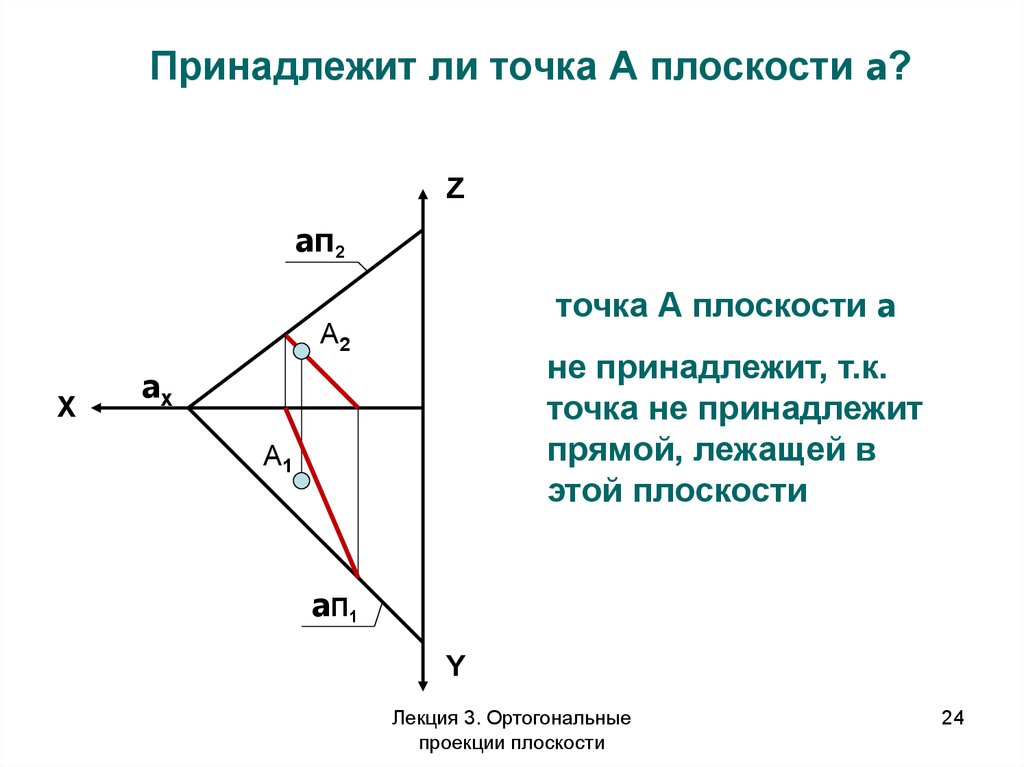
Принадлежит ли точка А плоскости a?
Z
aп2
точка А плоскости a
А2
X
не принадлежит, т.к.
точка не принадлежит
прямой, лежащей в
этой плоскости
ax
А1
a П1
Y
Лекция 3. Ортогональные
проекции плоскости
24

25. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ

1.
Линии уровня плоскости – линии параллельные
плоскостям проекций и принадлежащие данной
плоскости;
2.
Линии наибольшего наклона плоскости (ЛНН) –
определяют угол наклона данной плоскости к
одной из плоскостей проекций.
ЛНН перпендикулярны линиям уровня:
горизонтали на плоскости П1;
фронтали на плоскости П2.
Лекция 3. Ортогональные
проекции плоскости
25

26.

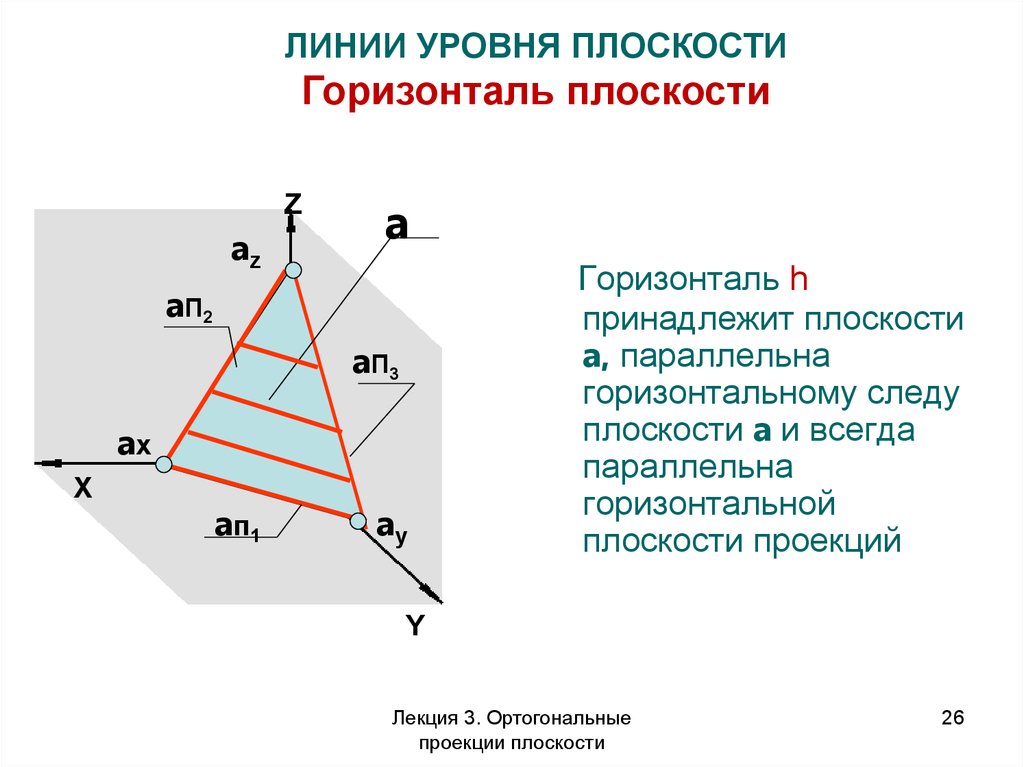
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости
Z
az
a
a П2
a П3
ax
X
a п1
ay
Горизонталь h
принадлежит плоскости
a, параллельна
горизонтальному следу
плоскости a и всегда
параллельна
горизонтальной
плоскости проекций
Y
Лекция 3. Ортогональные
проекции плоскости
26

27.

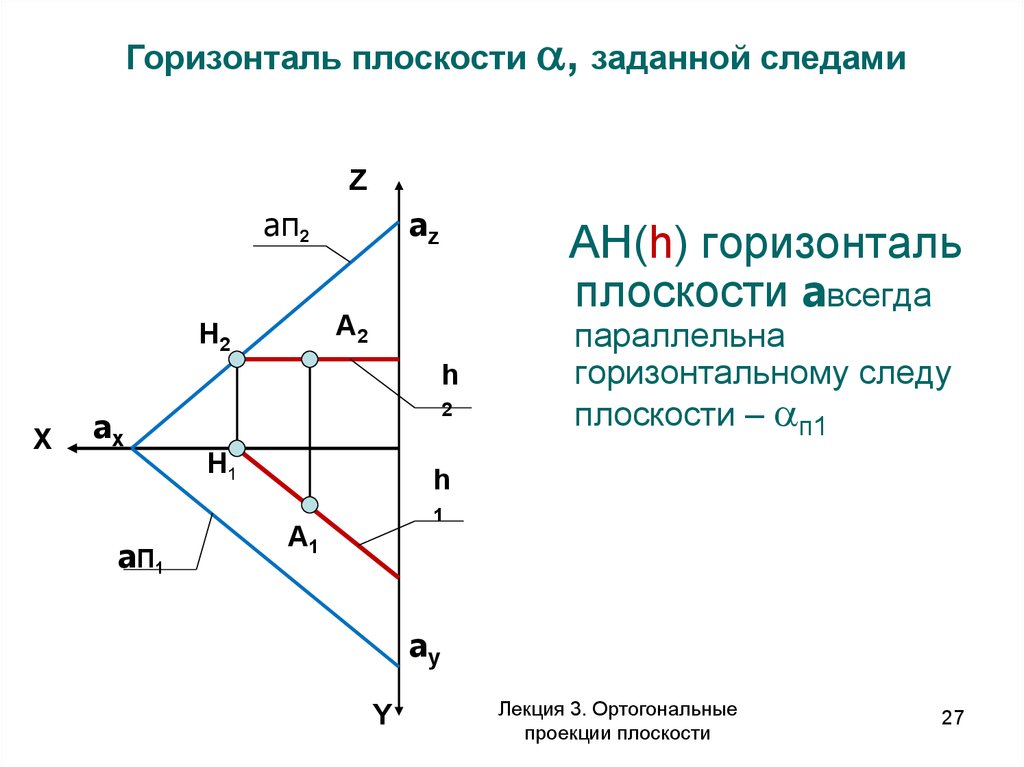
Горизонталь плоскости , заданной следами
Z
aп2
az
AН(h) горизонталь
плоскости aвсегда
А2
Н2
h
X
ax
a П1
2
Н1
параллельна
горизонтальному следу
плоскости – п1
h
1
А1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
27

28.

Горизонталь плоскости треугольника
В2
AH(h)–
горизонталь
ΔАВС
H2
А2
X
С2
А1
С1
H1
В1
Лекция 3. Ортогональные
проекции плоскости
28

29.

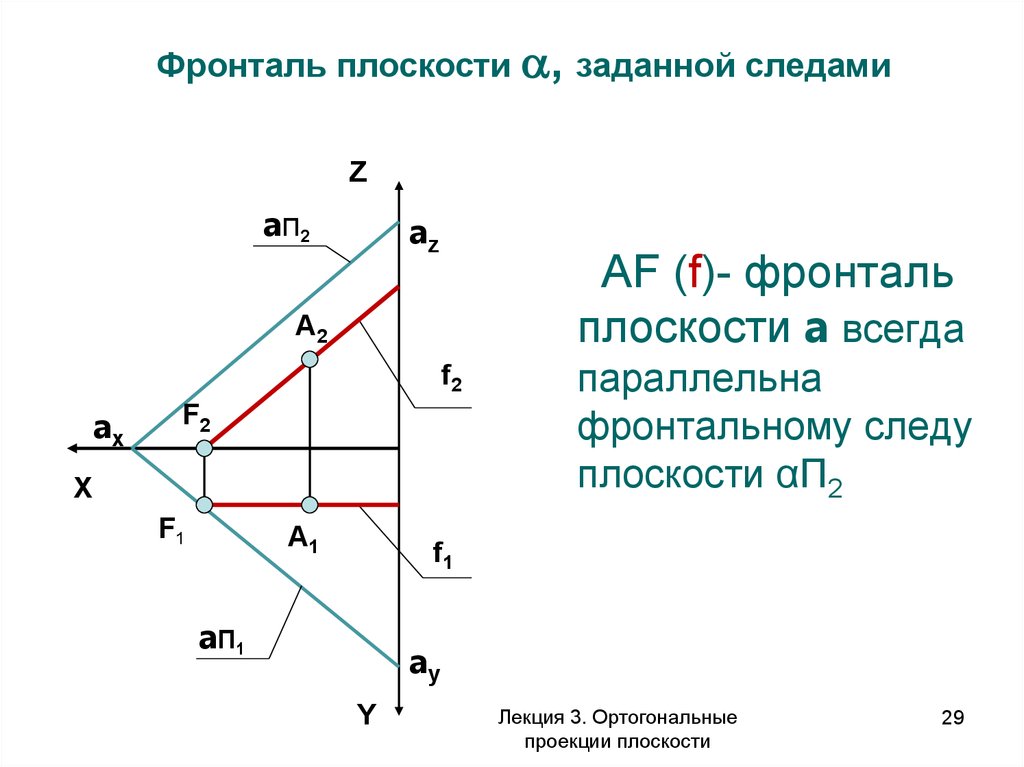
Фронталь плоскости , заданной следами
Z
aп2
az
АF (f)- фронталь
плоскости a всегда
А2
f2
ax
F2
X
F1
А1
параллельна
фронтальному следу
плоскости αП2
f1
a П1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
29

30.

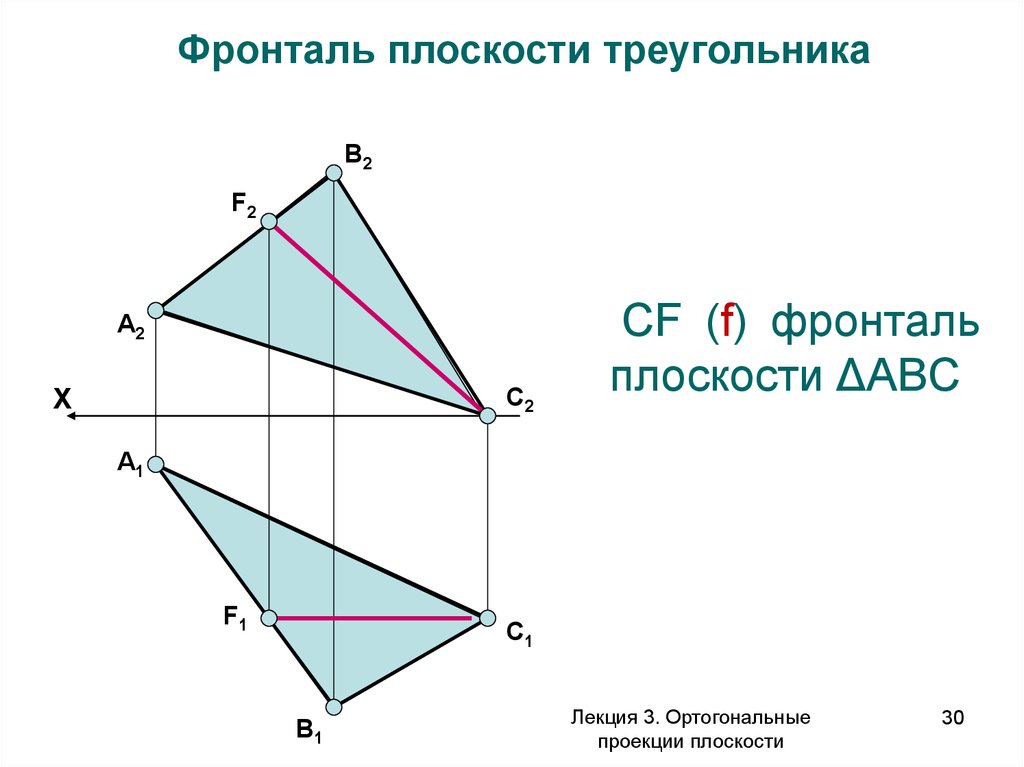
Фронталь плоскости треугольника
В2
F2
А2
С2
X
СF (f) фронталь
плоскости ΔАВС
А1
F1
С1
В1
Лекция 3. Ортогональные
проекции плоскости
30

31.

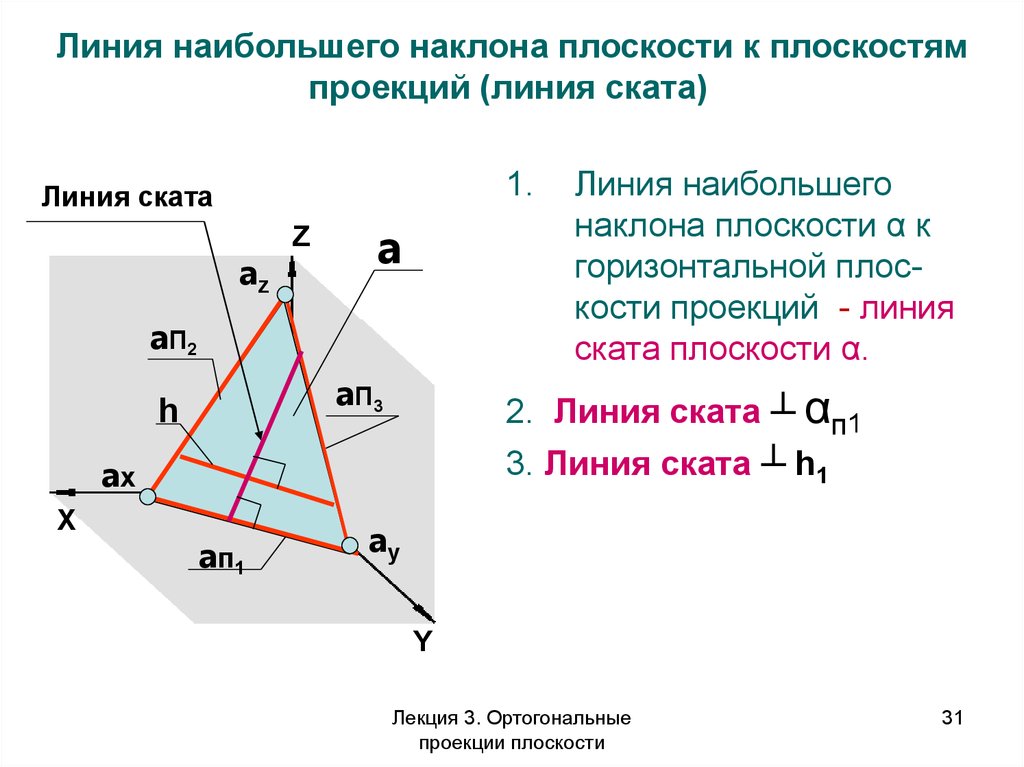
Линия наибольшего наклона плоскости к плоскостям
проекций (линия ската)
1.
Линия ската
az
Z
a
a П2
aП3
h
2. Линия ската ┴ αп1
3. Линия ската ┴ h1
ax
X
Линия наибольшего
наклона плоскости α к
горизонтальной плоскости проекций - линия
ската плоскости α.
a п1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
31

32.

Линия ската на горизонтальной плоскости
проекций перпендикулярна горизонтали
плоскости
aп2
az
А2
H2
h2
X
ax
D2
H1
А1D1 ┴ А1H1 II П1
А1D1 ┴ αп1
h1
А1
a П1
D1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
32

33.

Линия ската треугольника из наивысшей
точки (В) перпендикулярна горизонтали
В2
H2
А2
D2
С2
X
В1D1 ┴ А1H1
ВD – линия ската
треугольника
А1
D1
С1
H1
В1
Лекция 3. Ортогональные
проекции плоскости
33

34.

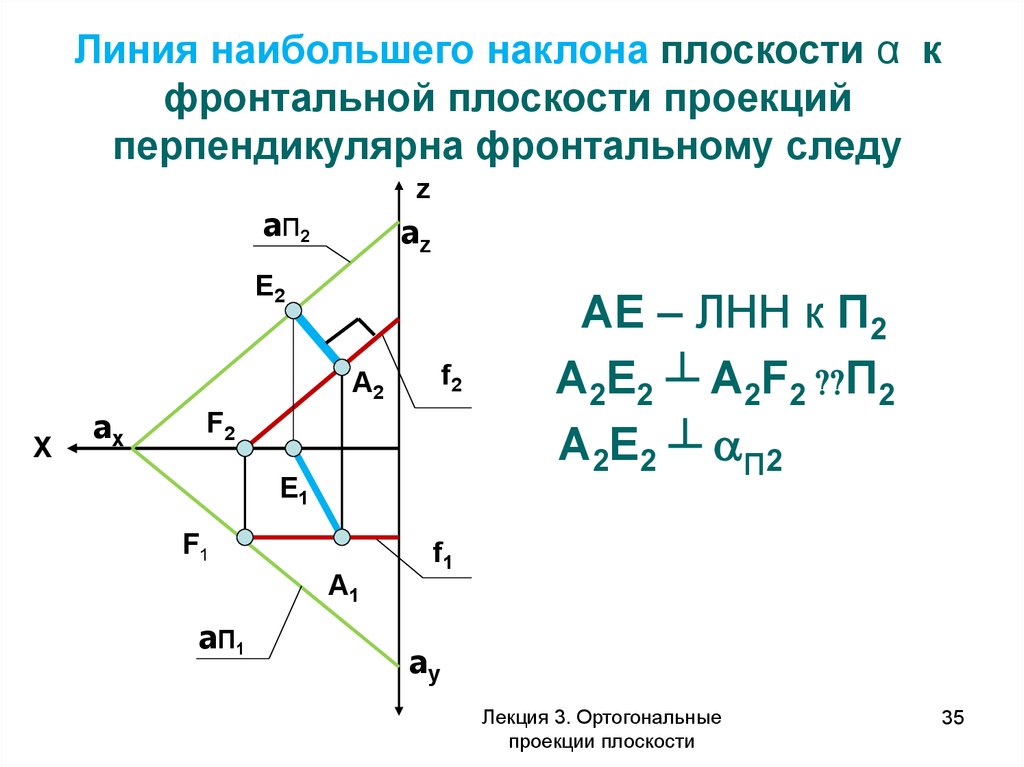
Линия наибольшего наклона плоскости α к
фронтальной плоскости проекций
перпендикулярна фронтали
Z
a П2
a
az
ЛНН к П2 ┴ αп2
ЛНН к П2 ┴ f II П2
aП3
ax
X
f
a п1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
34

35.

Линия наибольшего наклона плоскости α к
фронтальной плоскости проекций
перпендикулярна фронтальному следу
z
aп2
az
Е2
f2
А2
X
ax
F2
Е1
F1
АЕ – ЛНН к П2
A2Е2 ┴ A2F2 П2
A2Е2 ┴ п2
f1
A1
a П1
ay
Лекция 3. Ортогональные
проекции плоскости
35

36.

Линия наибольшего наклона (линия ската)
плоскости ΔАВС к фронтальной плоскости проекций
перпендикулярна фронтали
В2
F2
Е2
А2
С2
X
А1
F1
Е1
В1
BE – ЛНН к П2
В2E2 ┴ C2F2 П2
С1
Лекция 3. Ортогональные
проекции плоскости
36

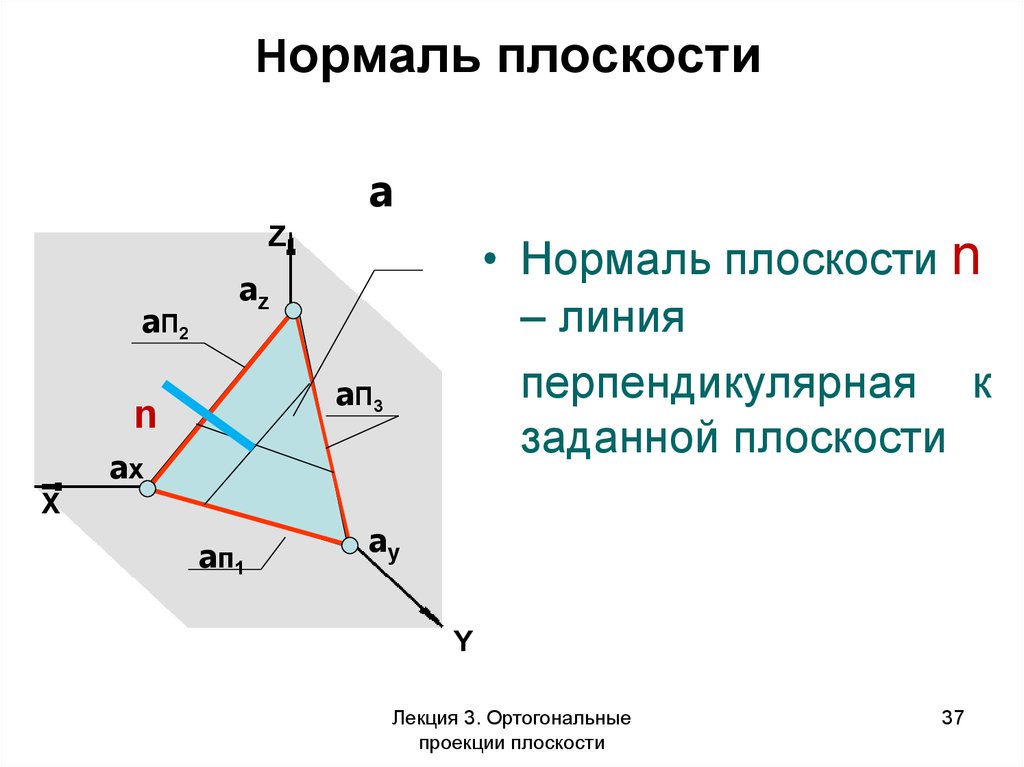
37. Нормаль плоскости

a
Z
a П2
• Нормаль плоскости n
– линия
перпендикулярная к
заданной плоскости
az
aП3
n
ax
X
a п1
ay
Y
Лекция 3. Ортогональные
проекции плоскости
37

38.

aп2
az
n2
А2
ax
А1
X
n1
ay
aП1
Y
• Проекции
нормали
перпендикулярны проекциям линий уровня
плоскости a:
горизонтали на П1
фронтали на П2
• Проекции нормали перпендикулярны следам
плоскости a:
n1 ┴ aп1
n2 ┴ aп2
Лекция 3. Ортогональные
проекции плоскости
38

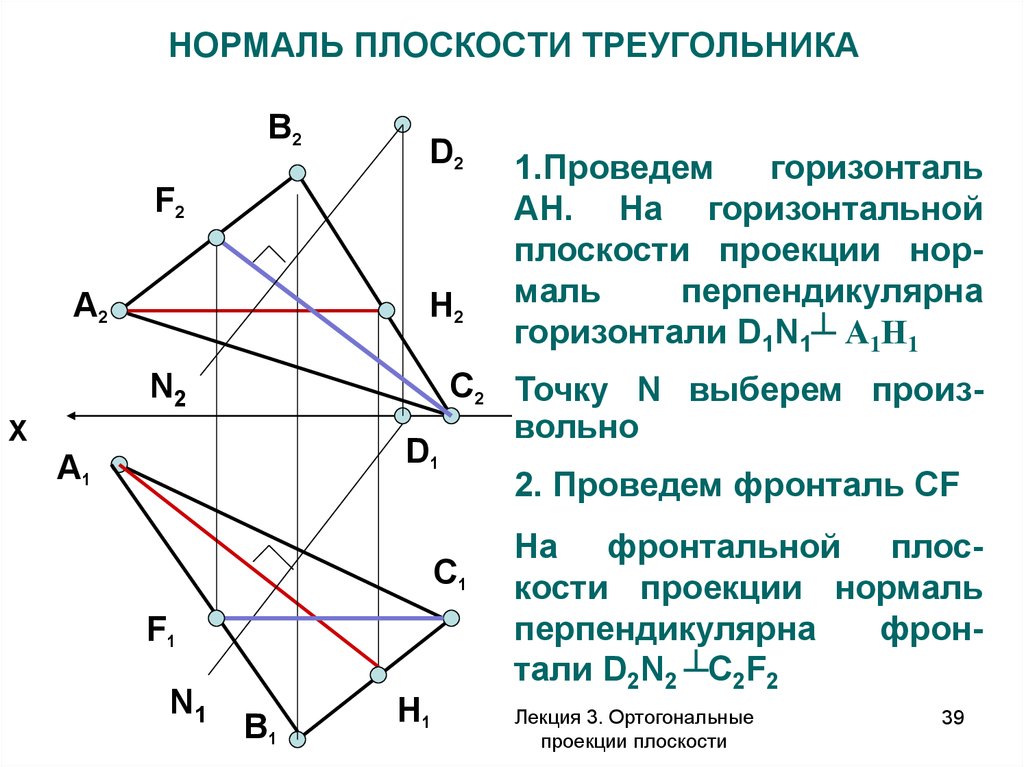
39. НОРМАЛЬ ПЛОСКОСТИ ТРЕУГОЛЬНИКА

А2
НОРМАЛЬ ПЛОСКОСТИ ТРЕУГОЛЬНИКА
Через точку D
провести
В2
D2 1.Проведем перпендикуляр
горизонталь
F2
к
плоскости
AH. На горизонтальной
плоскости треугольника
проекции норАВС
перпендикулярна
H2 маль
горизонталиА(80,20,30)
D1N1┴ А1Н1
С2 Точку N выберем произВ(40,60,60)
вольно
D1
2. ПроведемС(0,40,0)
фронталь CF
N2
X
А1
С1
F1
N1
В1
H1
D(10,0,70) плосНа фронтальной
кости проекции нормаль
перпендикулярна
фронтали D2N2 ┴C2F2
Лекция 3. Ортогональные
проекции плоскости
39

40. Относительное положение прямой и плоскости Относительное положение плоскостей

Лекция 3. Ортогональные
проекции плоскости
40

41.

ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ
И ПЛОСКОСТЬ
Параллельные плоскости
Лекция 3. Ортогональные
проекции плоскости
41

42.

1.
Прямая параллельна плоскости, если она
параллельна любой прямой, лежащей в этой
плоскости
2.
Плоскости
параллельны,
если
две
пересекающиеся прямые одной плоскости,
параллельны
двум
пересекающимся
прямым другой плоскости
Лекция 3. Ортогональные
проекции плоскости
42

43.

• Через точку D провести прямую a
параллельную Δ АВС и плоскость
α(a∩b) параллельную Δ АВС
Лекция 3. Ортогональные
проекции плоскости
43

44.

a2
B2
b2
Z
D2
A2
a2 II B2C2
a II BC
a1 II B1C1
a II ΔABC
C2
(a b)
X
b1
A1
a II BC
D1
C1
a II ΔABC
b II AC
a1
B1
Y
Лекция 3. Ортогональные
проекции плоскости
44

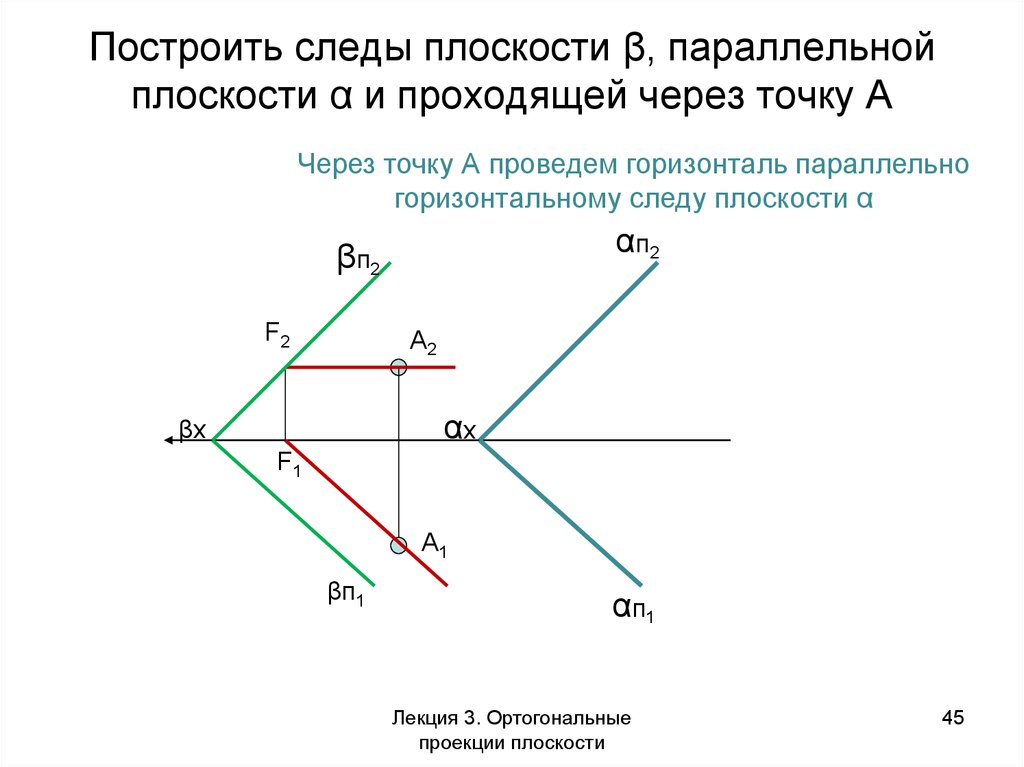
45. Построить следы плоскости β, параллельной плоскости α и проходящей через точку А

Через точку А проведем горизонталь параллельно
горизонтальному следу плоскости α
αп2
βп2
F2
А2
αх
βх
F1
А1
βп1
αп1
Лекция 3. Ортогональные
проекции плоскости
45

46. Прямая перпендикулярная плоскости, перпендикулярные плоскости

• Прямая перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся прямым,
принадлежащим данной плоскости
• В соответствии с теоремой о проекциях прямого угла
прямая перпендикулярна плоскости, если она
перпендикулярна одноименным проекциям горизонтали и
фронтали плоскости
· Две плоскости перпендикулярны, если одна плоскость
проходит через перпендикуляр к другой
Лекция 3. Ортогональные
проекции плоскости
46

47. Задача

• Построить проекции нормали плоскости
a, проходящей через точку С,
принадлежащей данной плоскости
Лекция 3. Ортогональные
проекции плоскости
47

48.

C α
αп2
n2
X
С2
А2
αх D2
А1
С1
O
D1
n1
αП1
Лекция 3. Ортогональные
проекции плоскости
48

49.

• Через точку D провести перпендикуляр
к плоскости Δ АВС и плоскость α (n∩a)
перпендикулярную Δ АВС
• А(80,10,30)
• В(40,60,50)
• С(10,45,0)
• D(50,55,5)
Лекция 3. Ортогональные
проекции плоскости
49

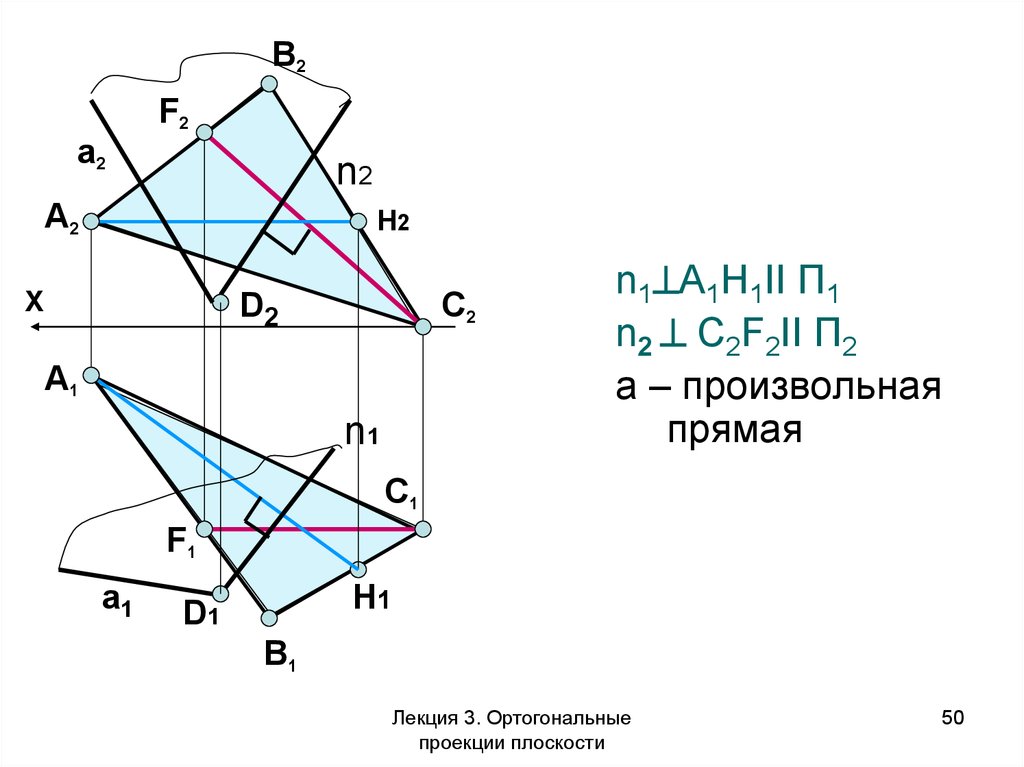
50.

В2
F2
a2
n2
А2
H2
X
С2
D2
А1
n1
n1 А1Н1II П1
n2 С2F2II П2
а – произвольная
прямая
С1
F1
a1
H1
D1
В1
Лекция 3. Ортогональные
проекции плоскости
50

51. ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ

ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮТСЯ,
ЕСЛИ У НИХ ЕСТЬ ОДНА ОБЩАЯ ТОЧКА
Лекция 3. Ортогональные
проекции плоскости
51

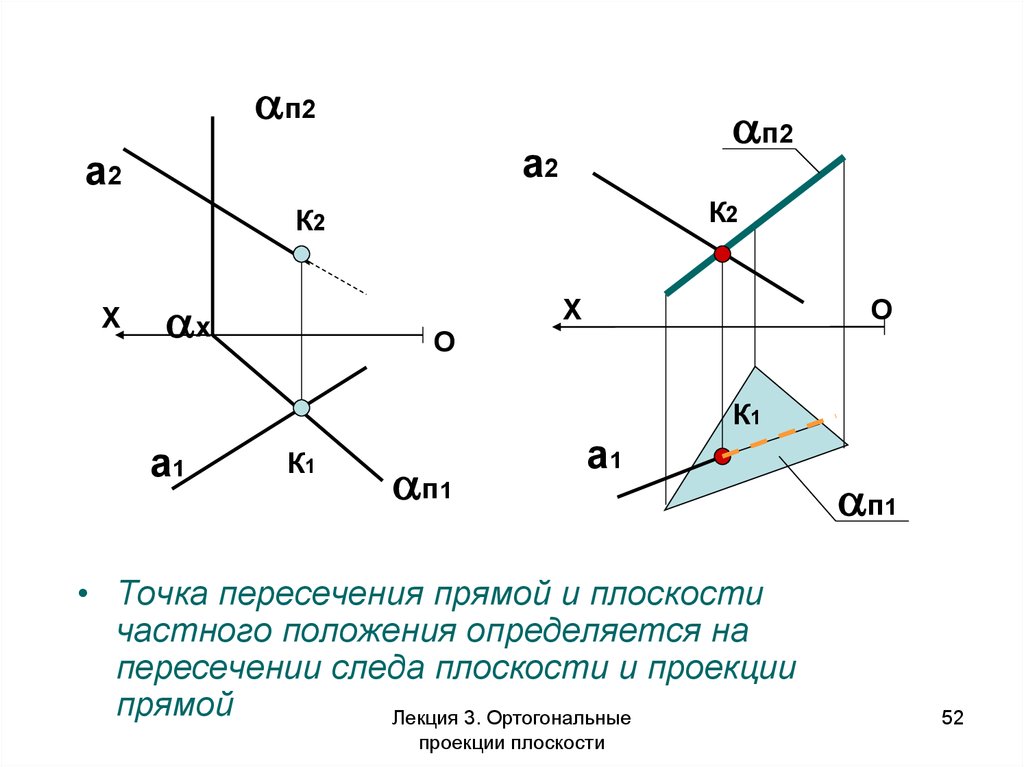
52.

п2
п2
а2
а2
К2
К2
X
х
X
O
O
К1
a1
К1
п1
a1
• Точка пересечения прямой и плоскости
частного положения определяется на
пересечении следа плоскости и проекции
прямой
Лекция 3. Ортогональные
проекции плоскости
п1
52

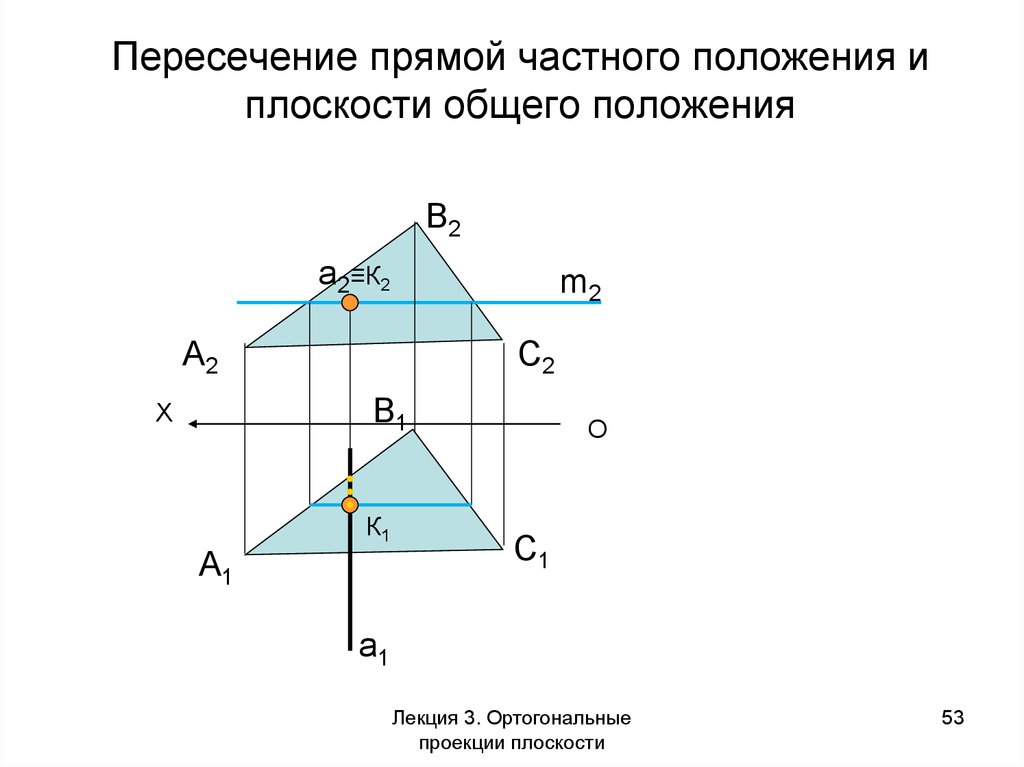
53. Пересечение прямой частного положения и плоскости общего положения

В2
a2≡К2
m2
А2
С2
В1
X
А1
К1
О
С1
a1
Лекция 3. Ортогональные
проекции плоскости
53

54. Пересечение прямой общего положения и плоскости общего положения

СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ
ПЛОСКОСТЕЙ
Лекция 3. Ортогональные
проекции плоскости
54

55. Алгоритм способа плоскостей

• Прямую заключают в плоскость частного
положения α ┴ П1
• Определяют линию пересечения заданной
плоскости и вспомогательной плоскости α
• Определяют точку пересечения заданной
прямой и построенной линии пересечения
• Это искомая точка пересечения заданной
плоскости и прямой а
• Определяют видимость заданной прямой
Лекция 3. Ортогональные
проекции плоскости
55

56.

B2
αп2
a2
К2
D2
С2
Е2
A2
B1
αп1
D1
К1
C1
E1
A1
a1
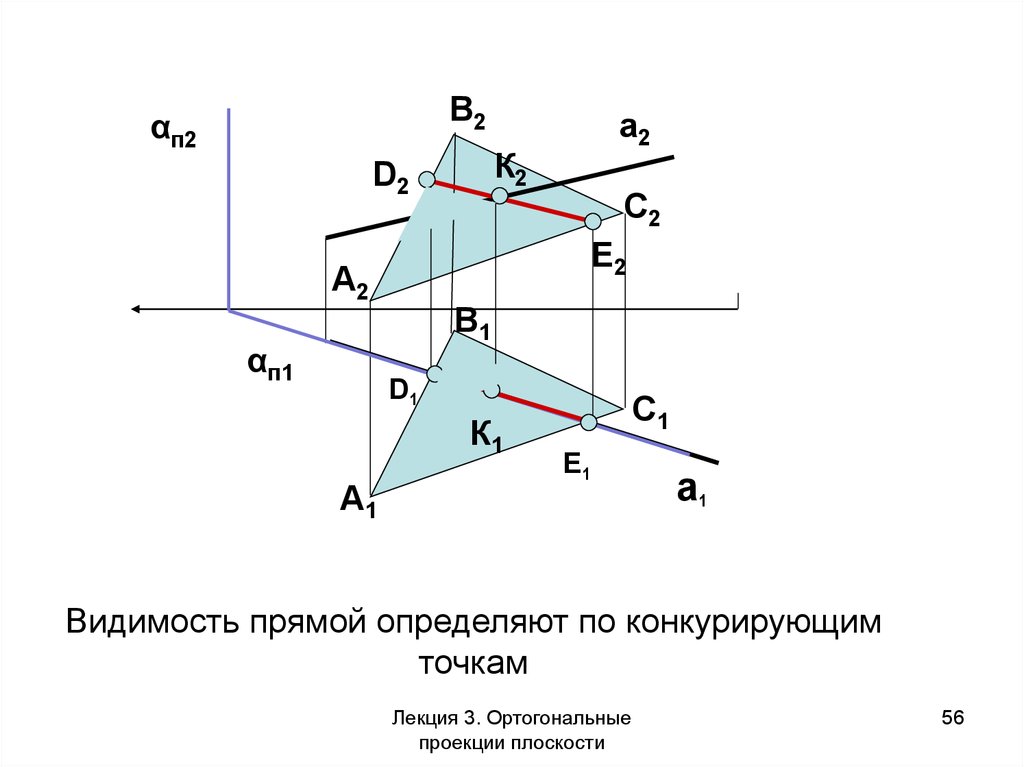
Видимость прямой определяют по конкурирующим
точкам
Лекция 3. Ортогональные
проекции плоскости
56

57.

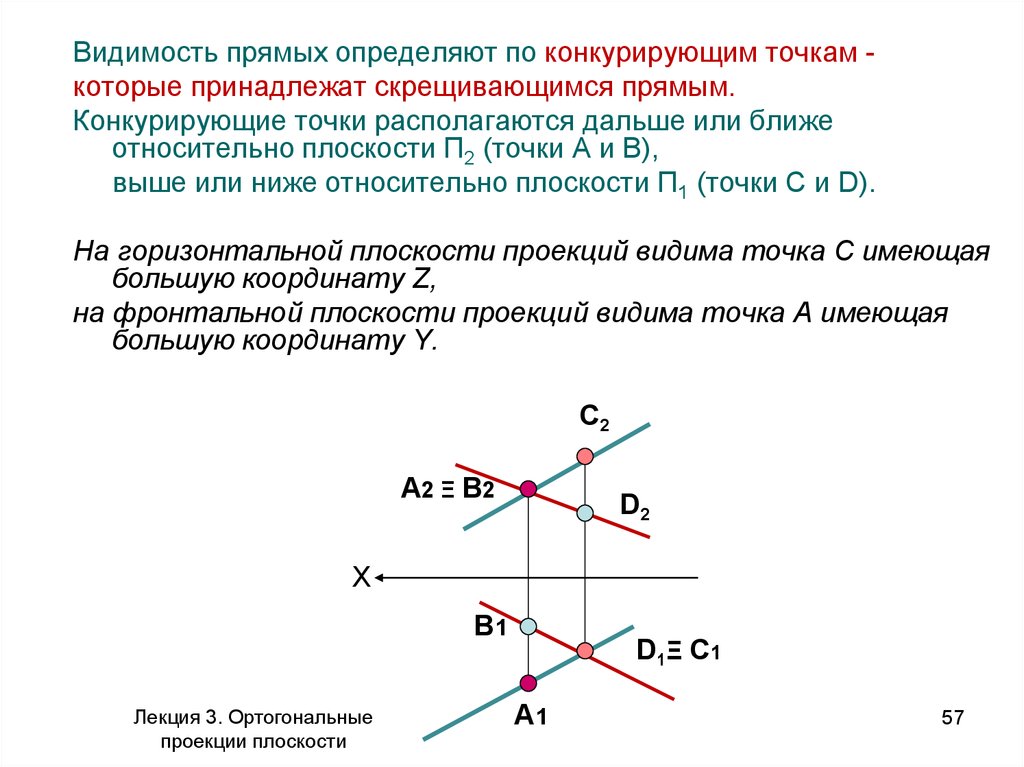
Видимость прямых определяют по конкурирующим точкам которые принадлежат скрещивающимся прямым.
Конкурирующие точки располагаются дальше или ближе
относительно плоскости П2 (точки А и В),
выше или ниже относительно плоскости П1 (точки C и D).
На горизонтальной плоскости проекций видима точка С имеющая
большую координату Z,
на фронтальной плоскости проекций видима точка А имеющая
большую координату Y.
С2
А2 Ξ В2
D2
X
В1
Лекция 3. Ортогональные
проекции плоскости
D1Ξ C1
А1
57

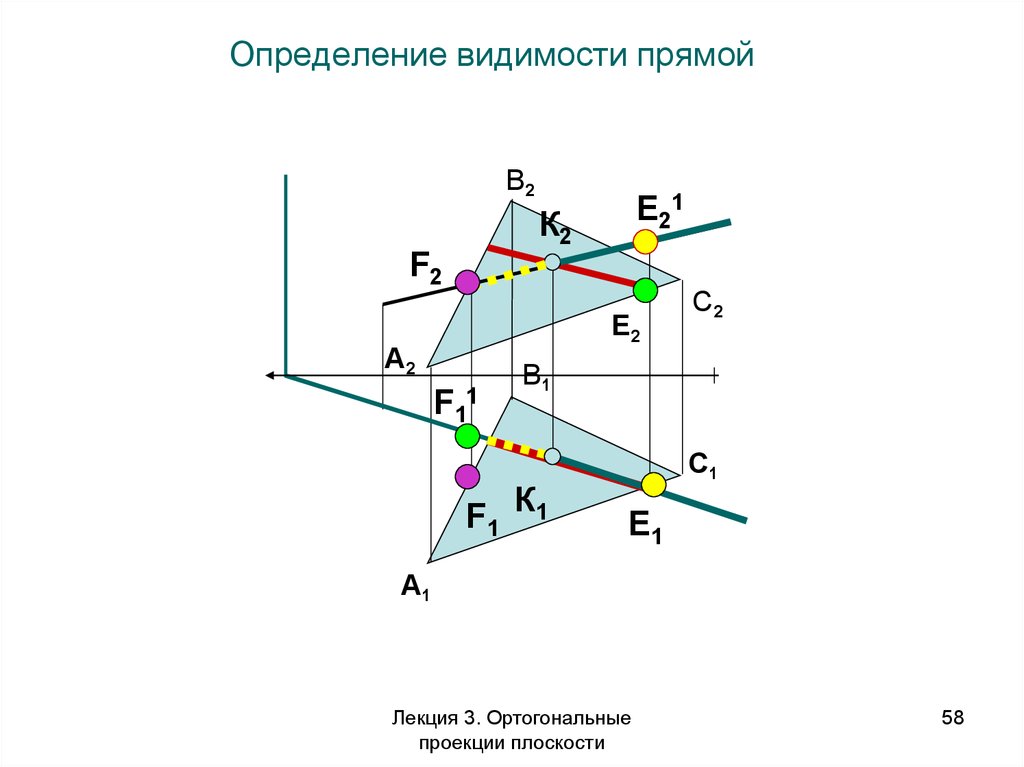
58.

Определение видимости прямой
B2
Е21
К2
F2
Е2
A2
F11
С2
B1
F1 К1
C1
E1
A1
Лекция 3. Ортогональные
проекции плоскости
58

59.

1. Плоскости пересекаются, если у них
есть общие точки
2. Плоскости пересекаются по прямой
линии, которая проходит через две
общие точки плоскостей
Лекция 3. Ортогональные
проекции плоскости
59

60.

B2
αп2
F2
К2
C2
X
αп1
A2
B1
O
F1
К1
C1
A1
• Линия пересечения фронтально-проецирующей
плоскости и плоскости общего положения определяется по точкам пересечения сторон треугольника
ΔАВС и фронтального следа плоскости α
Лекция 3. Ортогональные
проекции плоскости
60

61. Список рекомендованной литературы

• Бударин О. С. Начертательная геометрия. Краткий курс: учеб.
пособие для студентов вузов, обучающихся по направлениям в
обл. техники и технологий / О. С. Бударин. - 2-е изд., испр. Санкт-Петербург ; Москва ; Краснодар: Лань, 2009. - 368 с.: ил
• Королев Ю. И. Начертательная геометрия: учеб. для вузов
инженер.-техн. специальностей / Ю. И. Королев. - 2-е изд. Москва ; Санкт-Петербург ; Нижний Новгород [и др.]: Питер,
2010. - 256 с.: ил
• Чекмарев А. А. Начертательная геометрия и черчение: учеб.
для студентов вузов, обучающихся по техн. специальностям / А.
А. Чекмарев. - 3-е изд., перераб. и доп. - Москва: Юрайт, 2011. 471 с.: ил
Лекция 3. Ортогональные
проекции плоскости
61

62. Благодарю за внимание

Лекция 3. Ортогональные
проекции плоскости
62