Similar presentations:
Проекции точки, прямой, плоскости
1. Тема 2
Проекции точки, прямой,плоскости
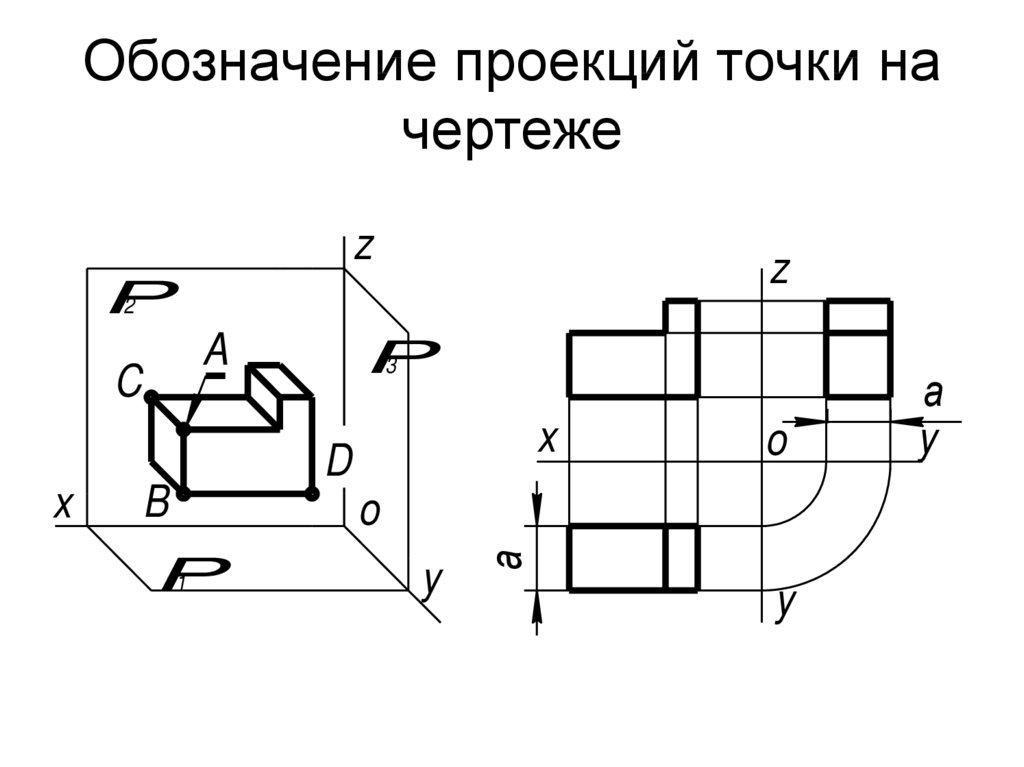
2. Обозначение проекций точки на чертеже
zz
P
2
A
C
P
3
x
D
B
P
1
o
y
а
x
o
y
а
y
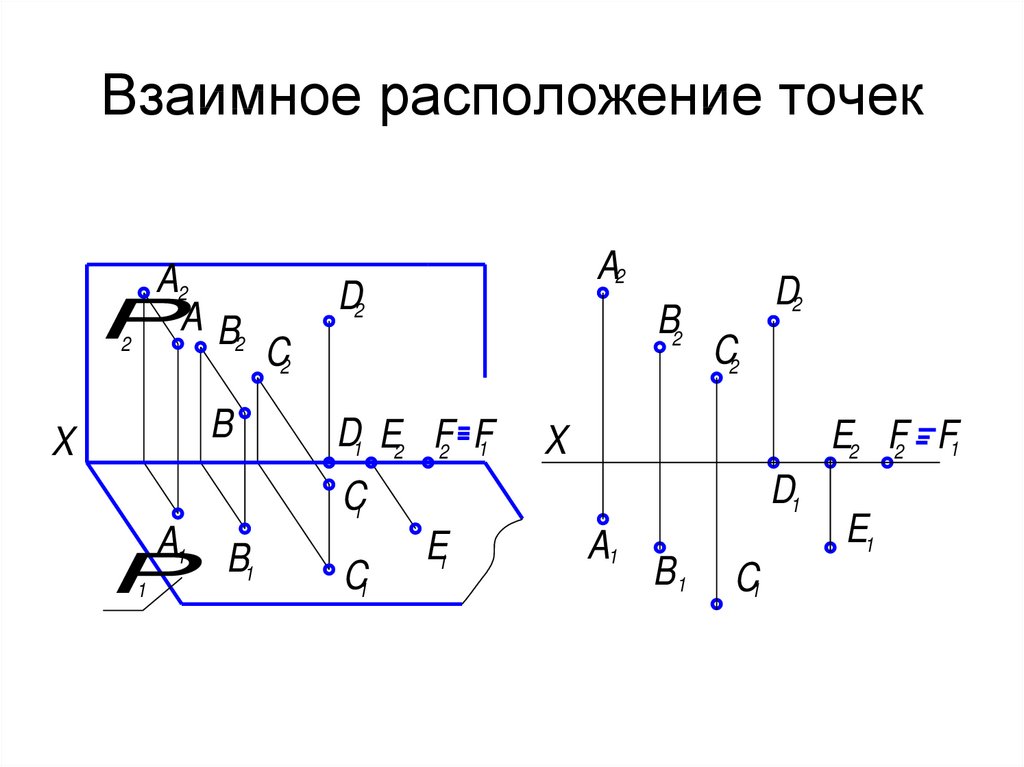
3. Взаимное расположение точек
A2AB
P
2
2
B
X
A2
D2
B2
C2
D1 E2 F2 F1
D2
C2
E2 F2 F1
X
D1
C1
A1
P
1
B1
C1
E1
A1
B1
C1
E1
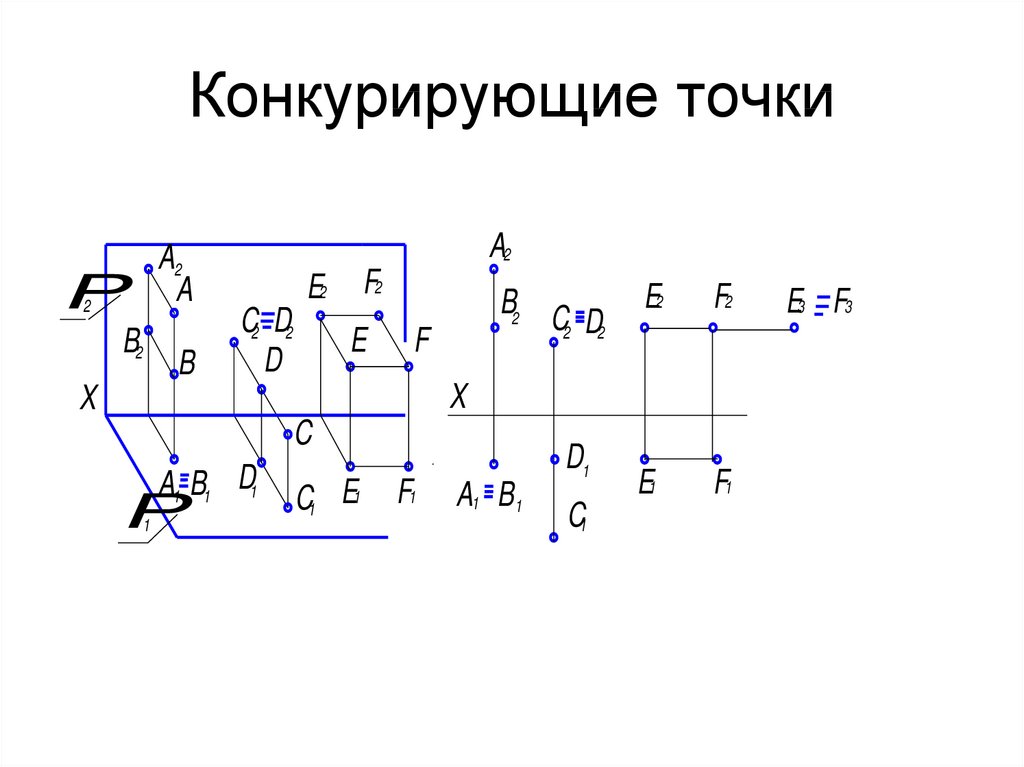
4. Конкурирующие точки
A2A
P
2
B2
B
A2
F2
E2
C2 D2
D
E
B2 C
2 D2
F
E2
F2
E1
F1
X
X
C
A1 B1 D1
P
1
C1 E1
F1
D1
A1 B 1
C1
E3 F3
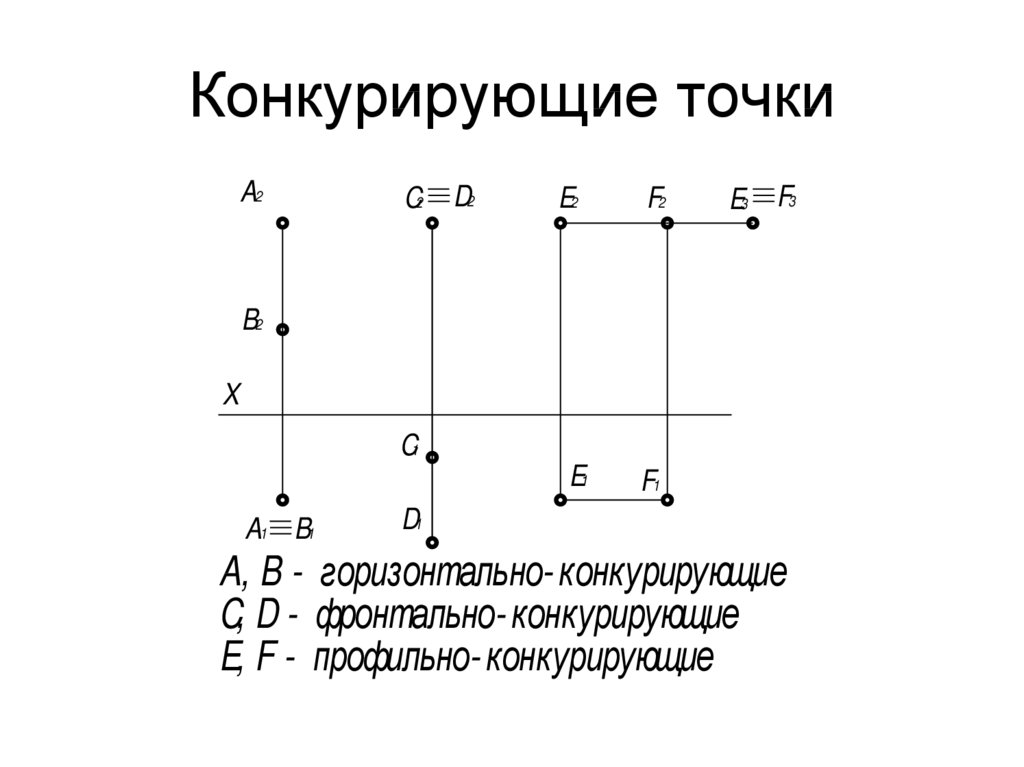
5. Конкурирующие точки
A2C2
D2
E2
F2
E3 F3
B2
X
C1
E1
A1 B1
F1
D1
A, B - горизонтально- конкурирующие
C, D - фронтально- конкурирующие
E, F - профильно- конкурирующие
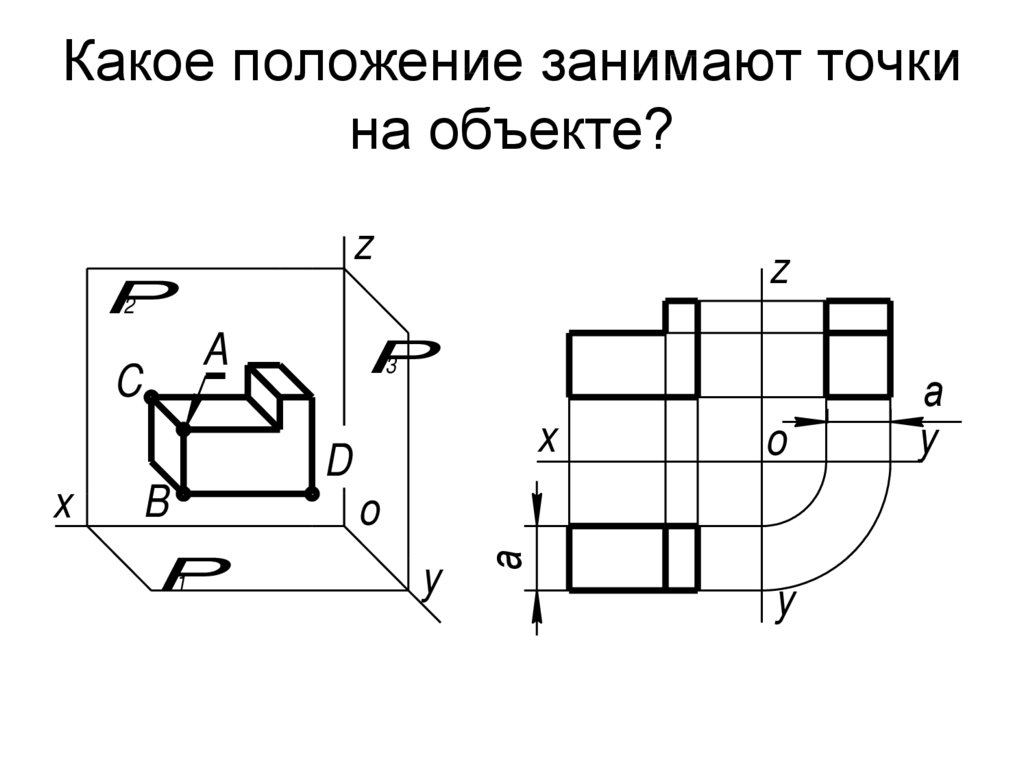
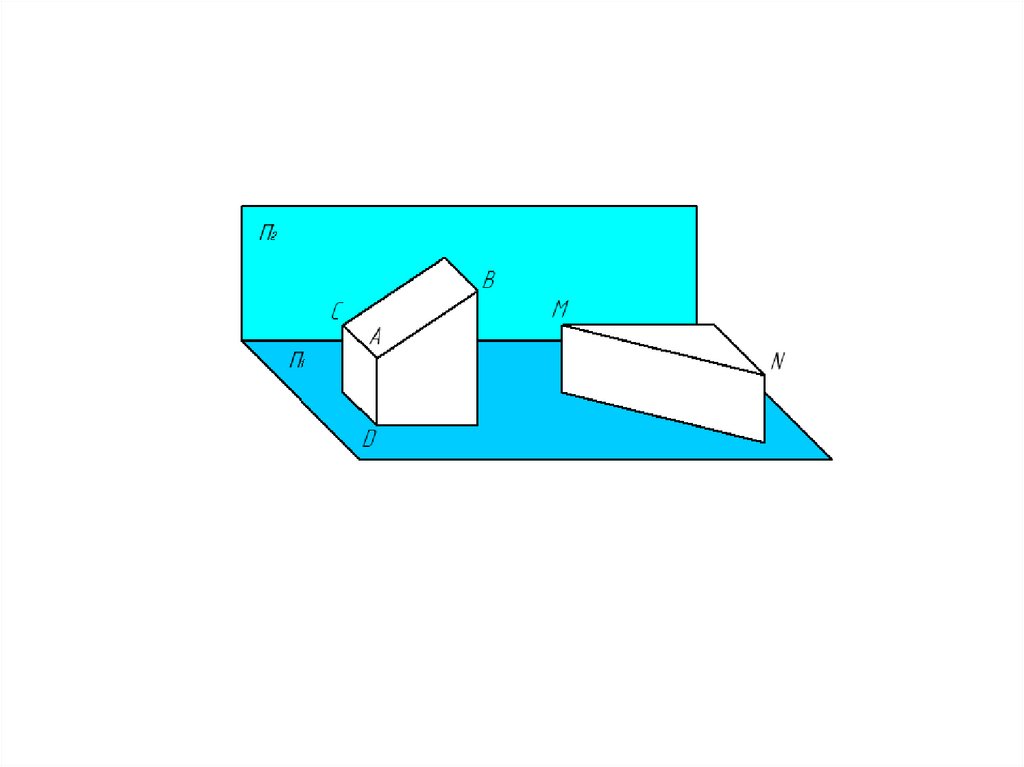
6. Какое положение занимают точки на объекте?
zz
P
2
A
C
P
3
x
D
B
P
1
o
y
а
x
o
y
а
y
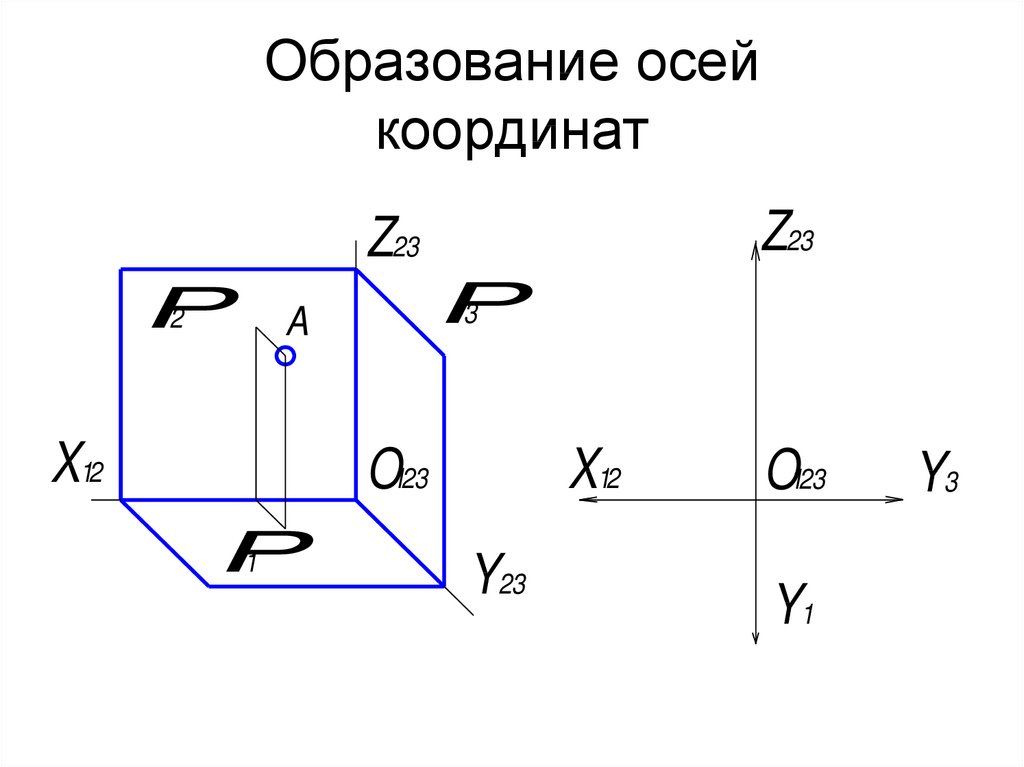
7. Образование осей координат
Z23Z23
P
2
P
3
A
X12
X12
O123
P
1
Y23
O123
Y1
Y3
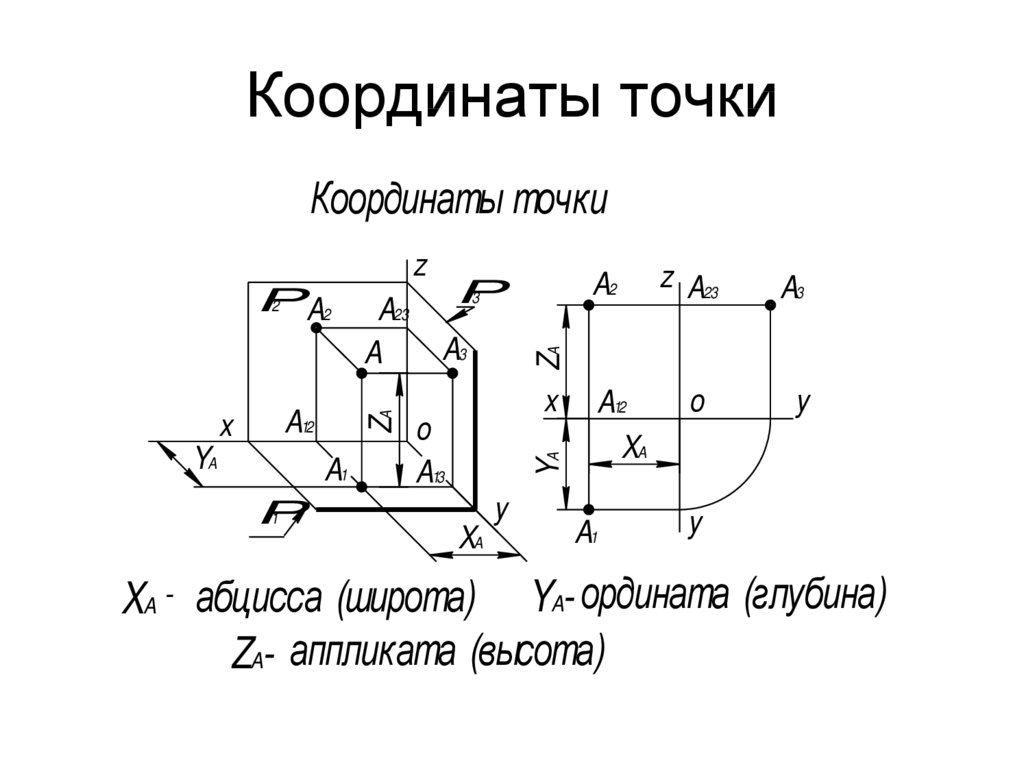
8. Координаты точки
Координаты точкиz
A12
YA
ZA
x
A1
P
1
A3
x
o
A13
y
XA
z A23
A3
ZA
A23
A
YA
P
2
A2
A2
P
3
A12
XA
A1
o
y
y
XA - абцисса (широта) YA- ордината (глубина)
ZA- аппликата (высота)
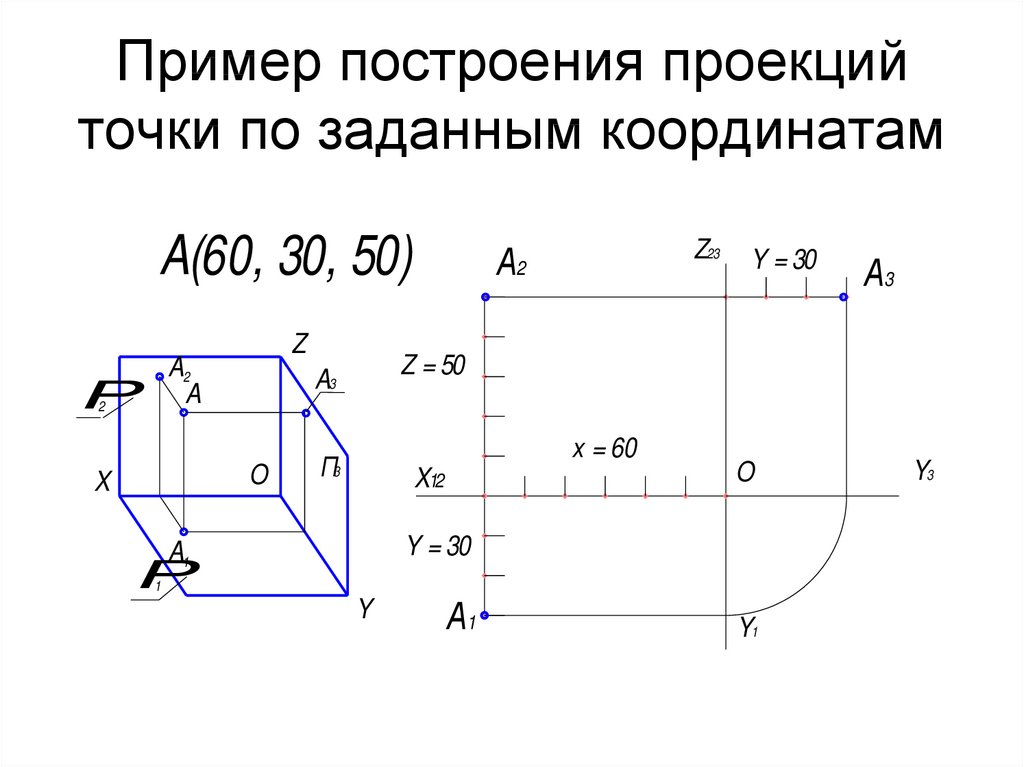
9. Пример построения проекций точки по заданным координатам
A(60, 30, 50)Z
A2
A
P
2
Y = 30
А3
Z = 50
A3
O
X
Z23
А2
x = 60
П3
X12
O
Y = 30
A1
P
1
Y
А1
Y1
Y3
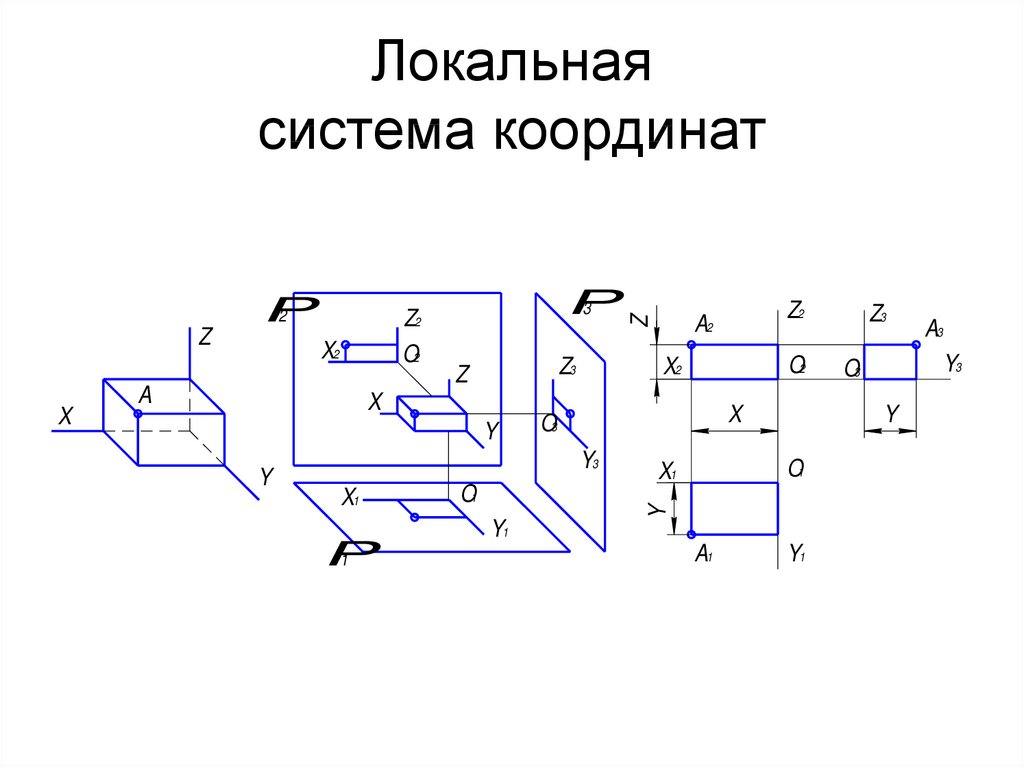
10. Локальная система координат
XX2
A
P
3
Z3
Z
X
Y
Y
O1
O2
X2
X
O3
Y3
X1
Z2
A2
Z
Z2
O2
O1
X1
Y1
P
1
A1
Z3
Y1
A3
Y3
O3
Y
Y
Z
P
2
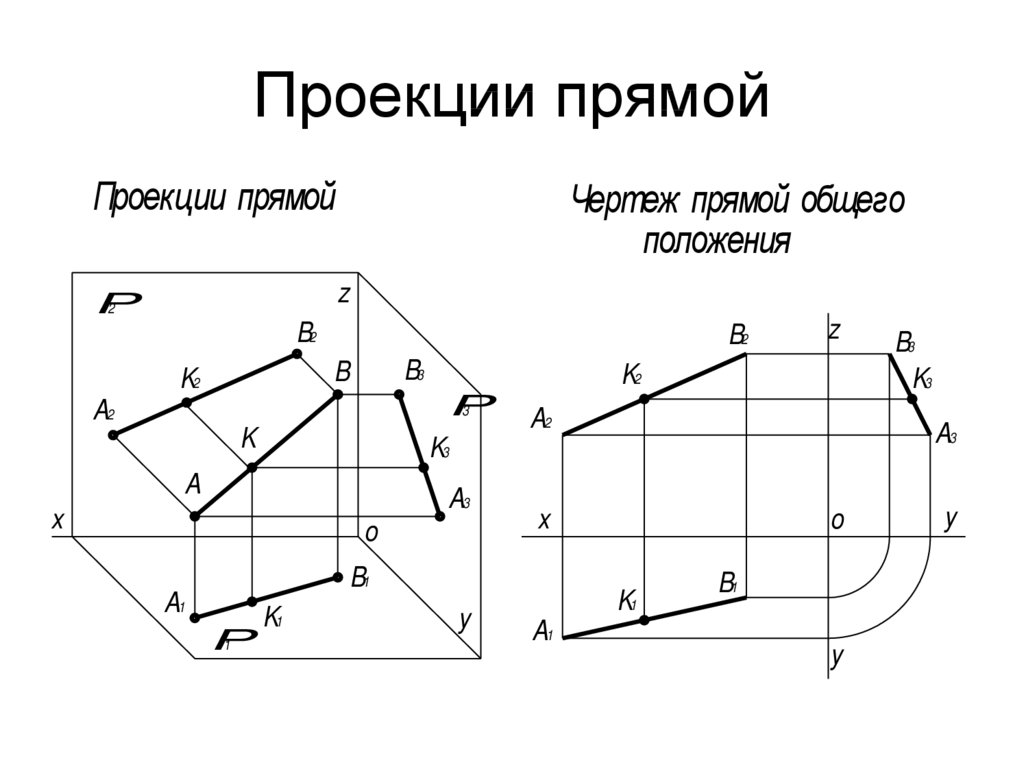
11. Проекции прямой
Проекции прямойЧертеж прямой общего
положения
z
P
2
B2
B2
B3
B
K2
K2
P
3
A2
K
A2
A3
x
o
x
B1
P
1
K1
y
o
K1
A1
B3
K3
A3
K3
A
A1
z
B1
y
y
12.
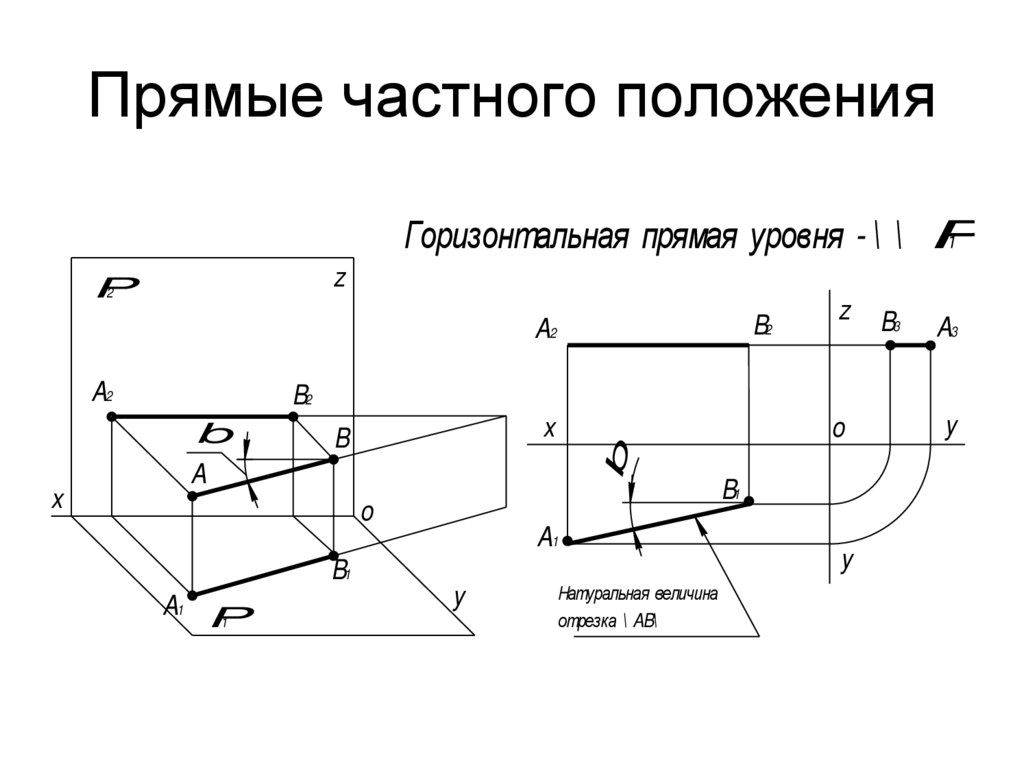
13. Прямые частного положения
Горизонтальная прямая уровня - \ \ P1
z
P
2
B2
A2
A2
x
z
B3
A3
B2
x
B
o
b
b
A
o
A1
B1
A1 P
1
y
B1
y
Натуральная величина
отрезка \ AB\
y
14.
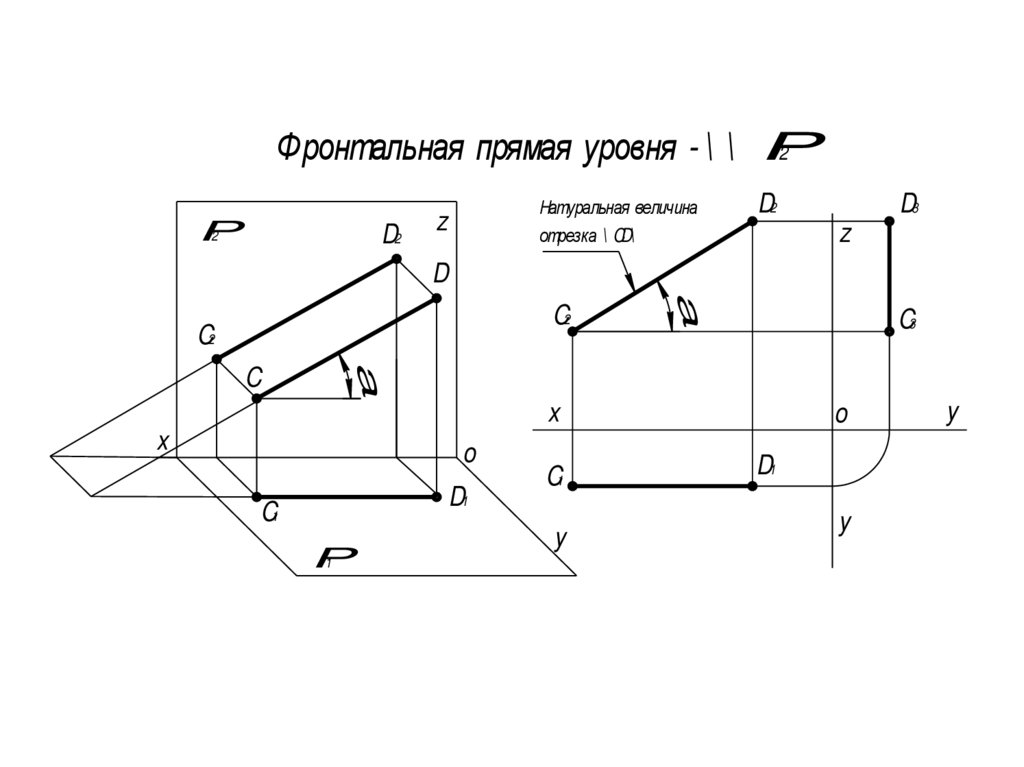
Ф ронтальная прямая уровня - \ \ P2
P
2
D2
Натуральная величина
отрезка \ CD\
z
D2
D3
z
D
C3
a
C
a
C2
C2
x
x
o
D1
C1
P
1
C1
y
o
D1
y
y
15.
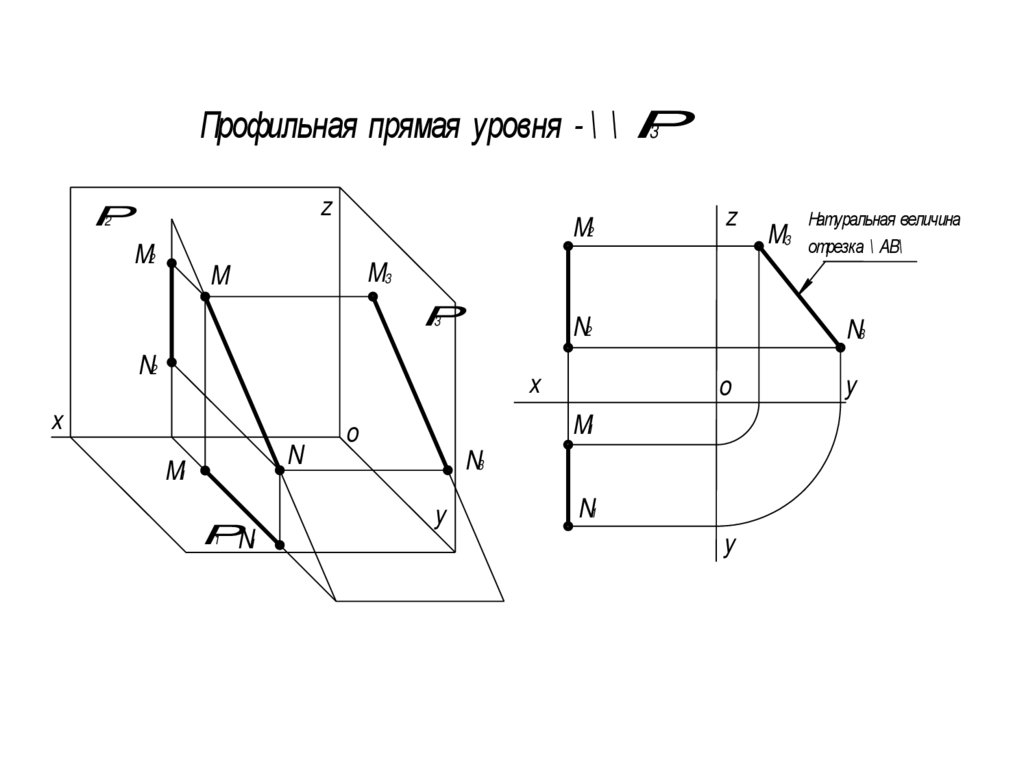
Профильная прямая уровня - \ \ P3
z
P
2
M2
M2
P
3
N2
N2
x
x
N
P
1 N1
M3
Натуральная величина
отрезка \ AB\
M3
M
M1
z
N3
o
M1
o
N3
y
N1
y
y
16.
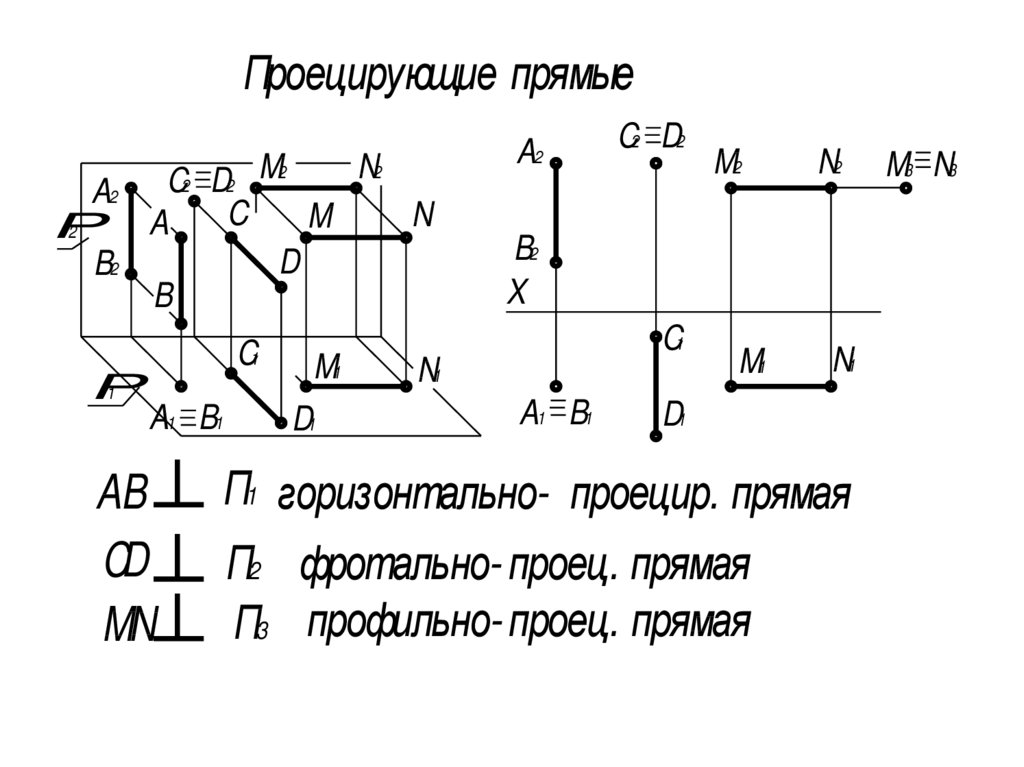
Проецирующие прямыеA2
P
2
B2
N2
C2 D2 M2
C
N
M
A
D
B
C1
P
1
A1 B1
AB
CD
MN
M1
D1
A2
C2 D2
M2
N2
B2
X
C1
N1
A1 B1
M1
N1
D1
П1 горизонтально- проецир. прямая
П2 фротально- проец. прямая
П3 профильно- проец. прямая
M3 N3
17.
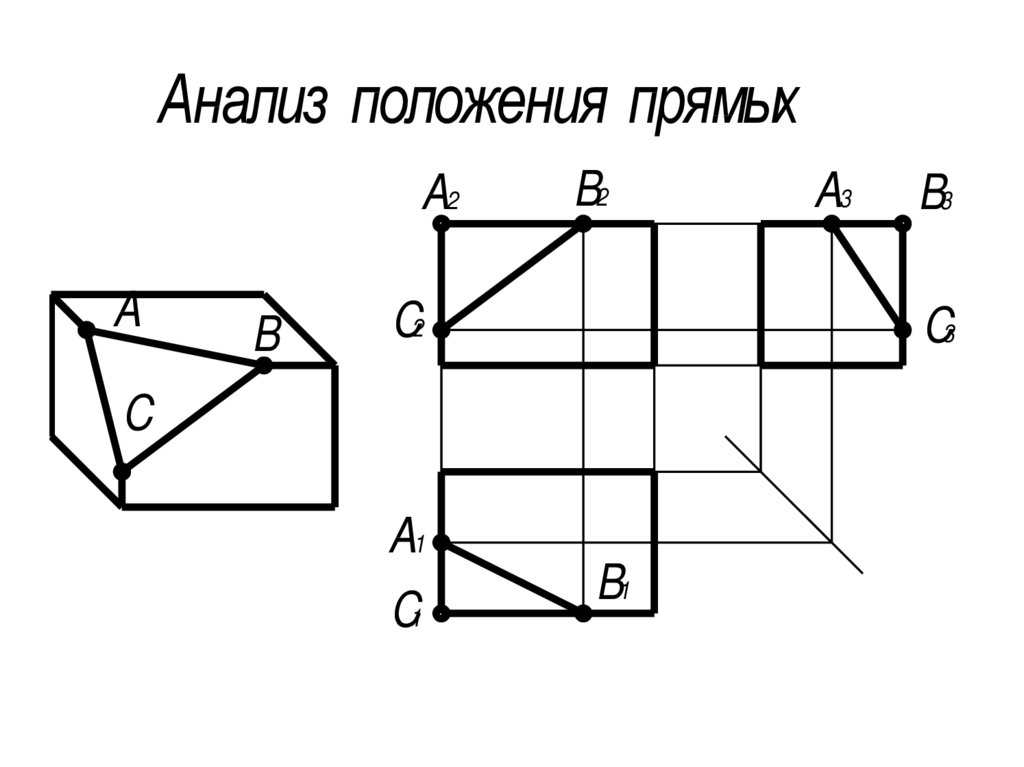
Анализ положения прямыхA2
A
B
B2
C2
B3
C3
C
A1
C1
A3
B1
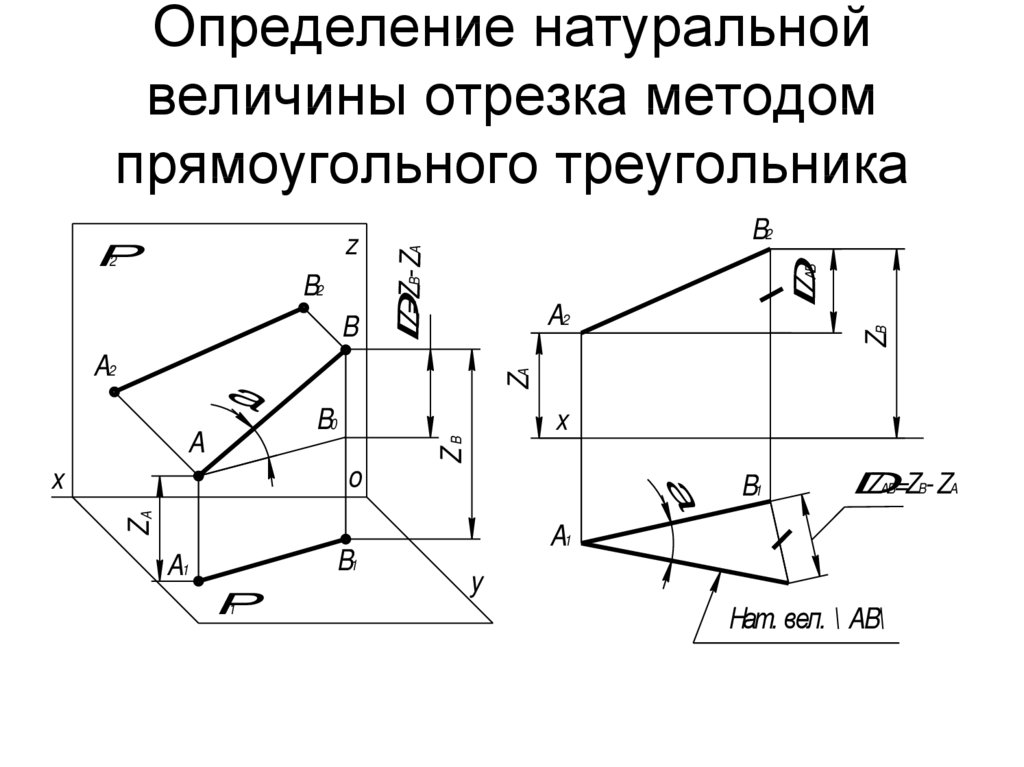
18. Определение натуральной величины отрезка методом прямоугольного треугольника
A2A2
ZA
B
a
B0
x
ZB
A
ZB
B2
D
ZAB
2
P
B2
D
Z= ZB- ZA
z
ZA
a
o
x
B1
A1
1
P
B1
ZAB=ZB- ZA
D
A1
y
Нат. вел. \ AB\
19. Метод прямоугольного треугольника
• Натуральная величина отрезка равнагипотенузе прямоугольного
треугольника, у которого один катет
равен любой проекции отрезка, а
второй – разности «недостающих»
координат.
20.
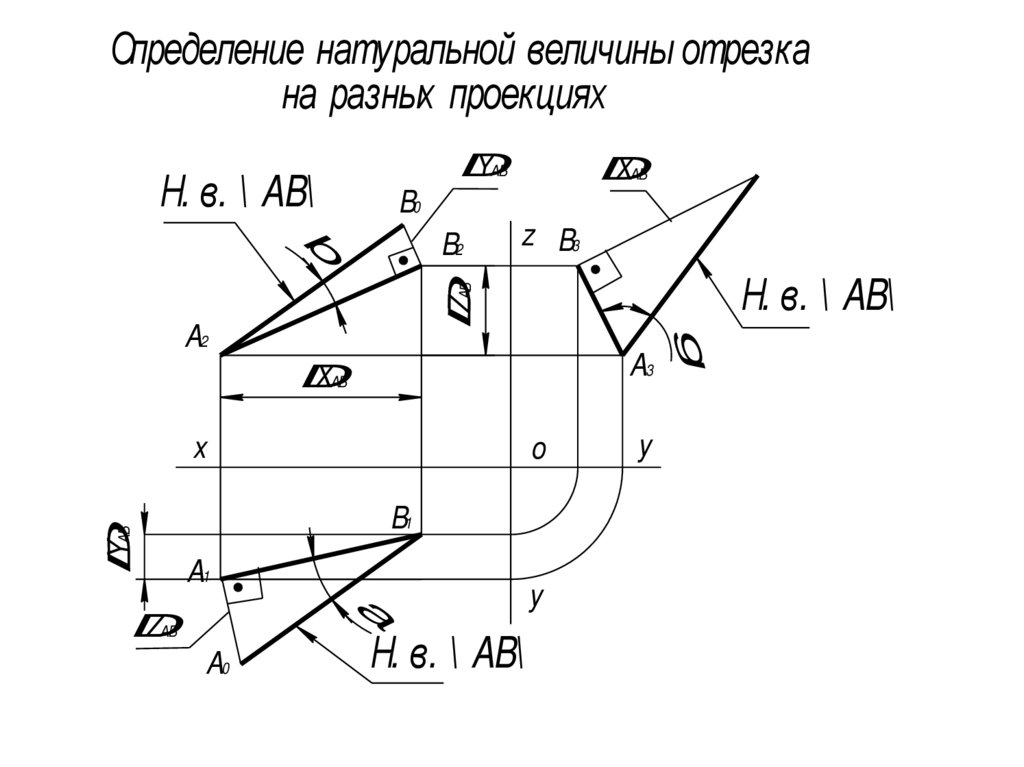
Определение натуральной величины отрезкана разных проекциях
D
YAB
Н. в. \ AB\
D
XAB
B0
b
z B3
Н. в. \ AB\
A2
A3
D
XAB
YAB
D
x
o
B1
A1
D
ZAB
A0
a
Н. в. \ AB\
y
y
g
D
ZAB
B2
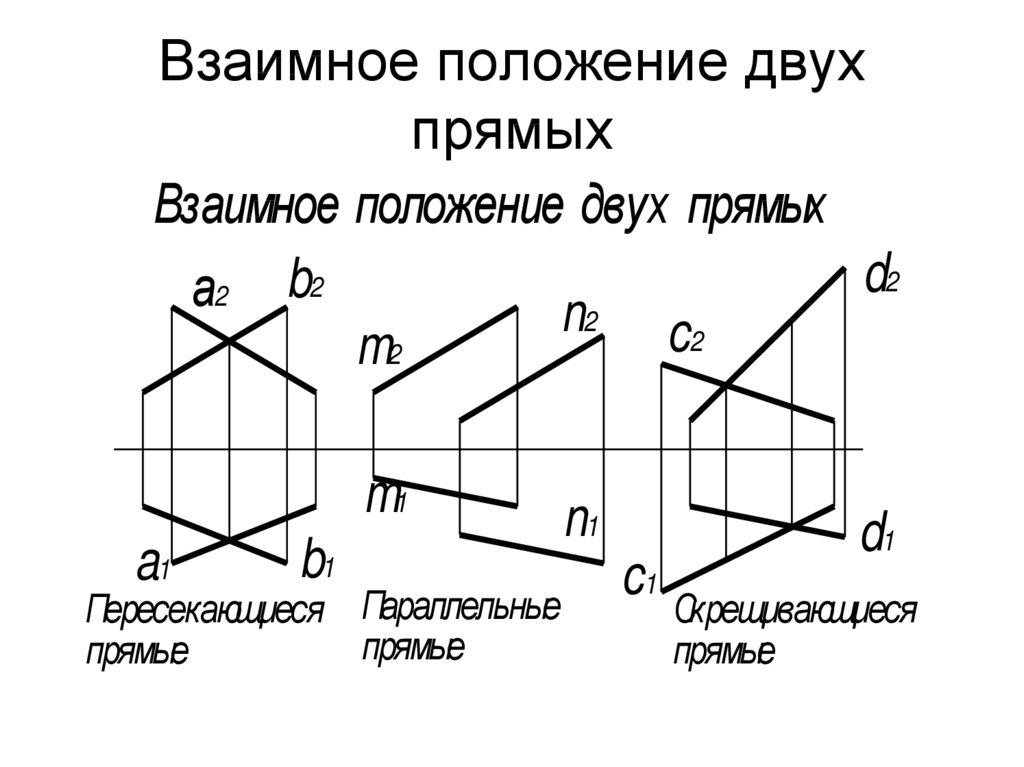
21. Взаимное положение двух прямых
Взаимное положение двух прямыхd2
а2 b2
n2 c2
m2
m1
a1
b1
Пересекающиеся Параллельные
прямые
прямые
n1
c1
d1
Скрещивающиеся
прямые
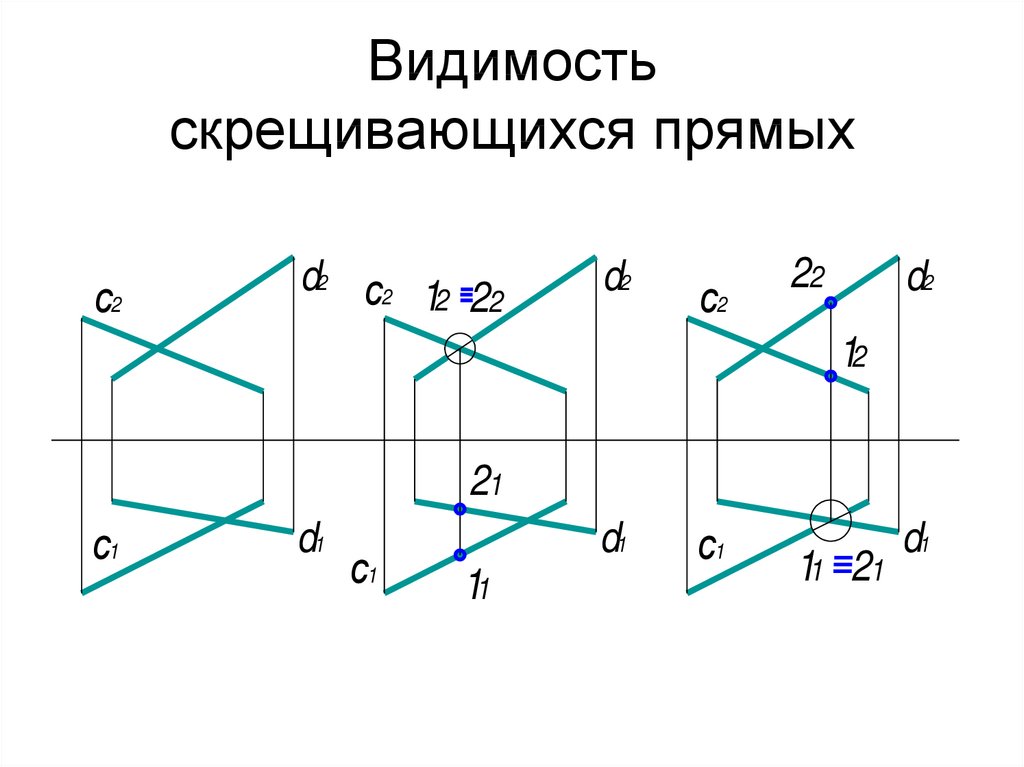
22. Видимость скрещивающихся прямых
с2d2 с2 12
22
d2
с2
22
d2
12
21
с1
d1
с1
d1
11
с1
11 21
d1
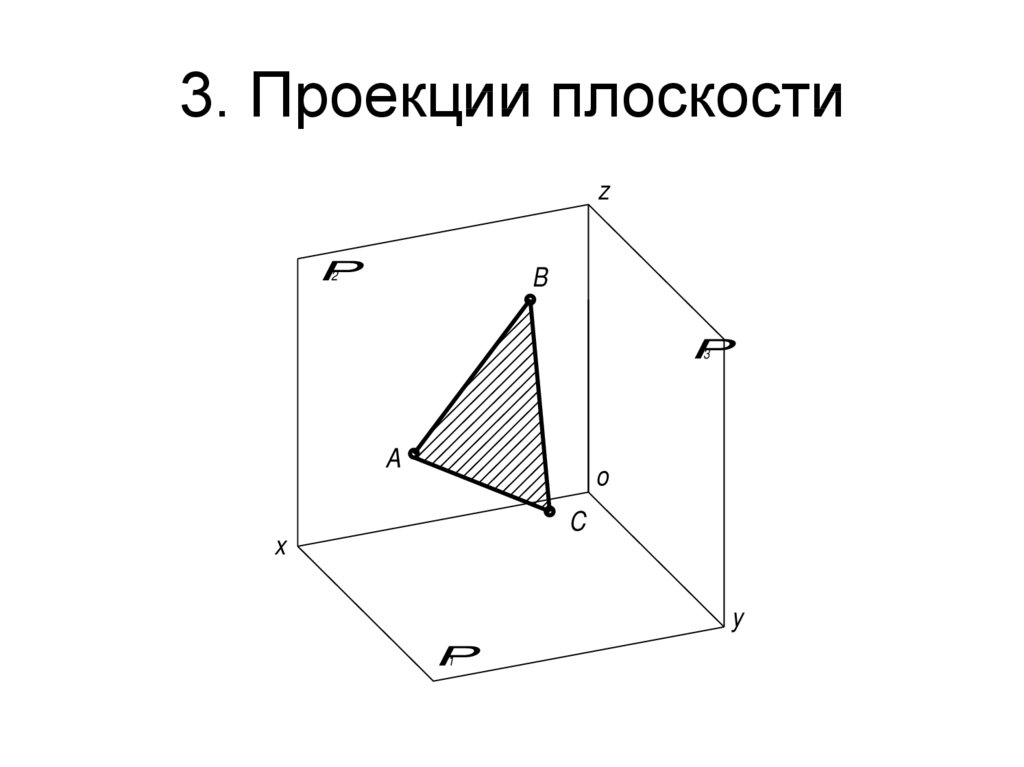
23. 3. Проекции плоскости
zP
2
B
P
3
A
o
C
x
y
P
1
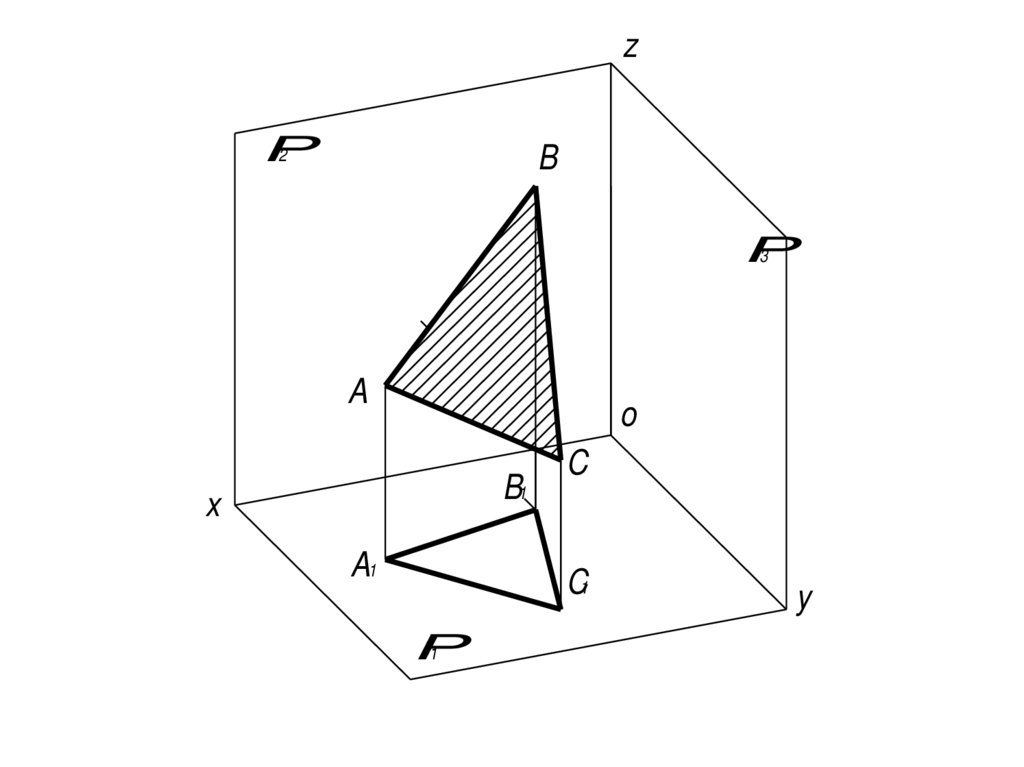
24.
zP
2
B
P
3
A
o
B1
x
A1
C
C1
P
1
y
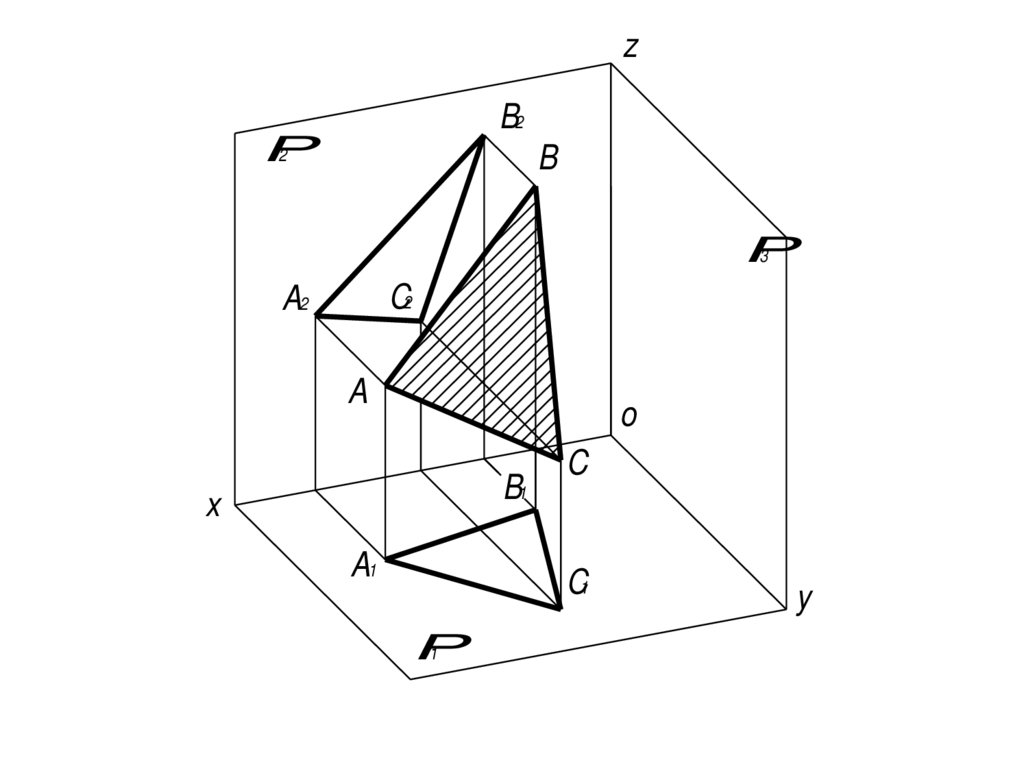
25.
zB2
P
2
B
P
3
C2
A2
A
o
B1
x
A1
C
C1
P
1
y
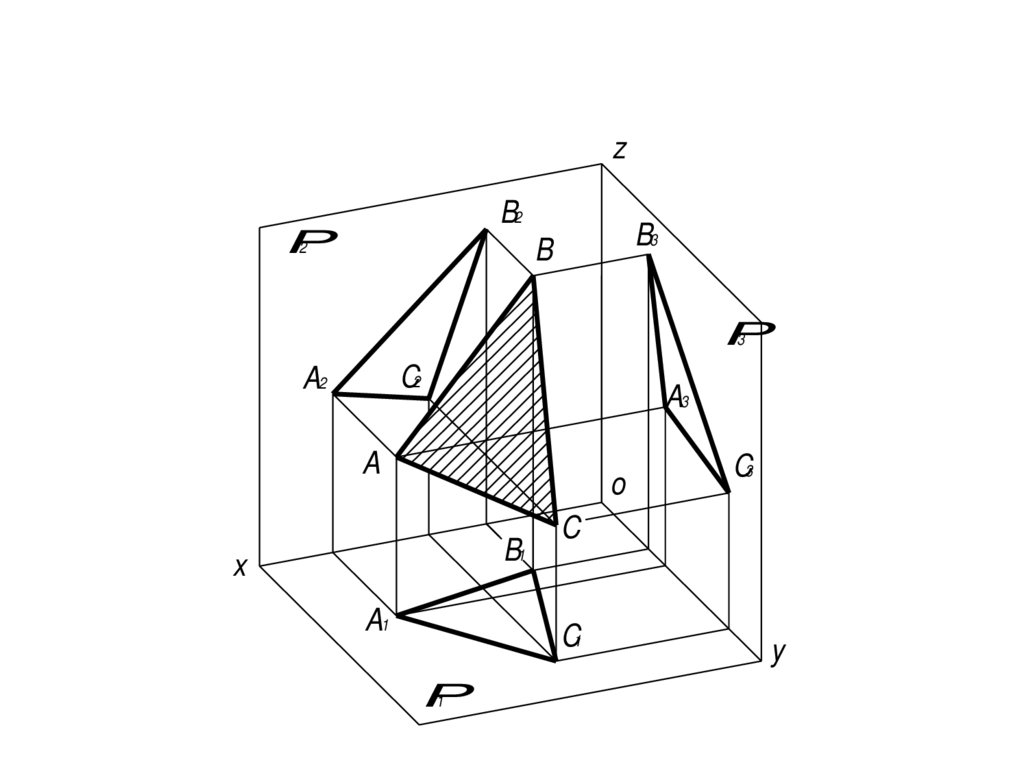
26.
zB2
P
2
B3
B
P
3
C2
A2
A3
A
o
B1
x
A1
C
C1
P
1
C3
y
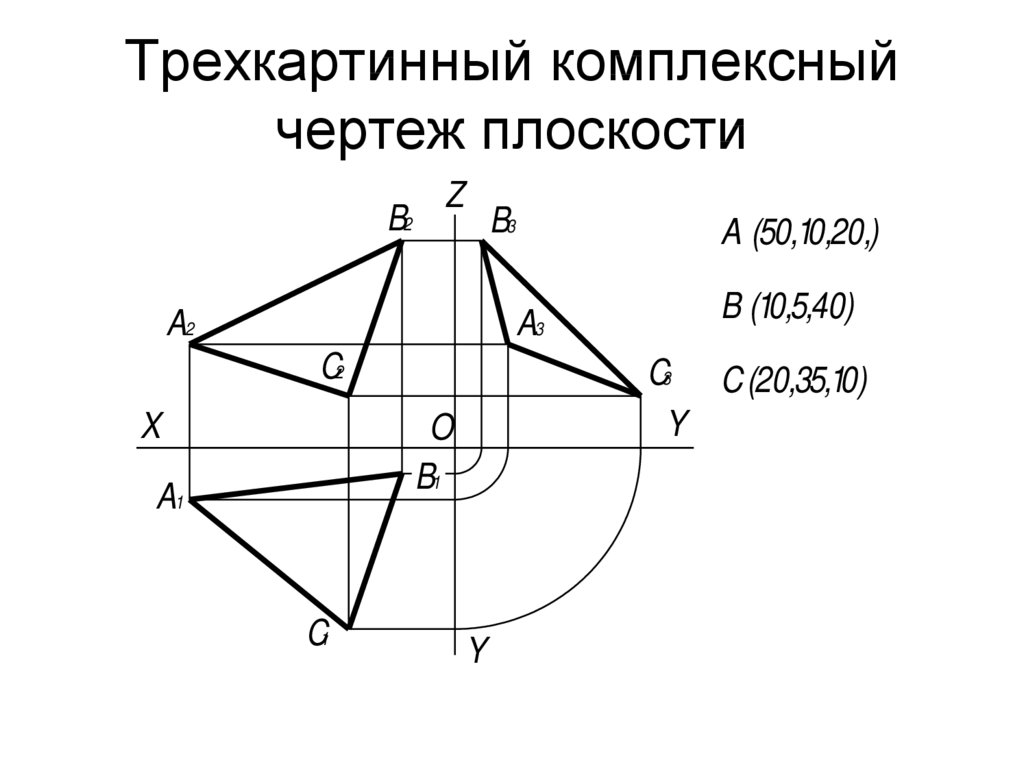
27. Трехкартинный комплексный чертеж плоскости
B2Z
B3
A2
A (50,10,20,)
A3
C2
X
C3 C (20,35,10)
Y
O
B1
A1
C1
B (10,5,40)
Y
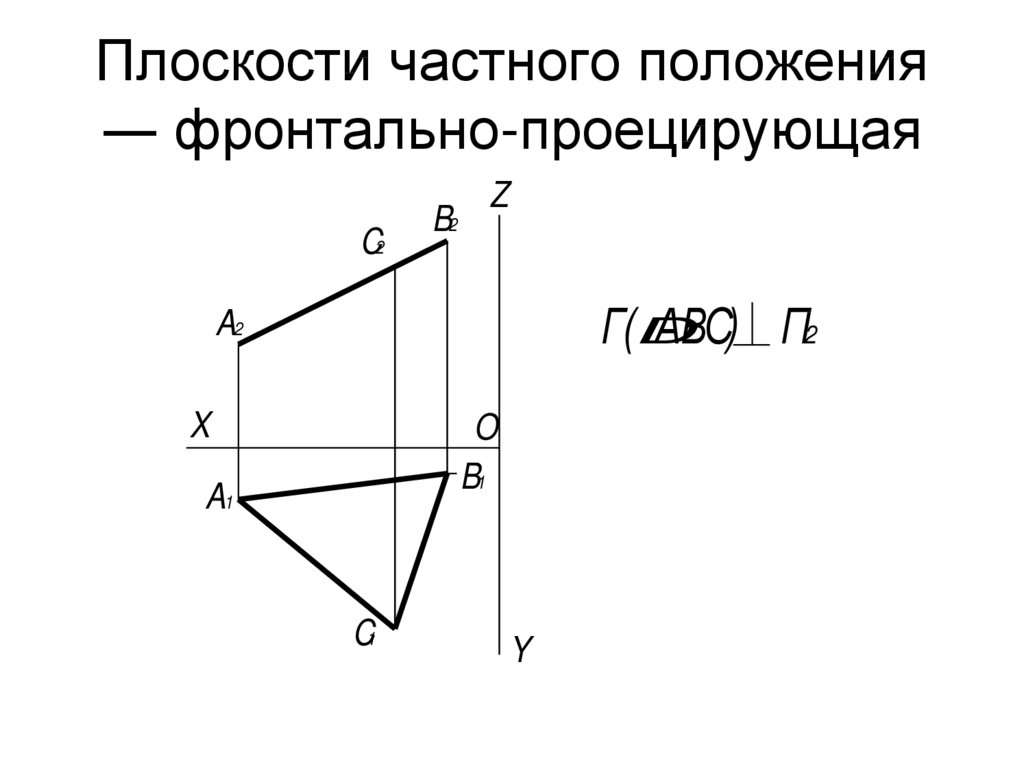
28. Плоскости частного положения ― фронтально-проецирующая
C2B2
Z
Г(D
АВС) П2
A2
X
O
B1
A1
C1
Y
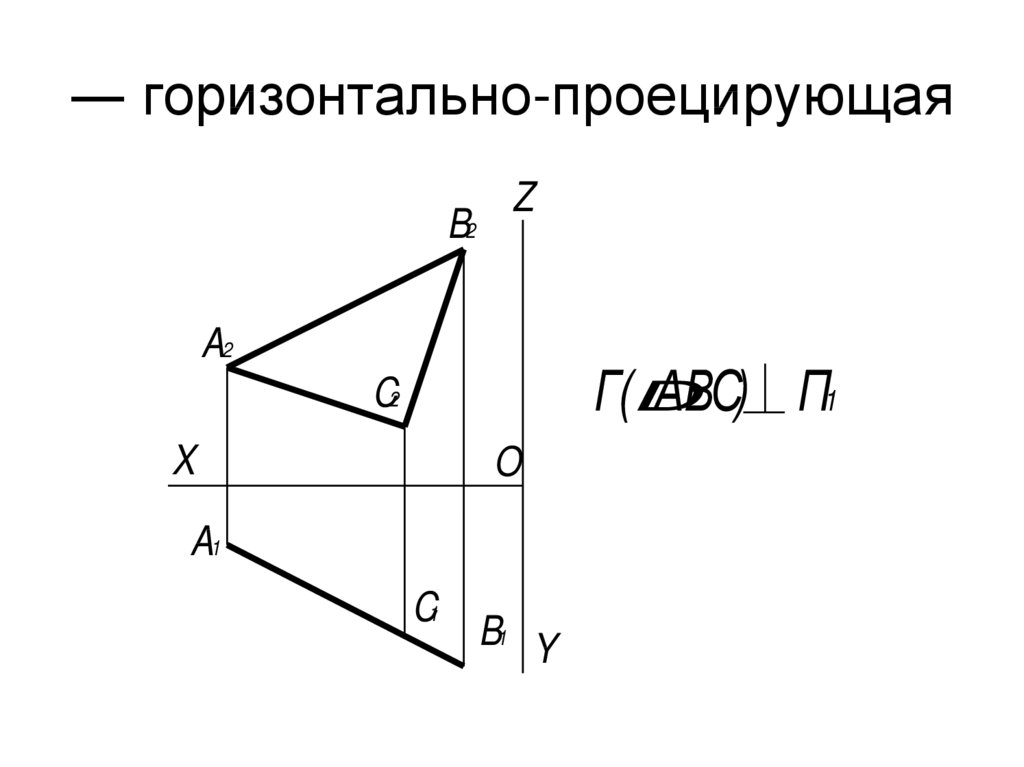
29. ― горизонтально-проецирующая
B2Z
A2
Г(D
АВС) П1
C2
X
O
A1
C1
B1 Y
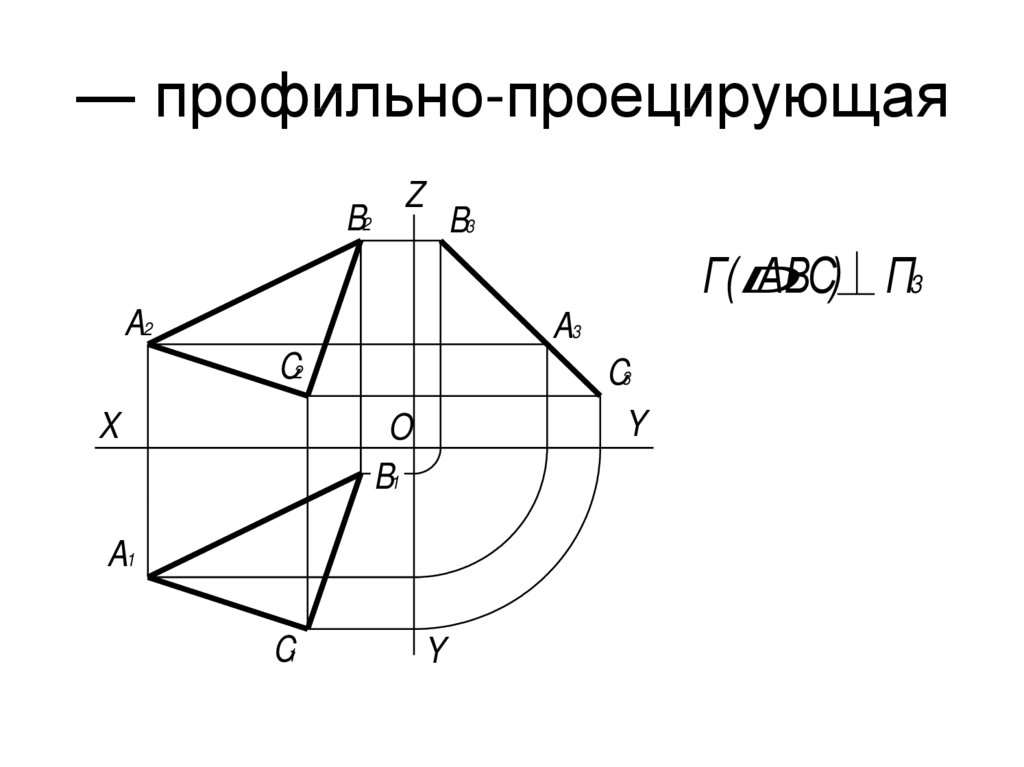
30. ― профильно-проецирующая
B2Z
B3
Г(D
АВС) П3
A2
A3
C2
X
C3
Y
O
B1
A1
C1
Y
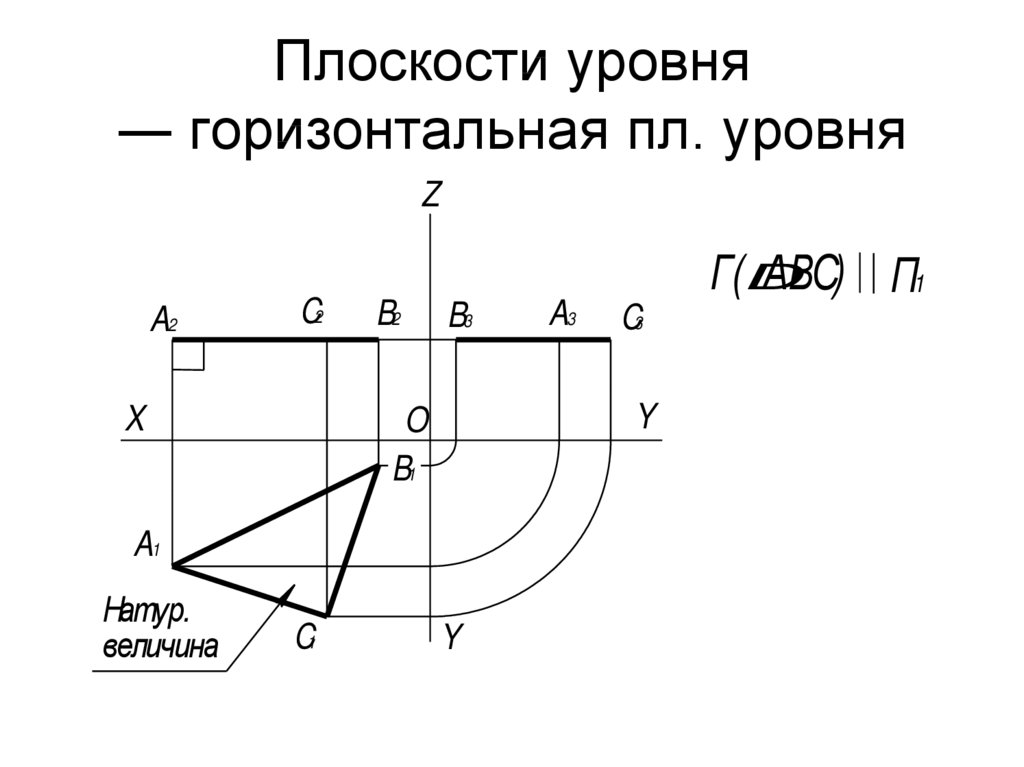
31. Плоскости уровня ― горизонтальная пл. уровня
ZA2
C2
X
B2
B3
C1
C3
Y
O
B1
A1
Натур.
величина
A3
Г(D
АВС) П1
Y
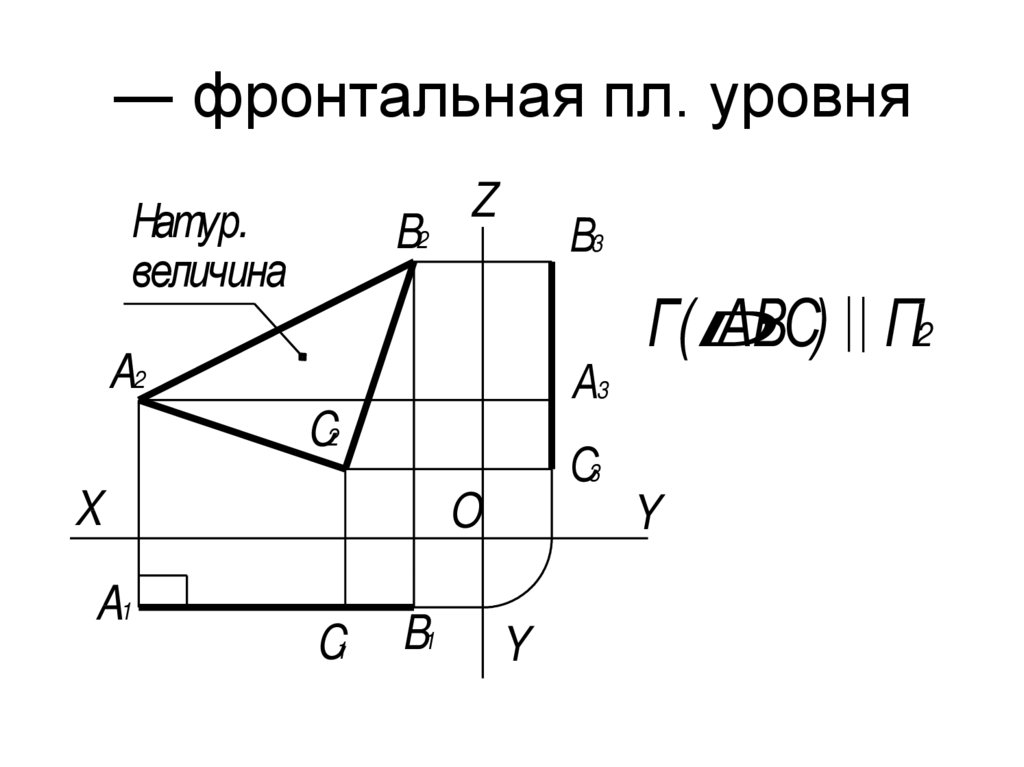
32. ― фронтальная пл. уровня
Натур.величина
B2
Z
В3
A2
А3
C2
С3
X
A1
O
C1
Г(D
АВС) П2
B1
Y
Y
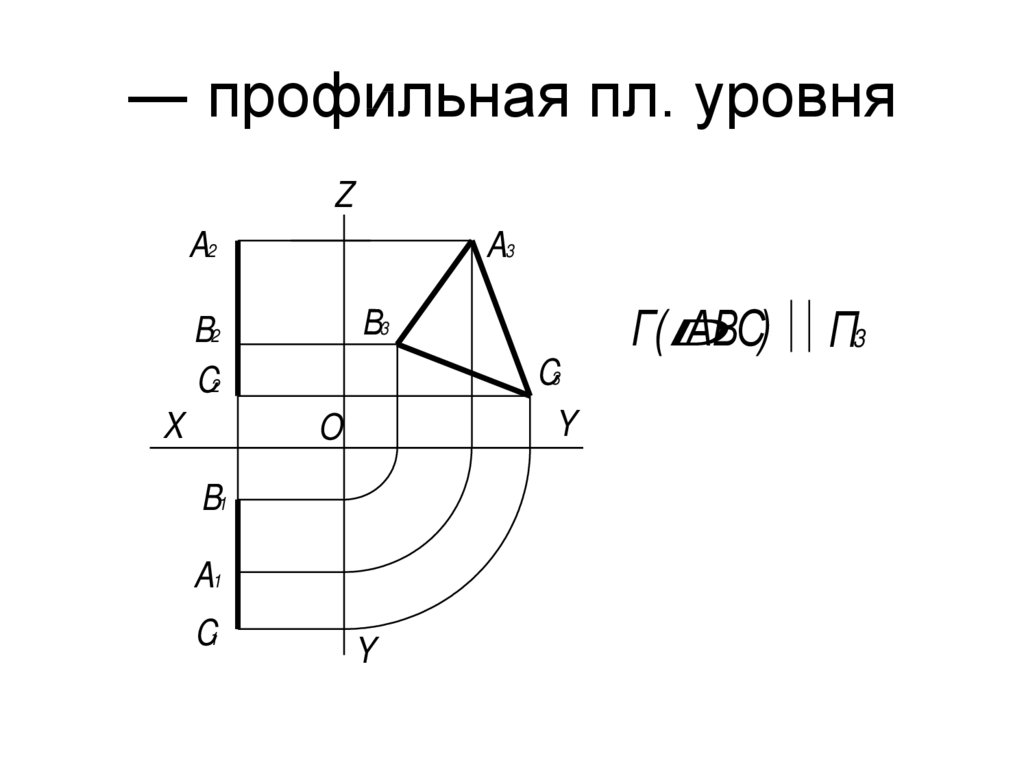
33. ― профильная пл. уровня
ZA2
A3
X
C3
Y
O
B1
A1
C1
Г(D
АВС)
В3
B2
C2
Y
П3
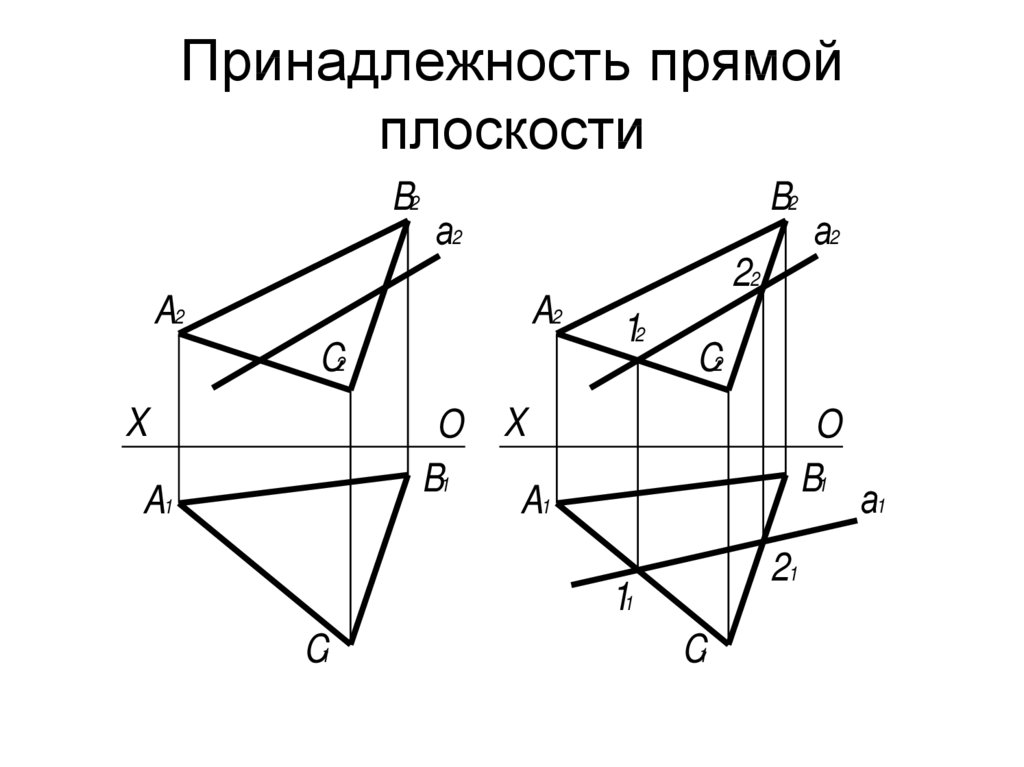
34. Принадлежность прямой плоскости
B2B2
а2
а2
22
A2
A2
C2
X
O
B1
A1
12
C2
X
O
B1
A1
21
11
C1
C1
а1
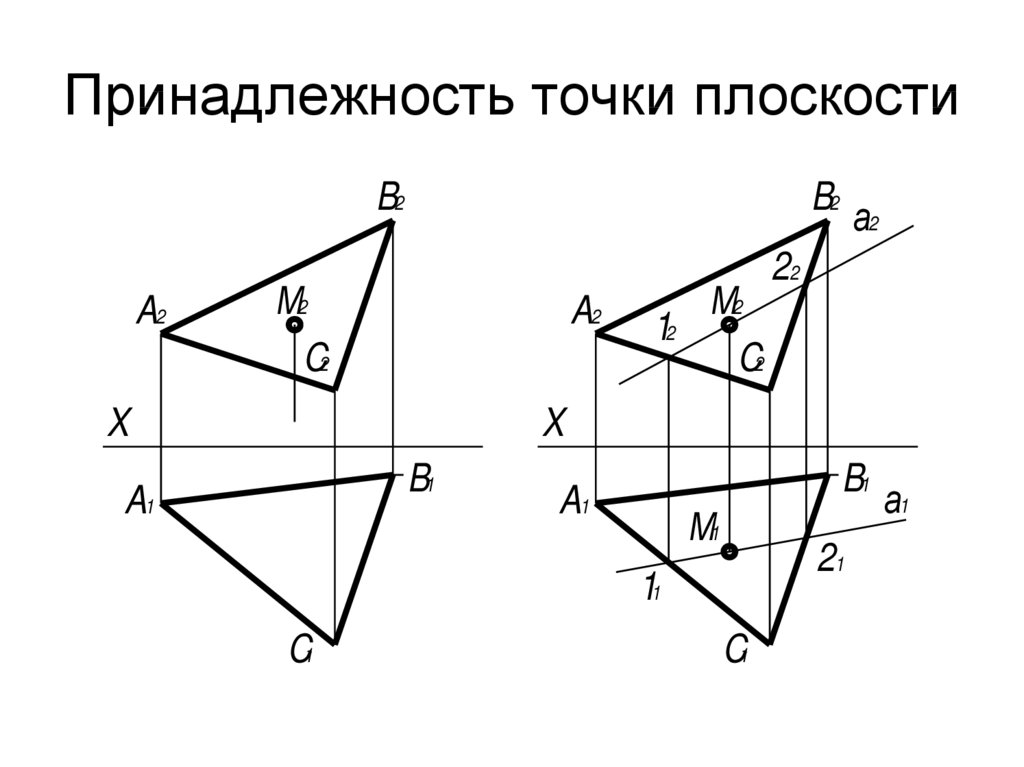
35. Принадлежность точки плоскости
B2A2
B2
М2
C2
A2
X
М2
12
C2
а2
22
X
B1
A1
B1
A1
М1
21
11
C1
C1
а1
36. Пример построения фигуры, принадлежащей плоскости
B2A2
X
B2
К2 L2
N2
A2
M2
N2
32
C2
M2
22
42
C2
X
B1
A1
К2 L2
12
B1
11
A1
21
31
N1
C1
M1
41
C1




 drafting
drafting








