Кинематика

1. КИНЕМАТИКА

ЕГЭ. ФИЗИКА
РЕПЕТИЦИЯ ПО ФИЗИКЕ
Владимир Петрович Сафронов
г. Ростов-на-Дону, 2015
звоните: т. 8 928 111 7884
пишите: [email protected]

2. ЧАСТЬ 1. МЕХАНИКА

изучает закономерности механического движения.
1.1.1-2. Механическое движение — изменение взаимного расположения тел
с течением времени.
Глава 1
КИНЕМАТИКА
Материальная точка (МТ) — тело, размерами которого можно пренебречь.
Система отсчета — служит для определения положения тела в пространстве и времени.
Состоит из тела отсчета, системы координат и часов.
Y
M
y1
r
r1
y
x1, y1 — координаты МТ .
S – путь
r
r1 x12 y12 — радиус-вектор МТ .
r r r
r r2 r1 — перемещение МТ .
r
r
y2
Vx x2 x1 — проекция перемещения на ось X,
r
r2
V y y2 y1 — проекция перемещения на ось X,
x1
0
r
r r x2 y2 — модуль перемещения.
x2
x
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
X

3. СЛОЖЕНИЕ ПЕРЕМЕЩЕНИЙ

Перемещения складываются векторно.
Y
т.2
y23
y13
r
r23
r
r12
r
r
r
r13 r12 r23
т.3
x13 x12 x23
r
r13
y12
y13 y12 y23
т.1
r
r13 V r13
x12
x23
x13
X
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
x13 y13
2
2

4. СЛОЖЕНИЕ ДВИЖЕНИЙ (принцип суперпозиции движений)

(принцип суперпозиции движений)
Любое сложное движение на плоскости можно представить как сумму двух
прямолинейных независимых движений, например, вдоль осей Х и Y
Y
X
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

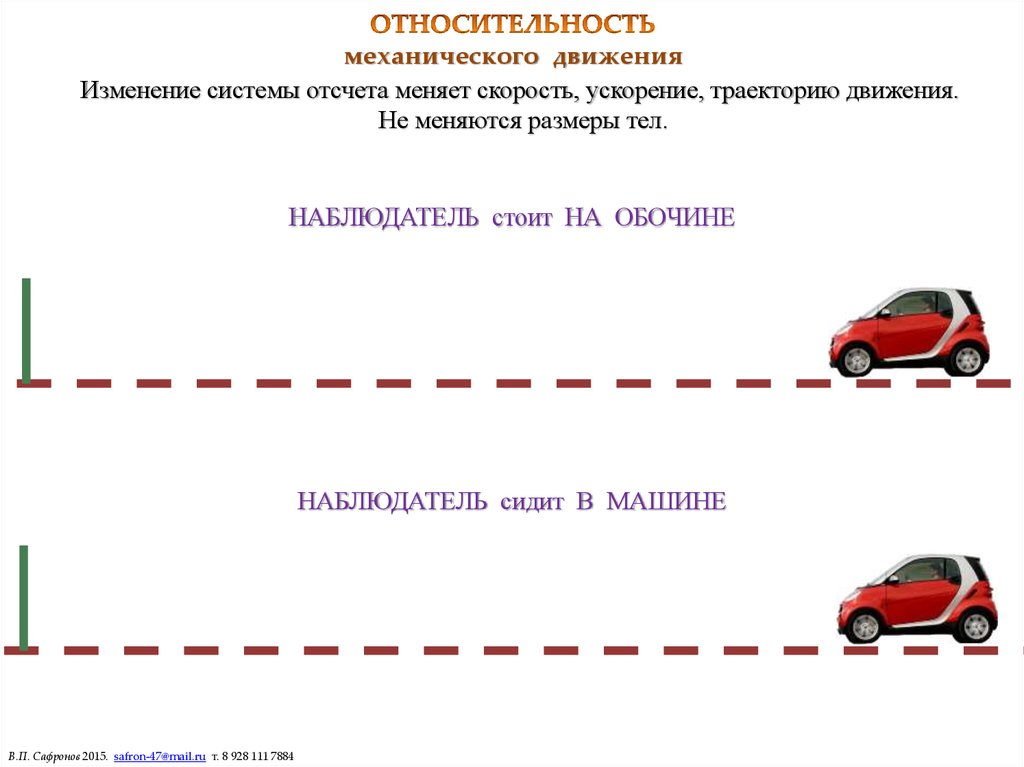
5. ОТНОСИТЕЛЬНОСТЬ механического движения

механического движения
Изменение системы отсчета меняет скорость, ускорение, траекторию движения.
Не меняются размеры тел.
НАБЛЮДАТЕЛЬ стоит НА ОБОЧИНЕ
НАБЛЮДАТЕЛЬ сидит В МАШИНЕ
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

6. ПРИМЕРЫ ПРОСТЫХ ДВИЖЕНИЙ

Кинематические уравнения движения (законы движения) позволяют найти
положение, движущейся материальной точки, в любой момент времени:
x x( t ), y y( t ).
Примеры
x ( t ) 2 2t .
1.
-6
-4
-4
-3
-2
-2
0
-1
2
0
4
1
6
2
8
3
X, м
t,c
Движение называется равномерное прямолинейное.
x ( t ) 2 2t t 2 .
2.
-6
-5
-4
-2(4)
-3
-2
-1
-1(3)
0
1
2
3
X,м
0(2)
1
t,c
Движение называется равноускоренное прямолинейное.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

7. СКОРОСТЬ

Математика
СРЕДНЕЙ СКОРОСТЬЮ изменения функции f ( t )
f
называется отношение приращения функции f f2 f1
vср
.
t
к приращению аргумента
t t 2 t1
Примеры
r
r
Vr
Средняя векторная скорость - vср
Vt
V x x x0
v
Средняя координатная скорость x ср
Vt
t
VS
Средняя путевая скорость - vср
Vt
МГНОВЕННОЙ, ИСТИННОЙ СКОРОСТЬЮ изменения функции f ( t )
называется предел, к которому стремится средняя скорость при
t 0.
Это скорость в заданный момент времени t :
f df
ft/ .
t 0 t
dt
v t lim
Таким образом, чтобы определить скорость изменения функции,
нужно взять производную этой функции по времени.
Скорость определяет быстроту изменения функции.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

8. СКОРОСТИ ДВИЖЕНИЯ

определяют быстроту движения.
При движении материальной точки радиус-вектор, координаты и путь
становятся функциями от времени:
r r ( t ), { x x ( t ), y y( t )}, S S ( t ).
Поэтому, вводится три типа скоростей:
Векторная скорость (просто скорость)
v , м/с — определяет быстроту изменения радиус-вектора и равна
Y
v
dr
rt / .
dt
Вектор скорости направлен по касательной к траектории.
v
vy
Координатные скорости
определяют быстроту изменения координат точки и
являются проекциями векторной скорости на оси X, Y.
0
vx
X
dx
dy
/
vx
xt , vy
yt/ .
dt
dt
Скалярная скорость v , м/с — это скорость изменения пути S: v
Из теоремы Пифагора
| v( t ) | v( t ) v x 2 v y 2 .
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
dS
St/ .
dt

9. СКОРОСТЬ. ПРИМЕРЫ

1. Равномерное прямолинейное движение.
x ( t ) 2 2t .
-6
-4
-4
-3
-2
-2
0
-1
2
0
4
1
6
2
8
3
X
t,c
v x x t 2 2t t 2 м/с.
2. Равнопеременное прямолинейное движение.
x ( t ) 2 2t t 2 .
-6 м/с
6 м/с
-6
-2(4)
-4 м/с
-5
-4
-3
-2
4 м/с
-1
-1(3)
v x x t 2 2t t 2
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
-2 м/с
0
t
1
2 м/с
2
0(2)
2 2t м/с.
0 м/с
3
1
X
t,c

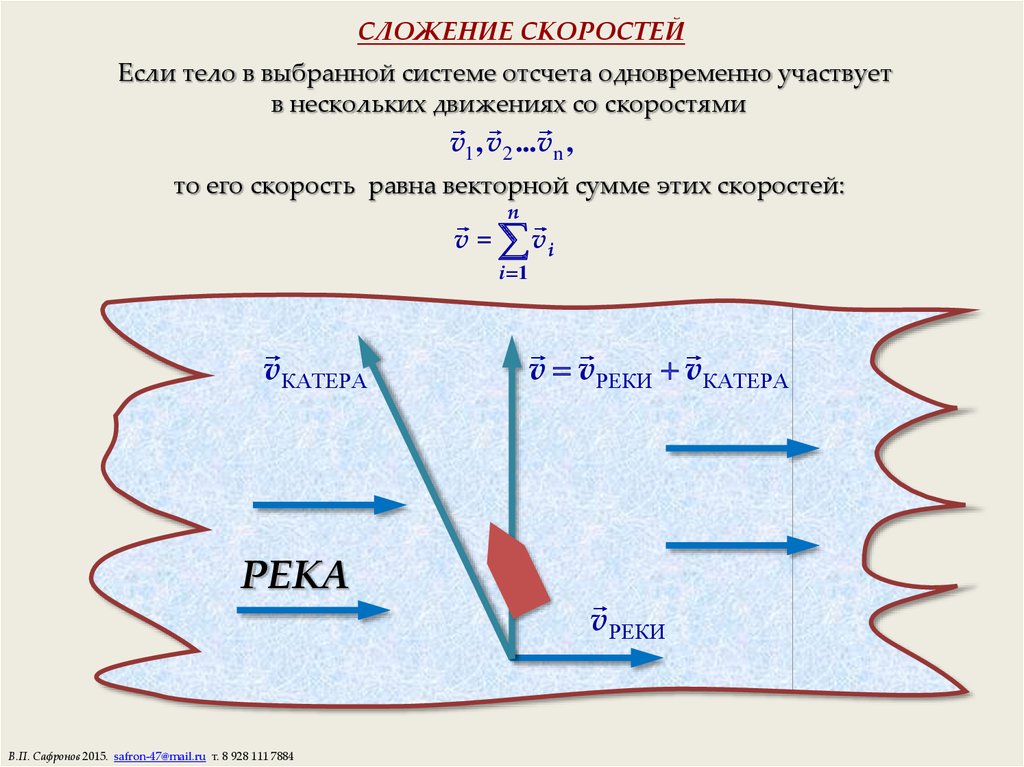
10. СЛОЖЕНИЕ СКОРОСТЕЙ

Если тело в выбранной системе отсчета одновременно участвует
в нескольких движениях со скоростями
v1 , v2 ...vn ,
то его скорость равна векторной сумме этих скоростей:
n
v = vi
i 1
vКАТЕРА
v vРЕКИ vКАТЕРА
РЕКА
vРЕКИ
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

11. УСКОРЕНИЕ

Y
r
a1
r r
a2 a1
a
ay
a , м/с2 — определяет быстроту изменения скорости
(скорость изменения скорости).
v
, м/с 2 .
t
dv
2
Векторное
ускорение
(просто
ускорение)
a
,
м/с
.
0
ax
X
dt
d vy
d vx
Проекции ускорения на оси координат:
ax
, ay
.
dt
dt
dv
.
Тангенциальное ускорение изменяет величину скорости a
dt
Среднее ускорение (схематично) aср
По теореме Пифагора:
a a ax 2 ay 2 .
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

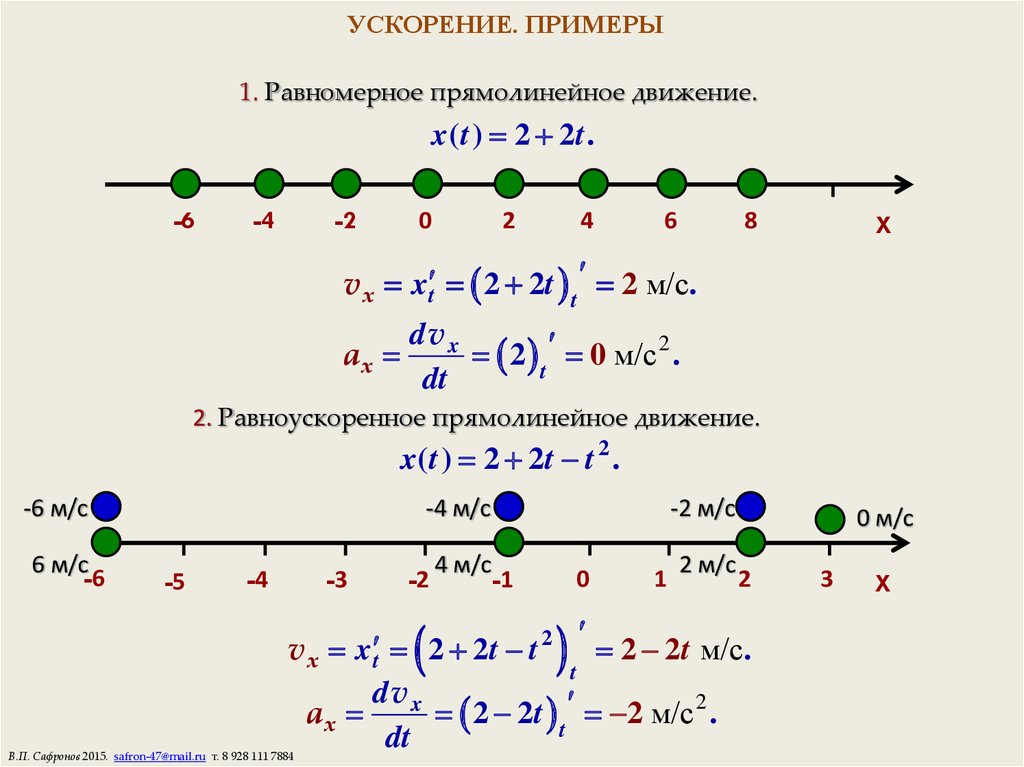
12. УСКОРЕНИЕ. ПРИМЕРЫ

1. Равномерное прямолинейное движение.
x ( t ) 2 2t .
-6
-4
-2
0
2
4
6
8
X
v x x t 2 2t t 2 м/с.
dvx
ax
2 t 0 м/с 2 .
dt
2. Равноускоренное прямолинейное движение.
x ( t ) 2 2t t 2 .
-6 м/с
6 м/с
-6
-4 м/с
-5
-4
-3
-2
4 м/с
-2 м/с
-1
0
1
2 м/с
0 м/с
2
v x x t 2 2t t 2 2 2t м/с.
t
dvx
ax
2 2t t 2 м/с 2 .
dt
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
3
X

13. ТАНГЕНЦИАЛЬНАЯ И НОРМАЛЬНАЯ СОСТАВЛЯЮЩИЕ УСКОРЕНИЯ

В общем случае, ускорение a может быть
a
v
направлено под любым углом к скорости v.
Поэтому его удобно представить как векторную
сумму двух ускорений:
an
a
a a an ; a a a 2 an2 .
a — тангенциальное ускорение — направлено по (против) скорости и определяет
быстроту изменения модуля скорости материальной точки:
dv
a
S .
dt
an — нормальное (центростремительное) ускорение направлено перпендикулярно
скорости и определяет быстроту изменения направления скорости
материальной точки:
an v 2 R ,
где R — радиус кривизны траектории
(радиус окружности, по которой двигалась бы материальная точка при a = 0).
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

14. САМОЛЕТ

a
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

15. 1.1.5. Равномерное прямолинейное движение

r
r r
a 0; v = v0 ; vx 0
r
r r
a 0; v v0 ; vx 0
X
X
ax = 0,
vx (t) = v0x = const, v0 = v0x = const,
x = x0 v0x t ,
x = v0x t ,
x = x0 v0 t ,
x = v0 t
1.1.6. Равноускоренное прямолинейное движение a x const .
r
v0x 0;
ax 0
a x 0;
X
X
a ax , v0 v0 x ;
ax = const ,
vx ( t ) = v0 x ax t ,
x x0 v0 x t ax t / 2,
2
2ax x vx2 v02x .
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
r
v0x 0;
r
v0x 0
vx ( t ) v0 at;
x x0 v0 t a t 2 / 2;
2a x v2 v02 .
ax 0
X

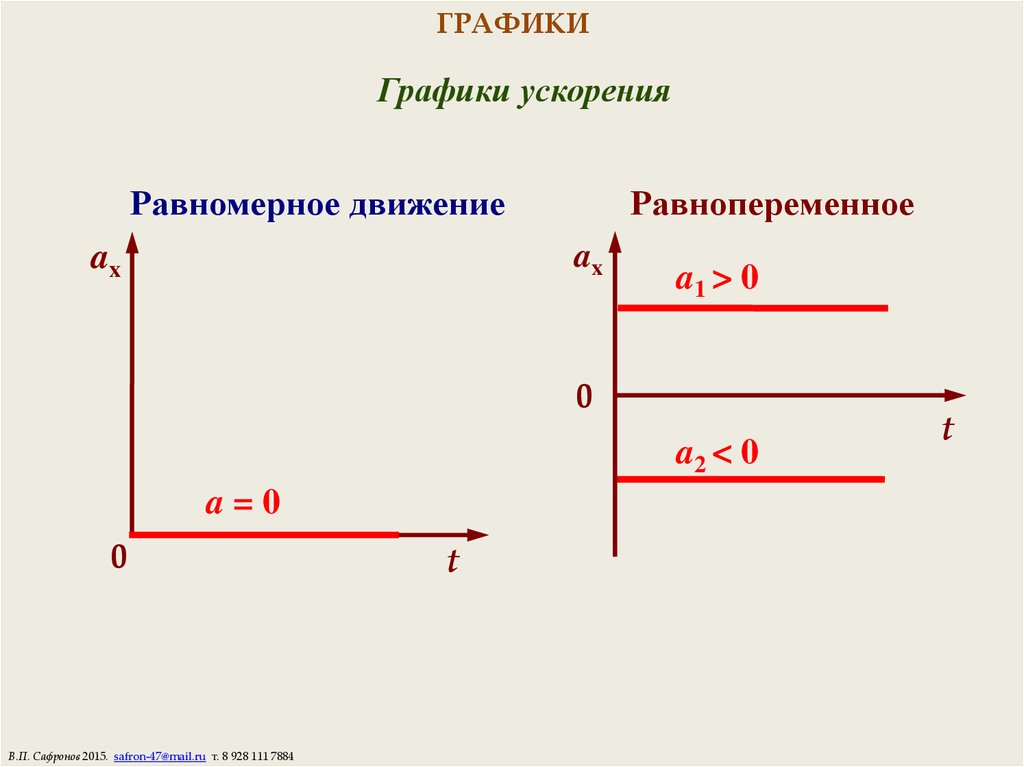
16. ГРАФИКИ

Графики ускорения
Равномерное движение
Равнопеременное
ax
ax
a1 > 0
0
a2 < 0
a=0
0
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
t
t

17. Графики скорости

Равномерное
Равноускоренное
vx
vx
vx > 0
0
vx < 0
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
t
a1 > 0
v0X
0
t
a2 < 0

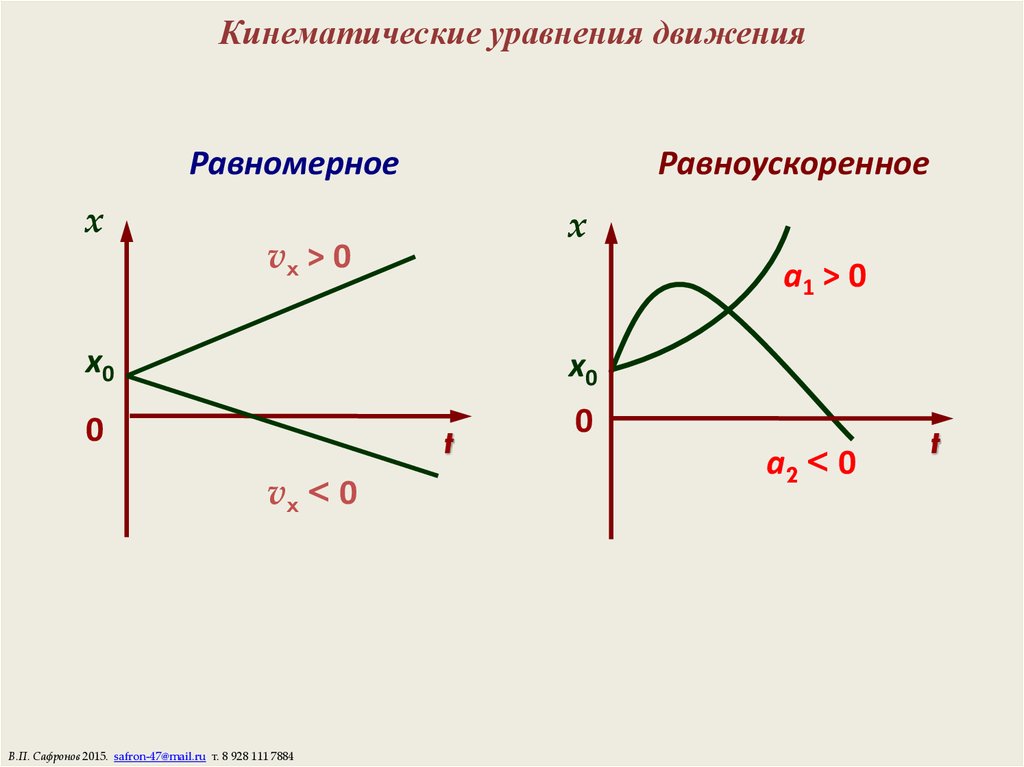
18. Кинематические уравнения движения

Равномерное
x
Равноускоренное
x
vx > 0
a1 > 0
x0
x0
0
0
t
vx < 0
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
a2 < 0
t

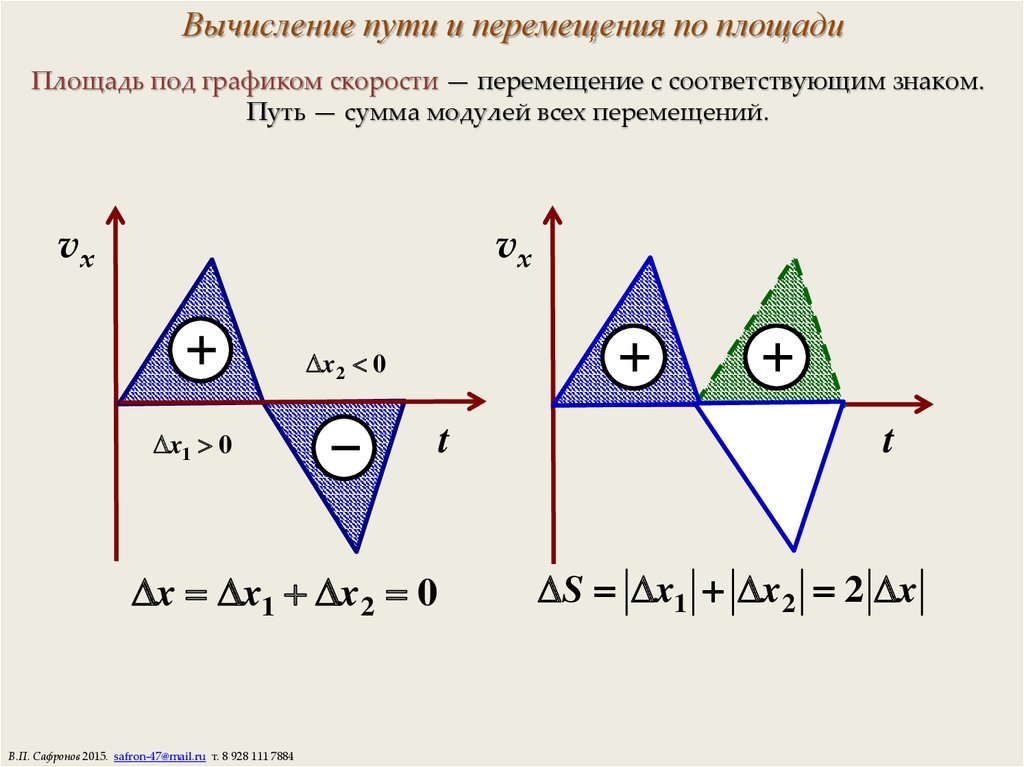
19. Вычисление пути и перемещения по площади

Площадь под графиком скорости — перемещение с соответствующим знаком.
Путь — сумма модулей всех перемещений.
vx
vx
x 2 0
x1 0
x x1 x2 0
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
t
t
S x1 x2 2 x

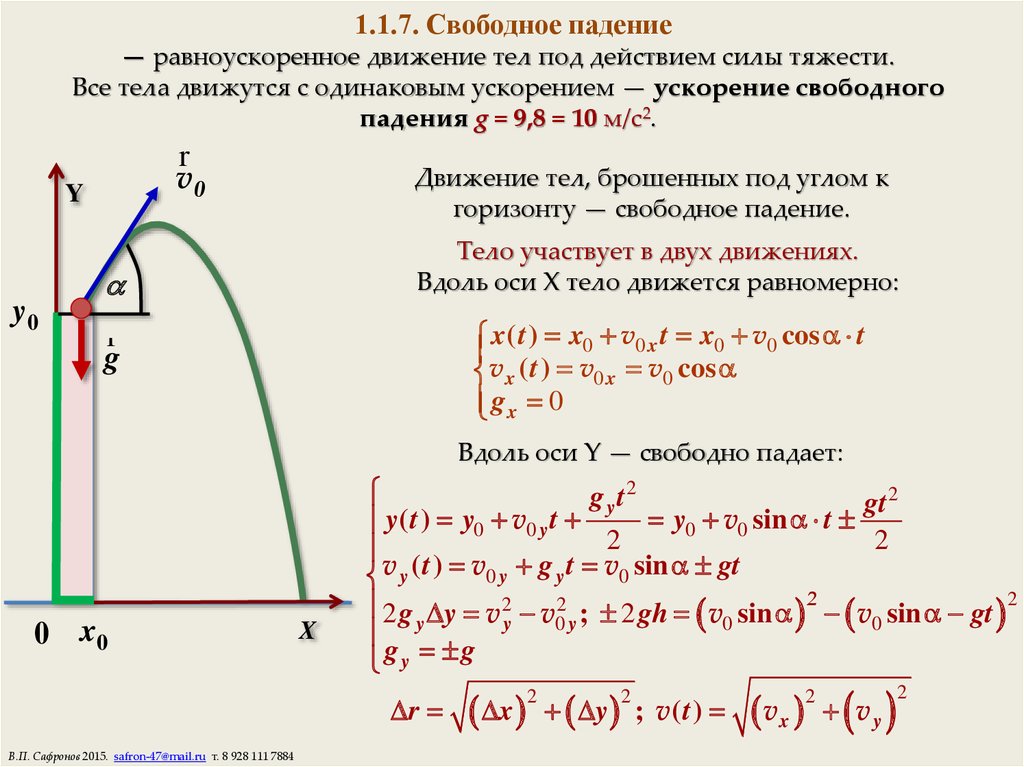
20. 1.1.7. Свободное падение

— равноускоренное движение тел под действием силы тяжести.
Все тела движутся с одинаковым ускорением — ускорение свободного
падения g = 9,8 = 10 м/с2.
r
v0
Y
y0
Движение тел, брошенных под углом к
горизонту — свободное падение.
Тело участвует в двух движениях.
Вдоль оси Х тело движется равномерно:
x ( t ) x0 v0 x t x0 v0 cos t
vx ( t ) v0 x v0 cos
g x 0
r
g
Вдоль оси Y — свободно падает:
0 x0
X
g yt2
gt 2
y0 v0 sin t
y( t ) y0 v0 y t
2
2
v y ( t ) v0 y g y t v0 sin gt
2 g y v2 v2 ; 2 gh v sin 2 v sin gt 2
y
0y
0
0
y
gy g
r
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
x
2
y ; v( t )
2
vx
2
vy
2

21. 1.1.8. Движение точки по окружности

.
r
at
r
aцс
2
a at2 aцс
Движение точки по окружности — происходит за
счет центростремительного ускорения, направленного
перпендикулярно скорости, по радиусу к центру
окружности.
( рад) —угол поворота.
r
v
2 N , где N— число оборотов.
( рад/c) — угловая скорость.
t
T(c) — период — время одного оборота. T = t/N.
S
(c-1, Гц)
φ
— число оборотов за секунду.
N / t 1 / T;
R
2 T 2 .
Связь линейных и угловых переменных:
S ( рад ) R
S R, v R.
Центростремительное ускорение :
aЦС
v2
4 2
2
2 2
R 4 R 2 R.
R
T
Если at = 0, aцс 0, т.е. модуль скорости точки не меняется,
то точка равномерно вращается.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

22. Твердое тело

Твердое тело — не деформируется в процессе движения.
Любое движение твердого тела можно представить в виде
комбинации поступательного и вращательного движений.
Поступательное движение — тело можно считать материальной точкой
( рад)
При вращательном движении все точки движутся по
концентрическим окружностям, центры которых
лежат на одной прямой, называемой осью вращения.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

23. КОНЕЦ КИНЕМАТИКИ

В.П. Сафронов 2015. [email protected] т. 8 928 111 7884