Законы сохранения в механике

1. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

ЕГЭ. ФИЗИКА
РЕПЕТИЦИЯ ПО ФИЗИКЕ
Владимир Петрович Сафронов 2015
г. Ростов-на-Дону
звоните т. 8 928 111 7884
пишите [email protected]
ЗАКОНЫ СОХРАНЕНИЯ
В МЕХАНИКЕ

2. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

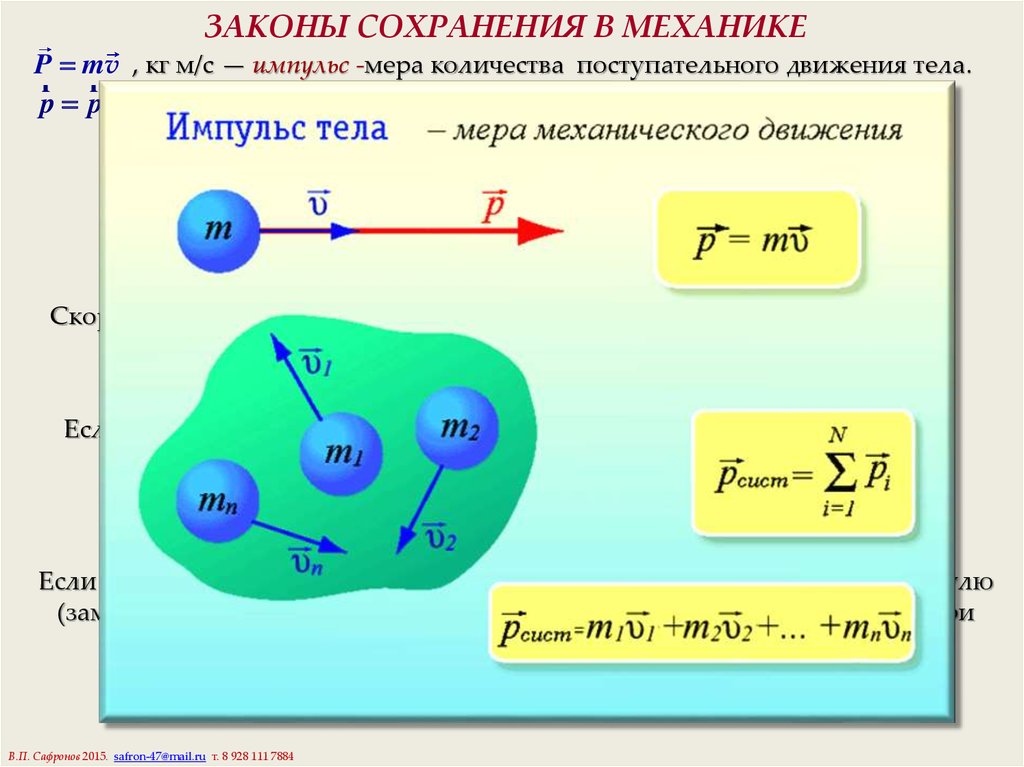
P mv , кг м/с — импульс -мера количества поступательного движения тела.
r r r
p p1 p2 ... импульс системы тел.
Импульс зависит от выбора системы отсчета
Второй закон Ньютона (основной закон динамики).
v v МЯГКОЕ
mv - ТВЕРДОЕ
mv
( mv)
P
F ma m
2
t
1
2
t
1
t
F
t
.
Скорость изменения импульса тела в инерциальной системе отсчета равна
силе, приложенной к телу.
Следствие.
Если равнодействующая сила равна нулю, то импульс тела не меняется:
P
0
t
P const .
Закон сохранения импульса.
Если результирующая внешняя сила, действующая на систему тел, равна нулю
(замкнутая система), то импульс системы тел не меняется (сохраняется) при
любых событиях внутри системы
r
r
r
r
m1v1 m2v2 ... m1 v1 m2 v2 ...
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

3. Примеры

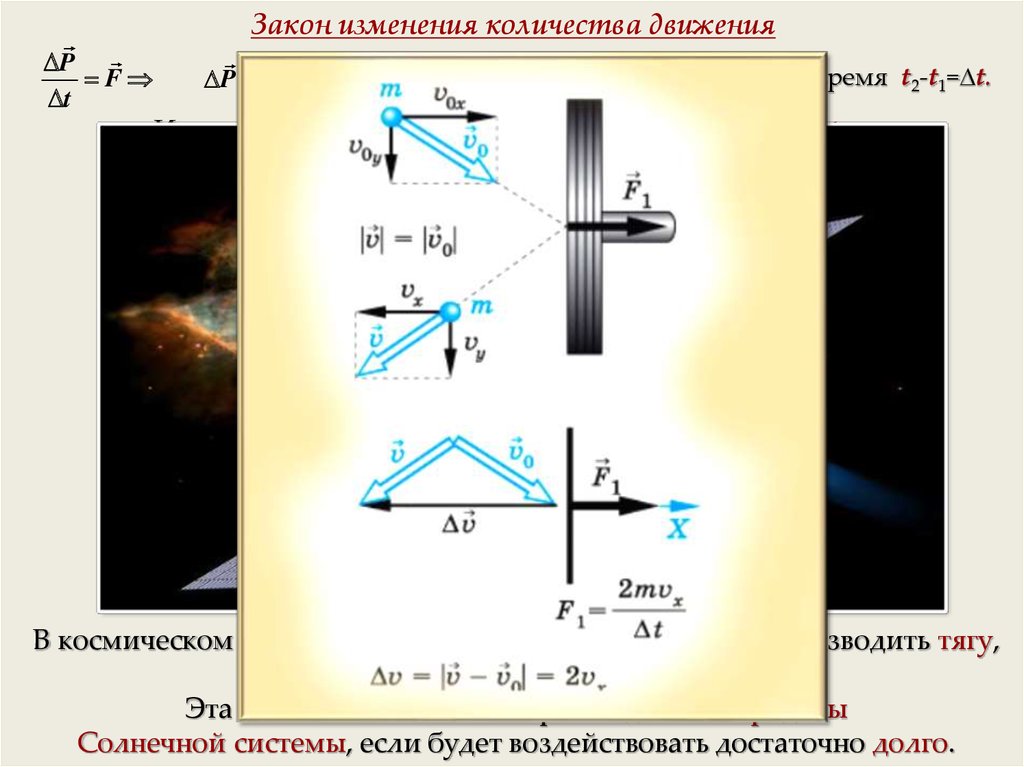
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

4. Закон изменения количества движения

P
F
t
P F t
P2 P1 F t 2 t1 — импульс силы за время t2-t1= t.
Изменение импульса (количества движения) за время t
равно импульсу силы за это же время.
В космическом пространстве ионный двигатель будет производить тягу,
эквивалентную весу почтовой открытки.
Эта тяга может вывести корабль даже за пределы
Солнечной системы, если будет воздействовать достаточно долго.

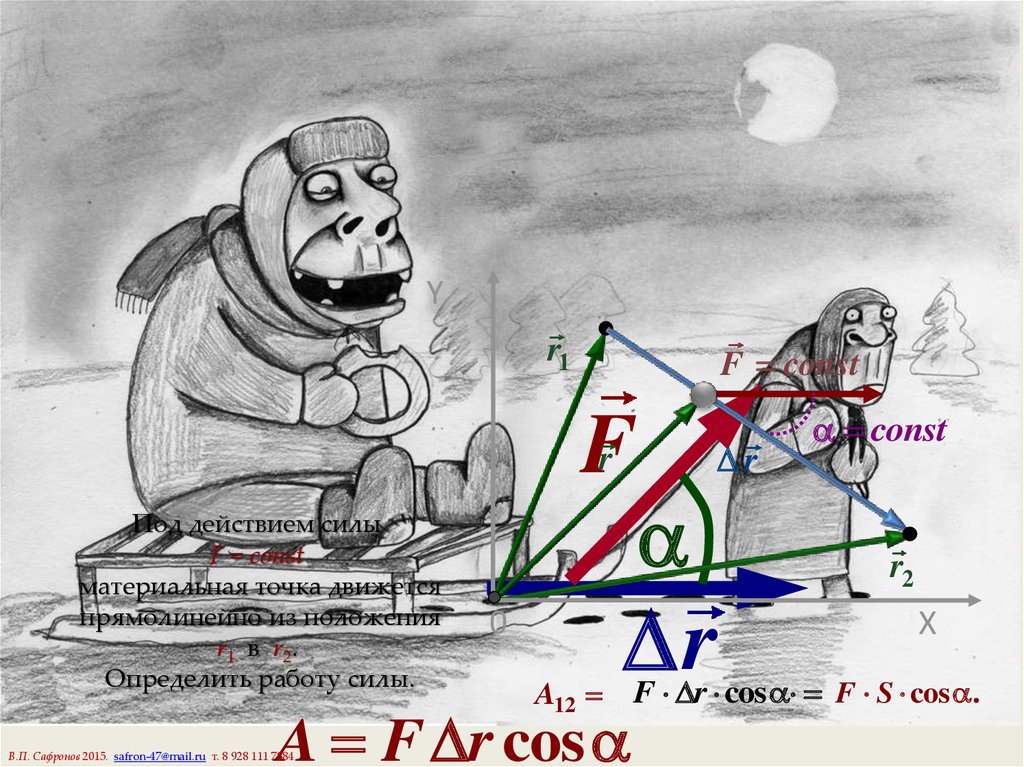
5. РАБОТА

A , Дж = Н∙м, постоянной силы F при перемещении r определяется формулой
r
F
A F r cos Fx x,
где — угол между силой и перемещением.
Fx
0 90 , A 0;
90, A 0;
90 180 , A 0.
x Работа численно равна площади под графиком Fx(x)
r
r x
Y
Fx
r1
A
x
Под действием силы
F = const
материальная точка движется
прямолинейно из положения
r1 в r2.
Определить работу силы.
0
F const
Fr r
r
r2
X
A12 F r cos F S cos .
A F r cos
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
const

6. Мощность силы

Мощность N, Дж/с=Вт
это скорость совершения работы или скорость изменения энергии.
N
dA dE
.
dt
dt
Мощность силы
A F r cos
F v cos .
N
t
t
N F v cos
Мощность силы равна скалярному произведению силы
на скорость точки ее приложения.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

7. Энергия

это общая количественная мера движения и взаимодействия
всех видов материи.
Понятие энергии объединяет все явления в природе.
Энергия не возникает из ничего и не исчезает в никуда,
а только переходит из одной формы в другую.
При этом может совершаться механическая работа.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

8. Кинетическая энергия

Энергия E,W,U; Дж. Механическая энергия определяет работоспособность
(запас работы) тела.
K, Дж — это запас работы, связанный с движением тела.
Кинетическая энергия, как и скорость, величина относительная.
Ее значение можно изменить выбором системы отсчета.
Для материальной точки:
mv 2
p2
Ek K
.
2
2m
Для системы материальных точек:
mi vi 2 N pi 2
Ek K
,
2
i
i 2 mi
N
mi , vi , pi — масса, скорость и импульс i-ой частицы, N — число частиц.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

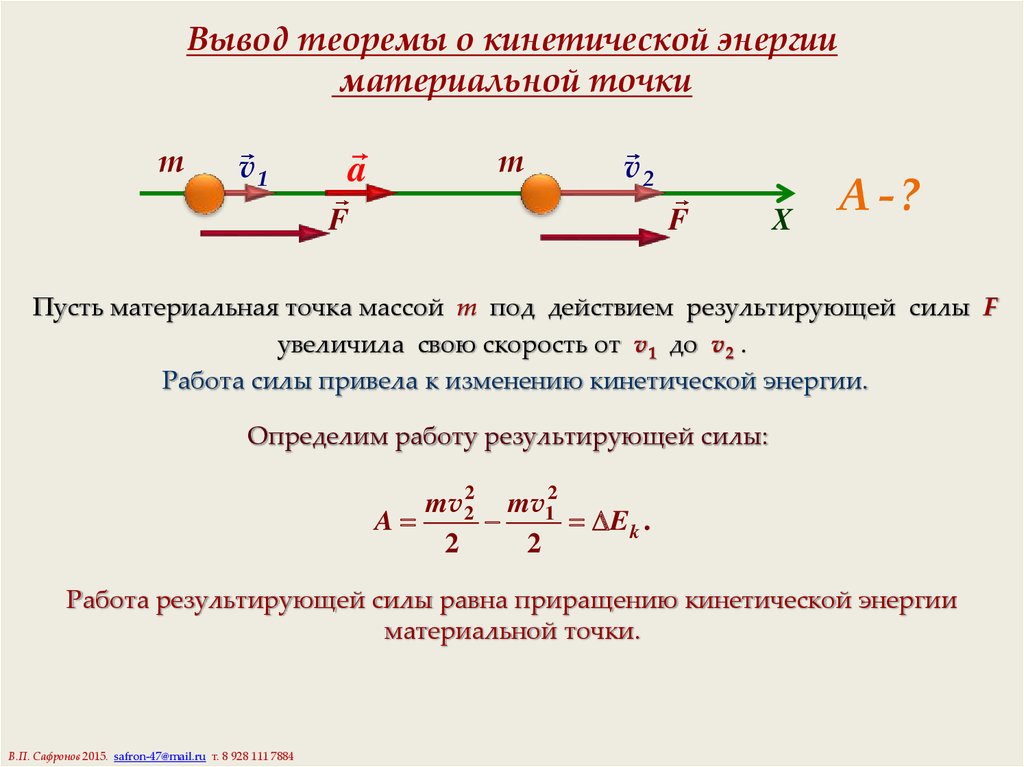
9. Вывод теоремы о кинетической энергии материальной точки

m
v1
a
m
v2
F
F
X
A -?
Пусть материальная точка массой m под действием результирующей силы F
увеличила свою скорость от v1 до v2 .
Работа силы привела к изменению кинетической энергии.
Определим работу результирующей силы:
mv22 mv12
A
E k .
2
2
Работа результирующей силы равна приращению кинетической энергии
материальной точки.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

10. Поле консервативных (потенциальных) сил.

Консервативными (потенциальными) являются гравитационное поле и
создаваемая им сила тяжести, электростатические силы и поля, поле
упругих сил.
При движении материальной точки в поле консервативных сил работа
не зависит от траектории, а определяется только начальным и конечным
положением точки.
Силы, не обладающие этими свойствами, называются диссипативными
(например, силы трения).
Работа этих сил переводит энергию из механической в другие формы,
например, во внутреннюю энергию.
Потенциальная энергия — запас работы, связанный с взаимодействием и
расположением тел
Потенциальная энергия материальной точки в поле потенциальных сил
U ( r ), Eп , Дж — это запас работы, которую могут совершить консервативные
силы при перемещении тела из данной точки r1 в точку r2 ,
принятую за начало отсчета потенциальной энергии.
Потенциальная энергия — величина относительная,
зависящая от выбора начала отсчета энергии.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

11. Потенциалная энегия тела, поднятого на высоту h

потенциальная энергия тела массой m, находящегося
на высоте h над поверхностью земли, равна
работе силы тяжести mg при перемещении тела
из точки r1 в любую точку r2,
лежащую на поверхности земли,
принятой за начало отсчета энергии:
r1
mg
h
r2
r2
r2
r1
r1
U ( r1 ) A mgdr mg dr mg r2 r1 mgh
U ( r1 ) U ( h) mgh.
Следствие 1.
Работа, совершаемая силами поля при переходе
материальной точки из положения r1 в r2,
равна разности потенциальных энергий в этих точках:
A12 U1 U 2 mgh1 mgh2
Следствие 2.
Работа консервативных сил при перемещении материальной точки
осуществляется за счет убыли ее потенциальной энергии:
A U .
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

12. Потенциальная энергия деформированной пружины.

По закону Гука сила упругости
Fупр k x,
k — жесткость пружины,
x — удлинение.
При изменении длины пружины от 0 до x совершается работа и
запасается потенциальная энергия
kx 2
kx
F
F
x 21
Eп А U x Fупр x12
ср
2
2
kx 2
U x
.
2
Потенциальная энергия поля центральных сил
Центральными называются силы, линия действия которых всегда
проходит через одну и ту же точку.
Например, для гравитационных сил эта точка — центр масс.
Fгравит G
Mm
r2
M , m — массы, взаимодействующих тел,
r — расстояние между центрами масс.
E П ( r ) G
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
Mm
, EП ( r ) 0.
r

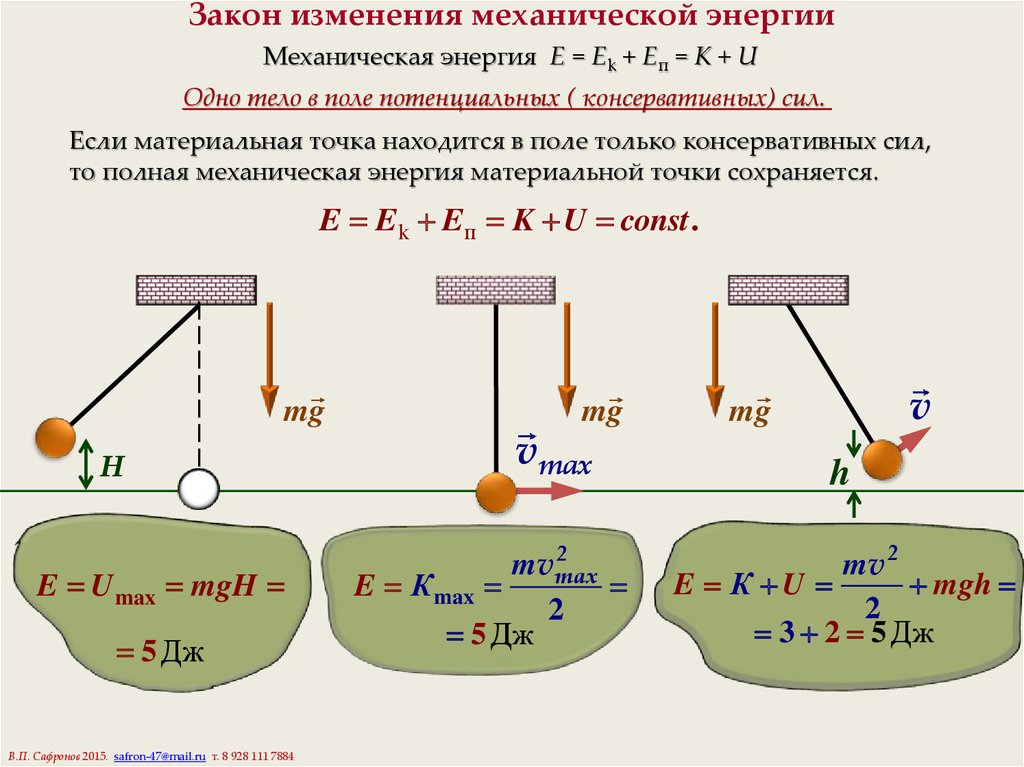
13. Закон изменения механической энергии

Механическая энергия E = Ek + Eп = K + U
Одно тело в поле потенциальных ( консервативных) сил.
Если материальная точка находится в поле только консервативных сил,
то полная механическая энергия материальной точки сохраняется.
E Ek Eп K U const .
mg
H
E U max mgH
5 Дж
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
mg
vmax
2
mv max
E К max
2
5 Дж
v
mg
h
mv 2
E К U
m gh
2
3 2 5 Дж

14. Закон изменения механической энергии

Работа непотенциальных сил (сила тяги, сила трения) приводит к
изменению механической энергии
E А НЕПОТЕНЦИАЛЬНЫЕ СИЛЫ
А НЕПОТЕНЦИАЛЬНЫЕ СИЛЫ AТР , AТЯГИ .
Закон сохранения механической энергии
Если непотенциальные силы отсутствуют или Анепот силы = 0, то механическая
энергия системы не меняется (сохраняется):
E 0
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
EI состояние EII состояние .

15. 3.5. Соударения

Соударением (ударом) называются кратковременные взаимодействия тел,
при которых возникающие силы столь велики,
что внешними силами можно пренебречь
и рассматривать соударяющиеся тела как замкнутую систему.
Абсолютно неупругий удар
При таком ударе тела объединяются и движутся как единое целое.
Взрыв — неупругий удар наоборот (время течет в прошлое).
При неупругом ударе не выполняется
закон сохранения механической энергии, так как
часть или вся кинетическая энергия переходит
во внутреннюю энергию, тратится на работу по деформации.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

16. Неупругий удар

При неупругом ударе выполняется
закон сохранения импульса:
p1
p2
p p1 p2 .
Или в проекциях на координатные оси:
p p1 p2
x ) mvX m1v1X m2v2X
y) mvY m1v1Y m2v2Y
m m1 m 2 .
p2
p1
Зная массы и скорости исходных частиц, можно определить
p2
.
скорость и импульс объединенного тела после удара E k
2( m1 m2 )
и его кинетическую энергию.
Изменение кинетической энергии системы
после неупругого удара
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
p12
p22
p2
E
.
2( m1 m2 ) 2m1 2m2

17. Абсолютно упругий удар

После такого удара тела полностью восстанавливают свою форму и объем.
При упругом ударе выполняются закон сохранения импульса и
закон сохранения механической энергии.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

18. Рассмотрим соударение двух упругих шаров массами m и M.

До соударения большой шар покоится, малый движется со скоростью u
и импульсом p = mu.
MV
p mu
M
p
Для описания удара используются
закон сохранения импульса
x
mu mv MV
и закон сохранения энергии
mu 2 mv 2 MV 2 .
mv
Рассмотрим центральный удар, при котором линия удара проходит
через центр инерции обоих тел.
p mu
M mv
MV
Тогда в проекциях на ось x:
1) m ux vx MVx
x
Разделив второе уравнение на первое,
имеем
V x ux v x .
2) m ux2 v x2 M Vx2
Подставляя в первое уравнение, получаем скорость налетавшего шара
после удара:
vx
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884
m M
ux .
m M

19. Упругий удар

Если массы шаров равны m = M, налетающий шар останавливается, v m M u .
x
x
m M
а второй движется с его скоростью.
Если шар ударяется о стенку
M ,
vx ux ,
то, шар отскакивает с начальной скоростью u,
причем стенке передается импульс
2mu.
В.П. Сафронов 2015. [email protected] т. 8 928 111 7884

20. конец

В.П. Сафронов 2015. [email protected] т. 8 928 111 7884