Similar presentations:
Механические колебания
1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
ЕГЭ. ФИЗИКАРЕПЕТИЦИЯ ПО ФИЗИКЕ
Владимир Петрович Сафронов 2015
г. Ростов-на-Дону
Звоните: т. 8 928 111 7884
Пишите: safron-47@mail.ru
2. Основные понятия
Колебаниями называются процессы в той или иной степениповторяющиеся во времени.
t
Период колебаний T, с — время одного полного колебания T .
N
N
Частота , Гц — количество полных колебаний, совершаемых
.
за единицу времени.
t
Циклическая ( круговая) частота , рад/с
0
1
2
2
. .
t
T
T
Гармонические колебания — это процессы, в
Гармонические колебания.
x
Начальная фаза 0 = 0
x t x0 sin t 0 .
x0
0
которых физические величины меняются по
гармоническому закону (рис):
2
T /2
T
x0
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
-фаза
x0 — амплитуда колебаний — максимальное
значение колеблющейся величины. Например,
наибольшее отклонение маятника x0,
t- время
наибольшая скорость v0 и ускорение
маятника a0.
0
t 0 .
Фаза колебаний
t
Начальная фаза колебаний 0 .
3. Скорость и ускорение гармонических колебаний
Кинематическое уравнение движенияx t x0 sin t 0
Скорость колебаний, по определению,
является первой производной смещения по времени: v t x t v0 cos t 0
v0 x0 — амплитуда скорости.
Ускорение определяется второй производной:
a t x t 2 a0 sin t 0
a0 x0 2 — амплитуда ускорения.
a t 2 x t .
Динамическое описание.
Если II закон Ньютона имеет вид max t kx t ,
то, движение является гармоническим колебанием x ( t ) x0 sin( 0 t 0 )
с циклической частотой
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
k
m
и периодом T 2
.
m
k
4. КОЛЕБАНИЯ МАЯТНИКОВ
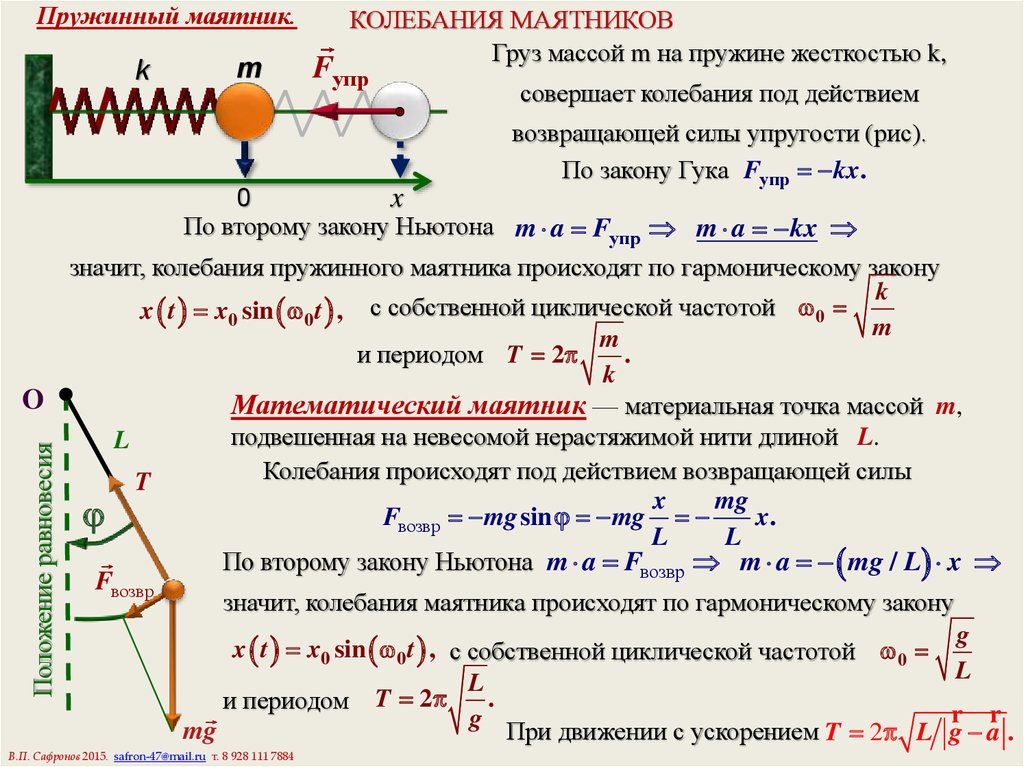
Пружинный маятник.k
m
КОЛЕБАНИЯ МАЯТНИКОВ
Груз массой m на пружине жесткостью k,
Fупр
совершает колебания под действием
возвращающей силы упругости (рис).
По закону Гука Fупр kx .
Положение равновесия
0
x
По второму закону Ньютона m a Fупр m a kx
значит, колебания пружинного маятника происходят по гармоническому закону
k
с
собственной
циклической
частотой
x t x0 sin 0 t ,
0
m
m
и периодом T 2
.
k
O
Математический маятник — материальная точка массой m,
подвешенная на невесомой нерастяжимой нити длиной L.
L
Колебания происходят под действием возвращающей силы
T
x
mg
Fвозвр mg sin mg
x.
L
L
По второму закону Ньютона m a Fвозвр m a mg / L x
Fвозвр
значит, колебания маятника происходят по гармоническому закону
g
x t x0 sin 0 t , с собственной циклической частотой 0
L
L
.
и периодом T 2
r r
g
mg
При движении с ускорением T 2 L g a .
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
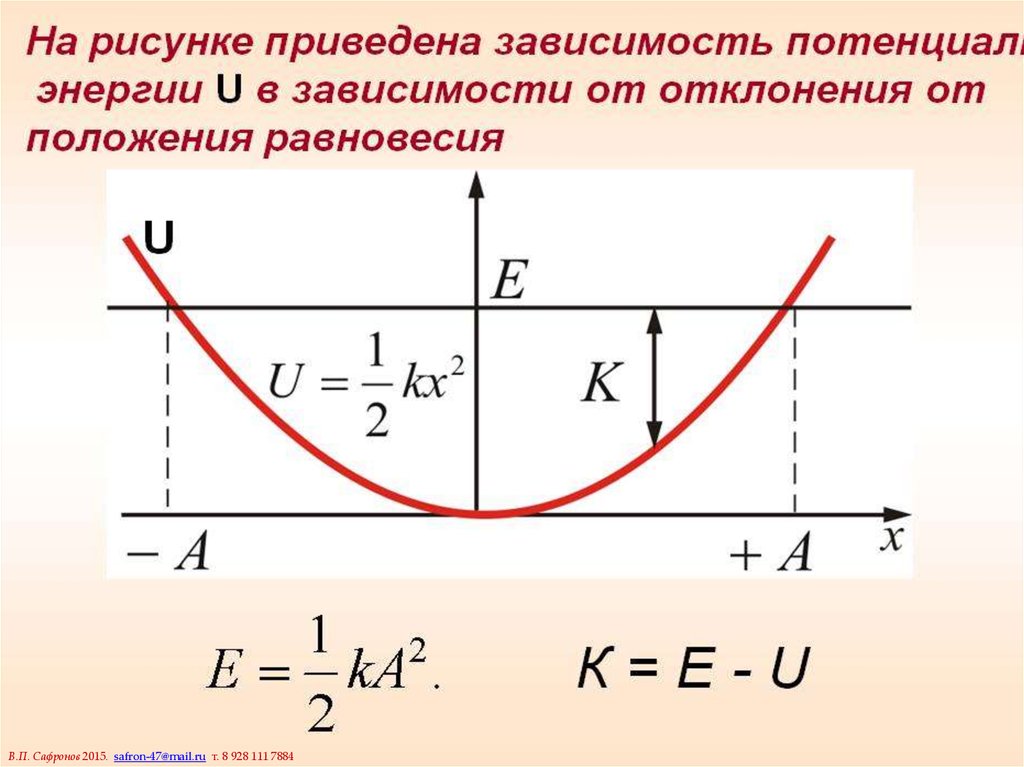
5. Превращение энергии при гармонических колебаниях
При свободных гармонических колебаниях выполнятся закон сохранениямеханической энергии: в любой точке траектории сумма кинетической и
потенциальной энергий не меняется.
Например, для пружинного маятника:
kx 2 kx02
U
sin 2 t — потенциальная энергия в момент времени t.
2
2
m 2 x02
mv 2 mv02
2
K
cos t
cos2 t — кинетическая энергия в момент времени t.
2
2
2
k x02 mv02
mv 2 kx 2 kx02 2
2
E K U
sin t cos t
const
2
2
2
2
2
Для математического маятника:
mv02
mv 2
E K U
mgh mgH
const
2
2
x0 , x — амплитуда и текущее значение смещения,
H, h — максимальная и текущая высота подъема материальной точки,
v0 , v — максимальная и текущая скорость материальной точки.
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
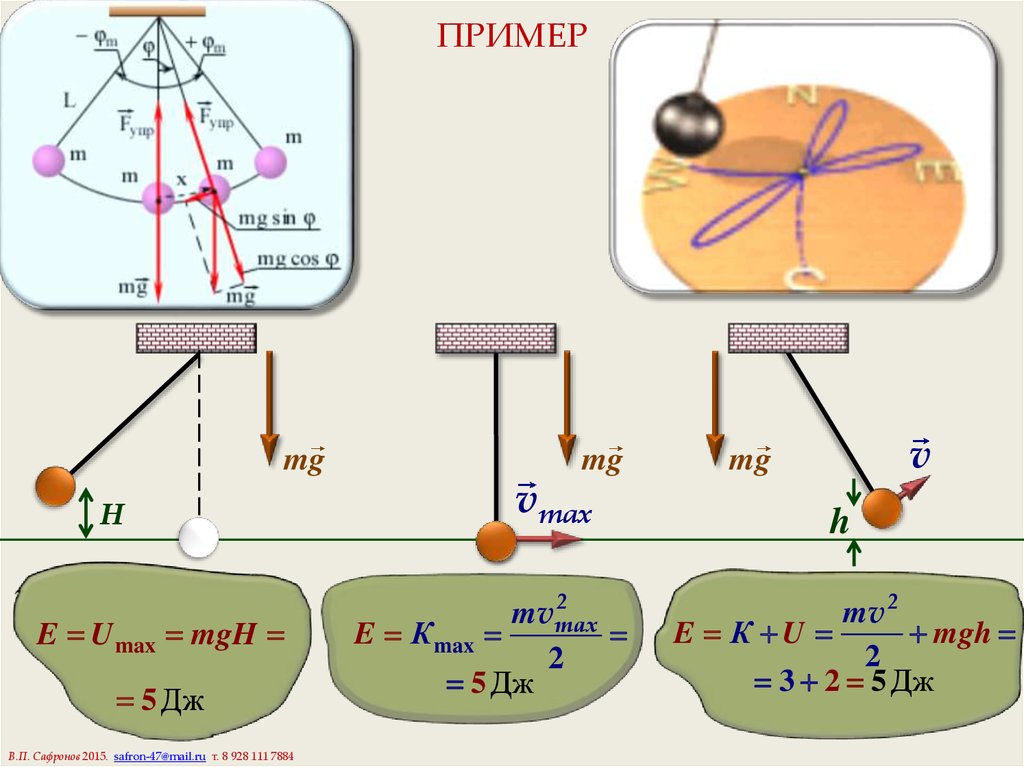
6. ПРИМЕР
mgH
E U max mgH
5 Дж
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
mg
vmax
2
mv max
E К max
2
5 Дж
v
mg
h
mv 2
E К U
m gh
2
3 2 5 Дж
7. Пружинный маятник
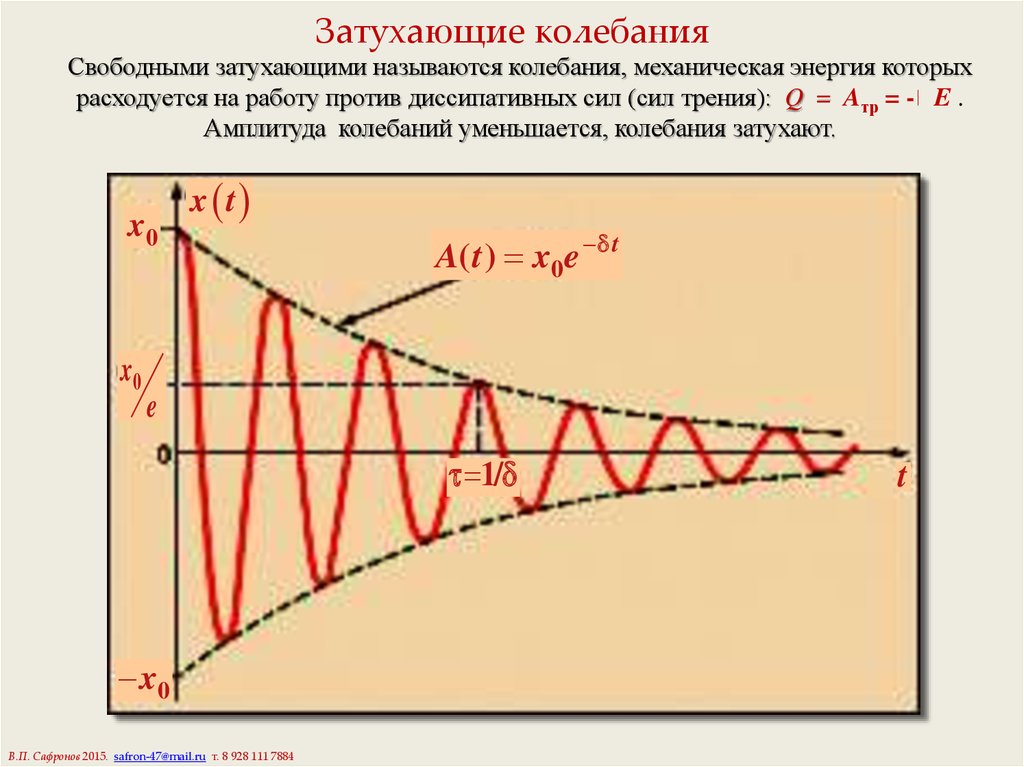
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 78848. Затухающие колебания
Свободными затухающими называются колебания, механическая энергия которыхрасходуется на работу против диссипативных сил (сил трения): Q = Aтр = - E .
Амплитуда колебаний уменьшается, колебания затухают.
x0
x0
x t
A( t ) x0e t
e
1/
x0
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
t
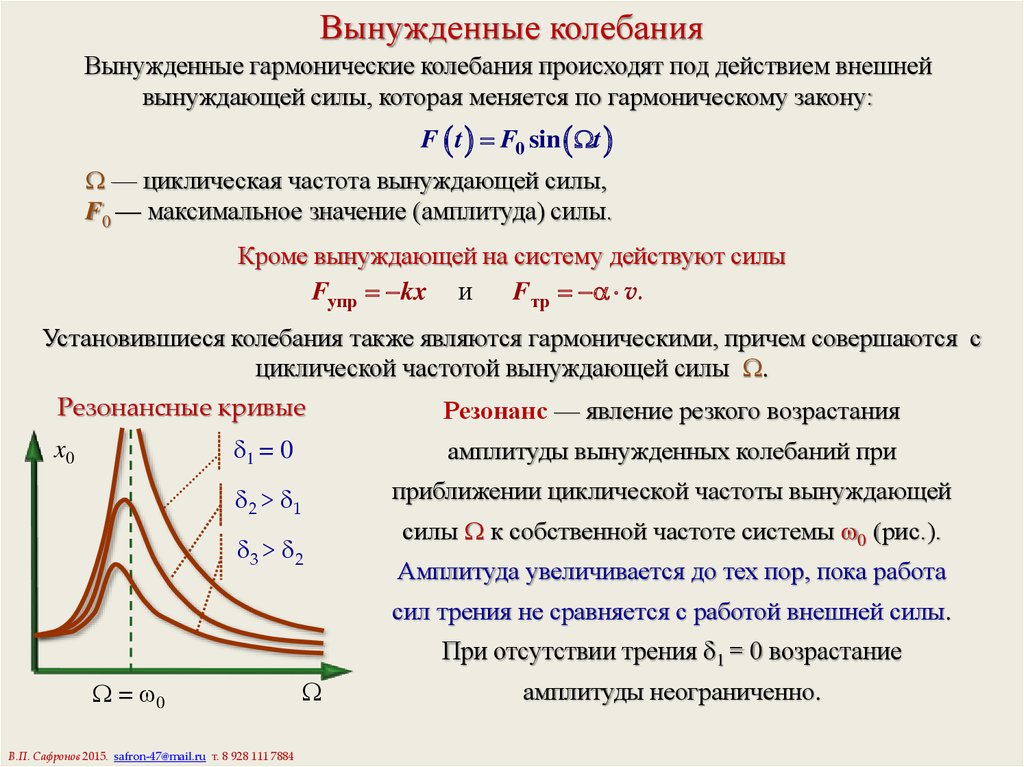
9. Вынужденные колебания
Вынужденные гармонические колебания происходят под действием внешнейвынуждающей силы, которая меняется по гармоническому закону:
F t F0 sin t
— циклическая частота вынуждающей силы,
F0 — максимальное значение (амплитуда) силы.
Кроме вынуждающей на систему действуют силы
Fупр kx и
Fтр v.
Установившиеся колебания также являются гармоническими, причем совершаются с
циклической частотой вынуждающей силы .
Резонансные кривые
x0
Резонанс — явление резкого возрастания
1 = 0
амплитуды вынужденных колебаний при
2 > 1
приближении циклической частоты вынуждающей
3 > 2
силы к собственной частоте системы 0 (рис.).
Амплитуда увеличивается до тех пор, пока работа
сил трения не сравняется с работой внешней силы.
При отсутствии трения 1 = 0 возрастание
= 0
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
амплитуды неограниченно.
10. УПРУГИЕ ВОЛНЫ
•Распространение колебаний в упругих средах происходит за счет упругих волн.Упруго деформированный участок среды, возвращая начальную форму, деформирует
соседние участки и т.д. Волны переносят энергию и импульс без переноса вещества.
Поперечной называется волна, в которой частицы
среды колеблются в направлении, перпендикулярном
направлению распространения волны (наблюдаются
v
только в твердых телах, рис. а).
а)
Продольной называется волна, в которой колебание частиц
происходит в направлении распространения волны, изменяя
v
б)
y
плотность среды (наблюдаются в газах, жидкостях и
твердых телах, рис. б).
Длина волны , м — расстояние между двумя ближайшими
точками среды, которые колеблются в одинаковой фазе.
Волновой поверхностью (фронт волны) называется
x
геометрическое место точек среды, которые колеблются
в одной фазе. По форме фронта волны делятся на плоские,
цилиндрические, сферические.
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
11. Волны
12. Связь длины волны со скоростью ее распространения v
Связь длины волны со скоростью ее распространения vДлина волны равна расстоянию, которое проходит волна за время, равное
периоду колебаний источника волн:
c T;
c
Звуковые волны — упругие волны в слышимом диапазоне частот:
инфразвук, 16 Гц < слышимый диапазон < 20 000 Гц, ультразвук.
Скорость звука
vвоздух = 330 м/с; vвода = 1 500 м/с; vсталь = 5 000 м/с.
Громкость (сила) звука определяется квадратом амплитуды колебаний
частицы среды.
Высота тона определяется частотой звуковых колебаний: чем больше
частота, тем выше тон.
Дифракция — огибание волнами препятствий.
Интерференция — сложение двух или более когерентных (одинаковых по частоте)
волн, в результате которого возникают устойчивые области усиления (max)
и ослабления (min) колебаний.
В.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884
13. конец
КОНЕЦВ.П. Сафронов 2015. safron-47@mail.ru т. 8 928 111 7884







 physics
physics








