Механические колебания. 11 класс

1. Механические колебания

2.

Механические колебания –
это движения, которые
точно или приблизительно
повторяются через
определенные интервалы
времени

3.

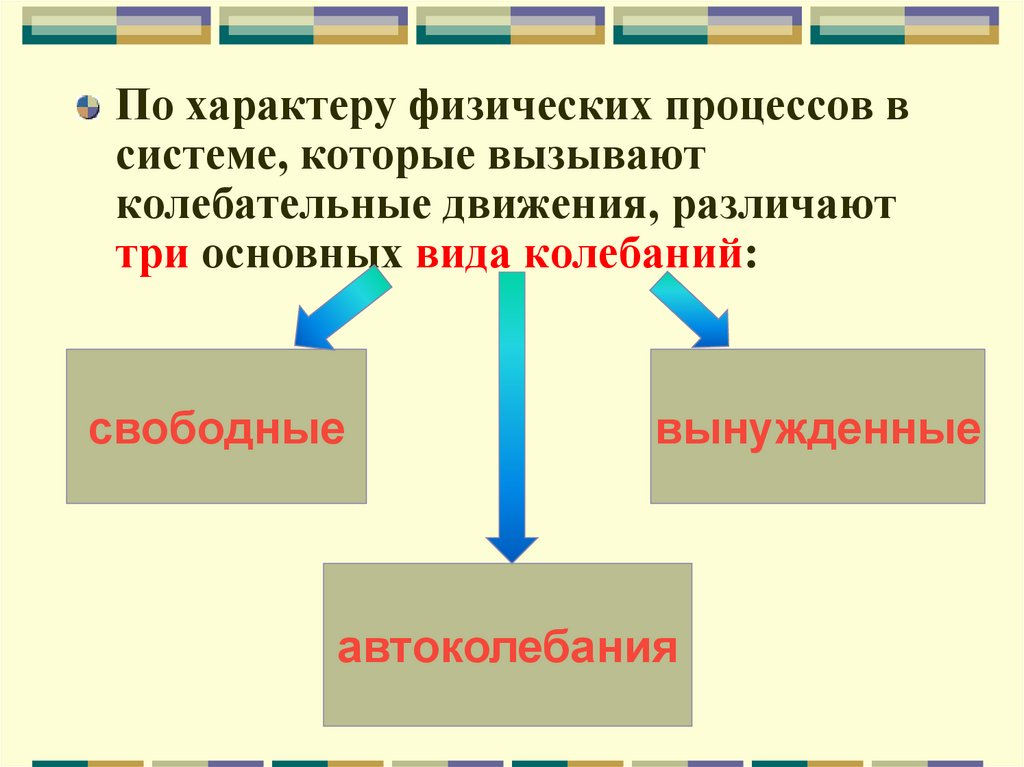
По характеру физических процессов в
системе, которые вызывают
колебательные движения, различают
три основных вида колебаний:
свободные
вынужденные
автоколебания

4.

Вынужденные колебания – это
колебания, которые происходят под
действием внешней, периодически
изменяющейся силы (пример: качели).

5.

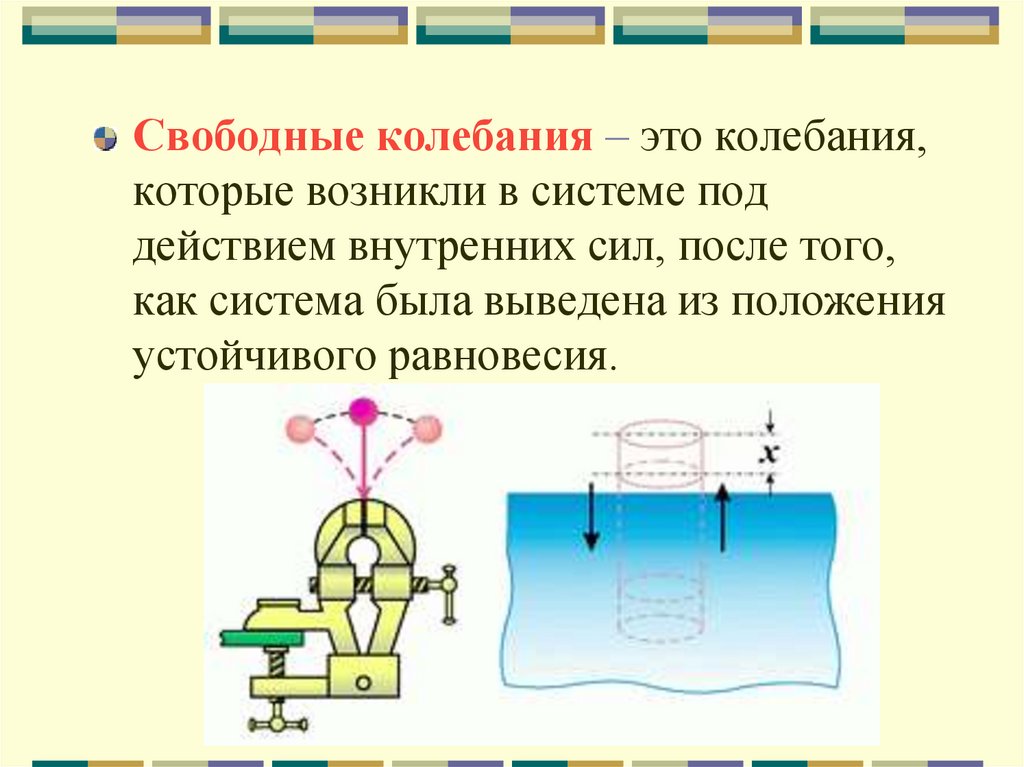
Свободные колебания – это колебания,
которые возникли в системе под
действием внутренних сил, после того,
как система была выведена из положения
устойчивого равновесия.

6.

Автоколебаниями
называются
незатухающие
колебания, которые
Часы с балансиром.
могут существовать
Спусковой механизм
в системе без
часов:
воздействия на неё
1 — балансир;
2 — анкерная вилка;
внешних
3 — спусковое колесо
периодических сил.
Маятниковые часы

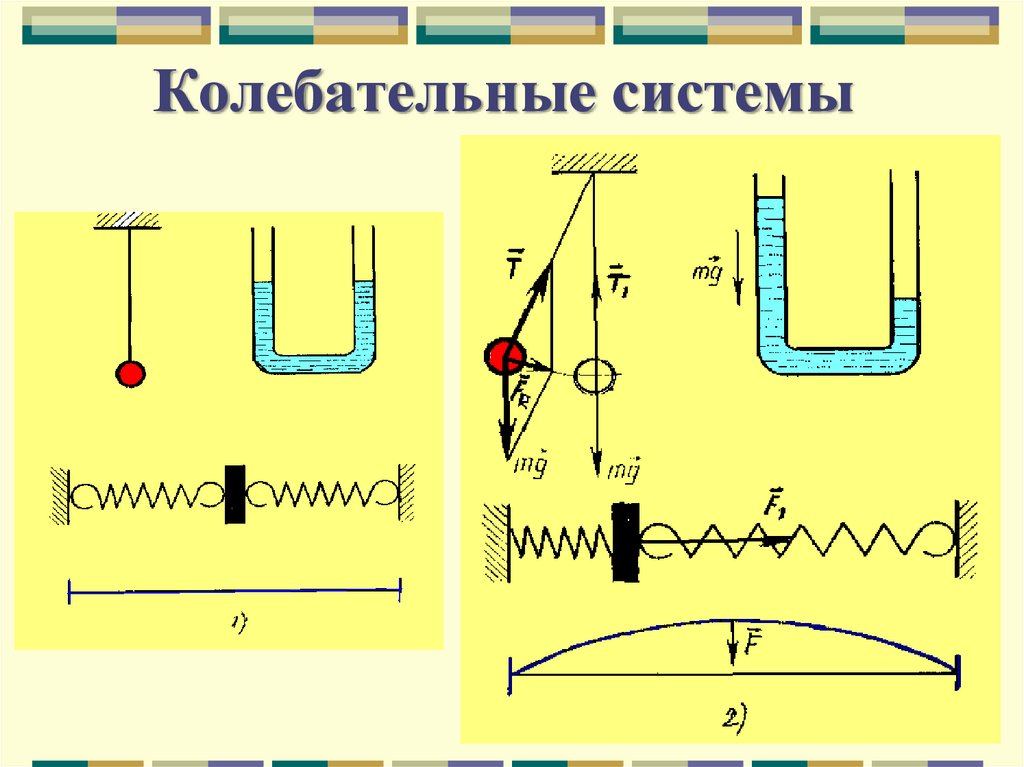
7. Колебательные системы

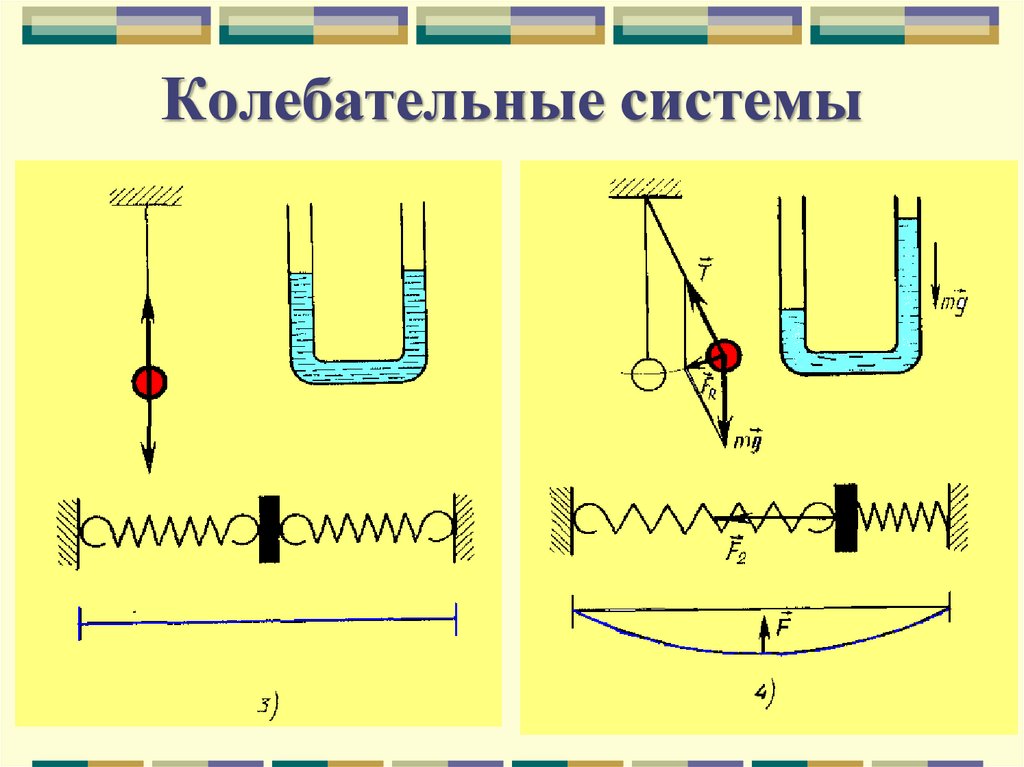
8. Колебательные системы

9. Условия возникновения колебаний

Наличие положения устойчивого равновесия, при
котором равнодействующая сила равна нулю.
Хотя бы одна сила должна зависеть от координат.
Наличие в колеблющейся материальной точке
избыточной энергии.
Если вывести тело из положения равновесия, то
равнодействующая не равна нулю.
Силы трения в системе малы.
Для возникновения колебаний тело необходимо вывести
из положения равновесия, сообщив либо кинетическую
энергию (удар, толчок), либо – потенциальную (отклонение
тела от положения равновесия).

10. Превращение энергии при колебательном движении

11. Превращение энергии при колебательном движении

За одно полное колебание
2
mV
mV
mgh
mgh
2
2
1
max
max
1
2
const
Если нет сил трения и сопротивления, то
выполняется закон сохранения механической
энергии: Екин. + Епот. = const

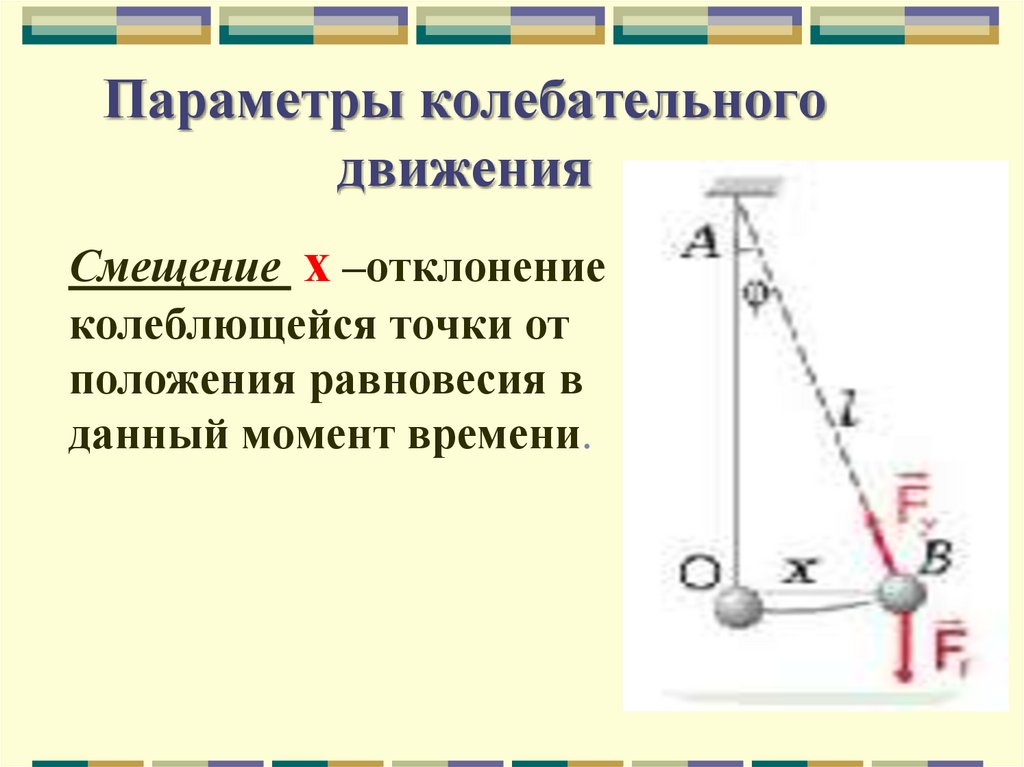
12. Параметры колебательного движения

Смещение х –отклонение
колеблющейся точки от
положения равновесия в
данный момент времени.

13.

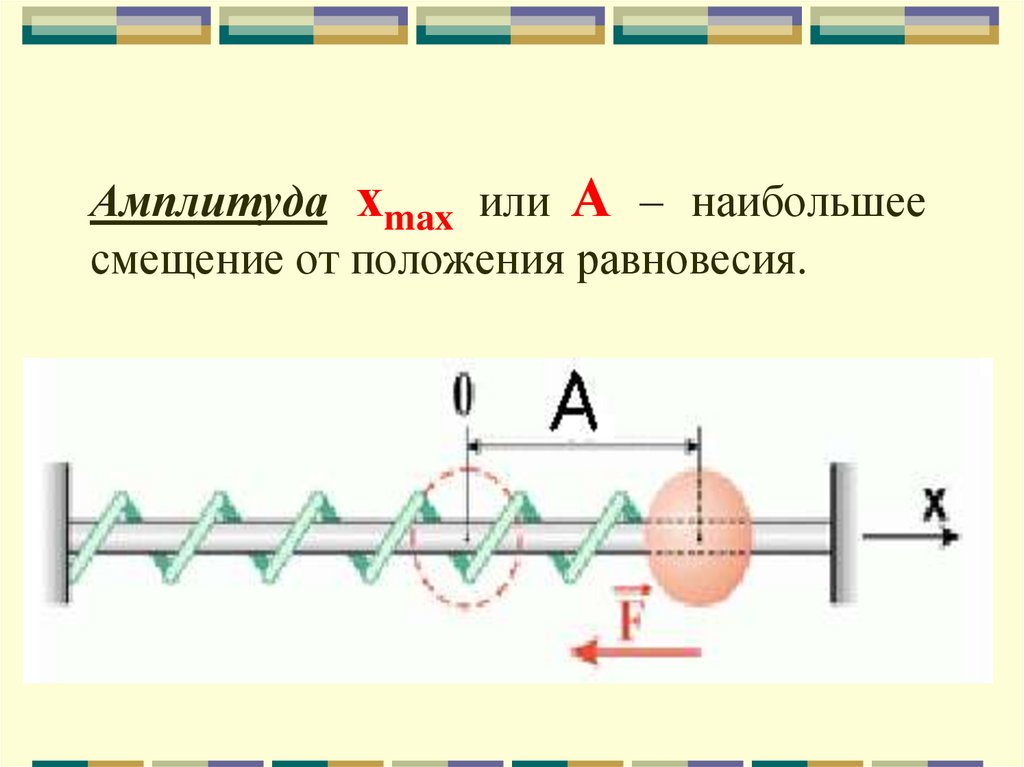
Амплитуда хmax или А – наибольшее
смещение от положения равновесия.

14.

Период Т – время одного полного
колебания. Выражается в секундах.
Частота
- число полных колебаний
за единицу времени.
Выражается в герцах (Гц).
Т
1
N
t

15.

Циклическая (круговая) частота колебаний
– частота , равная числу колебаний ,
совершаемых материальной точкой за 2
секунд.
2
2
Т

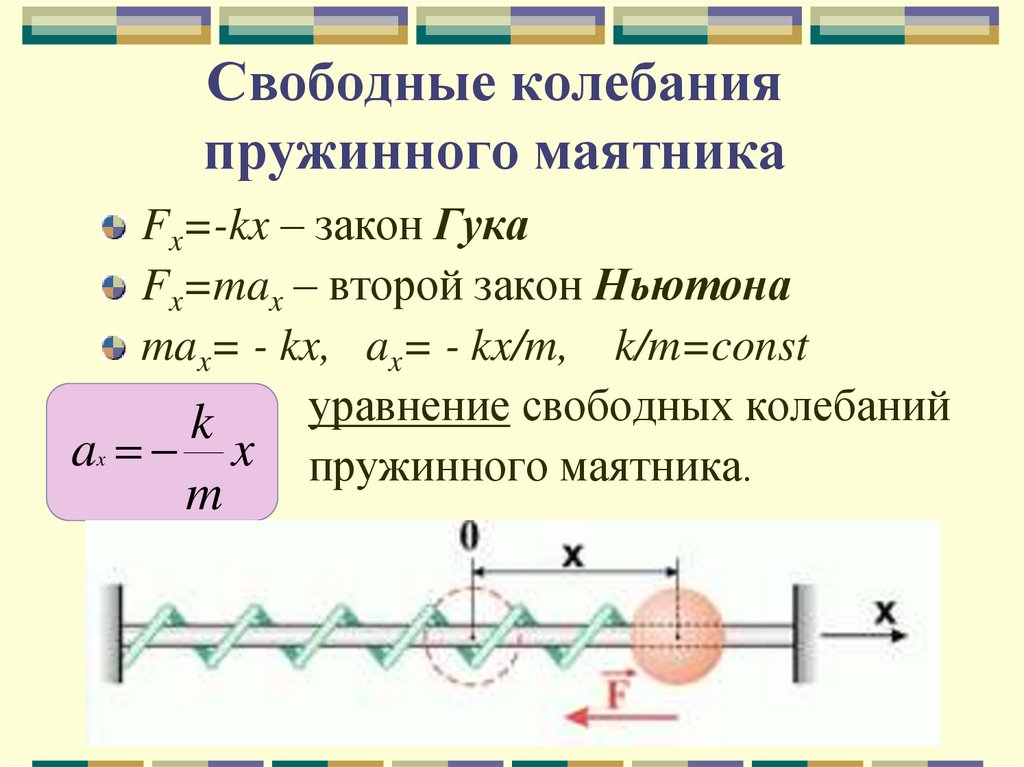
16. Свободные колебания пружинного маятника

Fx=-kx – закон Гука
Fx=max – второй закон Ньютона
max= - kx, ax= - kx/m, k/m=const
уравнение
свободных
колебаний
k
ax x пружинного маятника.
m

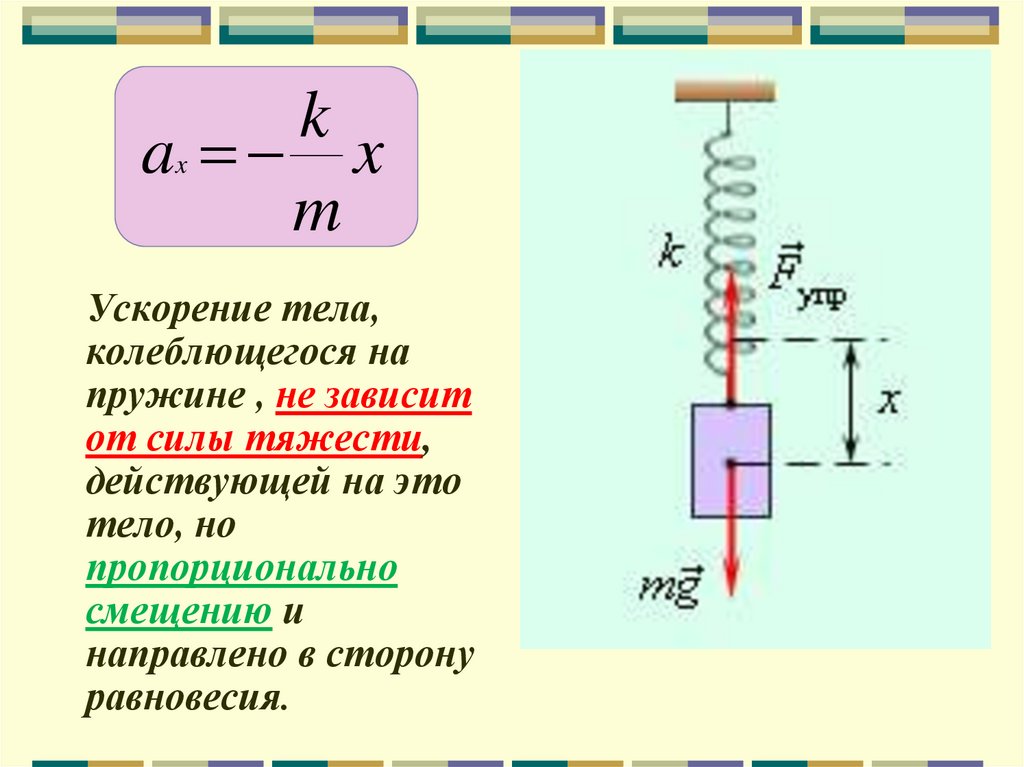
17.

k
a x
m
x
Ускорение тела,
колеблющегося на
пружине , не зависит
от силы тяжести,
действующей на это
тело, но
пропорционально
смещению и
направлено в сторону
равновесия.

18. Гармонические колебания

Колебания, при которых изменения
физических величин происходят по
закону косинуса или синуса
x x mcos(ω t 0 )
Выражение, стоящее под знаком
cos или sin, наз. фазой колебания:
t 0
Фаза колебания измеряется в радианах и
определяет значение смещения
(колеблющейся величины) в данный момент
времени.
Амплитуда колебания Хm зависит
только от начального отклонения

19. Скорость при гармонических колебаниях

Согласно определению скорости, скорость – это производная
от координаты по времени
v x (x msin(ω t φ0 )) x mωcos(ωt φ0 ) x mωsin(ωt φ0 π )
2
Таким образом, мы видим, что скорость при гармоническом
колебательном движении также изменяется по
гармоническому закону, но колебания скорости опережают
колебания смещения по фазе на /2.
Величина vm xm - максимальная скорость
колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при
гармоническом колебании имеем: v v mcos(ω t φ0 )

20. Ускорение при гармонических колебаниях

Ускорение – это производная от скорости по времени:
a v (x ) x
a v (v m cos(ω t φ 0 )) (x m ωcos(ωt φ 0 ))
x m ω 2 sin( ω t φ 0 ) x m ω 2 sin( ω t φ 0 π)
Ускорение при гармоническом колебательном движении
также изменяется по гармоническому закону, но колебания
ускорения опережают колебания скорости на /2 и колебания
смещения на (в противофазе)
a amsin( ω t φ0 )
Величина x mω a m - максимальное ускорение (амплитуда
ускорения).
2

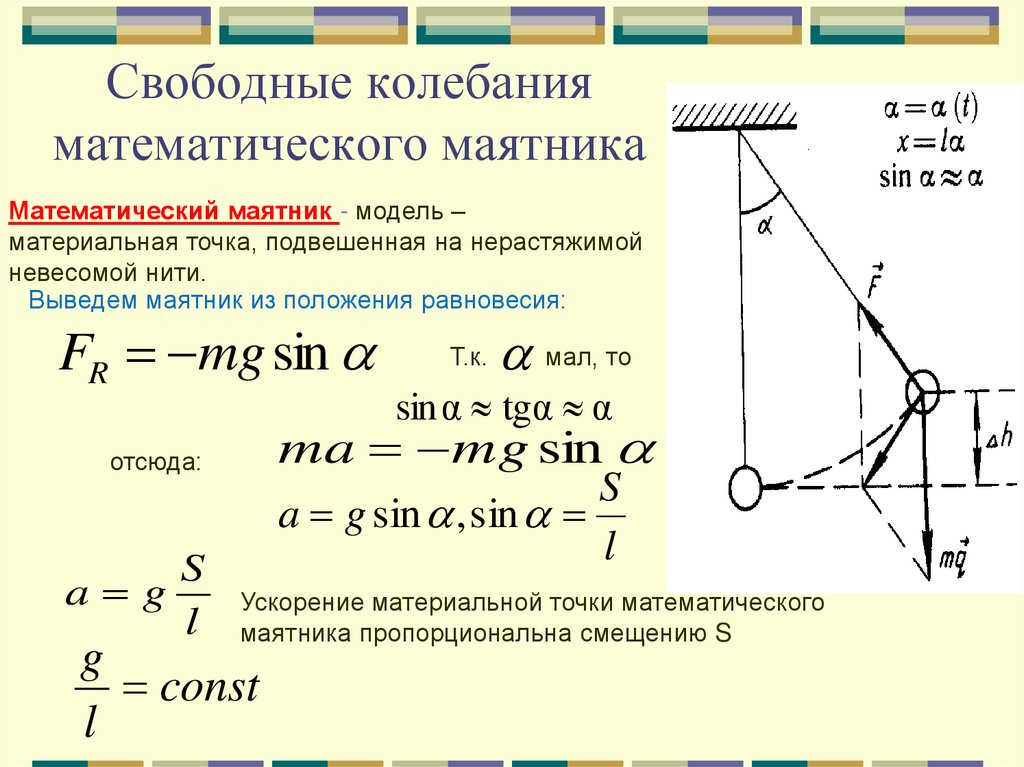
21. Свободные колебания математического маятника

Математический маятник - модель –
материальная точка, подвешенная на нерастяжимой
невесомой нити.
Выведем маятник из положения равновесия:
FR mg sin
мал, то
sin α tgα α
ma mg sin
S
a g sin , sin
отсюда:
S
a g
l
Т.к.
l
Ускорение материальной точки математического
маятника пропорциональна смещению S
g
const
l

22. Период колебания

Сравним полученное уравнение
s
g
a g x
l
l
с уравнением колебательного движения
Видно, что
ω
2
g
l
Период колебаний T
или ω
2 π 2π
ω
g
l
2
a x x
g - циклическая частота при колебаниях
l математического маятника.
или
l
T 2π
g
Период колебаний математического маятника
не зависит от массы тела!

23. Свободные колебания пружинного маятника

В вертикальном положении на груз на пружине
действуют сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина растягивается
на х1, а затем мы отклоняем его от этого положения
наТогда
х.
согласно второму закону
Ньютона, учитывая знаки проекций,
получим: ma k x x mg
Но , x1
тогда: .
mg
k
1
ma k |
mg
x| mg k |x|
k
Или ma kx
ускорение тела,
колеблющегося на пружине, не зависит от
силы тяжести, действующей на это тело. Сила
тяжести только приводит к изменению
положения равновесия.
Ускорение тела, колеблющегося на
k
Выразим ускорение:
a x пружине, не зависит от силы
m
тяжести, действующей на это тело,
но пропорционально смещению

24. Период колебания

k Сравним полученное уравнение с уравнением
x колебательного движения .
Т.к. a
2
m
a x x
k - циклическая частота при
k
2
Видно, что
или
m
m колебаниях пружинного маятника.
Период колебаний
2
2
T
k
m
или
T 2
m
k