Законы сохранения. Работа и энергия. (Тема 3)

1. ТЕМА III. РАБОТА И ЭНЕРГИЯ

§1. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

2. 1. РАБОТА СИЛЫ

Физическая величина, равная скалярному произведению действующей
на тело силы F , на совершённое под действием этой силы
элементарное перемещение dS , называется работой силы:
dA F dS ,
dA FdS cos ,
A 1 Н 1 м 1 Дж ( Джоуль).
Если на конечном перемещении S
величина и направление силы,
действующей на тело, не меняется,
то выражение для работы принимает
более простой вид:
A F S FS cos Fs S .
В случае переменной силы работа
вычисляется как интеграл вдоль траектории:
Поскольку работа – это интеграл,
2
A12 FdS . то её величина численно равна
площади под графиком проекции
1
силы в зависимости от перемещения.

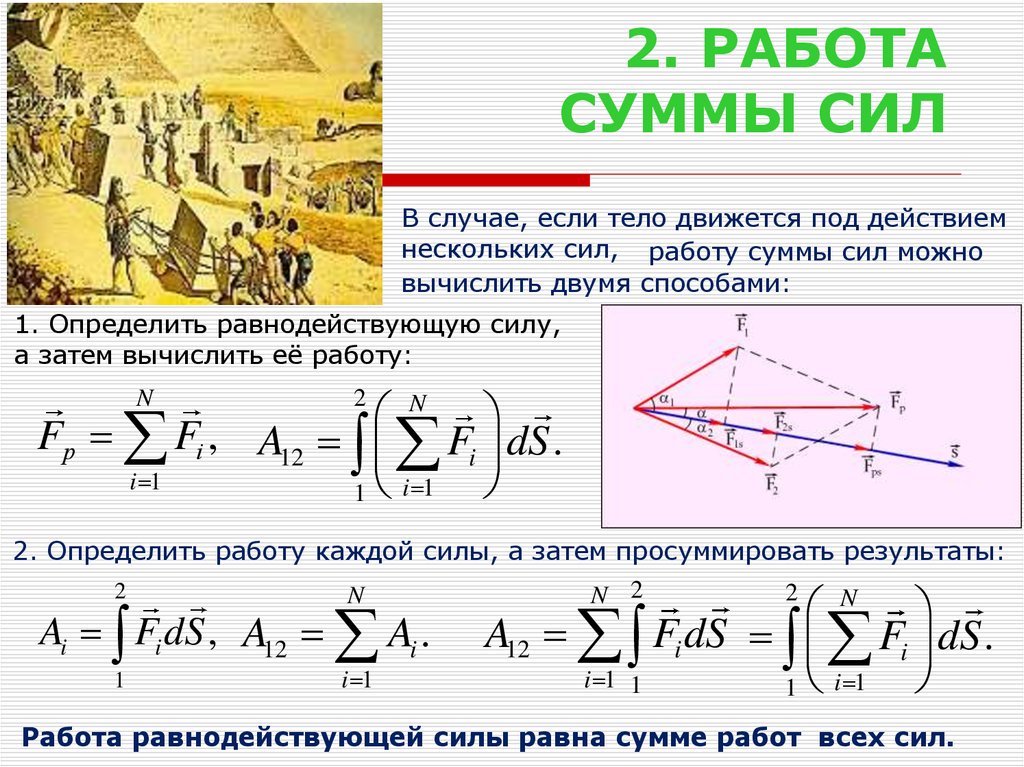
3. 2. РАБОТА СУММЫ СИЛ

В случае, если тело движется под действием
нескольких сил, работу суммы сил можно
вычислить двумя способами:
1. Определить равнодействующую силу,
а затем вычислить её работу:
N
Fр Fi , A12 Fi dS .
i 1
1 i 1
N
2
2. Определить работу каждой силы, а затем просуммировать результаты:
2
2
N
N 2
N
Ai Fi dS , A12 Ai .
1
i 1
A12 Fi dS Fi dS .
i 1 1
1 i 1
Работа равнодействующей силы равна сумме работ всех сил.

4. 3. МОЩНОСТЬ

Работа, совершаемая
в единицу времени
называется мощностью.
Средняя мощность:
A
Pc N c
.
t
Мгновенная мощность:
dA FdS
P
FV FV cos .
dt
dt
t2
dA FVdt A FVdt.
Дж
1 Вт.
P 1
с
t1

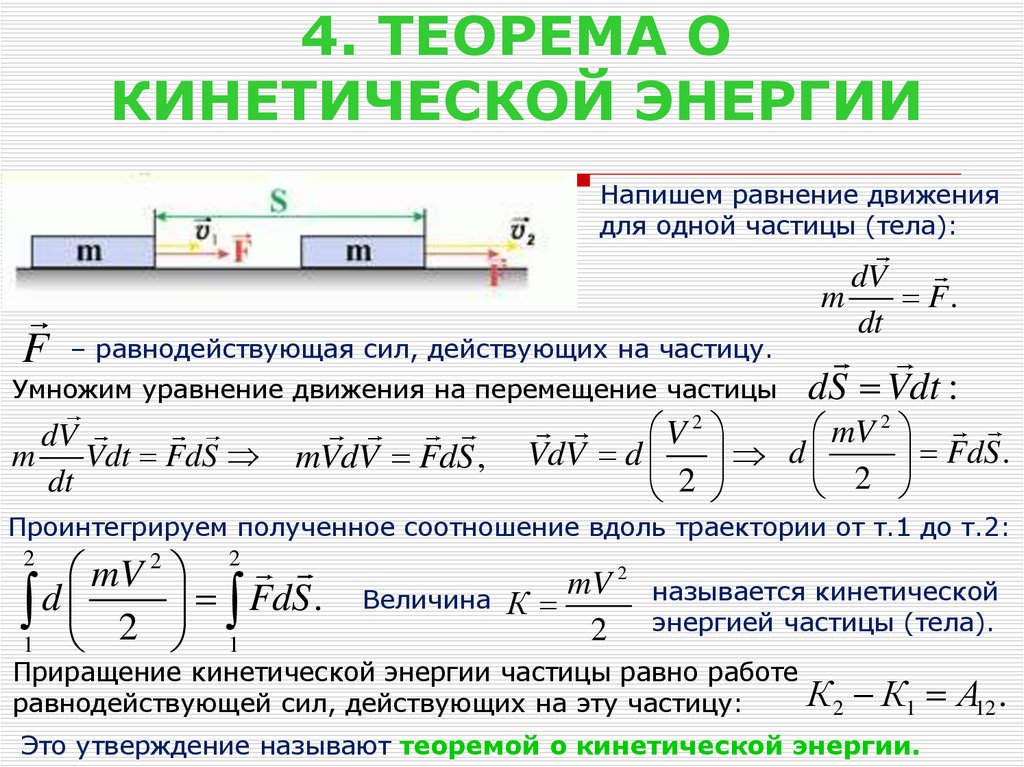
5. 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Напишем равнение движения
для одной частицы (тела):
F
– равнодействующая сил, действующих на частицу.
Умножим уравнение движения на перемещение частицы
dV
m
Vdt FdS
dt
mVdV FdS ,
dV
m
F.
dt
dS Vdt :
mV 2
V 2
FdS .
VdV d d
2
2
Проинтегрируем полученное соотношение вдоль траектории от т.1 до т.2:
mV 2 2
1 d 2 1 FdS .
2
Величина
mV 2
К
2
называется кинетической
энергией частицы (тела).
Приращение кинетической энергии частицы равно работе
равнодействующей сил, действующих на эту частицу:
К 2 К1 А12 .
Это утверждение называют теоремой о кинетической энергии.

6. 5. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ И ИМПУЛЬС ТЕЛА

Из теоремы о кинетической энергии К 2 К1 А12 ( К А) следует,
что кинетическая энергия выражается в тех же единицах что и работа,
то есть в Джоулях.
Кинетическая энергия частицы может быть выражена через его импульс:
mV 2
Wk K
2
m 2V 2
K
,
2m
p mV
p2
K
.
2m
Импульс частицы также можно выразить через её кинетическую энергию:
p 2mK p 2mK ;
2

7. §2. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

8. 1. СИЛОВОЕ ПОЛЕ

Силовое поле (физическое поле) – форма материи.
Представляет собой некоторую область пространства,
в которой физические объекты испытывают силовое воздействие.

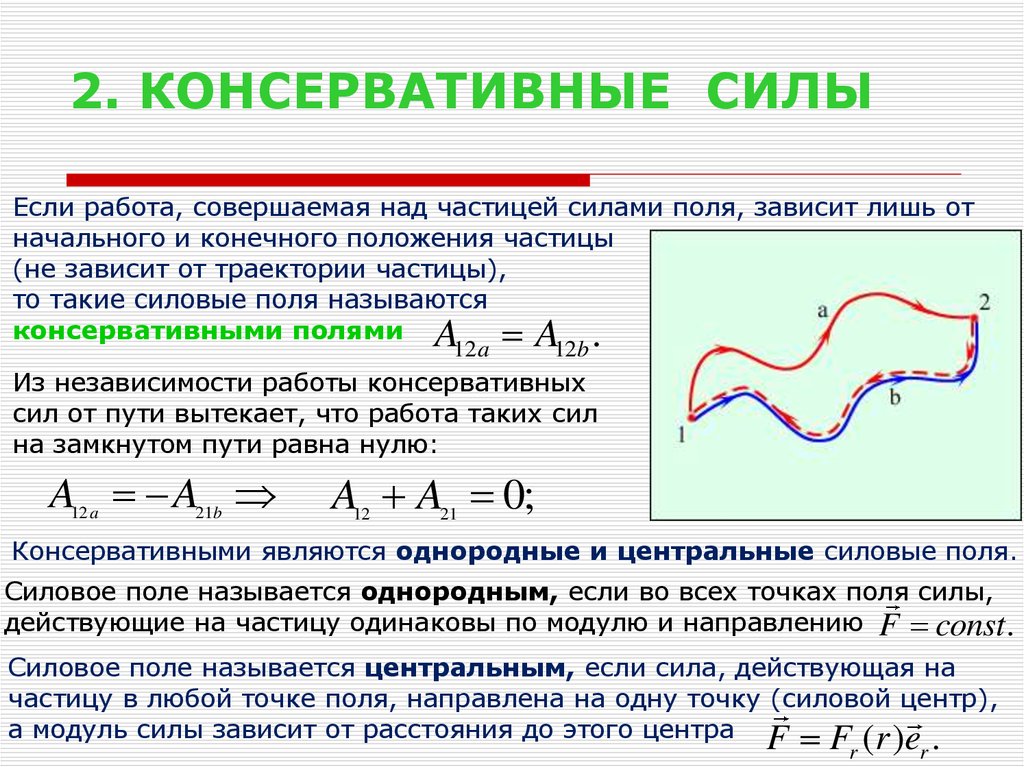
9. 2. КОНСЕРВАТИВНЫЕ СИЛЫ

Если работа, совершаемая над частицей силами поля, зависит лишь от
начального и конечного положения частицы
(не зависит от траектории частицы),
то такие силовые поля называются
консервативными полями A
A .
12 a
12b
Из независимости работы консервативных
сил от пути вытекает, что работа таких сил
на замкнутом пути равна нулю:
A12 a A21b
A12 A21 0;
Консервативными являются однородные и центральные силовые поля.
Силовое поле называется однородным, если во всех точках поля силы,
действующие на частицу одинаковы по модулю и направлению F const.
Силовое поле называется центральным, если сила, действующая на
частицу в любой точке поля, направлена на одну точку (силовой центр),
а модуль силы зависит от расстояния до этого центра F F ( r )e .
r
r

10. 3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

В случае, когда работа сил поля не зависит от пути, а зависит лишь от
начального и конечного положения частицы (консервативные силы),
каждой точке поля можно сопоставить некоторую функцию П ( x, y, z )
такую, что разность значений этой функции в начальной и конечной
точках траектории, будет определять работу сил поля
при переходе частицы из начальной точки в конечную: A12 П1 П2 .
Функция П ( x, y, z ) измеряется в тех же единицах,
что и работа силы, то есть Джоулях.
Её называют потенциальной энергией
частицы во внешнем поле сил.
Потенциальной энергией частицы
в консервативном силовом поле
называется такая функция координат
частицы, убыль которой равна работе
сил поля над этой частицей при её
перемещении из начальной точки траектории в
конечную: П П A ( П П ) A П A .
1
2
12
2
1
12
12

11. 4. НЕОДНОЗНАЧНОСТЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ

Физический смысл имеет не сама потенциальная энергия, а её убыль,
равная работе сил поля над частицей при перемещении
этой частицы из начальной точки траектории в конечную: П1 П2 A12 .
Для расчёта потенциальной энергии частицы
в конкретной точке поля необходимо выбрать
ту точку поля, в которой потенциальная энергия
частицы принимается равной нулю. Пусть
П2 0 П1 U (1) А10 , П ( x, y, z ) A0 .
Потенциальная энергия частицы в данной точке поля равна работе,
которую совершают силы поля над частицей при её перемещении
из данной точки поля в ту точку, для которой
потенциальная энергия принята равной нулю.
Ясно, что величина потенциальной
x0 , y0 , z0
частицы в данной точке
A0
FdS . энергии
зависит от выбора точки с нулем
x, y,z
потенциальной энергии.
В этом состоит неоднозначность потенциальной энергии.

12. 5. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЧАСТИЦЫ В ПОЛЕ СИЛЫ ТЯЖЕСТИ

Сила тяжести в каждой точке имеет
одинаковый модуль и направление – вниз.
2
2
1
1
F mg A12 mgdS mg cos dS ,
2
cos dS dh A12 mg dh
1
A12 mg (h2 h1 ) mg (h1 h2 ).
Сравнивая полученное выражение с
определением потенциальной энергии
П1 П2 A12 , получаем выражение
для потенциальной энергии частицы
в поле силы тяжести П mgh,
h
отсчитывается от нулевым уровня.

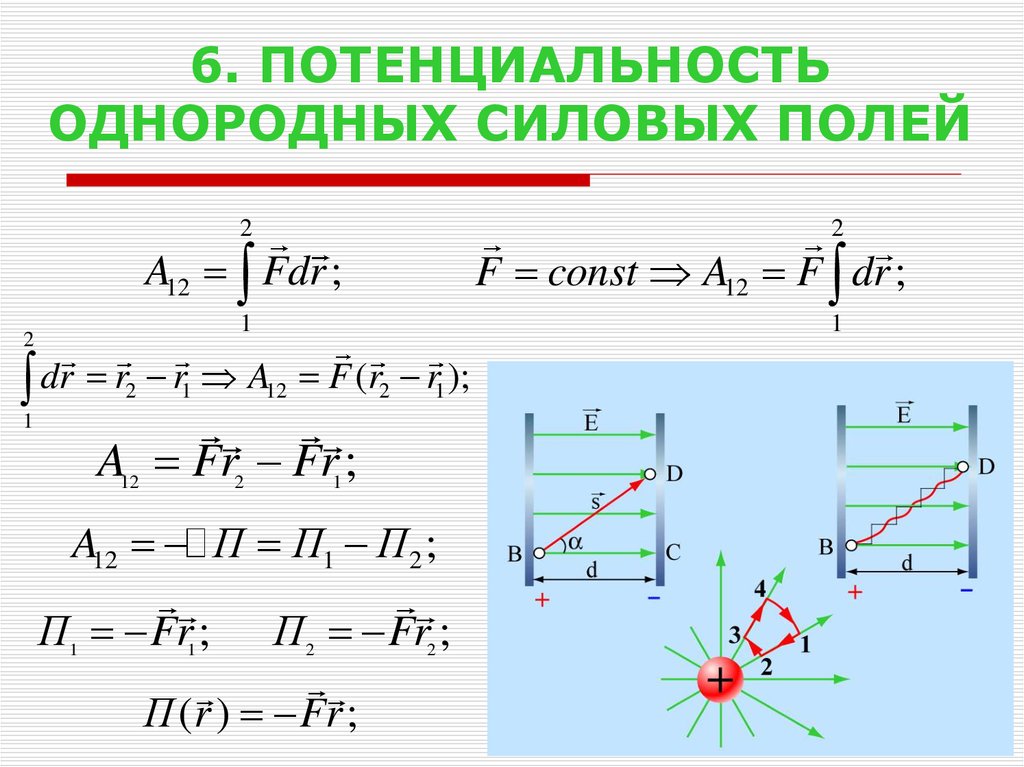
13. 6. ПОТЕНЦИАЛЬНОСТЬ ОДНОРОДНЫХ СИЛОВЫХ ПОЛЕЙ

2
2
A12 Fdr ;
F const A12 F dr ;
1
2
dr r
2
1
r1 A12 F (r2 r1 );
A Fr Fr ;
1
12
2
1
A12 П П1 П2 ;
П Fr ; П Fr ;
П (r ) Fr ;
1
1
2
2

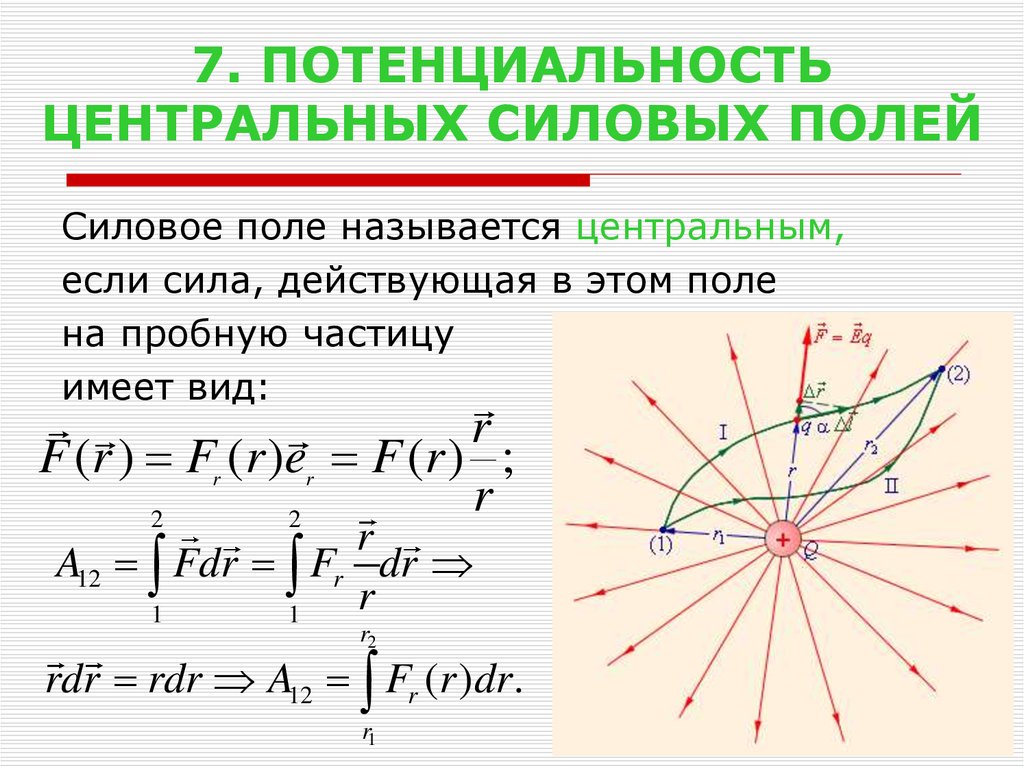
14. 7. ПОТЕНЦИАЛЬНОСТЬ ЦЕНТРАЛЬНЫХ СИЛОВЫХ ПОЛЕЙ

Силовое поле называется центральным,
если сила, действующая в этом поле
на пробную частицу
имеет вид:
r
F ( r ) F ( r )e F ( r ) ;
r
2
2
r
r
r
A12 Fdr Fr dr
r
1
1
r2
rdr rdr A12 Fr (r )dr.
r1

15. 8. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ГРАВИТАЦИОННОГО ВЗАИМОДЕЙСТВИЯ

m1 M ; m m; r12 r ;
mM r
F F (r )
;
r r
2
21
2
mM r
mM
F (r )
;
r r
r
r
2
r2
2
r2
dr
A12 Fr (r )dr mM 2
r
r1
r1
1 1
mM
1
П1 П2 mM mM П (r )
.
r
r r1
r1 r2
r2

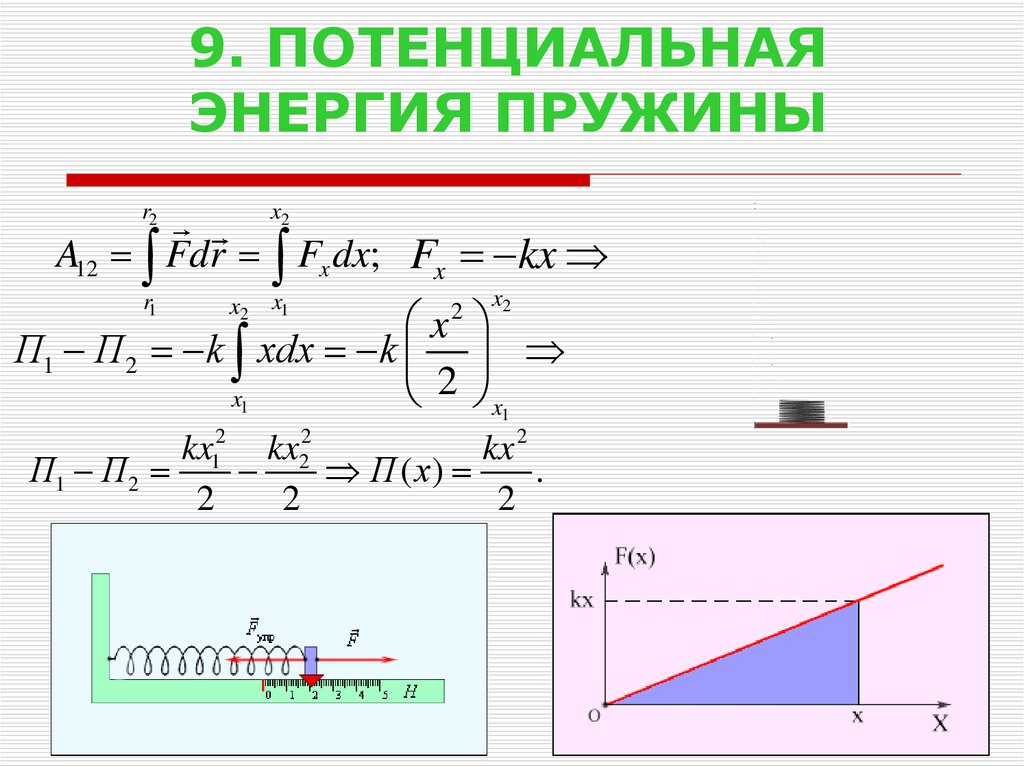
16. 9. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРУЖИНЫ

r2
x2
r1
x2 x1
A12 Fdr Fx dx; Fx kx
x2
x
П1 П2 k xdx k
2 x1
x1
2
kx12 kx22
kx 2
П1 П 2
П ( x)
.
2
2
2

17. 11. СВЯЗЬ МЕЖДУ СИЛОЙ И ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ

A12 П1 П2 A12 ( П2 П1 )
A12 П dA dП.
dA Fdr Fx dx Fy dy Fz dz;
П
П
П
dП
dx
dy
dz.
x
y
z
П
П
П
Fx dx Fy dy Fz dz
dx
dy
dz
x
y
z
П
П
П
Fy
;
Fx
;
Fz
.
y
x
z

18. 12. СИЛА – ГРАДИЕНТ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ

П
П
П
F Fx i Fy j Fz k ; Fx
; Fy
; Fz
x
z
y
П
П
П
F
i
j
k gradП .
y
z
x
grad
i
j
k .
x
y
z
- оператор набла.
i
j k.
x
y
z

19. §3. ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ

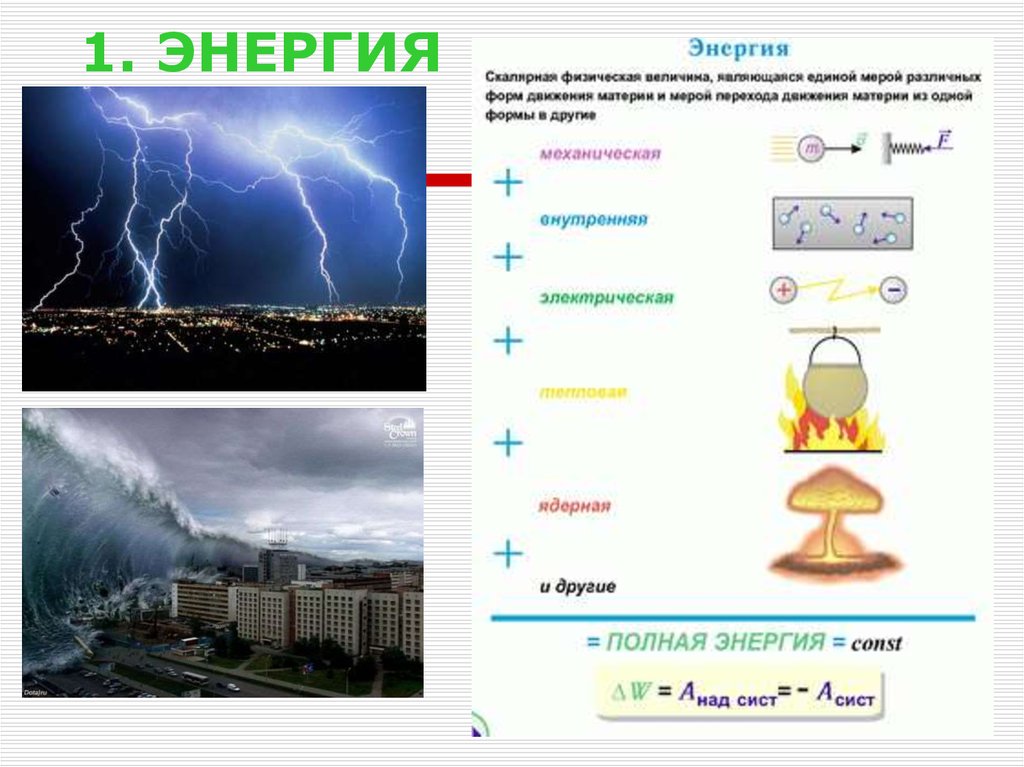
20. 1. ЭНЕРГИЯ

21. 2. ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ ЧАСТИЦЫ

E К П.
W T U.

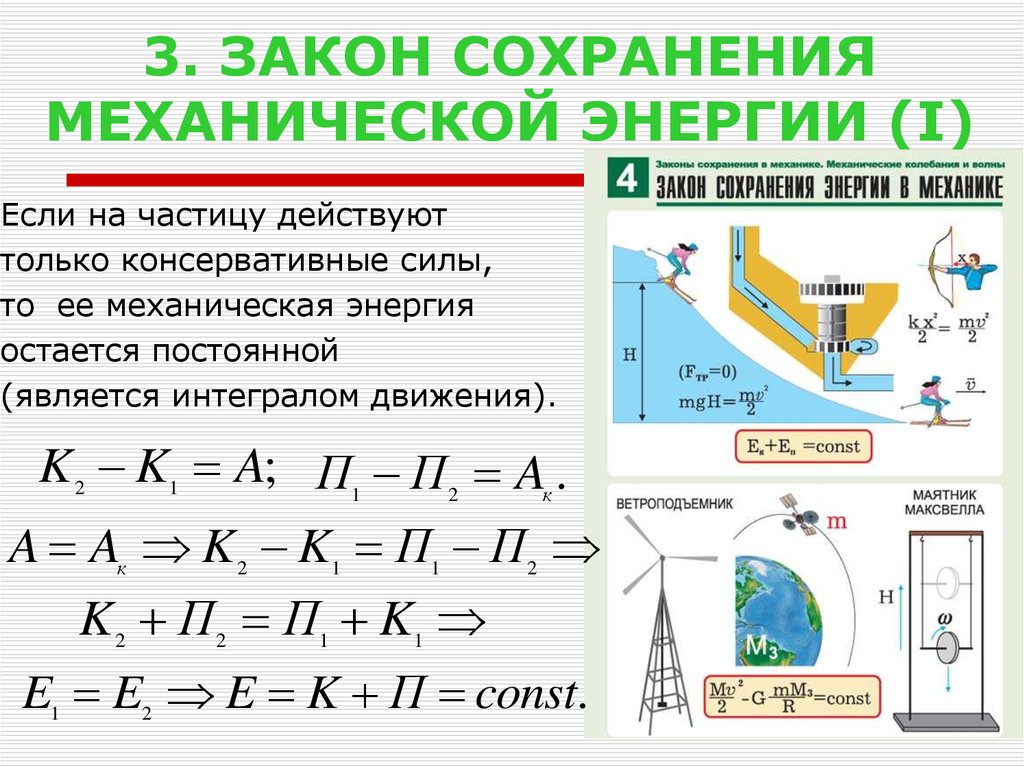
22. 3. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ (I)

Если на частицу действуют
только консервативные силы,
то ее механическая энергия
остается постоянной
(является интегралом движения).
K 2 K1 A; П П A .
A A K K П П
K 2 П2 П1 K1
E E E K П const.
1
к
1
2
2
1
к
2
1
2

23. 4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СИСТЕМЫ ЧАСТИЦ

1
П Пext Пint . Пint П12 П13 П21 П23 П31 П32 .
2
N
N
1 N
Пext Пi ;
Пint
Пij Пij .
i 1
2
i j
i j

24. 5. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ (II)

Полная механическая энергия системы тел,
на которые действуют только консервативные
силы, остается постоянной.
N
N
N
i 1
i 1
i j
E Ki Пi Пij const.

25. 6. НЕКОНСЕРВАТИВНЫЕ СИЛЫ И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ

Aнк W E;
Aнк E2 E1.

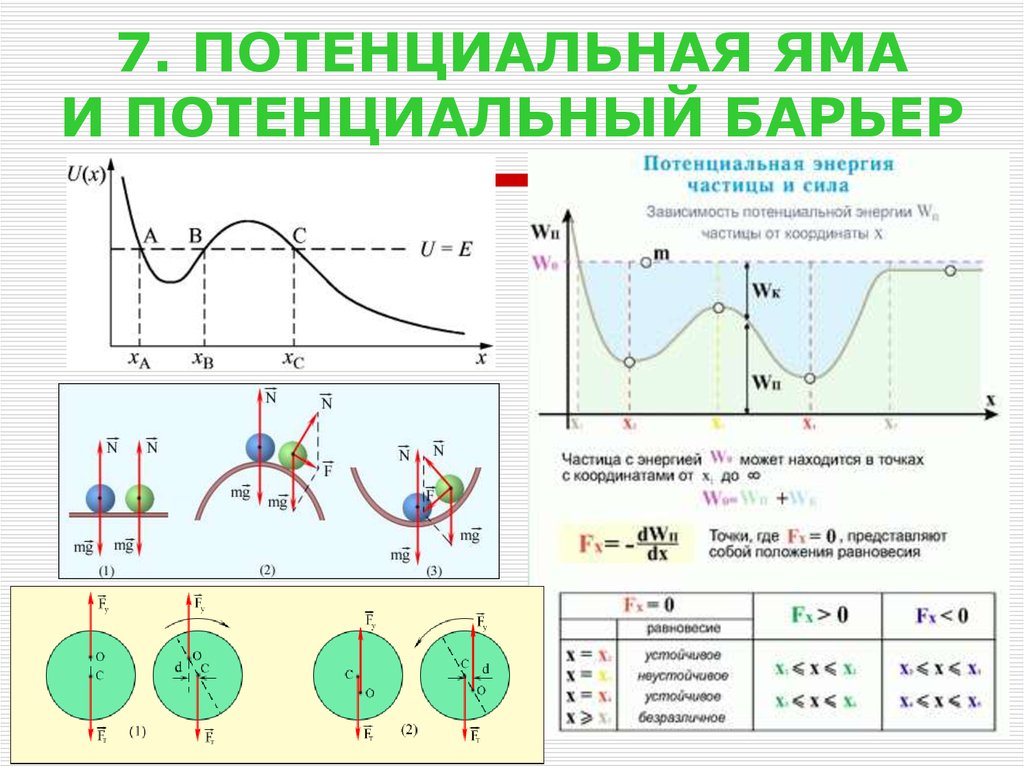
26. 7. ПОТЕНЦИАЛЬНАЯ ЯМА И ПОТЕНЦИАЛЬНЫЙ БАРЬЕР

27. 8. АБСОЛЮТНО НЕУПРУГИЙ УДАР

Абсолютно неупругим называется
такой удар, при котором возникают
только пластические деформации.
m1V1 m2V2 m1 m2 V ; 1 2 .
m1 m2
2
V mV
1 1 m2V2
2
2
2
2 2
2 2
m
m
V
m
V
2
m
m
VV
cos
m
1 2
1 1
1 2 1 2
2V2 ;
2
2 2
m12V12 2m1m2VV
cos
m
1 2
2V2 cos mV
1 1 cos 1 m2V2 cos 2 .
2
2
2
m
m
V
m1V1 m2V2 1
2
Q.
2
2
2

28. 9. АБСОЛЮТНО УПРУГИЙ ЦЕНТРАЛЬНЫЙ УДАР

mV
1 1x m2V2 x mU
1 1x m2U 2 x ;
m1V12x m2V22x m1U12x m2U 22x
.
2
2
2
2
m1 V1x U1x V1x U1x m2 U 2 x V2 x U 2 x V2 x ;
m1 V1x U1x m2 U 2 x V2 x .
V1x U1x V2 x U 2 x U 2 x U1x V1x V2 x
mV
1 1x mU
1 1x m2U1x m2 (V1x V2 x )
2m1V1x m2 m1 V2 x
2m2V2 x m1 m2 V1x
.
U1 x
; U2x
m1 m2
m1 m2

29. 10. ЦЕНТРАЛЬНЫЙ УДАР (ЧАСТНЫЕ СЛУЧАИ)

2m2V2 x m1 m2 V1x
U1 x
;
m1 m2
U2x
2m1V1x m2 m1 V2 x
.
m1 m2
U1x U 2 x ; U1x U 2 x V1x V2 x .
m1 m2 U1x V2 x ; U 2 x V1x .
V2 x 0 U1x 0;
m2
U 2 x V1x .
m1 U 2 x V2 x ;
U1x 2V2 x V1x .
V2 x 0 U1x V1x .

30. 11. НЕЦЕНТРАЛЬНЫЙ УПРУГИЙ УДАР

m1 m2 m;
V2 0.
mV1 mU1 mU 2 V1 U1 U 2 V U1 U 2
2
1
V U 2U1U 2 cos U .
2
1
2
1
2
1
2
2
2
1
2
2
mV
mU
mU
2
2
2
V12 U12 U 22
2U1U 2 cos 0 cos 0 90 .
2