Similar presentations:
Механика. Работа. Кинетическая энергия. Лекция 5
1. I.Механика. Работа. Кинетическая энергия
•В динамике для оценки действия на тело силы вводят величинуработы силы.
dA Fds F ds cos ,
где F - сила, ds - перемещение под действием силы, - угол
между силой и перемещением. При
2
, A 0 , при
2
, A 0 , при
Мощность - работа в единицу времени P
Работа на конечном перемещении равна
2
,A 0.
dA Fds
Fv .
dt
dt
v2
v
dv
ds
v22
v12
A12 Fds m
ds m
dv mvdv m m m ,
dt
dt
2
2
2 v1
1
1
v1
v1
2
Где m v - кинетическая энергия тела. Таким образом, работа
2
2
2
v2
v2
2
равна изменению кинетической энергии (теорема о кинетической
2. I.Механика. Консервативные силы.
энергии).В случае действия нескольких сил, сила F есть их
равнодействующая.
Потенциальная энергия
Консервативные – силы, работа которых по перемещению
тела не зависит от пути перемещения, а зависит от начального и
конечного положения. Кроме контактного взаимодействия
существуют взаимодействия с физическими полями – одной из
форм существования материи. Тело может изменять свойства
окружающего пространства, создавая в нем поле, например,
гравитационное, электрическое и т.д. Задать поле – определить в
каждой точке пространства силу. В гравитационном поле Земли на
любое тело в каждой точке вблизи поверхности действует сила mg .
Работа консервативных сил по замкнутому пути равна нулю
(Рис.11)
3. I.Механика. Консервативные силы. Потенциальная энергия.
а1
2
b
Рис.11
2
При изменении направления
перемещения знак работы меняется на
противоположный. A12 F ( r ) dr A01 A02 U 1 U 2
1
Поле однородно, если в любой
точке силы, действующие на тело
равны по величине и направлению. Если силы не зависят от
времени, то поле стационарно. 2Силы в однородном стационарном
поле консервативны.
A F r dr
12
1
•В центральном поле силы F r направлены в сторону неподвижного центра, зависят от r и в стационарном поле являются консервативными
2
dA F r ds F r dr
A12 F ( r ) dr
1
4. I.Механика. Консервативные силы. Потенциальная энергия.
В поле консервативных сил можно ввести потенциальнуюэнергию, определив ее как взятую с обратным знаком работа по
перемещению материальной точки из начала координат в данную
точку P: U P A0P . С другой стороны работа равна
Таким образом, работа в поле консервативных сил равна изменению потенциальной энергии . Для бесконечно малого перемещения
по осям координат для работы можно написать:
dA Fx dx dU , Fy dy dU , Fzdz dU .
5. I.Механика. Консервативные силы. Потенциальная энергия.
Тогда сила связана с потенциальной энергией следующимсоотношением F dU i dU j dU k gradU ,
dx
где
dy
dz
grad i
j
k
y
z
x
Градиент направлен в сторону максимального увеличения
соответствующей величины.
Закон сохранения энергии.
2
2
v
v
Для материальной точки dA d m dU , d m dU 0
Eкин
U const
2
2
и
Это есть закон сохранения энергии: полная энергия материальной
точки равная сумме кинетической и потенциальной энергий
сохраняется. Этот закон связан с однородностью времени (на оси
времени нет выделенных точек).
6. I.Механика. Закон сохранения энергии
При рассмотрении механической системы необходимоучитывать силы взаимодействия между ее материальными точками.
Если они консервативны, то можно ввести потенциальную энергию
их взаимодействия как потенциальную энергию одной
материальной точки в поле других точек.
Изменение кинетической энергии механической системы
равно работе всех сил (внешних и внутренних), приложенным к ее
материальным точкам, а изменение потенциальной энергии системы
равно работе всех консервативных сил (внутренних и внешних),
взятых с обратным знаком.
Eкин Aконс Aнеконс (U внешн U внутр ) Aнеконс
Изменение механической энергии Eмех ( Eкин U ) Aнеконс ,
где U – сумма потенциальной энергии взаимодействия
материальных точек и потенциальной энергии системы во внешнем
поле. Если неконсервативные силы отсутствуют , то полная энергия
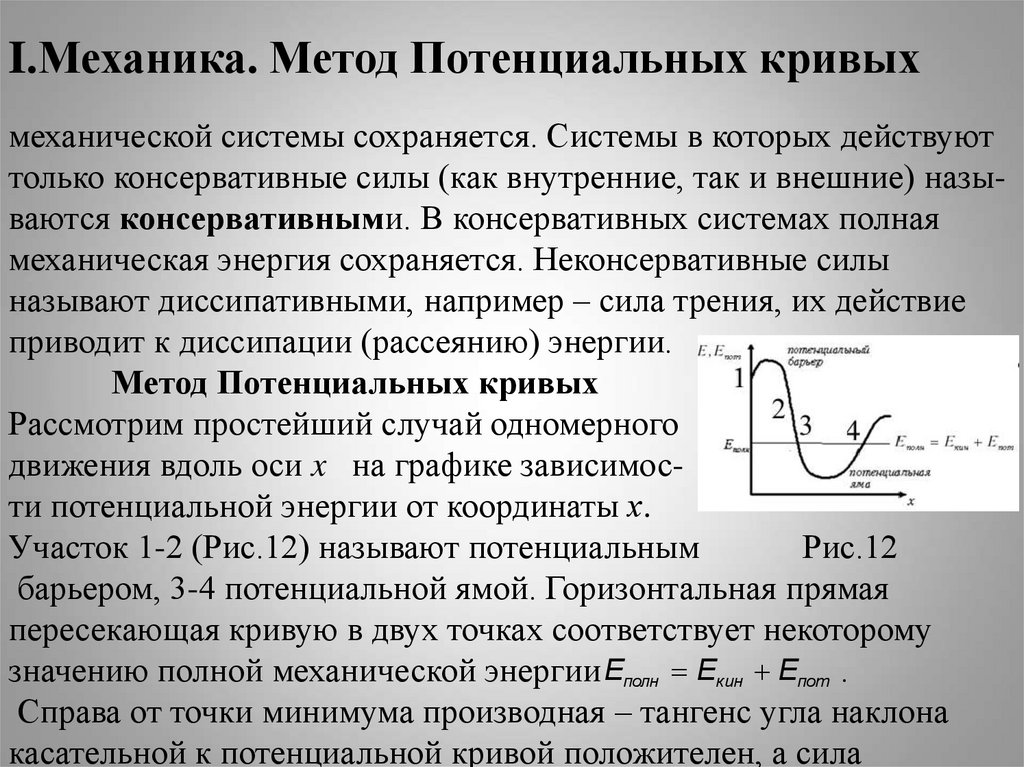
7. I.Механика. Метод Потенциальных кривых
механической системы сохраняется. Системы в которых действуюттолько консервативные силы (как внутренние, так и внешние) называются консервативными. В консервативных системах полная
механическая энергия сохраняется. Неконсервативные силы
называют диссипативными, например – сила трения, их действие
приводит к диссипации (рассеянию) энергии.
Метод Потенциальных кривых
Рассмотрим простейший случай одномерного
движения вдоль оси x на графике зависимости потенциальной энергии от координаты х.
Участок 1-2 (Рис.12) называют потенциальным
Рис.12
барьером, 3-4 потенциальной ямой. Горизонтальная прямая
пересекающая кривую в двух точках соответствует некоторому
значению полной механической энергии Eполн Eкин Eпот .
Справа от точки минимума производная – тангенс угла наклона
касательной к потенциальной кривой положителен, а сила
8. I.Механика. Метод Потенциальных кривых
FdU
dx
отрицательна.
Слева от минимума тангенс угла наклона касательной отрицателен,
а сила положительна. В точке минимума сила равна нулю, т.е. это
есть положение равновесия. При смещении от этой точки вправо
возникает сила возвращающая материальную точку в положение
равновесия. Тот же результат будет и при смещении влево. Поэтому
равновесие в этом случае является устойчивым. Вблизи максимума
потенциального барьера положение равновесия неустойчиво. Пусть
– полная энергия материальной точки. Полная энергия
Eполн Eкин Eпот Eпот . В точках 3 и 4 пересечения прямой полной
энергии с потенциальной кривой полная энергия равна
потенциальной, поэтому движение на участке 3-4 возможно, а вне
этого отрезка, где Eполн Eпот невозможно.
9. I.Механика. Неупругий и упругий удары.
•Пусть два тела движутся вдоль прямой, соединяющей их центры, апосле столкновения движутся вместе. Такой удар называется
неупругим и центральным. Запишем закон сохранения импульса,
m1v1 m2v2 m1 m2 v
где m1, v1 - масса и скорость первого тела, m2, v2 - масса и скорость
второго тела, v - скорость их совместного движения. При неупругом ударе действуют диссипативные силы, поэтому полная энергия
не сохраняется.
Рассмотрим упругий центральный удар двух тел, движущихся вдоль
оси х, и запишем для него законы сохранения импульса и энергии.
m1v1x m2v2x m1u1x m2u2 x
m1v12x m2v22x m1u12x m2u22x
2
2
2
2
Перепишем уравнения. Собрав слева слагаемые, относящиеся к
10. I.Механика. Неупругий и упругий удары.
первому телу, а справа ко второму.m1( v12x u12x ) m2 ( v22x u22x )
m1( v1x u1x ) m2( u2x v2x )
Разделив первое уравнение на второе, получим
( v1x u1x ) ( u2x v2x )
Добавим к нему уравнение m1( v1x u1x ) m2( u2x v2x ) и решив
полученную систему уравнений, получим.
v1
m1 m2 v1x
2m2v2 x
m1 m2
2m1v1x m1 m2 v2 x
v2
m1 m2
Примеры решения задач
Задача 22. Найдите мощность в момент времени t = 2 c,
развиваемую силой, приложенной к материальной точке массой m =.
11. I.Механика. Неупругий и упругий удары.
0,5 кг, движение под действием которой происходит по закону:x = 5 – 3t2 + 5t3–t4 (м).
•Решение. Мощность определяется соотношением P Fx v x
dx
•Скорость равна vx
6t 15t 2 4t 3,
dt
dvx
2
F
m
m
6
30
t
12
t
сила x
, где m – масса точки.
dt
Мощность в момент времени t = 2c равна:
P m( 6t 15t 2 4t 3) ( 6 30t 12t 2) 48 Вт.
Задача 23.
Найдите кинетическую энергию тела,
движущегося из состояния покоя из начала координат вдоль оси x
4
F
5
x
под действием силы
в точке x = 3 м. Потенциальная
x
энергия тела не меняется.
Решение. Работа силы равна изменению кинетической
энергии.
12. I.Механика. Неупругий и упругий удары.
Работа на бесконечно маломx отрезке оси x равна dA=Fx dx, а на4
5 3
конечном участке Eк ин A 5x dx x 0 243Д ж.
0
Задача 24. Найдите потенциальную
энергию камня, брошенного с
поверхности земли под углом = 30 к горизонту, в высшей точке
его траектории, если его кинетическая энергия в начальный момент
равна 40 Дж. Сопротивлением воздуха пренебречь.
Решение. В высшей точке траектории скорость камня равна
v0 cos . В соответствии с законом сохранения энергии потенциальная энергия равна:
mv02 mv02 cos2 mv02
Eпот
(1 cos2 ) 10Дж.
2
2
2
Задача 25. Найдите количество тепла Q, выделившееся при
неупругом столкновении тела массой m1 = 0,4 кг, двигавшегося со
скоростью v = 6 м/с, с неподвижным телом массой m2 = 0,2 кг.
13. I.Механика. Неупругий и упругий удары.
Решение. Запишем законы сохранения энергии и импульса длянеупругого удара: 2m2v0 3m2v,
2m2v02 3m2v 2
Q,
2
2
где – скорость тел после удара. Решая эту систему уравнений,
получим:
2m2v02 3m2v 2 2m2v02 3m2 (2 3v0 ) 2 m2v02
Q
2, 4Д ж
2
2
2
2
3
•Задача 26. Определите кинетическую энергию ствола орудия
вследствие отдачи при вылете снаряда массой m = 25 кг с кинетической энергией 140 кДж, если масса ствола орудия M = 175 кг.
Решение. Из закона сохранения импульса следует, что mv M V
и V mv , где – скорость снаряда, V –скорость ствола.
M
Кинетическая энергия ствола после выстрела равна:
14. I.Механика. Неупругий и упругий удары.
M V 2 M m2v 2m mv 2
20к Дж.
2
2
2M
M 2
Задача 27. Шар массой 3m, движущийся со скоростью v0 = 10
м/с, испытывает упругое центральное соударение с покоящимся
шаром массой m. Найдите скорость первого шара после удара.
Решение. Запишем законы сохранения импульса и энергии для
этого упругого удара: 3mv 3mv mv ,
0
1
2
3mv02 3mv12 mv22
2
2
2
где v2– скорость второго шара после удара.
Соберем в левой части уравнений слагаемые, относящиеся к
первому шару:
15. I.Механика. Неупругий и упругий удары.
3m( v0 v1) mv2,3m( v02 v12 ) mv22
.
2
2
Разделив второе уравнение на первое, получим v0 v1 v2 и
система уравнений примет вид: 3( v v ) v ,
0
1
2
v0 v1 v2
.
1
v
v0 5 м/с.
Решая эту систему уравнений, получим 1
2
Задача 28. . Потенциальная энергия частицы имеет вид: Ер = 2x3
+ 3y2 – z5(Дж). Найдите величину силы, действующей на частицу,
когда она находится в точке с координатами (2,3,1).
• Решение. Сила определяется следующим соотношением:
•Откуда
н.
16. I.Механика. Неупругий и упругий удары.
Задача 29. Частица находится в центральном поле сил, где еепотенциальная энергия зависит от расстояния до центра поля по
закону: Ер = a/r2 – b/r, где a = 3∙10–33 Дж∙м2 , b = 6·10–24 Дж∙м.
Найдите расстояние r0, соответствующее равновесному положению частицы.
Решение. В положении равновесия сила, действующая на
частицу равна нулю:
, откуда положению
равновесия соответствует координата
нм.
• Задача 30. Найдите, сколько процентов от первоначальной
кинетической энергии
тела, брошенного вертикально вверх с
начальной скоростью =30 м/с, составляет его кинетическая
энергия
на высоте 15 м. Сопротивление воздуха не учитывать.
Решение. В соответствии с законом сохранения энергии:
, где Eпот- конечная потенциальная энергия.
17. I.Механика. Неупругий и упругий удары.
, что составляетот первоначальной
кинетической энергии.
















 physics
physics








