Кинетическая энергия

1.

Если сила имеет постоянные величину и направление, то в
результате получится формула
2
A FS dS FS S F S cos
1
Если сила и направление перемещения образуют острый
угол (cos α >0), работа положительна. Если угол α - тупой
(cos α <0), работа отрицательна. При
работа равна 0.
2
Единица работы – джоуль (Дж). 1 Дж – работа, совершаемая
силой 1 Н на пути 1м (1 Дж=1Н∙1м ).

2.

A
N .
t
dA
N
dt
dr
N F
F .
dt

3. Кинетическая энергия

Кинетическая энергия – это
движущегося тела.
механическая энергия
dr
То есть работа силы идет на приращение некоторой величины
(стоящей в скобках). Эту величину называют кинетической
энергией.
Таким образом, кинетическая энергия это механическая энергия,
которой обладает тело массой m, движущееся со скоростью υ.

4.

m 22 m 12
A Fdr m d
K 2 K1.
2
2
1
1
2
2
Если система замкнута, то F внеш. 0 и F 0, тогда и
m 2
d
0.
2
Если
полный
дифференциал
некоторой
функции,
описывающей поведение системы равен нулю, то эта функция
может служить характеристикой состояния данной системы.

5.

Функция состояния системы, определяемая только
скоростью ее движения, называется кинетической энергией.
m 2
K
.
2
(1)
Кинетическая энергия системы есть аддитивная величина.
mi i2
K
.
2
i 1
n
Связь кинетической энергии с импульсом p.
m 2 m m2 2
2 m 2m
p2
K
.
2m
(2)

6. Консервативные силы и системы

Кроме
контактных
взаимодействий,
наблюдаются
взаимодействия между телами, удаленными друг от друга.
Подобное взаимодействие осуществляется посредством
физических полей (особая форма материи).
Каждое тело создает вокруг себя поле, которое проявляет
себя именно воздействием на другие тела.
Силы, работа которых не зависит от пути, по которому
двигалось тело, а зависит от начального и конечного положения
тела называются консервативными.
Обозначим A – работа консервативных
сил, по перемещению тела из т. 1 в т. 2

7.

A1a 2 A1b 2 A1l 2 A12 .
Изменение направления движения на противоположное –
вызывает изменение знака работы консервативных сил. Отсюда
следует, что работа консервативных сил вдоль замкнутой
кривой равна нулю:
Fdr A A A A 0
12
21
12
S
F
12

8.

Если циркуляция какого-либо вектора силы равна нулю,
то эта сила консервативна.
Консервативные силы: сила тяжести, электростатические
силы, силы центрального стационарного поля.
Неконсервативные силы: силы трения, силы вихревого
электрического поля.
Консервативная система – такая, внутренние силы которой
только консервативные, внешние – консервативны и
стационарны.
Работа по подъему тела массы m на
высоту h, равна:
A mgh
21
С другой стороны
A mgl cos α mgh
2 '1

9. Потенциальная энергия

Если на систему материальных тел действуют
консервативные силы, то можно ввести понятие
потенциальной энергии.
• Работа, совершаемая консервативными силами при
изменении конфигурации системы, то есть при изменении
положения тел относительно системы отсчета, не зависит
от того, как было осуществлено это изменение. Работа
определяется
только
начальной
и
конечной
конфигурациями системы:
A12 U1 U 2 .
•Здесь
потенциальная энергия U(х,у,z) – функция
состояния системы, зависящая только от координат всех
тел системы в поле консервативных сил.
•Итак, K – определяется скоростью движения тел системы,
а U – их взаимным расположением.

10.

Связь между потенциальной энергией и
силой
Пространство, в котором действуют консервативные силы,
называется потенциальным полем.
Каждой точке потенциального поля соответствует
некоторое значение силы F, действующей на тело, и
некоторое значение потенциальной энергии U. Значит, между
силой F и энергией U должна быть связь.
Так как
A dU
A Fdr dU
dU
F
er .
dr

11.

Проекции вектора силы на оси координат:
U
Fx
;
x
U
Fy
;
y
U
Fz
.
z
Вектор силы можно записать через проекции
U
U
U
F
i
j
k
y
z
x
F gradU ,
где
(3)
grad i
j k.
x
y
z
Градиент – это вектор, показывающий направление
наибыстрейшего увеличения функции. Т.к. в формуле стоит
знак «минус», то F направлен в сторону наибыстрейшего
уменьшения U.

12. Лекция №5

Курс лекций по Физике 1
Сегодня: понедельник, 16 октября 2023 г.
ЛЕКЦИЯ №5
Тема:
Закон сохранения импульса. (ЗСИ)
Закон сохранения механической
энергии. (ЗСЭ)

13. Движение центра масс

Центр инерции или центр масс системы материальных
точек называют такую точку С, радиус-вектор которой:
n
m r
rc i n1
i i
m
•где m
i 1
n
1 n
mi ri ,
m i 1
(1)
i
m – общая масса системы, n – число точек системы.
i 1
i
Центр масс С системы тел

14.

Величина
pi mi υi
является первым динамическим
параметром частицы и называется
импульсом.
Соответственно величину
Z
K
n
PC mVC mi i
i 1
называют импульсом центра масс.
rc
O
X
Таким образом, связь импульса PC со скоростью VC такая же,
как для материальной точки с массой m (масса системы)
Y

15.

dpc
F
dt
– Скорость изменения импульса системы
тел равна главному вектору всех внешних сил,
действующих на эту систему.
Это уравнение называют основным уравнением динамики
поступательного движения системы тел.
• Так как импульс системы pС mVC, то
d
mVC F
dt
• Отсюда
можно записать основное уравнение динамики
поступательного движения системы тел в виде:
mac F
• Здесь
ac – ускорение центра инерции.

16.

mac F
Центр
механической
системы
движется
как
материальная точка, масса которой равна массе всей
системы, и на которую действует сила, равная главному
вектору внешних сил, приложенных к системе.
• На основании третьего закона Ньютона, силы, действующие
на тела системы со стороны других тел системы (внутренние
силы), взаимно компенсируют друг друга. Остаются
только внешние силы.

17. Теорема о движении центра масс

Рассмотрим подробнее силы, действующие на частицы
механической системы
F1i
m2
Силы, действующие на каждую
точку системы, разобьем на два типа
m3
n
– внутренние силы, a 1
F13
m1
F
c
i
внеш
m i 1
F12
– результирующая всех внешних сил.
mi
(F1)внеш
В общем виде:
n 1
Fi Fik Fi вн
k 1
Fik 0
i ,k
Теорема о движении центра масс:
Если система находится во внешнем стационарном и
однородном поле, то никакими действиями внутри системы
невозможно изменить движение центра масс системы.

18. Изотропность и однородность пространства и времени

• Совокупность материальных точек (или тел) называется
механической системой.
• Однородность
пространства означает, что
пространства одинаковы во всех точках. (ЗСИ)
свойства
• Изотропность
свойства
во всех
пространства означает, что
пространства в каждой точке одинаковы
направлениях. (ЗСМИ)
• Однородность
времени означает, что
протекание
физических явлений (в одних и тех же условиях) в разное
время их наблюдения одинаково. (ЗСЭ)

19. Закон сохранения импульса

Тела, входящие в систему, могут взаимодействовать как
между собой, так и с телами, не принадлежащими системе.
• Внутренние
силы – силы взаимодействия между
материальными точками, входящими в механическую
систему:
• Внешние силы – силы, которые действуют на систему со
стороны тел, не входящих в систему.

20. Закон сохранения импульса

Механическая система называется замкнутой (или
изолированной), если на неё не действуют внешние
силы, т.е. она не взаимодействует с внешними телами.
Строго говоря, каждая реальная система тел всегда не
замкнута, т.к. подвержена, как минимум воздействию
гравитационных сил. Однако если внутренние силы гораздо
больше внешних, то такую систему можно считать
замкнутой (например – Солнечная система).
• Для замкнутой системы равнодействующий вектор
внешних сил тождественно равен нулю:
dpc
F 0,
dt

21.

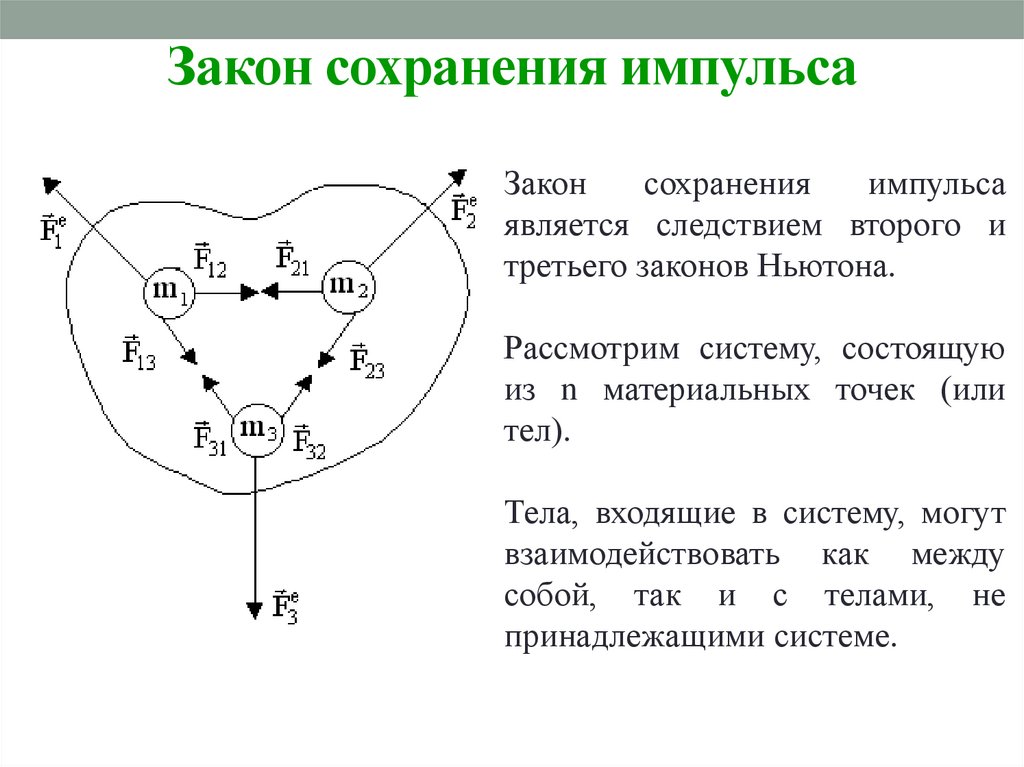
Закон сохранения импульса
Закон
сохранения
импульса
является следствием второго и
третьего законов Ньютона.
Рассмотрим систему, состоящую
из n материальных точек (или
тел).
Тела, входящие в систему, могут
взаимодействовать как между
собой, так и с телами, не
принадлежащими системе.

22.

Пусть на каждое тело массой mi действуют
e
внутренние силы Fik и внешние силы Fi ; тело
приобретает ускорение.
Запишем второй закон Ньютона для каждого
тела:
e
d
m1 1 F12 F13 ...... F1
dt
e
d
m2 2 F21 F23 ...... F2
dt- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - -
e
d
mn n Fn1 Fn2 ...... Fn
dt

23. Складываем эти уравнения. Так как по третьему закону Ньютона

Fik Fki
то сумма всех внутренних сил равна 0.
Имеем
n
n
e
d
mi i
Fi
dt
i 1
i 1
n
mi i = P – импульс системы тел,
Здесь
e e i 1
Fi F - равнодействующая всех внешних сил
n
i 1

24. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на

систему:
dP e
F
dt
Рассмотрим замкнутую систему (т.е. внешние
силы отсутствуют). Тогда
dP
т.е.
0
P
const
dt

25.

n
отсюда
pc mi c const.
i 1
Это есть закон сохранения импульса: импульс замкнутой
системы не изменяется во времени.
Векторная сумма количества движения или полный импульс
замкнутой системы остается постоянным при любых
взаимодействиях между телами этой системы.
• Отметим, что закон сохранения импульса выполняется и для
незамкнутой системы, если геометрическая сумма всех внешних
сил равна 0.
Закон сохранения импульса является одним из основных законов
природы. Он был получен как следствие законов Ньютона, но он
справедлив и для микрочастиц и для релятивистских скоростей,
когда υ ≈ c.

26.

Если система не замкнута, но главный вектор внешних сил
F 0
то
p сист. const,
как если бы внешних сил не было (например, прыжок из
лодки, выстрел из ружья или реактивное движение).

27.

dP
закон
сохранения
импульса
в
0
дифференциальной форме
dt
Из закона сохранения импульса вытекает два
важных следствия закон движения центра инерции
и закон аддитивности массы.

28. Движение тел с переменной массой

Рассмотрим системы, массы которых изменяются, например
ракета.
Наша задача: найти уравнение движения такого тела. Решение
этого вопроса покажем на примере ракеты.
Принцип действия ракеты состоит в следующем.
Ракета с большой скоростью выбрасывает вещество (продукты
сгорания), воздействуя на него с большой силой.
Выбрасываемое вещество с такой же, но противоположно
направленной силой в свою очередь действует на ракету и
сообщает ей ускорение в противоположном направлении.

29.

Движение тел с переменной массой на примере
ракеты.
Реактивное движение основано на принципе отдачи. В ракете
при сгорании топлива газы, нагретые до высокой температуры,
выбрасываются из сопла с большой скоростью.
Пусть в момент времени t масса ракеты m, а ее скорость . Спустя
время dt ее масса уменьшилась на dm и стала равной m – dm, а
скорость стала равной d . Изменение импульса системы за время
dt равно:
dP m dm d dm u m
где u скорость истечения газов относительно ракеты.

30.

dP md udm
Т.к. на ракету действуют внешние силы F (сила тяжести, сила
сопротивления воздуха), то согласно формуле
dp
, получим
F
dt
Fdt md udm
или
d dm
m
F u
dt
dt

31.

dm
Величина - u
FP - называется реактивной силой.
dt
Это сила, с которой действуют на ракету вылетающие
газы.
ma F FP
- уравнение движения тела с переменной массой
(уравнение Мещерского)

32.

Полученной формулой можно воспользоваться для
расчета зависимости скорости ракеты от массы
сожженного топлива. Будем считать, что внешние
силы равны 0, т.е. движение происходит только под
действием реактивной силы:
d
dm
m
u
dt
dt
откуда
dm
u
u ln m C
m
Значение постоянной интегрирования С определим
из начальных условий.

33.

Пусть в начальный момент времени скорость ракеты
равна 0, а масса равна m0. Отсюда С u ln(m0 ) .
Следовательно,
m
u ln 0 m
Это выражение называется формулой Циолковского.
Она показывает, что при данной скорости истечения
газов скорость ракеты определяется только
отношением начальной массы m0 ракеты к
оставшейся массе m.

34.

Вот процентное соотношение топлива от общей массы ракеты,
необходимое для попадания ракеты на орбиту Земли.
Вид топлива
Масса топлива от массы
ракеты
Твердое ракетное
топливо
96%
Керосин-кислород
94%
Самовоспламеняющеес
я топливо
93%
Метан-кислород
90%
Водород-кислород
83%
Полученные цифры не учитывают разнообразные потери сопротивления
атмосферы, неполного сгорания и других отрицательных факторов,
поэтому реальное отношение чуть ближе к 100%.

35. Закон сохранения механической энергии

• Рассмотрим систему, состоящую из N частиц.
• Силы взаимодействия между частицами
( F внутр. )
–
консервативные. Под действием этих сил тела системы
перемещаются, меняется их скорость и положение, т.е.
меняются кинетическая и потенциальная энергии
системы.
• Кроме внутренних сил на частицы действуют внешние
консервативные и неконсервативные силы, компенсируя
друг друга. Т. е. рассматриваемая система частиц или тел
замкнута.
• Механическая система называется замкнутой (или
изолированной), если на неё не действуют внешние
силы, т.е. она не взаимодействует с внешними телами.

36.

Запишем второй закон Ньютона для каждого тела.
Под действием сил тела системы совершают перемещения
d r1 , d r2 ......d rn
Умножим каждое уравнение на соответствующее перемещение.
Учитывая, что ,
получим:

37.

38.

Есть приращение кинетической энергии системы.
Второй член –
- есть
элементарная работа, совершаемая телами системы

39.

−
откуда
d E k E П 0,
E k E П const
Выражение представляет собой закон сохранения
механической энергии: полная механическая энергия
замкнутой системы, в которой действуют только
консервативные силы, сохраняется, т.е. не изменяется
со временем.
Может происходить лишь превращение кинетической
энергии в потенциальную и обратно, причем
приращение одной из них в точности равно убыли
другой.

40.

Если в замкнутой системе действуют неконсервативные
силы, то полная механическая энергия системы не сохраняется –
частично она переходит в другие виды энергии –
неконсервативные.
Система, в которой механическая энергия переходит в другие
виды энергии, называется диссипативной, а сам процесс
перехода называется диссипацией энергии.
В диссипативной, изолированной от внешнего воздействия
системе остаётся постоянной сумма всех видов энергии
(механической, тепловой и т.д.).
Здесь действует общий (полный) закон сохранения энергии.
Этот процесс хорошо демонстрирует маятник Максвелла.
Роль консервативной внешней силы здесь играет гравитационное
поле. Маятник прекращает свое движение из-за наличия
внутренних неконсервативных сил (сил трения, сопротивления
воздуха).

41. Применение законов сохранения

Удар – любое кратковременное взаимодействие тел,
результатом которого является значительное изменение скорости
их движения.
Так как два сталкивающихся тела, на которые не действуют
силы со стороны других тел, представляют собой замкнутую
систему, то к ним применим закон сохранения импульса, а во
многих случаях – и закон сохранения энергии.
Различают два вида ударов:
абсолютно неупругий удар
абсолютно упругий удар

42.

При абсолютно неупругом ударе закон сохранения
механической энергии не работает.
Применим закон сохранения механической энергии для
расчета скорости тел при абсолютно упругом ударе – это
такой удар, при котором не происходит превращения
механической энергии в другие виды энергии.
Абсолютно упругий удар бывает двух типов
нецентральный удар
центральный удар

43.

Пример 1. Абсолютно-упругий центральный удар
1
2
Два шара m1 и m2 и скоростями
(поэтому, хотя
скорости и направлены в одну сторону все равно будет удар).
Систему можно считать замкнутой. Кроме того, при
абсолютно упругом ударе она консервативна.
Обозначим ' и ' – скорости шаров после их столкновения.
В данном случае можно воспользоваться законом
сохранения механической энергии и законом сохранения
импульса (в проекциях на ось x):
1
2
m1 12 m2 22 m1 '12 m2 '22
2
2
2
2
m m m ' m ' .
1 1
2 2
1 1
2
2
По ЗСЭ
По ЗСИ

44.

m1 ( 12 '12 ) m2 ( '22 22 )
m1 ( 1 '1 ) m2 ( '2 2 ).
1 '1 '2 2
Получим в итоге:
2m2 2 (m1 m2 ) 1
'1
;
m1 m2
2m1 1 (m2 m1 ) 2
'2
m1 m2
Таким образом, скорости шаров после абсолютно упругого
удара не могут быть одинаковыми по величине и по
направлению.

45. Рассмотрим частные случаи: 1. Соударения одинаковых шаров:

m1 m 2
Выражения:
2m2 2 (m1 m2 ) 1
'1
;
m1 m2
2m1 1 (m2 m1 ) 2
'2
m1 m2
имеют вид
т.е. шары равной массы обмениваются скоростями

46. 2. Один шар до удара покоится:

Скорости шаров после соударения имеют вид:
И тогда поведение шаров зависит от соотношения масс

47.

б) m1 < m2. После удара направление движения первого шара
изменится – шар отскакивает обратно. Второй шар движется в
ту сторону, в которую двигался первый шар до удара.

48. в) m1 = m2. После удара остановится первый шар, а второй будет двигаться с той же скоростью и в том же направлении, в котором

двигался первый шар до удара
Таким образом, при абсолютно упругом ударе общая
кинетическая энергия тел сохраняется, но распределяется
между ними в зависимости от их масс и скоростей.

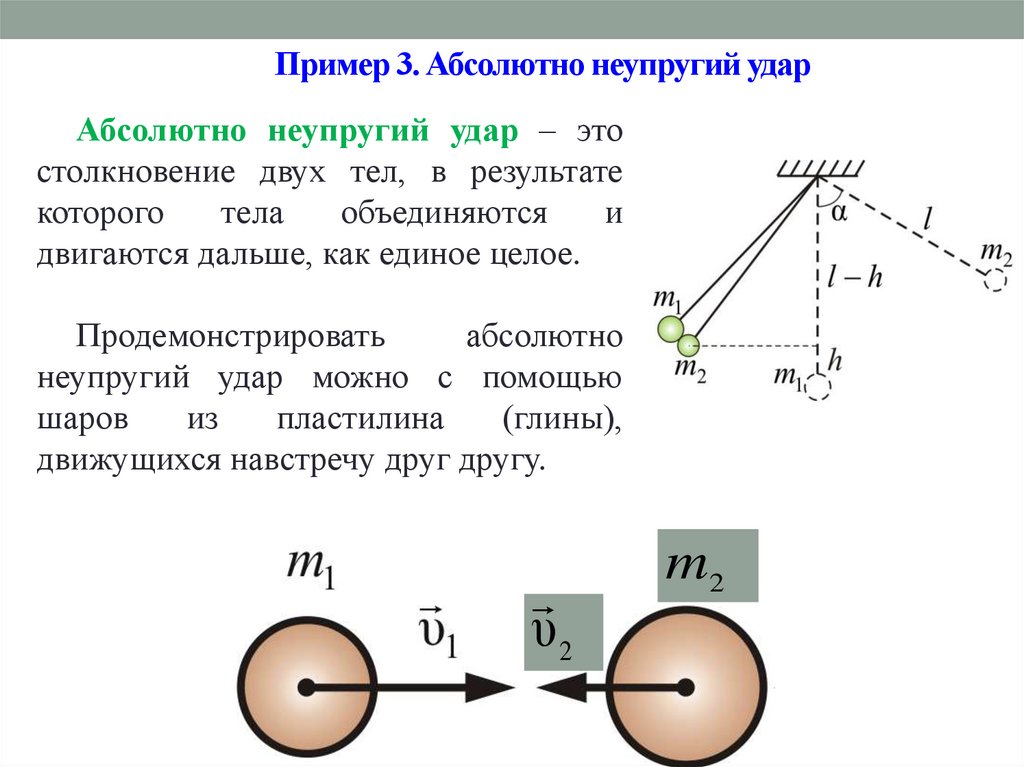
49. Пример 3. Абсолютно неупругий удар

Абсолютно неупругий удар – это
столкновение двух тел, в результате
которого
тела
объединяются
и
двигаются дальше, как единое целое.
Продемонстрировать
абсолютно
неупругий удар можно с помощью
шаров
из
пластилина
(глины),
движущихся навстречу друг другу.
υ2
m2

50.

Если массы шаров m1 и m2, их скорости до удара υ1 и υ2 то
используя закон сохранения импульса, можно записать
m1 1 m2 2 (m1 m2 )
– скорость движения шаров после неупругого удара:
m1 1 m2 2
.
m1 m2
Итак, скорость слипшихся
m1 1 m2 2
.
шаров после неупругого удара
m1 m2
Если шары двигались навстречу друг другу, то они вместе
будут продолжать двигаться в ту сторону, в которую двигался
шар, обладающий большим импульсом. В частном случае, если
массы и скорости шаров равны, то
1 2
2
0.
Выясним, как меняется кинетическая энергия шаров при
центральном абсолютно неупругом ударе.

51.

Так как в процессе соударения шаров между ними действуют
силы, зависящие не от самих деформаций, а от их скоростей, то
мы имеем дело с силами, подобными силам трения, поэтому
закон сохранения механической энергии не должен
соблюдаться.
Вследствие деформации происходит «потеря» кинетической
энергии, перешедшей в тепловую или другие формы энергии
(диссипация энергии). Эту «потерю» можно определить по
разности кинетических энергий до и после удара:
m1 12 m2 22 (m1 m2 ) 2
K
2
2
.
2
m1m2
2
K
1 2 .
2( m1 m2 )
Если ударяемое тело было первоначально неподвижно 2 0
то
m
m
m 2
Отсюда, получаем
1 1
m1 m2
, K
2
1 1
m1 m2
2
.

52.

Когда m2 >> m1 (масса неподвижного тела очень большая), то
υ << υ1 и почти вся кинетическая энергия при ударе переходит в
другие формы энергии. Поэтому, например, для получения
значительной деформации наковальня должна быть массивнее
молотка.
Когда m2 ≈ m1 тогда υ ≈ υ1 и практически вся энергия
затрачивается на возможно большее перемещение, а не на
остаточную деформацию (например, молоток – гвоздь).

53. Удар с частичной потерей энергии

• Промежуток
времени, в течение
которого длится удар, обычно очень мал
(на
практике
~10-4..10-5
с),
а
развивающиеся на площадках контакта
соударяющихся тел силы (ударные или
мгновенные) очень велики.
• За время удара они изменяются в
широких
пределах
и
достигают
значений,
при
которых
средние
величины давления (напряжений) на
площадках контакта имеют порядок 104
и даже 105 атм.
• Ввиду
малости
времени
удара,
импульсами всех неударных сил, таких,
например, как сила тяжести, а также
перемещениями точек тела за время
удара пренебрегают.