Similar presentations:
Закон сохранения механической энергии
1. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
2.
Лекцию читаетКандидат физико-математических наук,
доцент
Кузьмин Юрий Ильич
3.
Электронные адресаwww.nwpi.ru
physics@nwpi.ru
4.
Работа силы
Кинетическая энергия
Потенциальная энергия
Закон сохранения
механической энергии
5.
• Состояние механической системыхарактеризуется координатами и
импульсами (скоростями) входящих в неё
тел.
• Процесс изменения состояния системы
тел происходит под действием сил.
Количественно этот процесс
характеризуется понятием работа силы.
6.
• 1. Работа постоянной силыопределяется как
скалярное
произведение F на r
A F r
• A F r cos ;
• F cos Fr – проекция вектора
силы на направление перемещения .
7.
• 2. Работа переменной силы ( Fr const ).Вводится понятие элементарной работы
(dA) на малом отрезке dr , когда силу
можно считать постоянной, а движение
точки – прямолинейным.
dA Fdr FS dS
(2)
• где dS dr – элементарный
путь, FS –
проекция вектора F на перемещение.
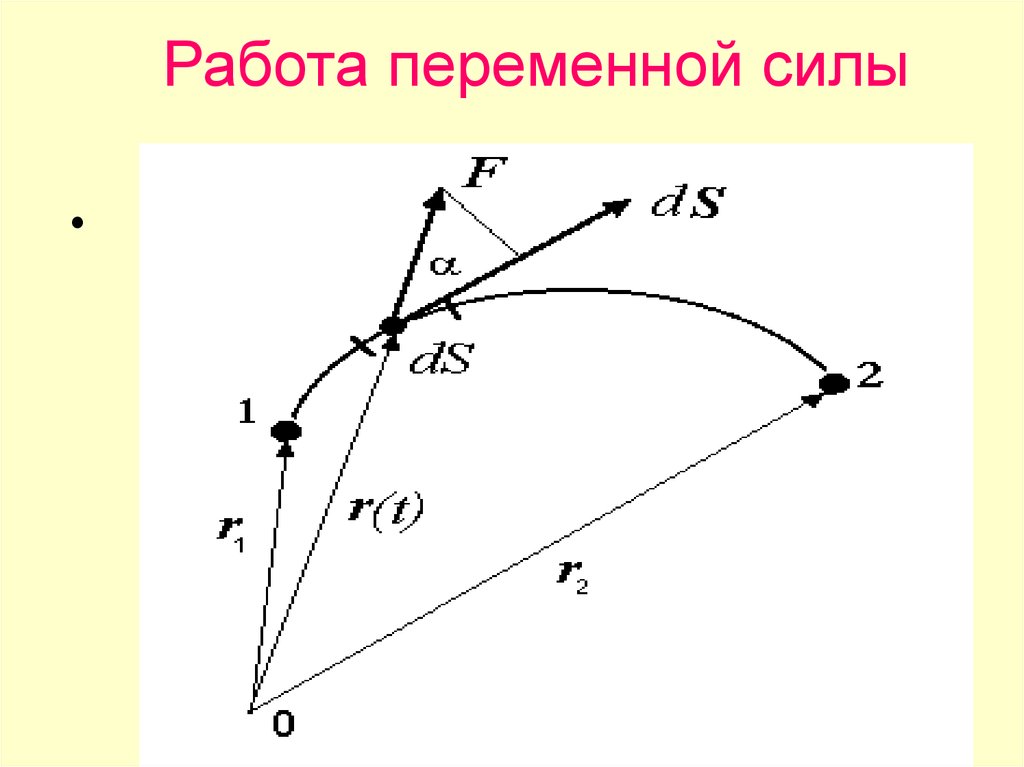
8. Работа переменной силы
9.
• Весь участок траектории от точки 1до точки 2 разбивается на
множество малых отрезков dr,
полная работа на всем пути равна
сумме элементарных работ, т.е.
2
А FS dS
1
10. Кинетическая и потенциальная энергия
• В механике рассматриваются два видаэнергии: кинетическая (Wk) и потенциаль –
ная (Wп), а полная механическая энергия
равна их сумме:
W Wk Wп
энергия тела (или механической системы) –
это энергия механического движения, она
зависит от массы и скорости тела.
11.
• Получим количественноевыражение для
Wk. Сила F , действуя на покоящееся тело,
вызывает его движение, совершая работу.
Энергия движущегося тела возрастает на
величину совершенной работы, т.е.
dA dWk
dv
• Используем второй закон Ньютона F m
dt
и, умножая F на перемещение dr , получим
выражение для работы постоянной силы:
(2)
dv
Fdr m dr dA
dt
12.
dr
• Так как v
, то элементарная работа
dt
• dA mvdv mvdv dWk ,(3)
откуда
v
2
mv
Wk mvdv
(4)
2
0
v
• т.е. общее выражение для Wk тела, движущегося
со скоростью v ,имеет вид:
2
mv
Wk
2
(5)
13.
• 2. Потенциальная энергия – этоэнергия взаимодействия, Wп зависит
от взаимного расположения тел и
характера действующих между
телами сил.
• В механике рассматриваются 2 вида
сил, действующих между телами:
консервативные и диссипативные.
14.
• Силы, работа которых при перемещениитела из одного положения в другое не
зависит от формы траектории, а зависит
только
от
начального
и
конечного
положений, называются консервативными.
Такими силами являются гравитационные
силы и силы упругости. В дальнейшем
покажем, что только в случае консерва –
тивных сил, действующих в замкнутой
системе, выполняется закон сохранения
механической энергии.
15.
• В качестве примера вычислимпотенциальную энергию
упругодеформированного тела (пружины).
Сила упругости Fупр kx , (6) Где k –
• жесткость (пружины).
• По третьему закону Ньютона
деформирующая сила равна по модулю силе
упругости и противоположно ей направлена
F Fупр kx .Элементарная работа dA,
совершаемая силой F при малой
деформации dx, равна
dA Fdx kxdx
16.
• а полная работаx
2
kx
A kxdx
2
0 потенциальной
идет на увеличение
энергии пружины.
• Таким образом
kx
Wп
2
(7)
2
• Существенно, что работа равна
изменению энергии
A W W2 W1
(8)
17. Закон сохранения механической энергии
• Формулировка: Полная механическаяэнергия замкнутой системы, в которой
действуют только консервативные силы,
сохраняется постоянной во времени, т.е.
(1)
W Wk Wп const
Проиллюстрируем действие этого закона
на примере свободного падения тел.
18.
• Известно, что тело, поднятое на высоту h• вблизи поверхности Земли, обладает
W mgh
• потенциальной энергией
п
Предоставленное самому себе, тело будет
падать, набирая скорость. При этом сила
тяжести совершает работу за счет убыли
потенциальной энергии.
• Элементарная работа dA на малом отрезке
dr:
(2)
dA -dWп
19.
• Одновременно эта работа идет наувеличение кинетической энергии тела,
т.е.
dA dWk
(3)
• Поскольку левые части выражений (2) и
(3) одинаковы, то одинаковы и правые:
(4)
- dWп dWk
• т.е. убыль потенциальной энергии
сопровождается ростом кинетической
энергии.
20.
• Следовательно,т.е.
d (Wk Wп ) 0
W Wk Wп const
• Выражение (6) – математическая запись закона
сохранения энергии. Существенно, что это не
только закон сохранения, но и превращения
одного вида энергии в другой.
• Закон сохранения энергии – фундаментальный
закон природы, он справедлив как для систем
макроскопических тел, так и для систем
микромира.
21.
• В системе, в которой действуют такженеконсервативные силы, например силы
трения, полная механическая энергия не
сохраняется. В этом случае выполняется
более общий закон сохранения энергии.
• Его формулировка: В изолированной
системе сохраняется постоянной
сумма всех видов энергии –
механических и немеханических.
22. Задача
• . В пружинном ружье пружинасжата на 10 см. При взводе её
сжали на 20 см. С какой
скоростью вылетит из ружья
стрела массой 30 г, если жесткость
пружины 144 Н/м.
23. Дано:
х1 0,1 мх 2 0,2 м
m 3 10
2
кг
Н
k 1,44 10
м
2
– ------------------------
v ?
24. Решение
• Закон сохранения энергии:kx
kx
mv
2
2
2
2
2
2
1
2
,
2
• .k
1,44 10
м
2
2
2
v ( x2 x1 )
(4 1) 10 144 12
2
m
3 10
с
25. Задача
• Ракета, масса которой вместе сзарядом равна 250 г, взлетает
вертикально вверх и достигает
высоты 150 м. Определить скорость
истечения газов из ракеты, считая,
что сгорание заряда происходит
мгновенно. Масса заряда равна 50 г.
26. Дано:
m1 0,250 кгm2 0,05 кг
h 150 м
• --------------------
v ?
27. Решение
• Закон сохранения импульса0 0 (m1 m2 ) v1 m2 v2
• где
v1 2 gh
(m1 m2 )
v2
2 gh 219 м/с
m2
28. Упругий и неупругий удары шаров
• Рассматривается прямой центральныйудар шаров.
• 1. Неупругий удар. После соударения оба
тела движутся вместе или покоятся.
Вследствие удара происходят потери
механической энергии (механическая
энергия частично переходит в тепловую
или энергию остаточных деформаций). В
случае такого удара выполняется только
закон сохранения импульса.
29.
• Силы взаимодействия между телами стольвелики, что систему можно считать
замкнутой.
• Запишем закон сохранения импульса для
шаров в проекции на ось Х (направление
движения):
m1v1 m2 v2 (m1 m2 )u (1)
• Откуда скорость шаров после удара
m1 v1 m2 v2
u
m1 m2
(2)
где знак “минус” соответствует движению
шаров навстречу друг другу.
30.
• Пример: два шара массой 1 кгкаждый двигались с
одинаковыми скоростями 5 м/с
навстречу друг другу. Определить
скорость шаров после неупругого
удара.
31.
• 2. Абсолютно упругий удар. После удараоба тела полностью восстанавливают
свою форму. При этом ударе выполняются
два закона сохранения: импульса и
механической энергии.
• Скорости шаров до удара обозначим v1 и
v2, а после удара u1 и u2.
• Запишем закон сохранения энергии:
2
2
2
2 (3)
m1v1 m2 v2 m1 u1 m2 u 2
2
2
2
2
32.
m1v1 m2 v2 m1u1 m2u2v1 (m1 m2 ) 2m2 v2
u1
m1 m2
2m1 v1 (m2 m1 ) v2
u2
m1 m2
33.
• Рассмотрим пример № 1.Два шара с кинетическими энергиями по
2,5 Дж каждый двигались навстречу друг
другу. Чему равна полная кинетическая
энергия шаров после упругого удара?
• Пример № 2.
При вертикальном падении шарика на
массивную плиту (удар абсолютно
упругий). Импульс, переданный плите,
равен:
1) mv ; 2) - mv ; 3) p 0 ; 4) p 2mv
• Укажите номер правильного ответа.





















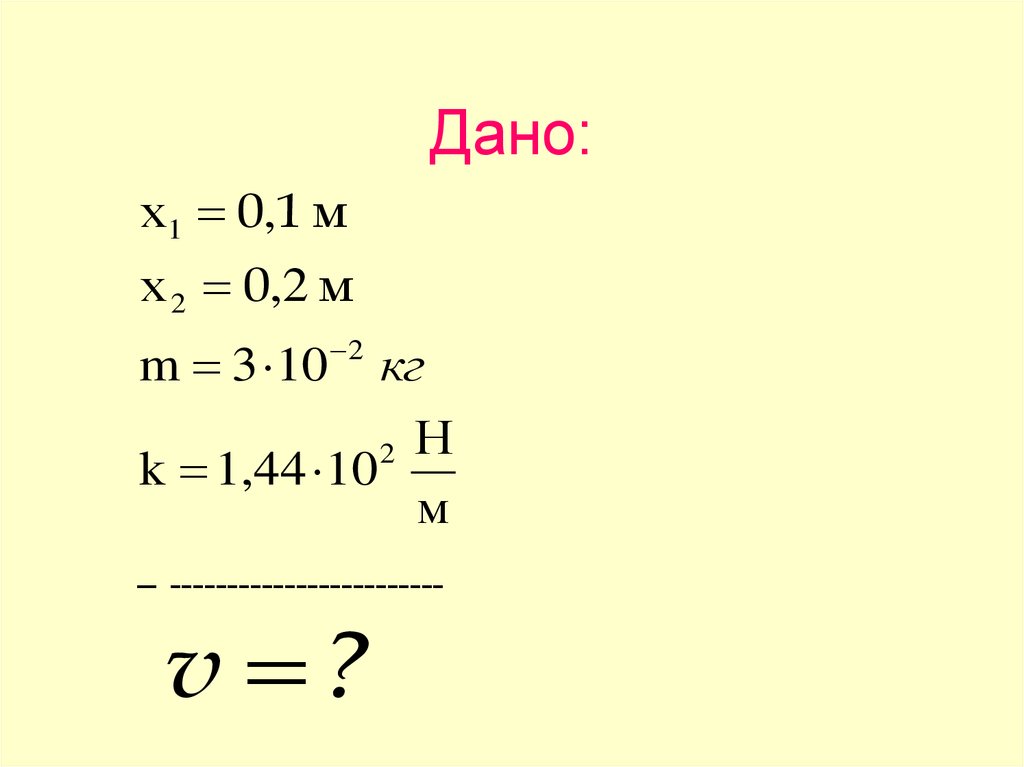








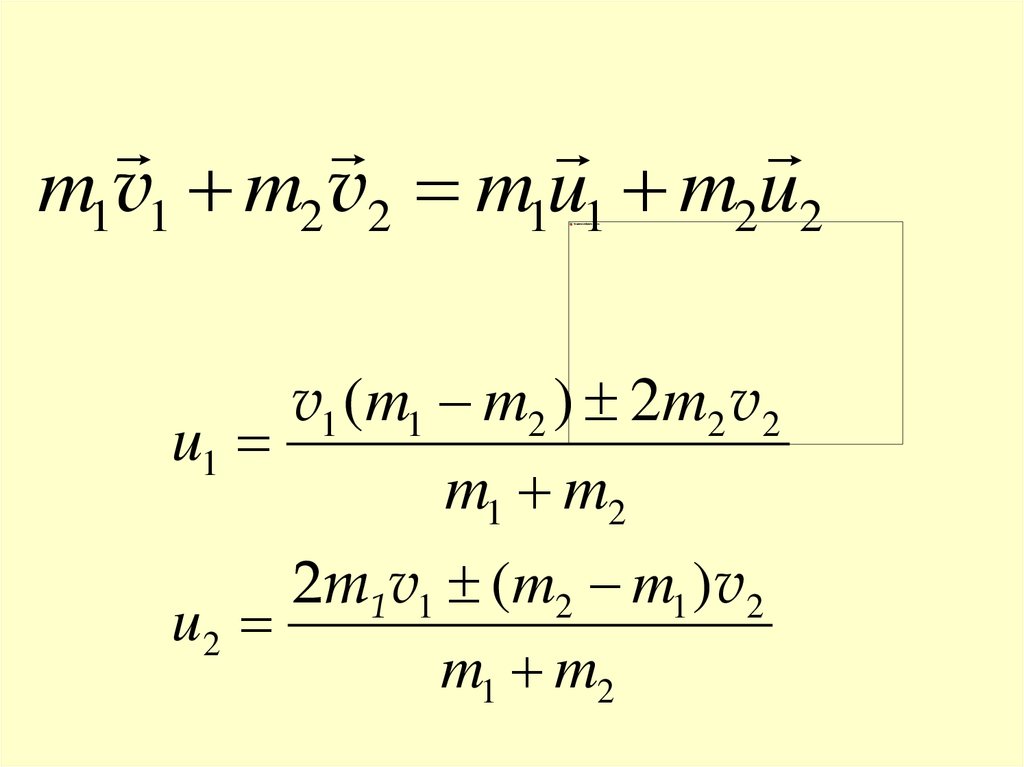

 physics
physics








