Similar presentations:
Закон сохранения энергии. Работа и кинетическая энергия
1.
Закон сохранения энергииРабота и кинетическая энергия
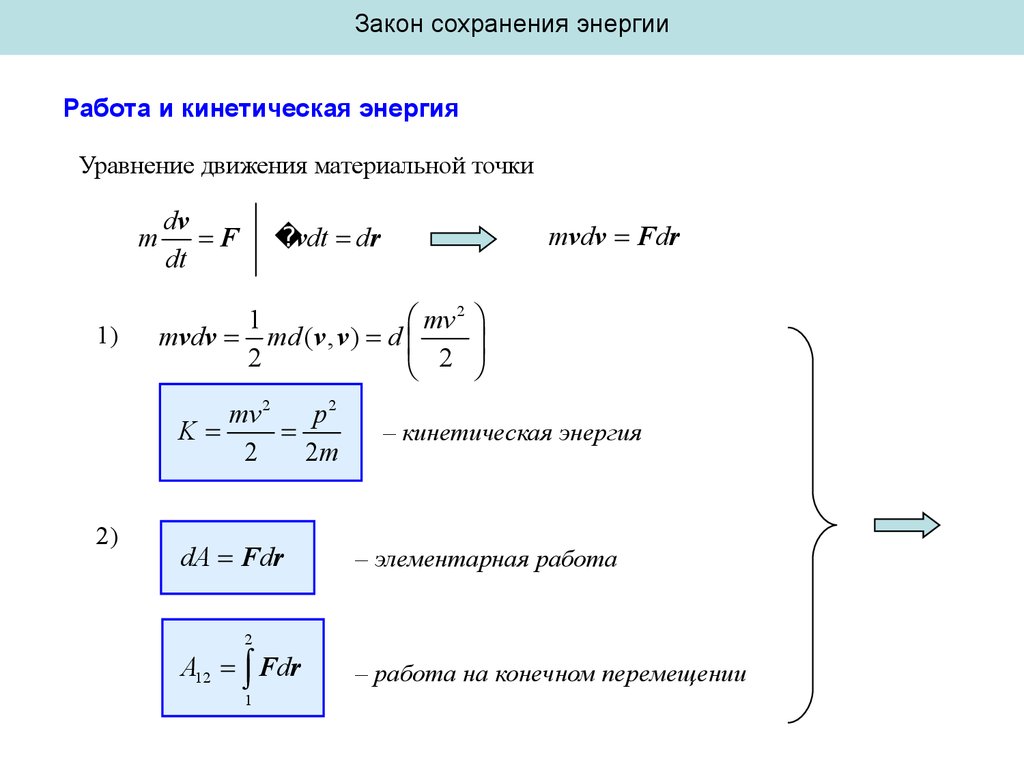
Уравнение движения материальной точки
m
1)
dv
F
dt
mv 2
1
mvdv md (v , v ) d
2
2
mv 2
p2
K
2
2m
2)
mvdv Fdr
vdt dr
dA Fdr
– кинетическая энергия
– элементарная работа
2
A12 Fdr
1
– работа на конечном перемещении
2.
Закон сохранения энергииРабота и кинетическая энергия
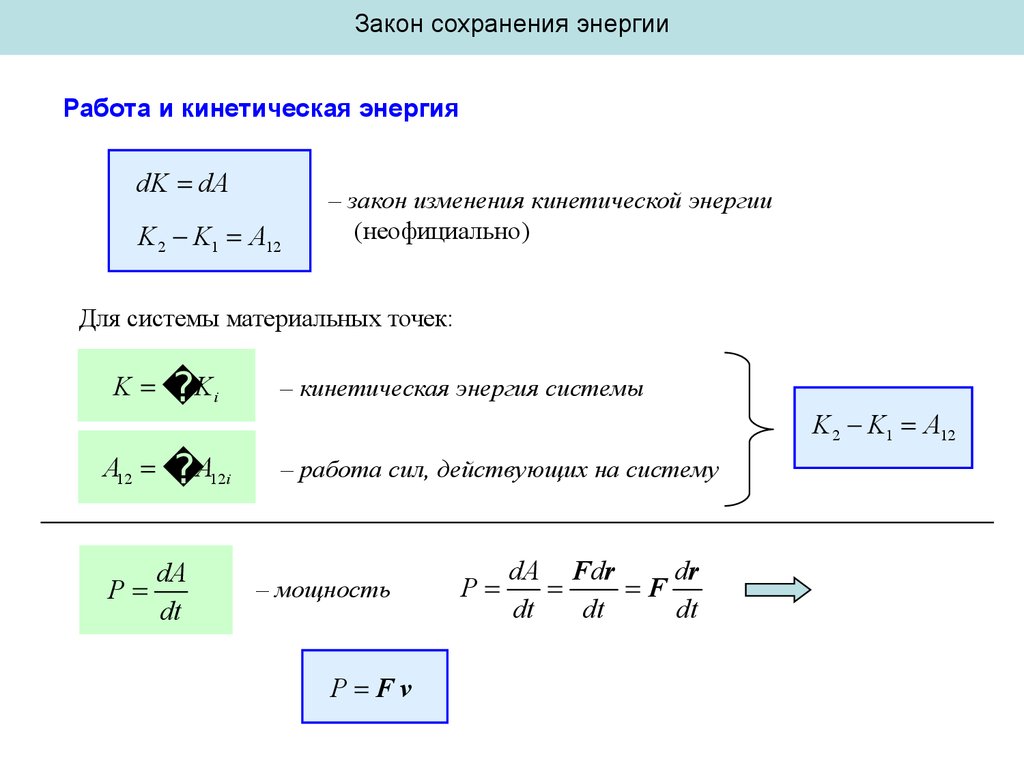
dK dA
K 2 K1 A12
– закон изменения кинетической энергии
(неофициально)
Для системы материальных точек:
K K i
A12 A12i
dA
P
dt
– кинетическая энергия системы
K 2 K1 A12
– работа сил, действующих на систему
– мощность
P Fv
P
dA Fdr
dr
F
dt
dt
dt
3.
Закон сохранения энергииКонсервативные и неконсервативные силы
консервативные
Силы
неконсервативные
диссипативные
гироскопические
Примеры: сила тяжести – консервативная сила
сила трения – неконсервативная сила
Определение:
Консервативные силы – это силы,
1) которые зависят только от координат материальных точек;
2) работа которых определяется только начальным и конечным
положениями системы и не зависит от пути.
4.
Закон сохранения энергииКонсервативные и неконсервативные силы
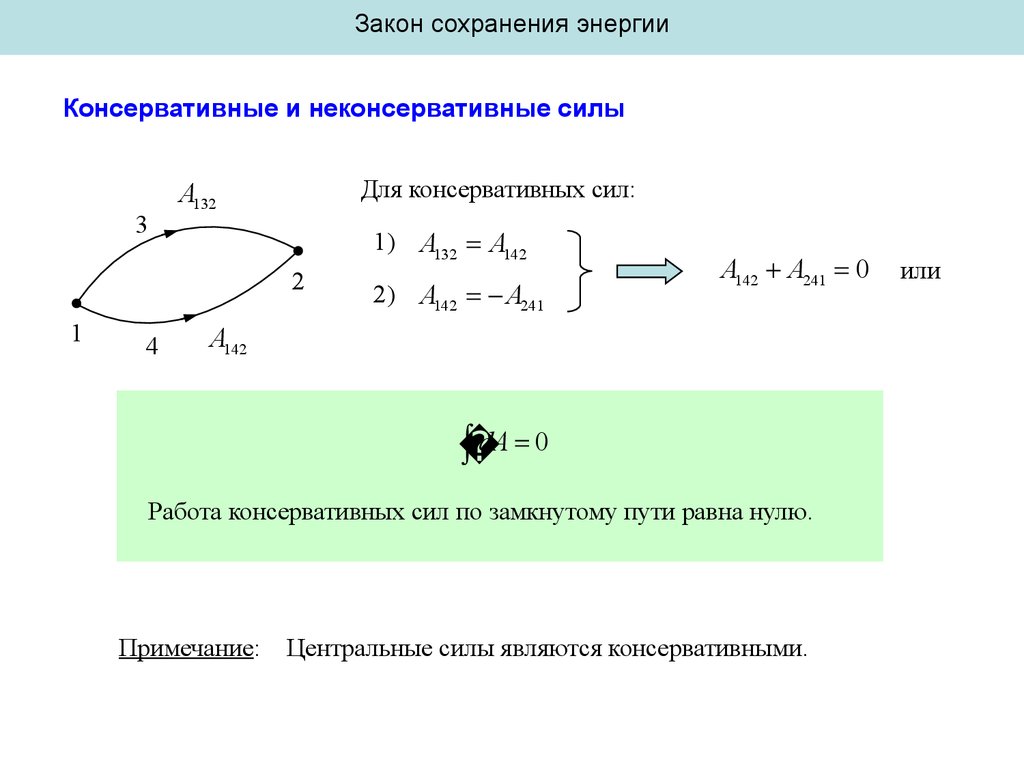
Для консервативных сил:
A132
3
1)
2
1
4
2)
A132 A142
A142 A241
A142 A241 0
A142
dA 0
Работа консервативных сил по замкнутому пути равна нулю.
Примечание:
Центральные силы являются консервативными.
или
5.
Закон сохранения энергииПотенциальная энергия
Консервативная система – это система, в которой действуют только
консервативные силы.
Для консервативной системы A12 не зависит от пути 1 → 2 и поэтому
можно определить функцию U:
U1 U 2 A12
Определение:
( dU dA)
U – потенциальная энергия
dK dA dU
dK dU 0
K U const
E K U
– закон сохранения механической энергии
(для консервативных систем)
– механическая энергия
6.
Закон сохранения энергииПотенциальная энергия силы тяжести
F mg
h
2
g
1
2
2
1
1
A12 mg dr mg dh mg (h2 h1 )
A12 (U 2 U1 )
U mgh C
=0
U mgh
Нормировка h = 0, U = 0
7.
Закон сохранения энергииПотенциальная энергия силы упругости
Fу kx
Fу
2
0
x
2
1
A12 Fdr k x dx k ( x22 x12 )
2
1
1
A12 (U 2 U1 )
=0
kx 2
U
C
2
kx 2
U
2
Нормировка x = 0, U = 0
8.
Закон сохранения энергииПотенциальная энергия гравитационного (кулоновского) поля
F
1
r
m
M – неподвижна (центр)
2
F
Mm r
r2 r
2
1 1
rdr
dr
A12 Mm 3 Mm 2 Mm
r2 r1
r
r
1
1
2
M
A12 (U 2 U1 )
=0
Mm
U
C
r
Mm
U
r
Нормировка r = , U = 0
U
1 q1q2
4 0 r
– для кулоновского
поля
9.
Закон сохранения энергииЗакон сохранения энергии
Закон изменения кинетической энергии:
dK dA dAк dAд
dAк – работа консервативных сил,
dAд – работа диссипативных сил
dAк dU
dE d ( K U ) dAд
E ( K U ) Aд
– закон изменения механической энергии
(неофициально)
1) В замкнутой системе dAд ≤ 0, т.е. E уменьшается;
2) Уменьшение E сопровождается нагревание тел.
10.
Закон сохранения энергииЗакон сохранения энергии
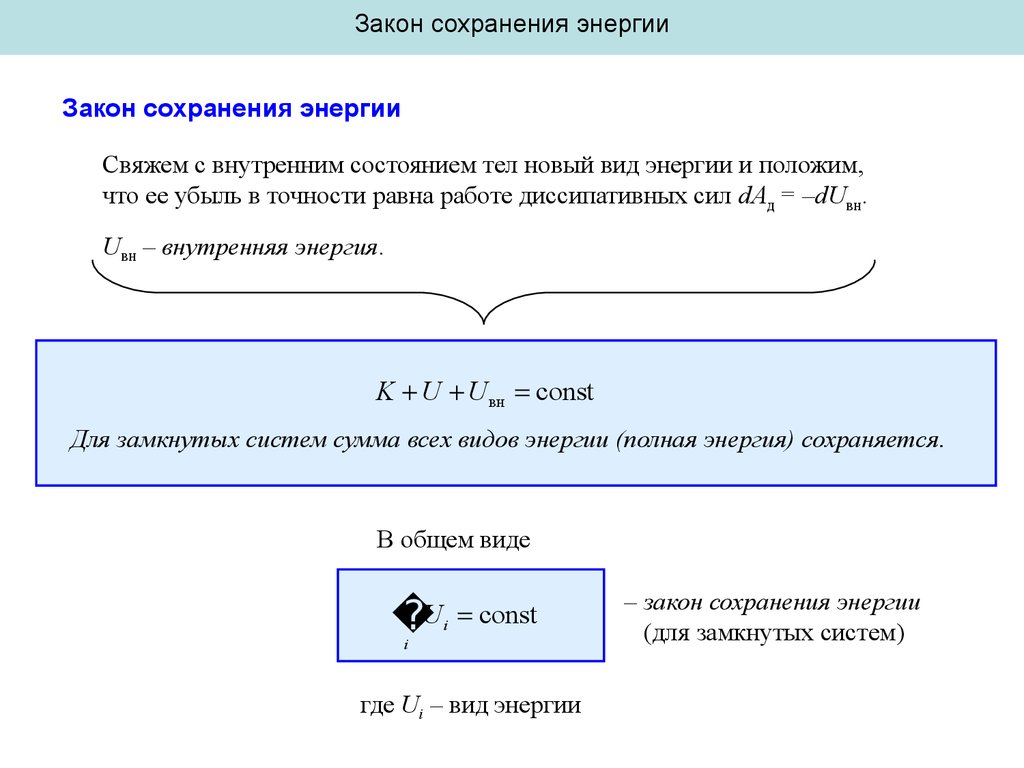
Свяжем с внутренним состоянием тел новый вид энергии и положим,
что ее убыль в точности равна работе диссипативных сил dAд = –dUвн.
Uвн – внутренняя энергия.
K U U вн const
Для замкнутых систем сумма всех видов энергии (полная энергия) сохраняется.
В общем виде
U
i
const
i
где Ui – вид энергии
– закон сохранения энергии
(для замкнутых систем)
11.
Закон сохранения энергииАбсолютно неупругий удар
Это столкновение тел, в результате которого они соединяются вместе и
движутся дальше как одно тело.
m1, v1
m2, v2
m, v
…
x
По закону сохранения импульса
v
m1v1 m2 v2 (m1 m2 ) v
m1v1 m2 v2
m1 m2
12.
Закон сохранения энергииАбсолютно неупругий удар
K1
1
2
m1v12 1 2 m2 v22
K1 K 2 1 2 (v1 v2 ) 2
K 2 1 2 (m1 m2 ) v 2
m1 m2
m1 m2
– приведенная масса
Неупругое столкновение шаров сопровождается потерей кинетической
энергии – часть кинетической энергии переходит во внутреннюю
энергию соударяющихся тел.
K2
K1
Uвн
13.
Закон сохранения энергииАбсолютно упругий удар
Это столкновение тел, в результате которого их внутренние энергии
(внутреннее состояние) не изменяются. Следовательно, при таком
столкновении сохраняется кинетическая энергия системы.
m1, v1
m2, v2
…
m1, v1'
m2 , v 2 '
x
По закону сохранения импульса и энергии
m1v1 m2 v2 m1v1 m2 v2
m1v1 2 m2v2 2 m1v12 m2v22
2
2
2
2
Система имеет два решения относительно неизвестных v1' и v2‘:
14.
Закон сохранения энергииАбсолютно упругий удар
1)
v1
v1 , v2 v2
2)
v1 v1 2
– столкновения еще не было
m1v1 m2 v2
m1 m2
v2 v2 2
m1v1 m2 v2
m1 m2
Случай, когда второй шар был неподвижен v2 = 0
v1
m1 m2
v1
m1 m2
v2
2m1
v1
m1 m2
а) m1 m2 v1
v1
б) m1 m2 v1
v1
c) m1 m2 v1
0, v2 v1
– обмен скоростями










 physics
physics








