Similar presentations:
Условия Гаусса-Маркова
1. Условия Гаусса-Маркова
Для того чтобы полученные по МНК оценкиобладали некоторым полезными статистическими
свойствами
необходимо
выполнение
ряда
предпосылок относительно оцениваемой модели,
называемыми условиями Гаусса-Маркова.
2. Условия Гаусса-Маркова
yi axi b i i 1, n1. M i 0
i 1, n
На самом деле это требование несущественно,
если в модель включена константа
3. Условия Гаусса-Маркова
yi axi b i2
i 1, n
D
2.
i
i 1, n
условие гомоскедастичности
(постоянства дисперсии)
4.
Условия Гаусса-МарковаИллюстрация гомоскедастичности
Регрессия
y = 3,4931+1,9952*x
400
350
300
250
y
200
150
100
50
0
-50
-20
0
20
40
60
80
100
x
120
140
160
180
200
5.
Условия Гаусса-МарковаИллюстрация гетероскедастичности
Регрессия
y = -5,741+2,1624*x
1400
1200
1000
800
y
600
400
200
0
-200
-400
-600
-20
0
20
40
60
80
100
x
120
140
160
180
200
6. Условия Гаусса-Маркова
yi axi b ii 1, n
3. cov i , j 0 i j
автокорреляция отсутствует
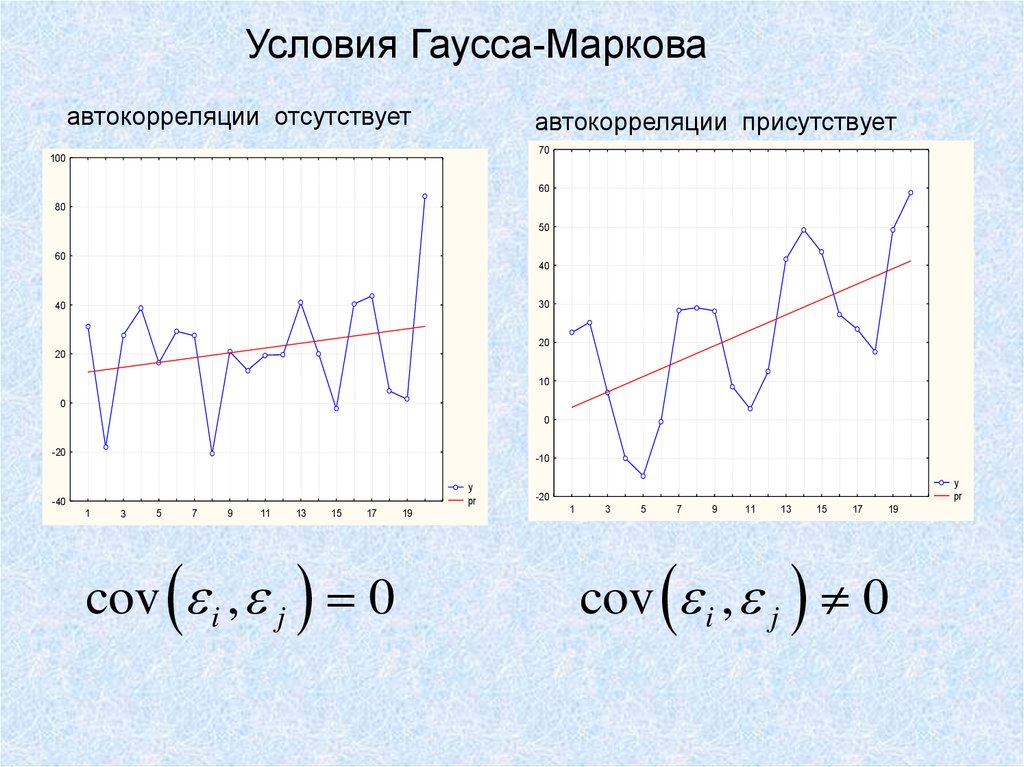
7.
Условия Гаусса-Марковаавтокорреляции отсутствует
автокорреляции присутствует
70
100
60
80
50
60
40
30
40
20
20
10
0
0
-20
-10
y
pr
-40
1
3
5
7
9
11
13
15
17
cov i , j 0
19
y
pr
-20
1
3
5
7
9
11
13
15
17
19
cov i , j 0
8.
Условия Гаусса-МарковаЕсли выполнены все 3 условия, то модель yi
i 1, n
axi b i ,
называется классической линейной моделью
парной регрессии
9.
Условия Гаусса-МарковаЕсли к 3-м условиям добавляют четвертое
4) Нормальность ошибок: i
То модель
N 0, 2
yi axi b i ,
i 1, n
называется
классической нормальной линейной моделью
парной регрессии
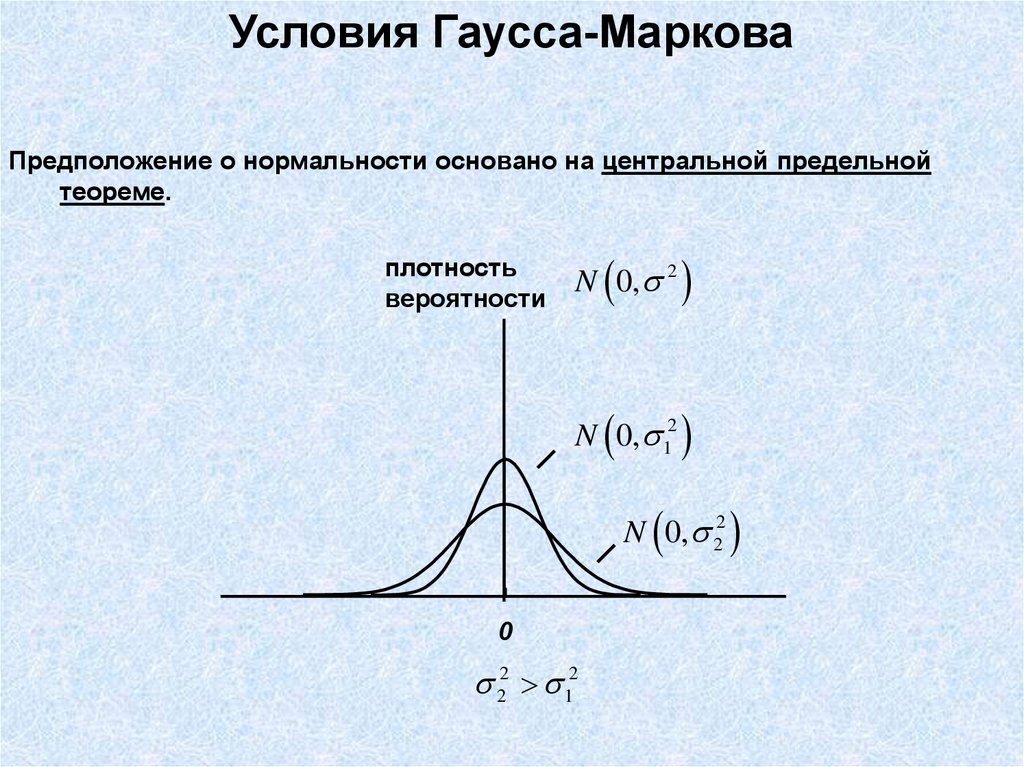
10.
Условия Гаусса-МарковаПредположение о нормальности основано на центральной предельной
теореме.
плотность
вероятности
N 0, 2
N 0, 12
N 0, 22
0
22 12
11. ТЕОРЕМА ГАУССА-МАРКОВА
В КЛАССИЧЕСКОЙ ЛИНЕЙНОЙ МОДЕЛИ ПАРНОЙ РЕГРЕССИИ(выполнены 3 условия Гаусса-Маркова) ОЦЕНКИ НАИМЕНЬШИХ
КВАДРАТОВ
cov( x, y )
a
2
sx
b y a x
ЯВЛЯЮТСЯ НАИЛУЧШИМИ (имеют наибольшую точность).
Если модель является нормальной (выполнены 4 условий ГауссаМаркова), то ОНК имеют нормальное распределение
Нормальность позволяет проверять гипотезы и строить доверительные
интервалы для прогноза.
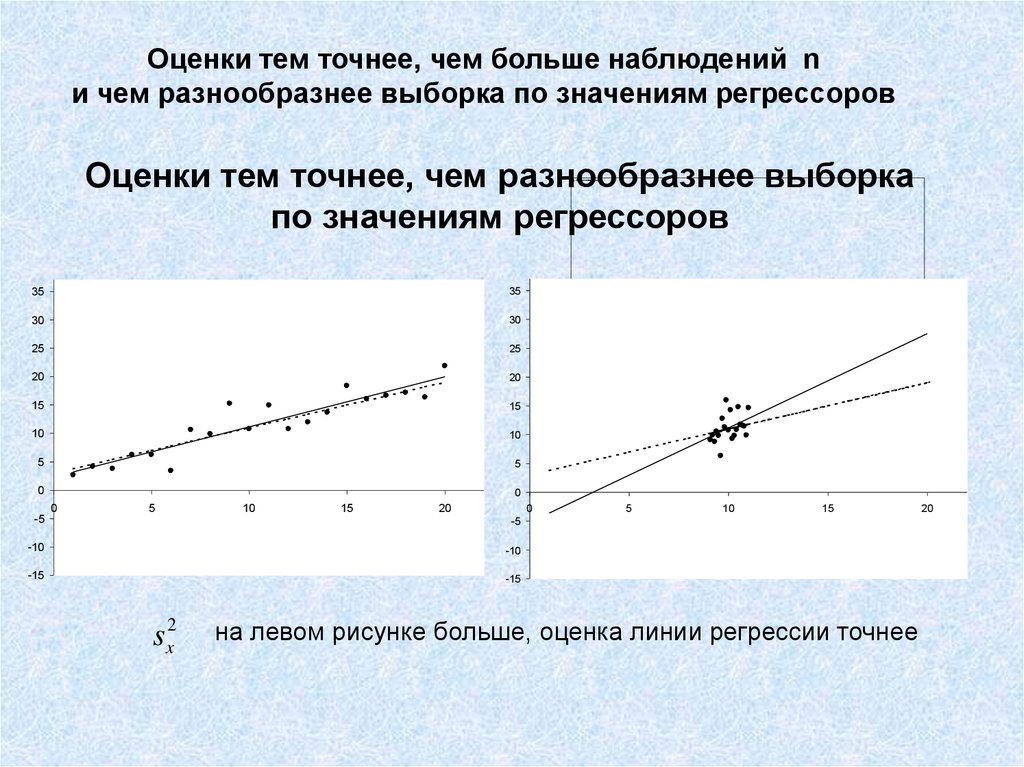
12.
Оценки тем точнее, чем больше наблюдений nи чем разнообразнее выборка по значениям регрессоров
Оценки тем точнее, чем разнообразнее выборка
по значениям регрессоров
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
0
5
10
15
20
0
-5
-5
-10
-10
-15
-15
sx2
5
10
15
на левом рисунке больше, оценка линии регрессии точнее
20









 mathematics
mathematics








