Similar presentations:
Векторы. Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторов
1. Векторы Разложение вектора по направлениям Координаты вектора Скалярное произведение векторов
2.
Вектор (направленный отрезок) отрезок, для которого указано, какая из его граничных точек считаетсяначалом, а какая – концом.
Обозначение:
или
Конец вектора
В
Длиной или модулем вектора
называется длина отрезка АВ:
АВ = АВ
А
Начало
вектора
a
3.
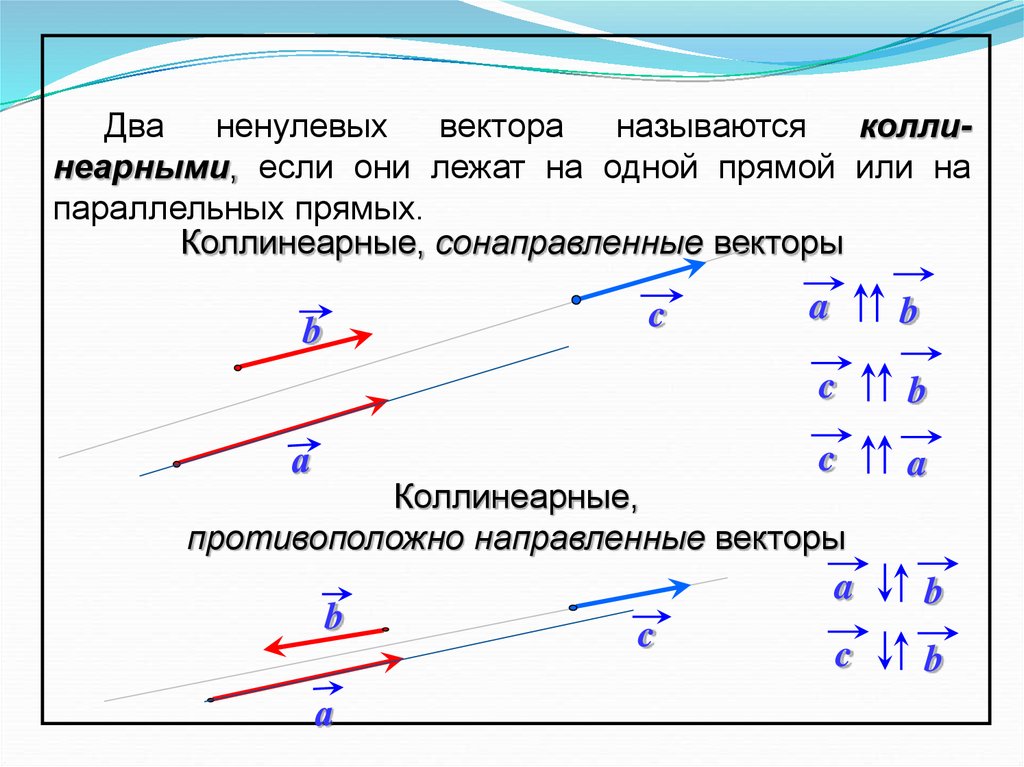
Дваненулевых вектора
называются
коллинеарными, если они лежат на одной прямой или на
параллельных прямых.
Коллинеарные, сонаправленные векторы
c
b
a
b
c
b
c
a
Коллинеарные,
противоположно направленные векторы
b
c
a
b
c
b
4.
Векторыназываются
равными,
сонаправлены и их длины равны.
В
А
С
a
a
если
=
они
b
b
D
Векторы называются противоположными, если они
противонаправлены и их длины равны.
В
А
С
D
a b
a= b
5.
РассмотримПДСК. Единичным вектором коор-
динатной оси будем называть вектор, направление
которого совпадает с направлением этой оси и длина
которого равна 1.
i – единичный вектор оси абсцисс,
j – единичный вектор ос и ординат,
k – единичный вектор оси аппликат.
z
k
O
j
x
i
y
6.
Любой вектор можно разложитьвекторам, т.е. представить в виде:
по
координатным
Нулевой вектор также можно представить в таком виде:
Координаты равных векторов соответственно равны:
Сумма (разность) векторов:
Произведение вектора на число:
7.
Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-векторомданной точки. Координаты любой точки равны соответствующим координатам её радиус-вектора.
8.
Координаты середины отрезкаДлина вектора по его координатам:
9.
Даны векторы:Найти вектор, равный:
Найдите значения m и n, при которых векторы
коллинеарны.
10.
АУгол между векторами
а
О
Если
Если
Если
α
В
b
и
,то
и
, то.
, то
11.
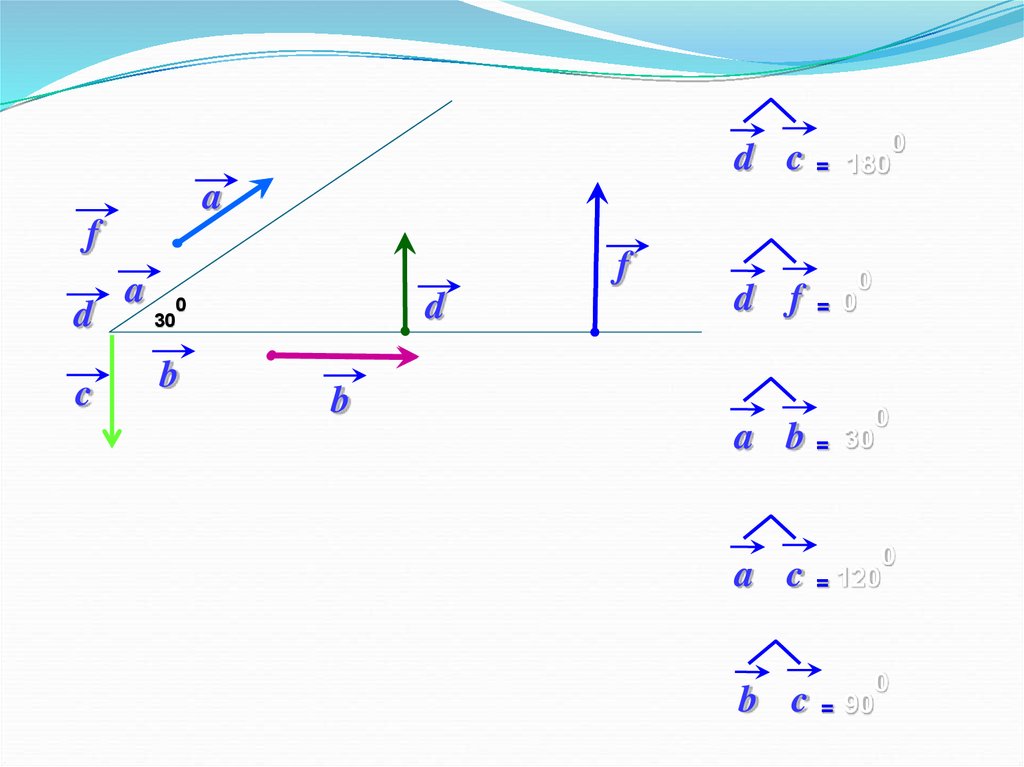
d c= 180
0
a
f
d
c
f
a
30
d
0
b
d f
= 0
0
b
a b
a c
b c
= 30
0
= 120
= 90
0
0
12.
Скалярным произведением двух векторов называетсяпроизведение их длин на косинус угла между ними.
a
b
=
a
b cos( a b)
Скалярное произведение векторов – число (скаляр).
Если векторы перпендикулярны, то скалярное произведение
этих векторов равно нулю.
0
a b = 90
b
a
13.
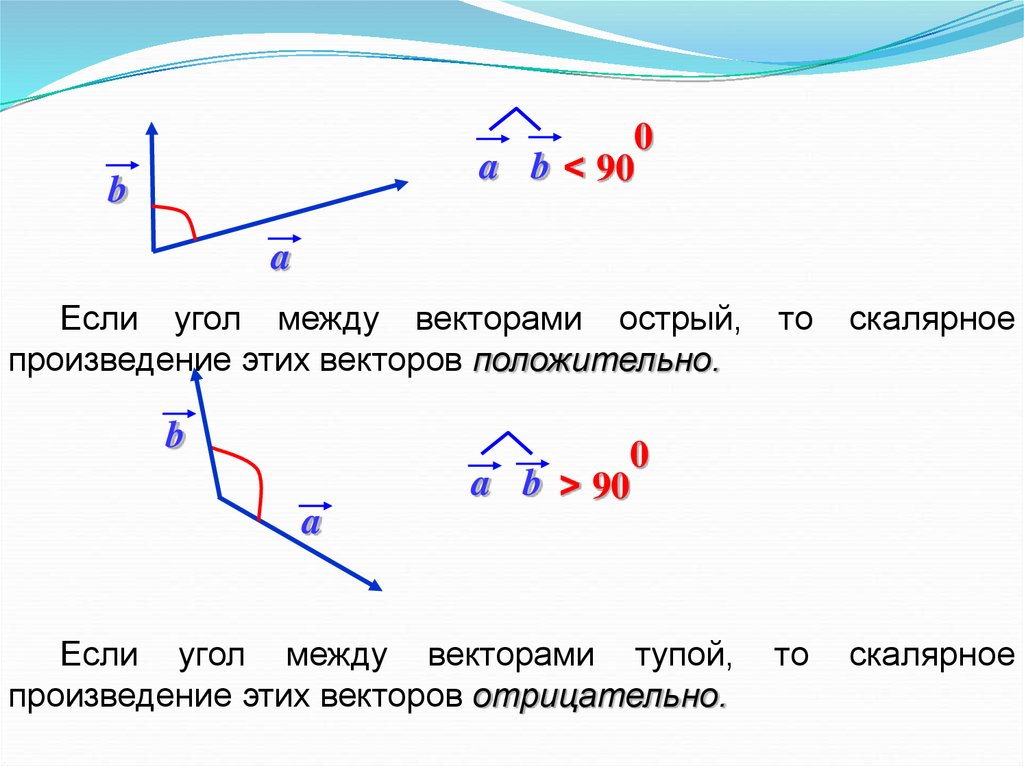
a b < 90b
0
a
Если угол между векторами острый,
произведение этих векторов положительно.
b
a b > 90
то
скалярное
то
скалярное
0
a
Если угол между векторами тупой,
произведение этих векторов отрицательно.
14.
a b=
a
b сos (a b )
Пусть векторы заданы своими координатами a ( x1; y1; z1 )
и b ( x2; y2; z2 ). Тогда скалярное произведение этих векторов
равно
2
a · b = x1x2 + y1y2 + z1z2
2
a = |a|
cos
x1 x2 y1 y2 z1 z 2
x12 y12 z12 x22 y22 z 22
cos
a b
| a | | b |











 mathematics
mathematics








