Similar presentations:
Координаты векторов. Действия над векторами в координатной форме. Скалярное произведение векторов. Угол между
1. Занятие 54 Координаты векторов. Действия над векторами в координатной форме. Скалярное произведение векторов. Угол между
векторами.2.
Единичный вектор – вектор, длина которого равна 1.i – единичный вектор оси абсцисс, j – единичный вектор
оси ординат, k – единичный вектор оси аппликат.
z
k
j
O
i
x
y
3.
Любой вектор ā можно разложить покоординатным векторам, т.е. представить в
виде:
а хi y j z k
Нулевой вектор можно представить в виде:
0 0i 0 j 0k
Координаты равных векторов соответственно
равны, т.е., если
ā { x1; y1; z1} = b { x2; y2; z2}, то
x1 = x2, y1 = y2, z1 = z2.
4. Определите координаты векторов:
zА1
В1
ОА1= 1,5
ОА2= 2,5
ОА = 2
1
k
i
О
В
j
y
1
OВ1 0;2,5;1,5
OВ2 2;2,5;0
1
А
x
А2
В2
?
OВ 2;2,5;1,5
5. Разложите все векторы по координатным векторам
Проверяем:ОА1 0 i 0 j 1,5 k
ОА2 0 i 2,5 j 0 k
ОА 2 i 0 j 0 k
ОB1 0 i 2,5 j 1,5 k
ОB2 2 i 2,5 j 0 k
ОB 2 i 2,5 j 1,5 k
6. Правила действий над векторами с заданными координатами
1. Каждая координата суммы двух и более векторов равнасумме соответствующих координат этих векторов.
Дано:
а х1; у1; z1
b х2 ; у2 ; z2
Доказать:
с a b
с х1 х2 ; у1 у2 ; z1 z2
a b х1 i y1 j z1 k x2 i y2 j z2 k
x1 x2 i y1 y2 j z1 z2 k с
Следовательно с х х ; у у ; z z
1
2
1
2
1
2
7. Правила действий над векторами с заданными координатами
2. Каждая координата произведения вектора на числоравна произведению соответствующей координаты
на это число.
Дано: а х; у; z α – произв.число a с
Доказать: с х; у; z
3. Каждая координата разности двух векторов равна
число равна разности соответствующих координат
на этих векторов.
Дано: а х1 ; у1 ; z1 b х2 ; у2 ; z2 с a b
Доказать: с х1 х2 ; у1 у2 ; z1 z 2
8.
Связь между координатами векторови координатами точек
9.
Связь между координатами векторови координатами точек
Каждая координата вектора равна
разности соответствующих координат его конца и начала.
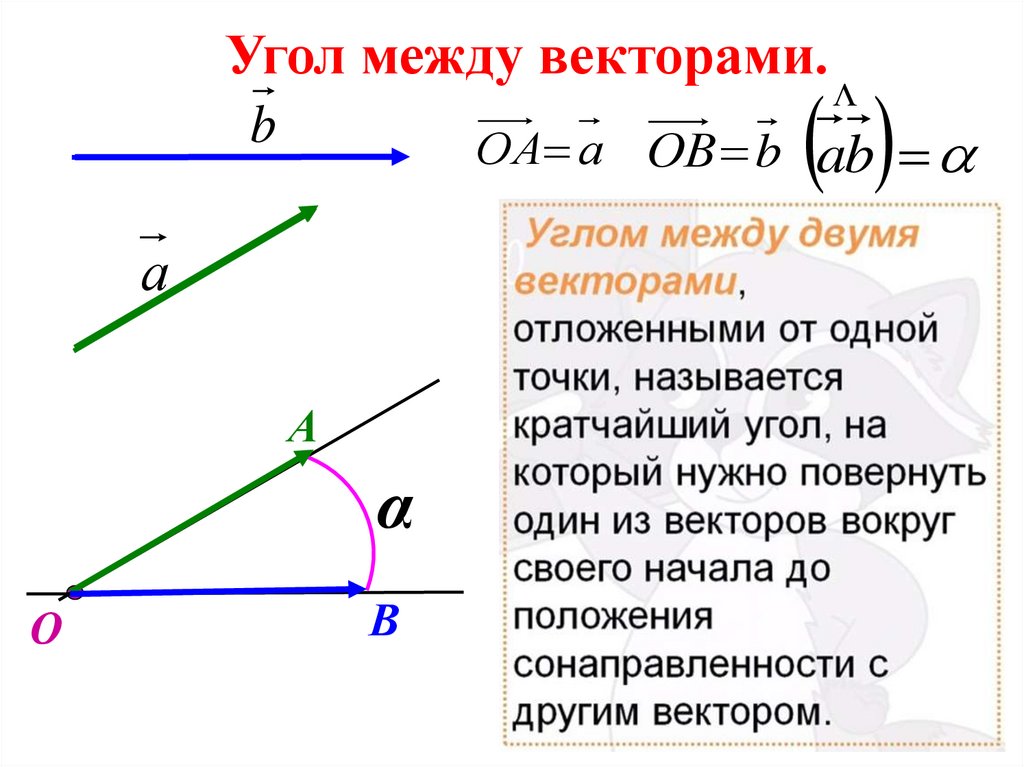
10.
Угол между векторами.b
ОА а ОВ b ab
а
А
α
О
В
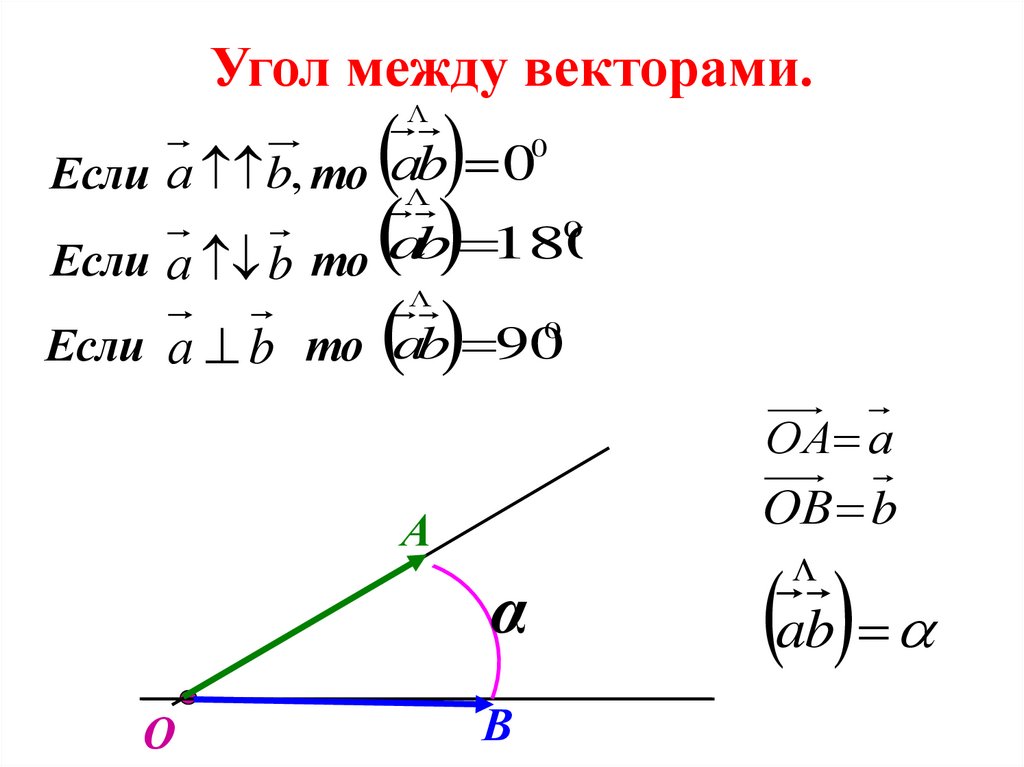
11.
Угол между векторами.Если а b, то а b 0
0
Если а b то ab 90
Если а b то ab 180
0
0
ОА а
ОВ b
А
α
О
В
ab
12.
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между ними.
а
b
a
b
a
b
cos
13.
ab a b cos
Если a b , то
cos90 0 a b 0
0
0
a
b
Если
, то cos
a b a b
180 1
Если а b , то
a b a b
cos0 1
0
2
2
b
a
a
a
a
a
a
Если a b , то a
Скалярное произведение a a называется
скалярным квадратом вектора
14.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
15.
Скалярное произведение векторов.а
b
a
b
a
b
cos
а x1;y1;z1 b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2













 mathematics
mathematics








