Магнитное поле и его характеристики

1. ЭЛЕКТРОМАГНЕТИЗМ

Лекция «Магнитное поле и его
характеристики»

2. Источники магнитного поля

Постоянные магниты;
Электрические токи;
Движущиеся заряды.
Важнейшей особенностью магнитного
поля является то, что оно действует
только на движущиеся в этом поле
электрические заряды

3. Магнитная индукция

Количественная
характеристика
магнитного поля – это вектор магнитной
индукции В. Его используют также в
качестве
силовой
характеристикой,
численно приравнивая максимальному
вращающему моменту, действующему на
рамку с магнитным моментом, равным
единице. В качестве единицы измерения
магнитной индукции в системе СИ
принимают тесла (Тл).

4. Линии магнитной индукции

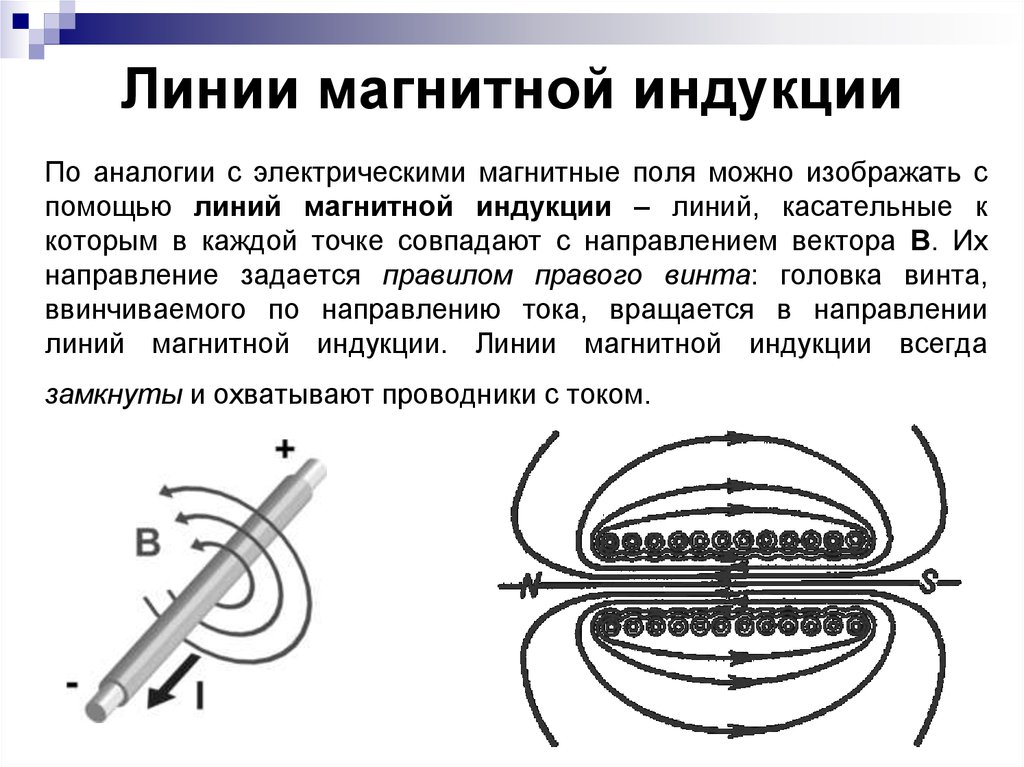
По аналогии с электрическими магнитные поля можно изображать с
помощью линий магнитной индукции – линий, касательные к
которым в каждой точке совпадают с направлением вектора В. Их
направление задается правилом правого винта: головка винта,
ввинчиваемого по направлению тока, вращается в направлении
линий магнитной индукции. Линии магнитной индукции всегда
замкнуты и охватывают проводники с током.

5. Напряженность магнитного поля

В любом теле существуют микроскопические токи, обусловленные
движением электронов в атомах и молекулах. Эти микротоки
создают свое магнитное поле и могут поворачиваться в магнитных
полях макротоков. Вектор магнитной индукции В характеризует
результирующее магнитное поле, создаваемое всеми макро- и
микротоками. Магнитное поле макротоков описывается вектором
напряженности Н. Для однородной изотропной среды вектор
магнитной индукции связан с вектором напряженности следующим
соотношением:
B 0 H ,
где 0 – магнитная постоянная ( 0 = 4π×10-7 Гн/м),
– безразмерная величина – магнитная проницаемость среды,
показывающая, во сколько раз магнитное поле макротоков Н
усиливается за счет поля микротоков среды.
В СИ напряженность магнитного поля измеряют в ампер на метр
(А/м).

6. Закон Био-Савара-Лапласа

Закон
Био–Савара–Лапласа,
с
помощью
которого
рассчитываются магнитные поля, в векторной и скалярной формах
имеет вид соответственно:
0 I dl r
dB
4
r3
где dB – магнитная индукция,
создаваемая
элементарным
проводником dl, по которому
течет ток I, в точке А; – угол
между направлением тока в
проводнике и радиус-вектором
r. Выбор направления (от нас)
вектора индукции объясняется
выше.
0 Idl sin
dB
2
4
r
A dB
r rd R
rd
C
dl
l
I
dl D

7. Расчет индукции МП в вакууме ( = 1) на расстоянии R от конечного (длиной l) или бесконечного прямого проводника с током I

Расчет индукции МП в вакууме ( = 1) на
расстоянии R от конечного (длиной l)
или бесконечного прямого проводника
с током I (рис. выше)
2
2
2
2
1
1
1
1
0 I sin dl
0 I sin rd
0 I
B dB
d
2
2
4 r
4 r sin
4 r
2
2 0 I
0 I
0 I
sin d
( cos )
(cos 1 cos 2 ).
1 4 R
4 R
4 R
1
Для бесконечного провода 1 0, 2 .
В
результате
для
бесконечного
прямого провода с током I имеем
0 I
B
.
2 R

8. Расчет индукции МП в вакууме ( = 1) в центре кругового витка радиусом R с током I

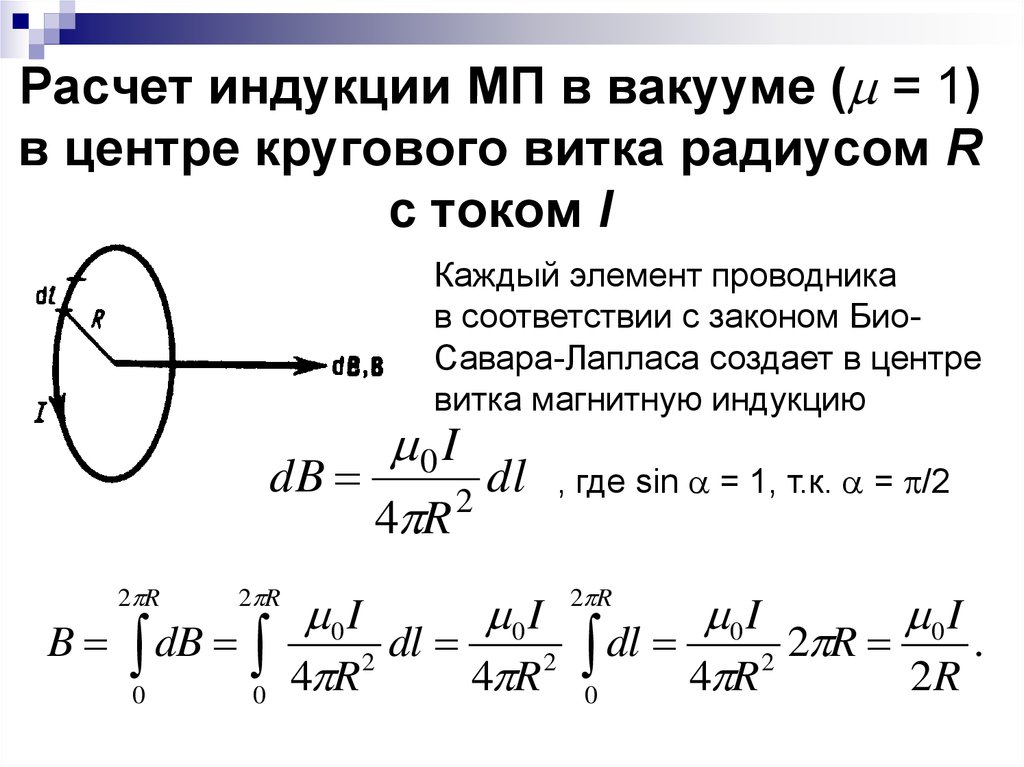
Расчет индукции МП в вакууме ( = 1)
в центре кругового витка радиусом R
с током I
Каждый элемент проводника
в соответствии с законом БиоСавара-Лапласа создает в центре
витка магнитную индукцию
0 I
dB
dl
2
4 R
B
2 R
2 R
0
0
dB
0 I
0 I
dl
2
2
4 R
4 R
, где sin = 1, т.к. = /2
2 R
0 I
0 I
0 dl 4 R 2 2 R 2R .

9. Расчет индукции МП в вакууме ( = 1) на перпендикуляре, восстановленном из центра проводящего кольца радиусом R с током I, на

Расчет индукции МП в вакууме ( = 1) на
перпендикуляре, восстановленном из центра
проводящего кольца радиусом R с током I, на
расстоянии а от плоскости кольца
В силу симметрии вдоль
направления х интеграл
dBx 0.
Согласно построению АЕ равен
половине dBp, откуда
0 IR
dB p 2dB sin 2
dl ,
3
4 r
тогда
R
R
0 IR
0 IR R
0 IR
0 IR 2
B p dB p
dl
dl
R
.
3
3
3
2
2
3
2 r
2 r 0
2 r
2 (R a )
0
0

10. Благодарю за внимание