Similar presentations:
Магнитное поле в вакууме. (Лекция 7)
1.
2.
определениеМагнитным полем называется одна
из форм материи, которая проявляется в силовом воздействии на
двигающиеся электрические заряды,
проводники с током и
постоянные магниты.
3.
камень Геракла (V-III в. до Р.Х.)4.
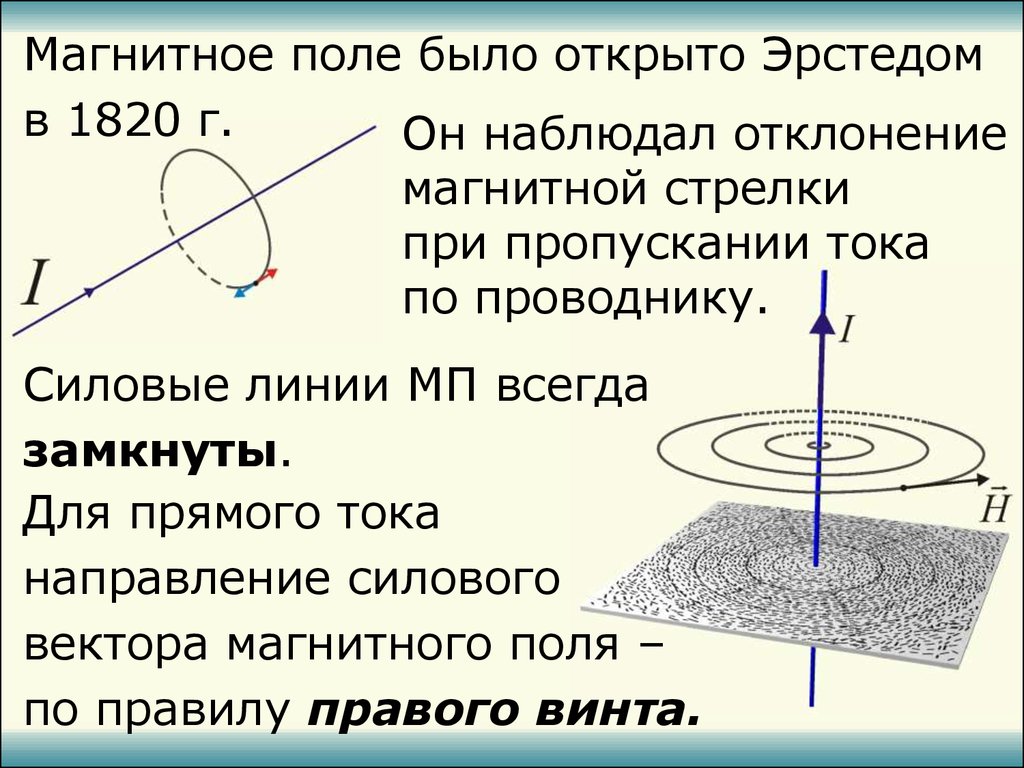
Магнитное поле было открыто Эрстедомв 1820 г.
Он наблюдал отклонение
магнитной стрелки
при пропускании тока
по проводнику.
Силовые линии МП всегда
замкнуты.
Для прямого тока
направление силового
вектора магнитного поля –
по правилу правого винта.
5.
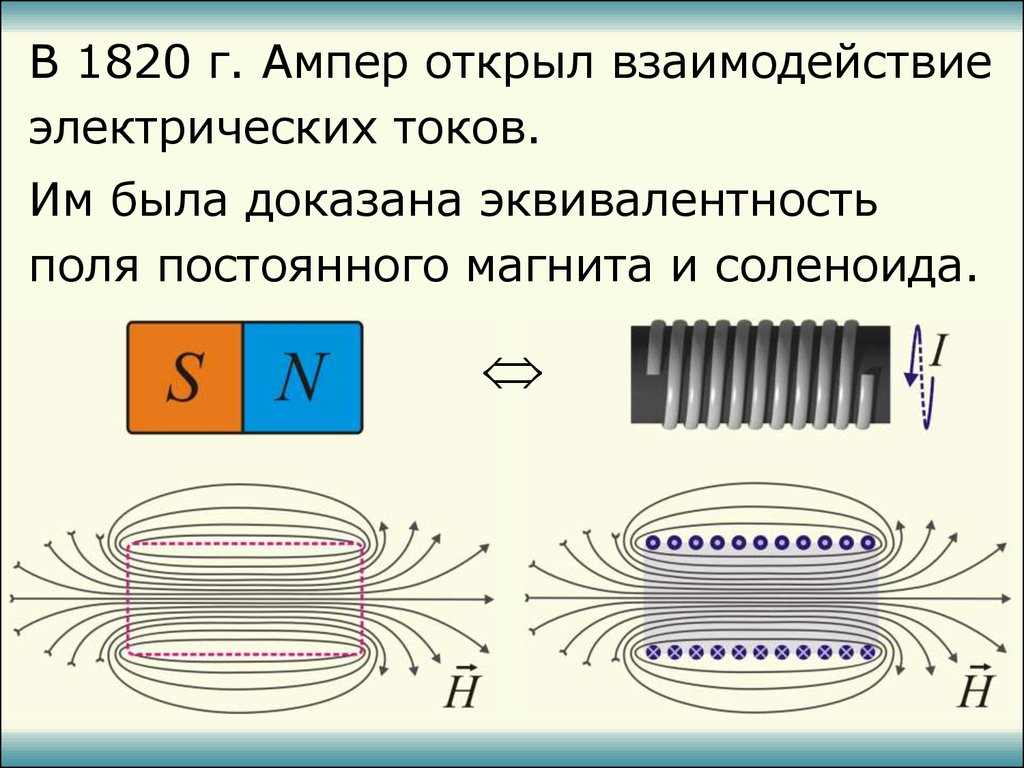
В 1820 г. Ампер открыл взаимодействиеэлектрических токов.
Им была доказана эквивалентность
поля постоянного магнита и соленоида.
6.
Основные выводы1) разделение магнита невозможно
(магнитные заряды не найдены)
2) все магнитные взаимодействия
сводятся к взаимодействию
элементов тока
3) источником магнитного поля
является двигающийся заряд
(переменное электрическое поле)
7. §§ Закон Био-Савара-Лапласа
1820 г., J.B.Biot, F.Savart проводилиизмерение силы dF, с которой элемент
тока IdL действует на магнитный полюс,
удаленный на расстояние r:
dF ~ ( IdL) f1 ( ) f 2 (r )
07
8.
Результаты были проанализированы иобобщены Лапласом (P.Laplace):
1) магнитное поле пропорционально
силе тока;
2) убывает с расстоянием от тока;
3) напряженность поля можно
вычислить суммированием вкладов
от малых элементов тока.
08
9.
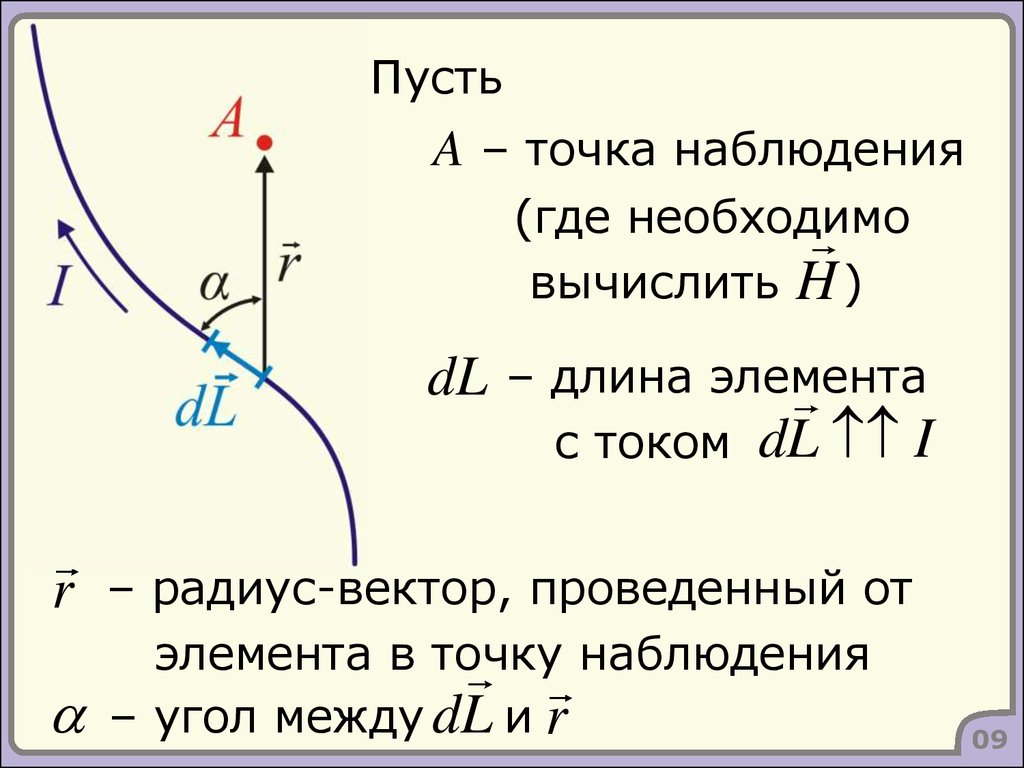
ПустьA – точка наблюдения
(где необходимо
вычислить H )
dL – длина элемента
с током dL I
r
– радиус-вектор, проведенный от
элемента в точку наблюдения
– угол между dL и r
09
10.
ТогдаI dL r
dH A
3
4
r
или
I dL sin
dH A
2
4
r
Закон Био–Савара–Лапласа
в дифференциальной форме
10
11.
– называется напряженностьюмагнитного поля
[H] = 1 А/м (ампер на метр)
H
B
– вектор магнитной индукции
B 0 H
[B] = 1 Тл (Тесла)
– магнитная проницаемость среды
7
Гн/м (генри на метр)
0 4 10
11
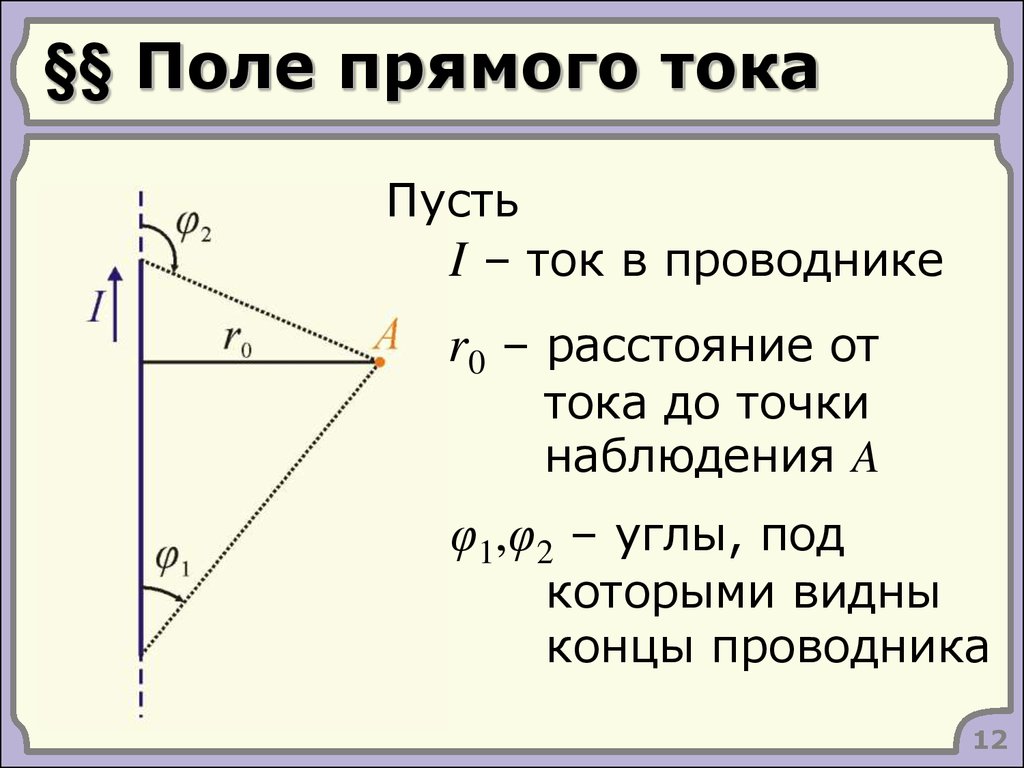
12. §§ Поле прямого тока
ПустьI – ток в проводнике
r0 – расстояние от
тока до точки
наблюдения A
φ1,φ2 – углы, под
которыми видны
концы проводника
12
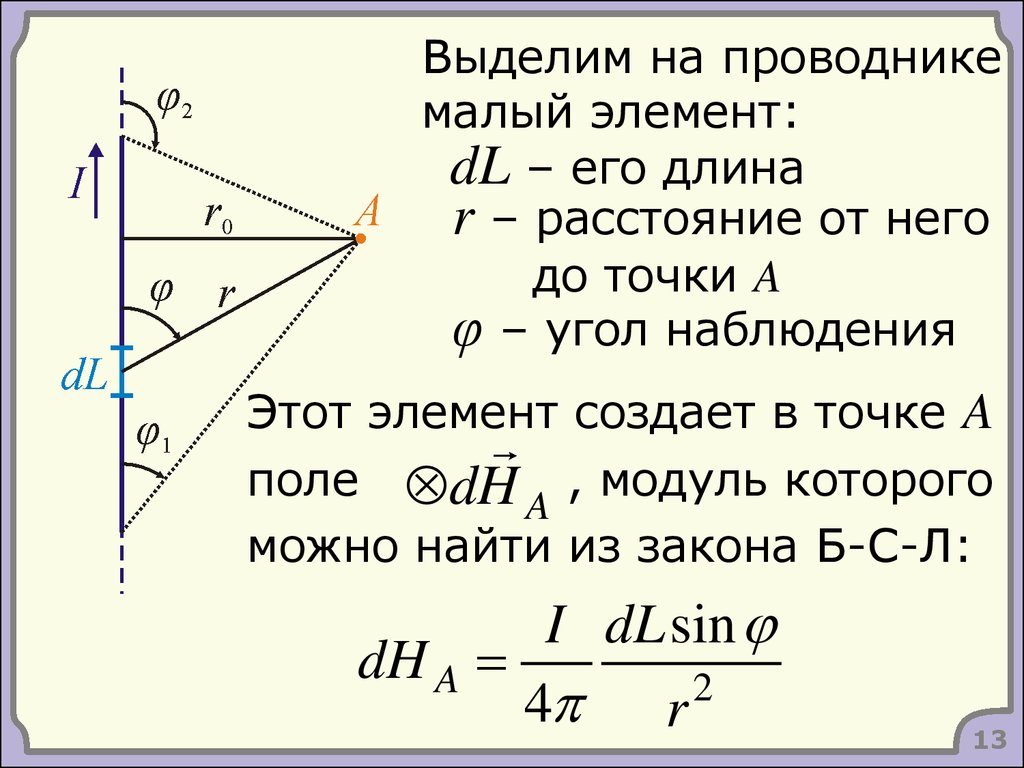
13.
Выделим на проводникемалый элемент:
dL – его длина
r – расстояние от него
до точки A
φ – угол наблюдения
Этот элемент создает в точке A
поле dH A , модуль которого
можно найти из закона Б-С-Л:
I dL sin
dH A
4 r 2
13
14.
r0Из рисунка видно, что r
sin
dL sin r d
следовательно
dH A
I
4 r0
sin d
14
15.
H A dH AI
2
sin
d
4 r0
1
I
cos 1 cos 2
4 r0
При φ1 = 0, φ2 = π получаем поле
бесконечного прямого тока
на расстоянии r0 от него:
HA
I
2 r0
15
16. §§ Магнитное поле кругового витка
I dL sindH
4 r 2
sin 1, dL r
I
dL
H dH
2
4 r
I
H
– поле кругового витка
2r
16
17. §§ Магнитный момент
Рассмотрим поле на оси диполя(r L) r
q
q
E k 2 k
kq
2
2
2
r (r L)
r
(r L)
1 p
1 p 2r
2rL
kq 4
3
4
4
r
0 2 r
0 r
2
2
17
18.
Электрическое смещение на оси диполяна расстоянии r >> L от него
p
D 0E
3
2 r
Рассмотрим круговой виток с током I.
Пусть его радиус – R будет мал, т.е.
будем рассматривать элементарный
ток.
18
19.
Результирующее поле направленовдоль оси x:
I dL sin
dH x
sin
4 r 2
sin 1, dL r
r sin R
I R
dH x
dL
3
4 r
19
20.
pmIS
I R
H x dH x
2
R
3
3
3
4 r
2 r
2 r
pm – магнитный момент контура с током
Для плоского контура
pm ISn
n – нормаль
В произвольном случае
pm I ndS
S
20
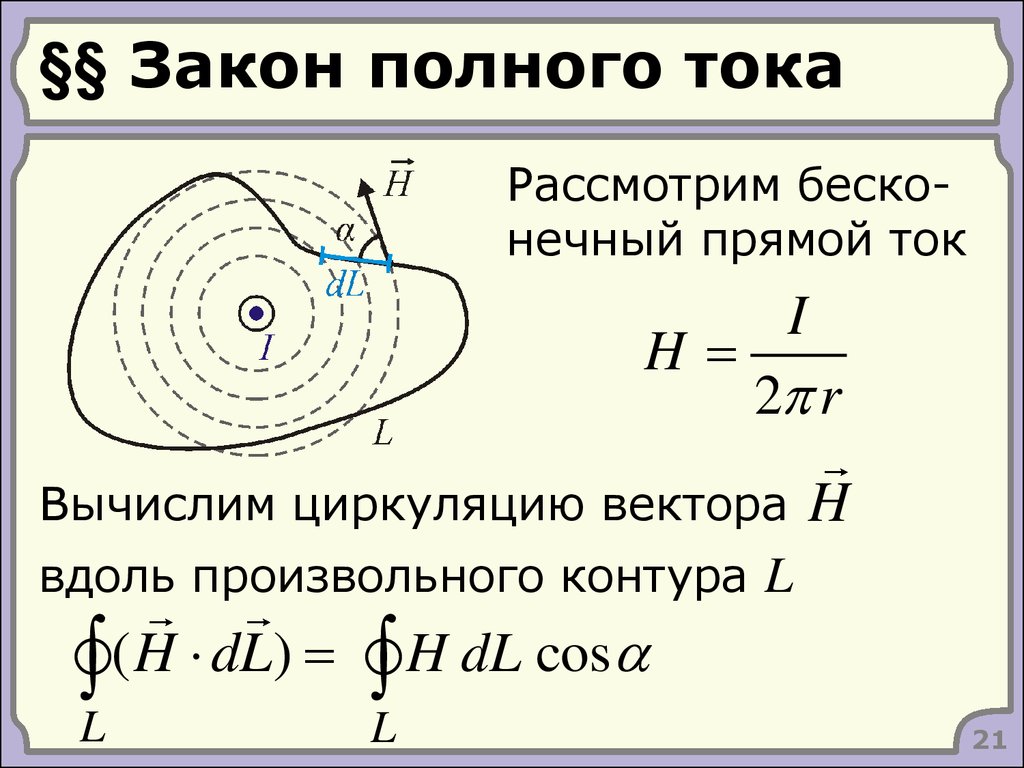
21. §§ Закон полного тока
Рассмотрим бесконечный прямой токH
I
2 r
Вычислим циркуляцию вектора
H
вдоль произвольного контура L
(
H
dL
)
∫
H
dL
cos
∫
L
L
21
22.
rd dL cos2
I
∫ Hr d
d I
2 0
т.е. циркуляция равна
величине тока
Если контур L не охватывает
ток, тогда
I
(
H
dL
)
∫
2
L
2
1
1 2
0
22
23.
Если контур охватывает несколько токов:∫ ( H dL)
L
(
H
dL
)
(
H
dL
)
i
∫
∫
i
L
∫ ( H dL) i Ii
L
Ii
L
i
Закон полного тока
Циркуляция вектора H магнитного поля
постоянного тока вдоль произвольного
замкнутого контура равна алгебраической сумме токов, охватываемых этим
контуром
23
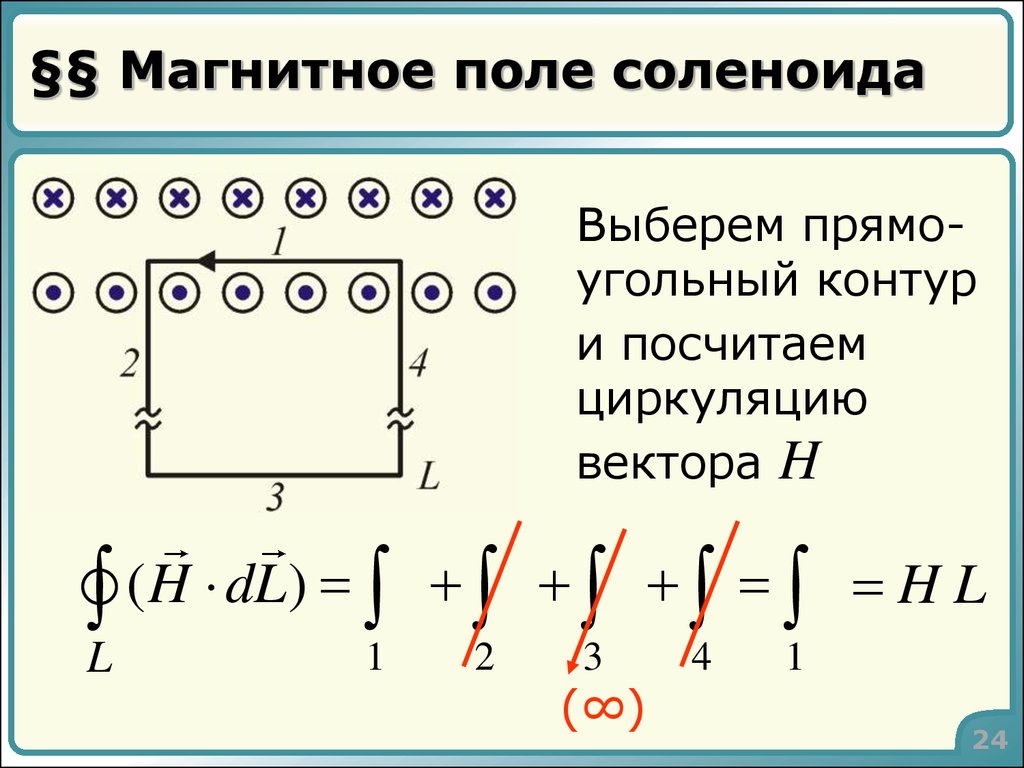
24. §§ Магнитное поле соленоида
Выберем прямоугольный контури посчитаем
циркуляцию
вектора H
(
H
dL
)
H
L
∫
L
1
2
3
(∞)
4
1
24
25.
Если N – число витков, охватываемыхконтуром, то
∫ ( H dL) N I
L
следовательно
N
HL NI H I nI
L
n – плотность намотки витков
Вне соленоида H = 0.
25
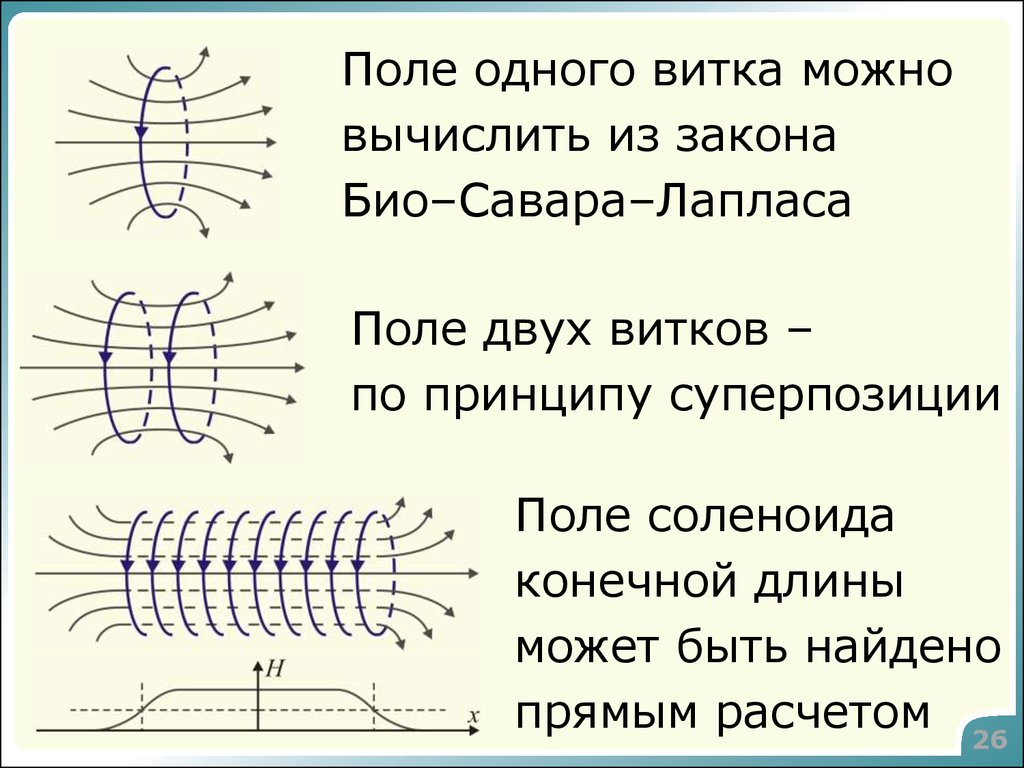
26.
Поле одного витка можновычислить из закона
Био–Савара–Лапласа
Поле двух витков –
по принципу суперпозиции
Поле соленоида
конечной длины
может быть найдено
прямым расчетом 26
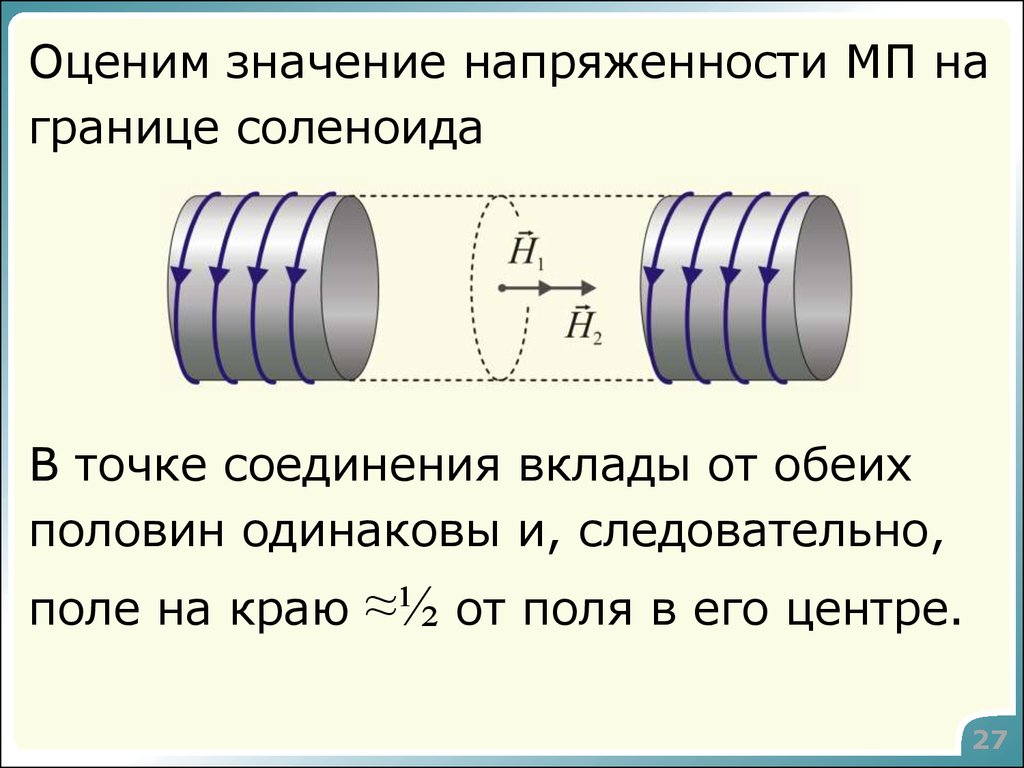
27.
Оценим значение напряженности МП награнице соленоида
В точке соединения вклады от обеих
половин одинаковы и, следовательно,
поле на краю
≈½ от поля в его центре.
27
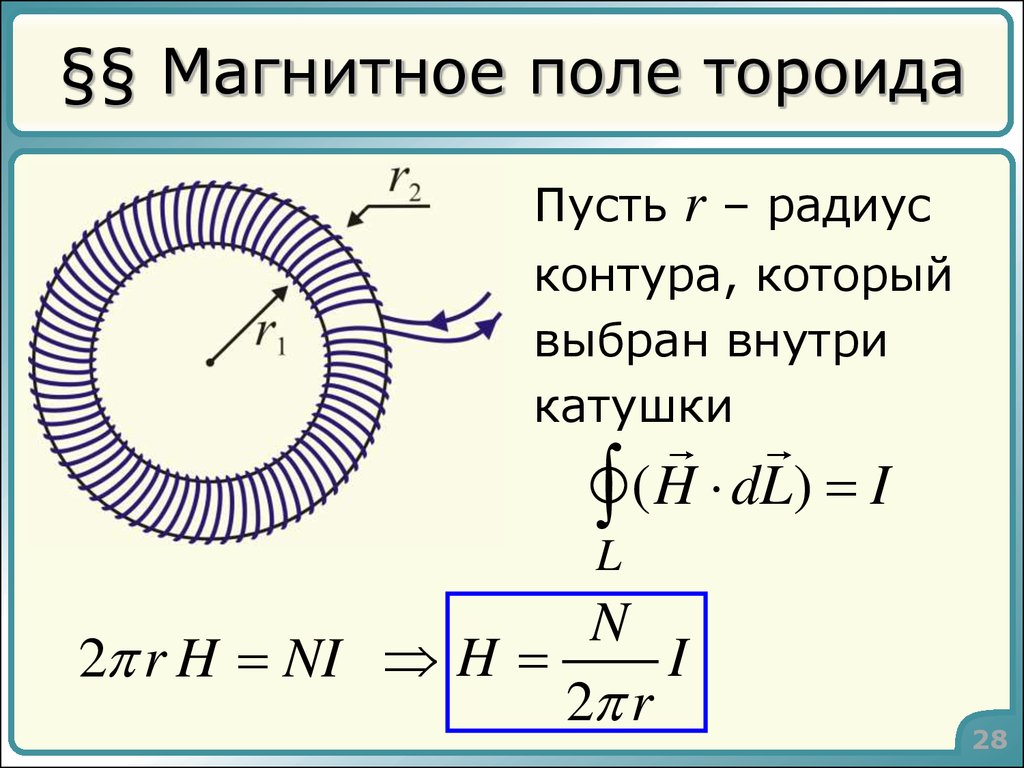
28. §§ Магнитное поле тороида
Пустьr – радиус
контура, который
выбран внутри
катушки
∫ ( H dL) I
L
N
I
2 r H NI H
2 r
28
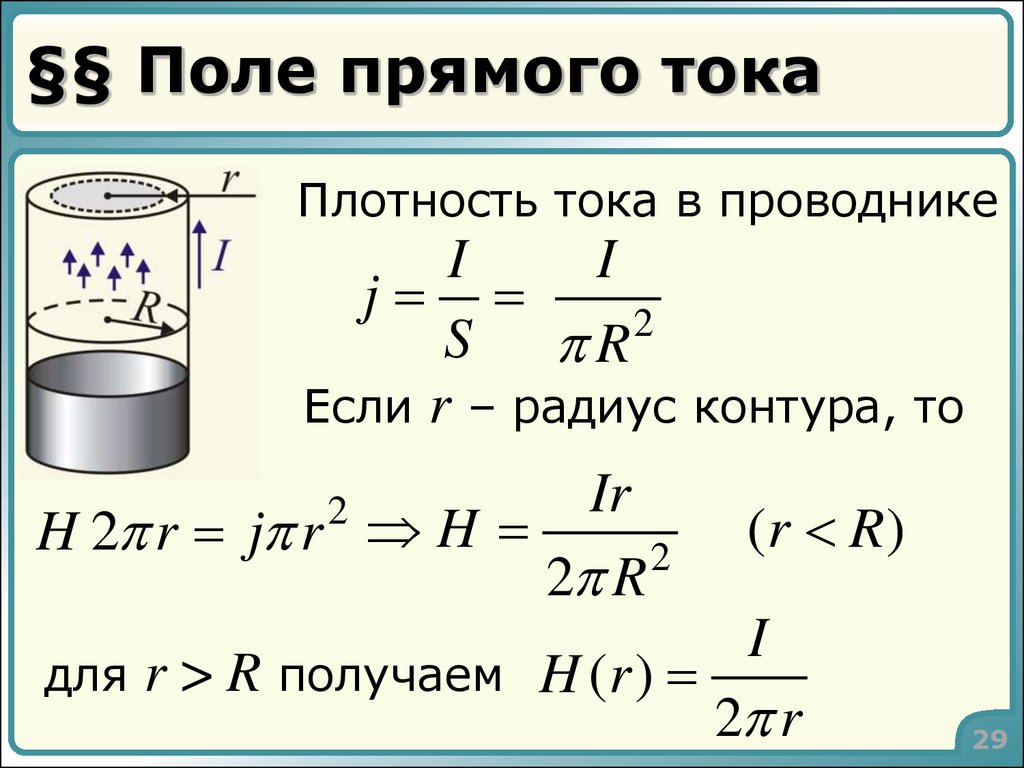
29. §§ Поле прямого тока
Плотность тока в проводникеI
I
j
S R2
Если r – радиус контура, то
Ir
H 2 r j r H
2
2 R
2
для
r > R получаем H (r )
(r R)
I
2 r
29
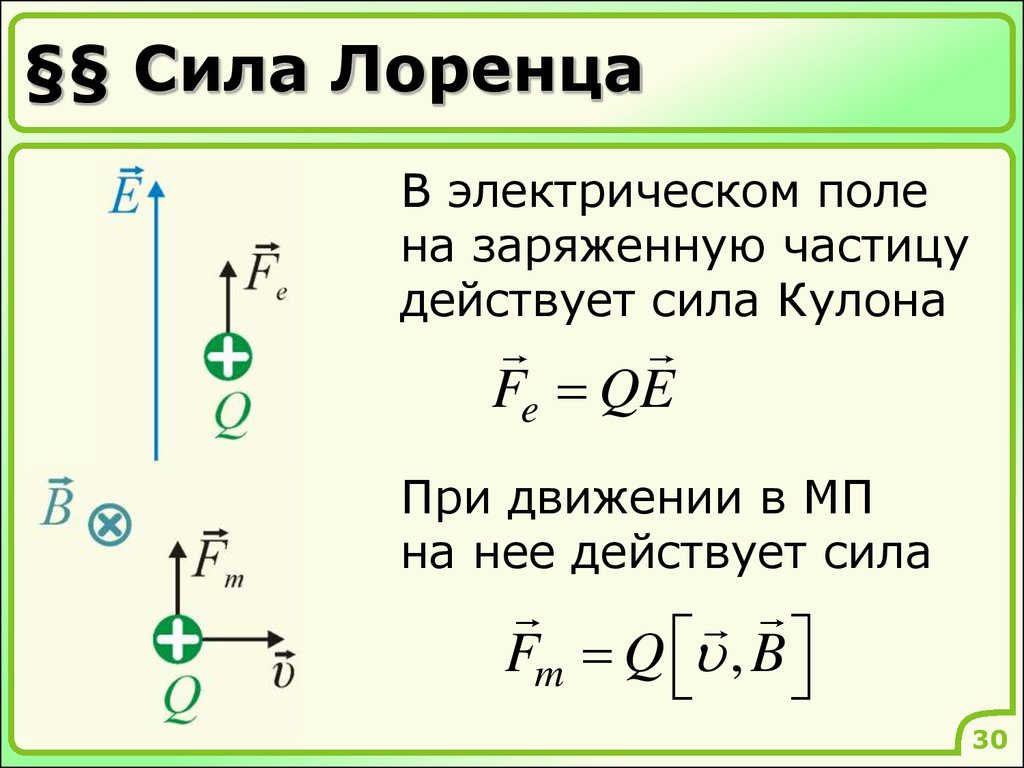
30. §§ Сила Лоренца
В электрическом полена заряженную частицу
действует сила Кулона
Fe QE
При движении в МП
на нее действует сила
Fm Q , B
30
31.
Эта сила вычисляется по правилулевой руки
Модуль силы
Fm Q B sin
где α – угол между
векторами и B .
Сила Лоренца:
F Fe Fm Q E [ , B]
Разделение силы на Э и М составляющие без указания СО смысла не имеет
31
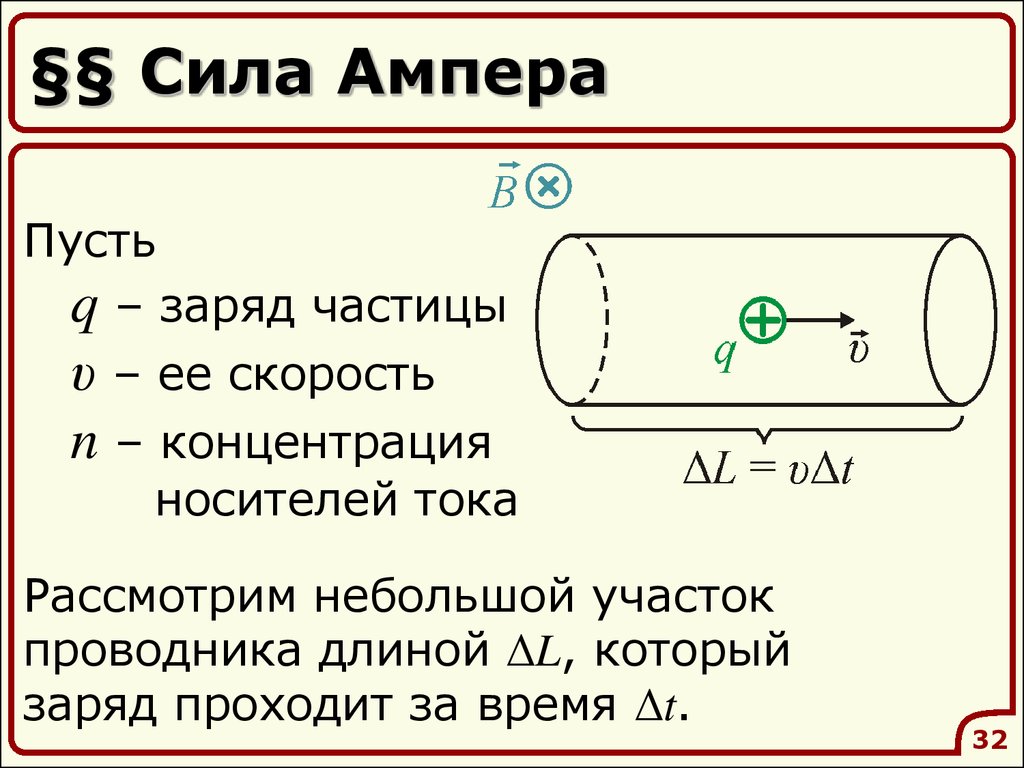
32. §§ Сила Ампера
Пустьq – заряд частицы
υ – ее скорость
n – концентрация
носителей тока
Рассмотрим небольшой участок
проводника длиной ΔL, который
заряд проходит за время Δt.
32
33.
Заряд, проходящий через поперечноесечение проводника
Q n( t S )q
На него действует сила Лоренца
Fm Q , B n( t S )q , B
n q S L, B I L, B
dFA I dL, B – сила, действующая
на элемент тока в м.п.
(сила Ампера) 33
34.
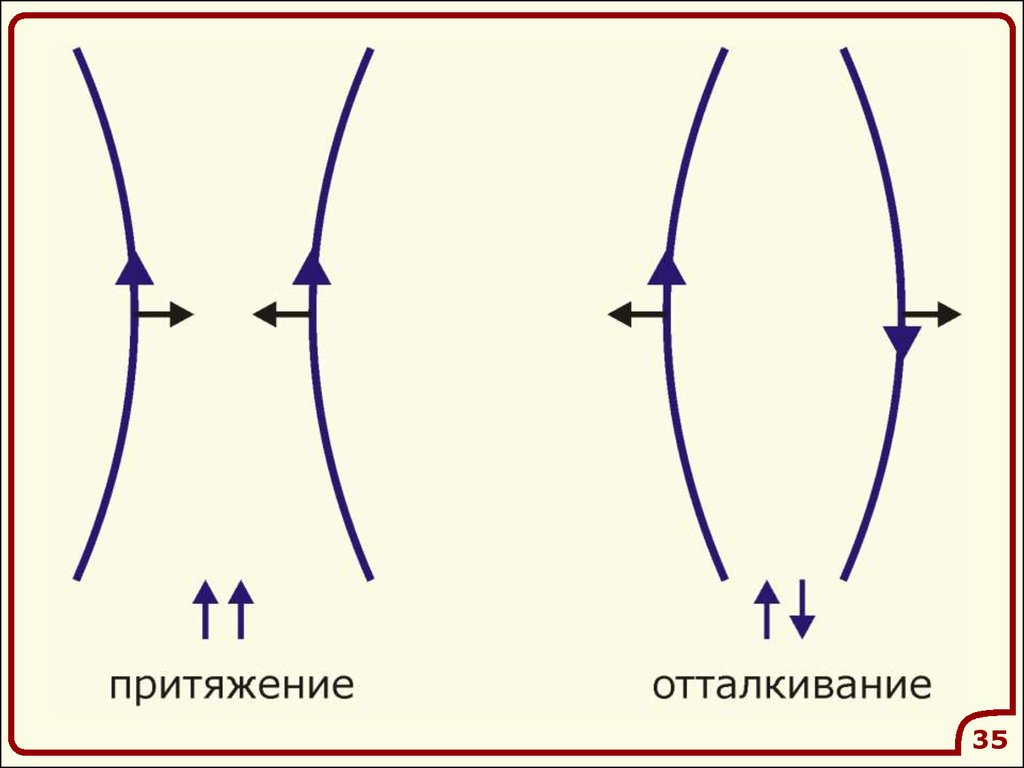
Рассмотрим взаимодействие двухпрямых бесконечных токов
FA I 2 B1 L sin
I1
B1 0
2 r
Сила взаимодействия, в расчете на
единицу длины проводников
I1I 2
FA 0
2 r
0 4 10
7
Гн/м
34
35.
3536. §§ Контур с током в МП
Известно, что прямоугольная рамка стоком поворачивается так, что ее
плоскость располагается перпендикулярно вектору B .
Найдем выражение
для момента сил,
действующих на
рамку в однородном
магнитном поле
36
37.
F1 F3 BIaЭти силы образуют
пару сил, момент
которой:
M F1l F3l ,
где
Тогда
l b sin
M BI ab sin
B IS sin pm B sin( pm , B)
следовательно:
M pm , B
37
38.
Рассмотрим два случая, когда1) векторы
M=0
pm и B параллельны
Выведение рамки
из этого положения
приводит к появлению
вращающего момента,
который стремится
вернуть рамку в
исходное положение.
В этом случае равновесие
будет устойчивым
38
39.
2) векторыpm и B антипараллельны
В этом случае
равновесие будет
неустойчивым
Явление вращения рамки с током в МП
используется при создании электродвигателей и электроизмерительных
приборов.
39
40. §§ Релятивистская природа магнитного поля
Рассмотрим неподвижныйпроводник с током.
При пропускании тока он
остается электронейтральным
n n
Пусть V – скорость заряда Q.
Перейдем в СО, в которой Q неподвижен
V V , V V , υ – скорость дрейфа
40
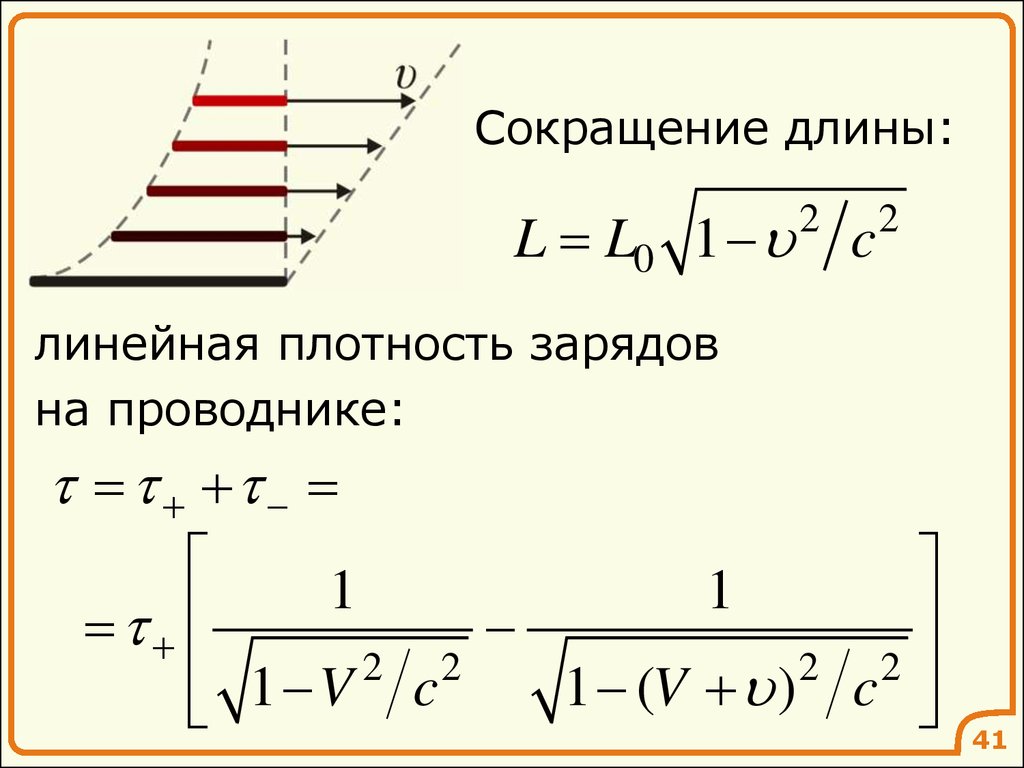
41.
Сокращение длины:L L0 1 c
2
2
линейная плотность зарядов
на проводнике:
1
1
2
2
1 V 2 c 2
1 (V ) c
41
42.
2V2
(V )
1 2 1
2
2c
2c
V
2 2V 2
2c
c
где знак «–» означает, что для Q
проводник является заряженным
отрицательно.
1 2
Поле заряженной нити: E
4 0 r
42
43.
Сила взаимодействия:2
QV
Fk QE Q
2
4 0 r
0c 2 r
QV
I
1
QVB
0
2
2
2
r
0c 0
0 0 c
Сравним полученное выражение с
выражением для силы Лоренца:
Fm Q V , B QVB
43
44.
Выводы:1) МП – релятивистская
поправка к ЭП двигающегося заряда
2) скорость света (электромагнитного
возмущения) в вакууме:
c
1
0 0
299 792 458 м с
44





























 physics
physics








