Similar presentations:
Магнитное поле и его характеристики
1. ЛЕКЦИЯ №2 МАГНИТНОЕ ПОЛЕ И ЕГО ХАРАКТЕРИСТИКИ
2. МАГНИТНОЕ ПОЛЕ
•МАГНИТНОЕ ПОЛЕ – одна из форм проявления электромагнитного поля, отличающаяся тем, что действует толькона движущиеся электрически заряженые частицы и тела,
на проводники с током и тела обладающие магнитным
моментом. Электрическое поле действует как на неподвижные, так и на движущиеся электрические заряды.
•МАГНИТНОЕ ПОЛЕ создается проводниками с током,
движущимися электрически заряженными частицами и
телами с магнитным моментом, отличным от нуля.
3.
• Все постоянные магниты имеют два разноименных полюса: северный и южный.• Одноименные полюса взаимно отталкиваются, а
разноименные взаимно притягиваются.
• Существует магнитное поле Земли, обусловленное, в основном, процессами происходящими в
жидком ядре Земли. Магнитные полюса Земли
не совпадают с географическими (северный магнитный находится около южного географического), угол между осью вращения Земли и линией
Sм
соединяющей магнитные полюса 11,5°.
Sг
Nм
N
S
11,5°
Nг
4.
•Между двумя движущимися друг относительно друга заряженными частицами существуют и электрическое, и магнитноевзаимодействия.
•Опыты показывают, что сила Fмаг, действующая со стороны
магнитного поля на движущуюся в этом поле заряженную
частицу, подчиняется следующим закономерностям:
1)сила Fмаг всегда перпендикулярна вектору скорости υ
частицы;
2)отношение Fмаг/(|q| υ) не зависит ни от заряда q частицы, ни
от модуля ее скорости;
3)при изменении направления скорости частицы модуль силы
Fмаг изменяется от 0 до максимального значения (Fм)макс, которое зависит от значения силовой характеристики магнитного
поля – вектора В, называемого магнитной индукцией поля.
Для графического изображения стационарного, т. е. не изменяющегося со временем, магнитного поля пользуются методом линий магнитной индукции (силовых линий магнит. поля).
5.
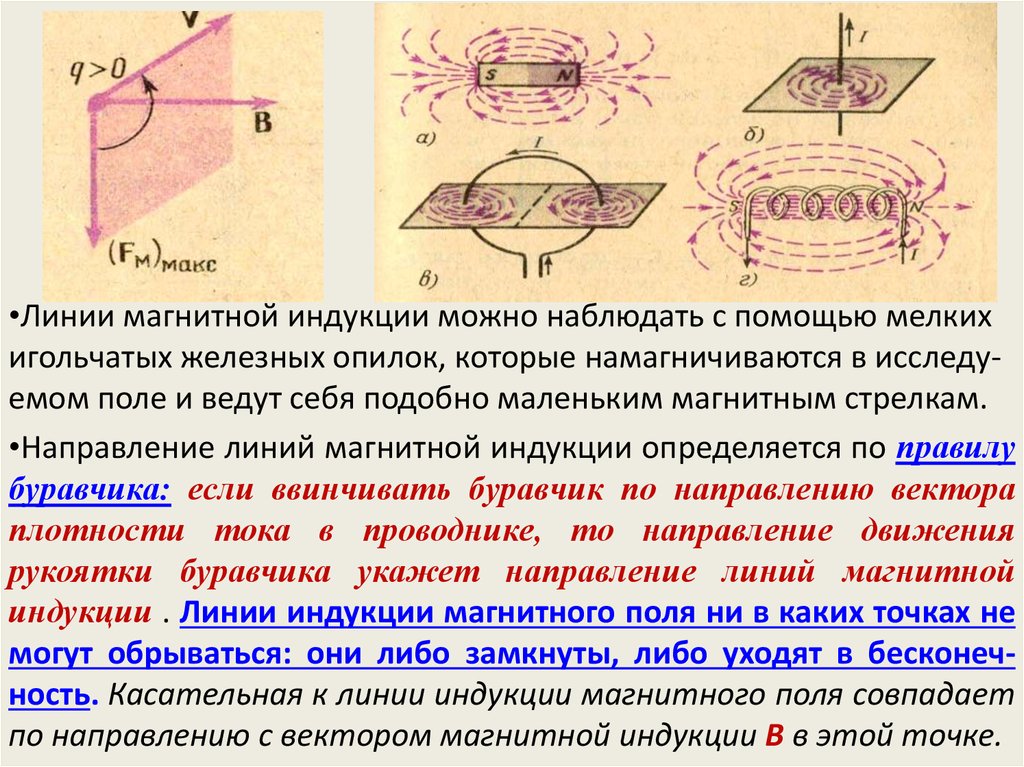
•Линии магнитной индукции можно наблюдать с помощью мелкихигольчатых железных опилок, которые намагничиваются в исследуемом поле и ведут себя подобно маленьким магнитным стрелкам.
•Направление линий магнитной индукции определяется по правилу
буравчика: если ввинчивать буравчик по направлению вектора
плотности тока в проводнике, то направление движения
рукоятки буравчика укажет направление линий магнитной
индукции . Линии индукции магнитного поля ни в каких точках не
могут обрываться: они либо замкнуты, либо уходят в бесконечность. Касательная к линии индукции магнитного поля совпадает
по направлению с вектором магнитной индукции В в этой точке.
6.
•Магнитной индукцией В называется векторная физическаявеличина численно равная максимальной силе (Fм)макс, действующей со стороны магнитного поля на единичный заряд,
движущийся со скоростью υ=1 м/с.
В= (Fм)макс/(|q| υ)
(2.1)
Магнитной индукцией В называется векторная физическая
величина численно равная максимальной силе (Fм)макс, действующей со стороны магнитного поля на проводник единичной длины при токе в нем I=1A.
B= (Fм)макс/(I∙l)
(2.2)
Магнитной индукцией В называется векторная физическая
величина численно равная максимальному вращающему моменту (Мм)макс, действующему со стороны магнитного поля на
замкнутый контур с током с магнитным моментом рm=1 А∙м2.
B= (Мм)макс/рm
(2.4)
7.
МАГНИТНЫЙ МОМЕНТ – векторная величина,pm
характеризующая магнитные свойства тел и
n
частиц тела, для плоского замкнутого электриS
ческого контура численно равная произведеI
нию силы тока I на площадь S, ограниченную контуром,
и направленная перпендикулярно к плоскости контура,
в соответствии с правилом правого винта. n – единичный вектор нормали к площади контура.
(2.5)
pm ISn
Магнитное поле оказывает на рамку с током ориентирующее воздействие,
поворачивая её так, чтобы направление вектора p m совпало с направлением вектора
магнитной индукции В, т. е. плоский замкнутый контур
с током ведет себя в магнитном поле также, как и магнитная стрелка.
8. СИЛА ЛОРЕНЦА. ЗАКОН АМПЕРА.
•В общем случае сила, действующая со стороны магнитногополя на движущуюся в нем заряженную частицу (магнитная
составляющая силы Лоренца), определяется по формуле:
(2.6)
FË Q [ B]
FË Q B sin (2.7)
где α- угол между векторами и B .
Сила FË направлена перпендикулярно скорости заряженной
частицы и сообщает частице только нормальное ускорение.
Эта сила не совершает работы и вызывает лишь искривление
траектории частицы. Поэтому при движении свободной заряженной частицы в магнитном поле ее кинетическая энергия не
изменяется.
FË Q E Q[ B] Q{E [ B]}
(2.8)
9.
•Разделение силы Лоренца на электрическую и магнитнуюсоставляющие относительно, т. е. эти составляющие зависят
от выбора инерциальной системы отсчета. При переходе от
одной инерциальной системы отсчета к другой изменяются
не только скорость заряженной
частицы, но также и си
ловые характеристики E и B . Соответственно разделение
электромагнитного поля на электрическое и магнитное поля
тоже относительно.
•На проводники с электрическим током, находящиеся в
магнитном поле, действуют силы Ампера.
•Сила Ампера dF, приложенная к малому элементу проводника с током I, равна геометрической сумме сил, которые
действуют со стороны магнитного поля на движущиеся в проводнике носители тока.
(2.9)
dF qe n0 S dl[ B] I [dl B]
10.
•Формула (2.9) выражает закон Ампера:Сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника на магнитную индукцию поля.
dF=I∙dl∙B∙sinα
(2.10)
Сила Ампера, действующая в магнитном поле на проводник
конечной длины l с током I , равна геометрической сумме
сил Ампера, действующих на все малые элементы этого
проводника:
(2.11)
F I [dl B]
(l )
11.
•Магнитное поле оказывает ориентирующее действие на замкнутый проводящий контур, по которому идет постоянныйэлектрический ток.
Результирующий вращающий момент М, действующий на
рамку (контур) с током, равен моменту пары сил:
М=I∙a∙b∙B∙sinβ =I∙S∙B∙sinβ =pm∙B∙sinβ .
(2.12)
M [ pm B]
(2.13)
Если контур с током находится в неоднородном магнитном
поле, то действие сил Ампера на контур не сводится только к
результирующему вращающему моменту (2.13). В этом случае
на контур действует еще и результирующая сила:
12.
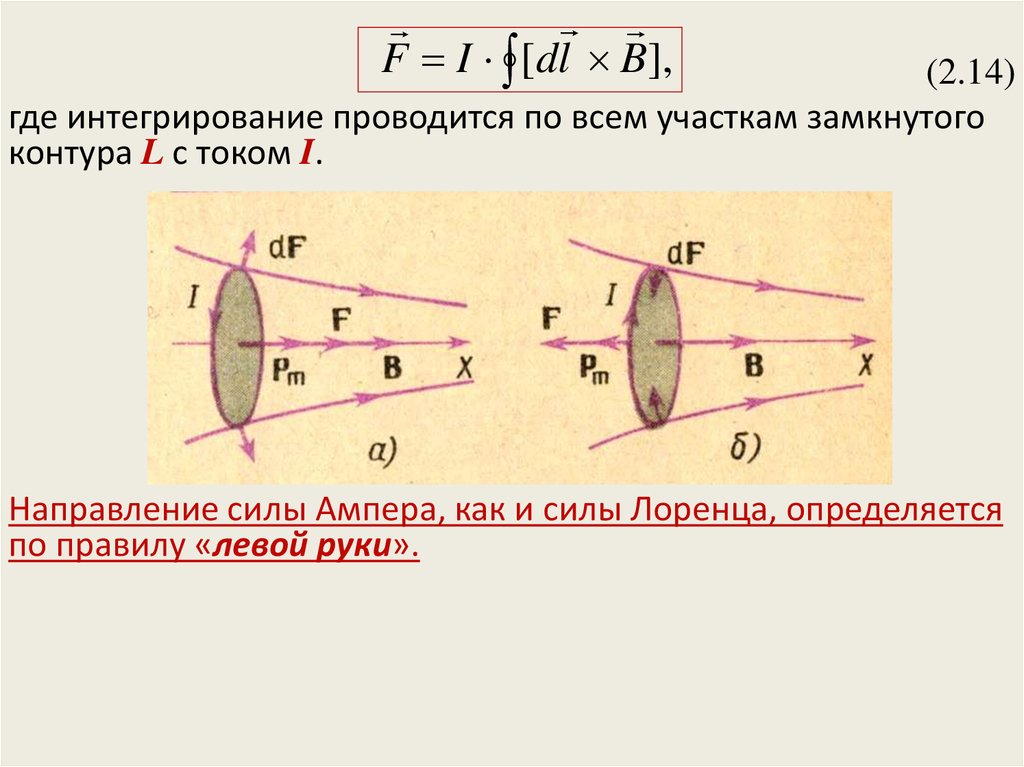
F I [dl B],(2.14)
где интегрирование проводится по всем участкам замкнутого
контура L с током I.
Направление силы Ампера, как и силы Лоренца, определяется
по правилу «левой руки».
13. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ
Ампер (1775-1836) предположил, что в любом теле существуют микроскопические токи обусловленные движением электронов в атомах и молекулах. Эти микротоки обладают собственными магнитными моментами исоздают своё магнитное поле.
Если вблизи тела поместить проводник с током (макроток), то под действием его магнитного поля, микротоки
во всех атомах определенным образом ориентируются,
создавая в теле дополнительное магнитное поле. Магнитная индукция B характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками.
То есть: при одном и том же токе и равных условиях,в
различных средах значения вектора магнитной индукции B будут иметь различные значения.
14.
Магнитное поле макротоков описывается ВЕКТОРОМНАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ H . Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности соотношением:
(2.15)
B 0 H
7 Гн
0 4 10
– магнитная постоянная.
м
– магнитная проницаемость среды, показывающая
во сколько раз магнитное поле макротоков H усиливается за счет магнитного поля микротоков среды.
Сравнивая векторные характеристики электростатическокого E, D и магнитного H , B полей, можно заметить
что аналогом вектора электрического смещения D является вектор напряженности магнитного поля H , а аналогом вектора напряженности электрического поля E ,
является вектор магнитной индукции B .
15. ЗАКОН БИО – САВАРА – ЛАПЛАСА
Магнитное поле постоянного тока изучалось французами Био (1774-1862) иСаваром (1791-1842), Лапласом результаты их экспериментальных исследований были проанализированы и обобdl
щены с учетом принципа суперпозиции.
dB
Для проводника с током I, элемент которого dl создает в некоторой точке C магнитное поле с индукцией dB, было получено соотношение:
0 I [dl r ]
dB
(2.16)
4
r3
dl – вектор равный по модулю длине проводника dl и совпадающий по направлению с током I, r – радиус-вектор,
проведенный из элемента проводника dl в точку C поля.
16.
Направление dB перпендикулярно dl и r, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линиям магнитной индукции. Это направлениеможет быть найдено с помощью правила правого винта, где
направление вращения головки dB поступательное движение
винта – направление тока I.
Закон Био – Савара – Лапласа в скалярной форме
(2.17)
0 Idl sin
dB
4
r2
– угол между векторами dl и r .
Для магнитного как и для электрического полей справедлив
ПРИНЦИП СУПЕРПОЗИЦИИ: Магнитная индукция, создаваемая в одной точке несколькими движущимися зарядами или
токами, равна векторной сумме магнитных индукций, создаn
ваемых каждым током (зарядом) в отдельности.
B Bi
i 1
17.
0 I0 I
B
sin d
(cos 1 cos 2 )
4 r0
4 r0
2
1
0 8I a 2 b 2
B
4
a b
18.
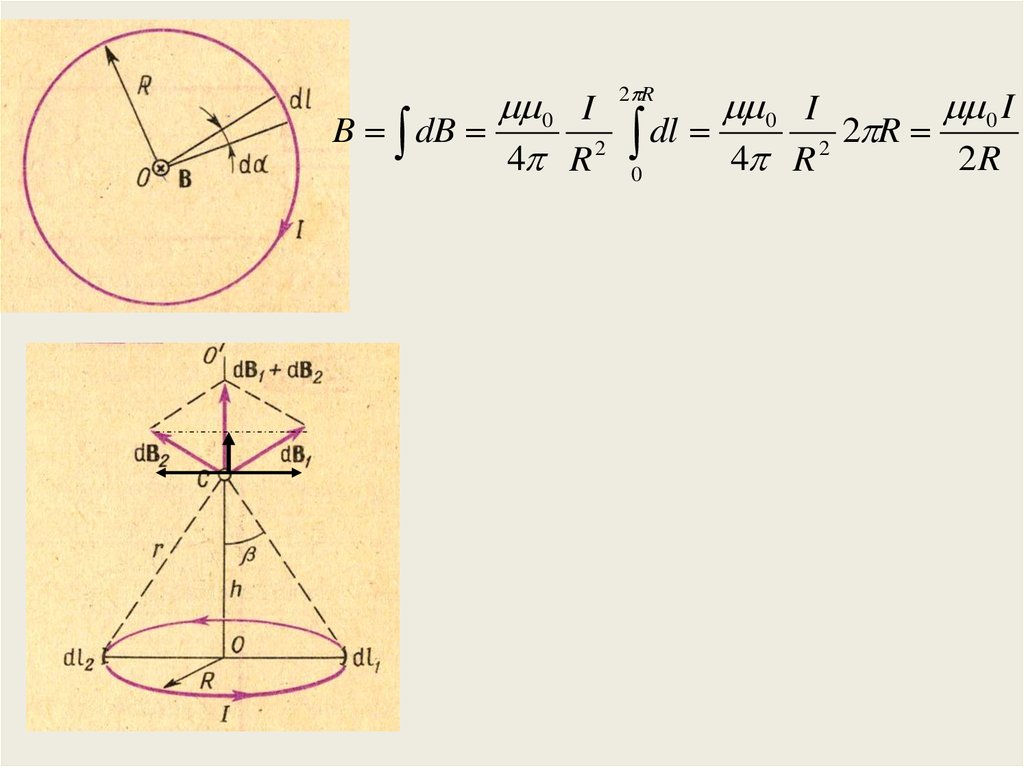
0 IB dB
4 R 2
2 R
0 I
0 I
0 dl 4 R 2 2 R 2R
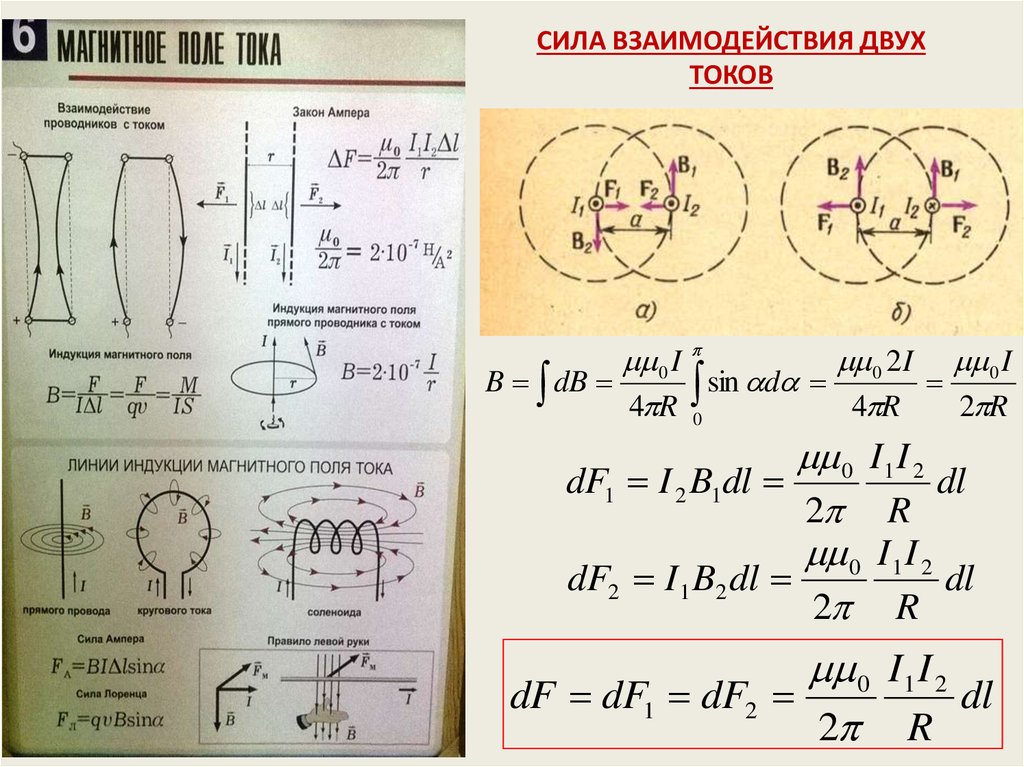
19. СИЛА ВЗАИМОДЕЙСТВИЯ ДВУХ ТОКОВ
0 I0 2I 0 I
B dB
sin
d
4 R 0
4 R
2 R
0 I1 I 2
dF1 I 2 B1dl
dl
2 R
0 I1 I 2
dF2 I1 B2 dl
dl
2 R
0 I1 I 2
dF dF1 dF2
dl
2 R
20. МАГНИТНАЯ ПОСТОЯННАЯ. ЕДИНИЦЫ ИЗМЕРЕНИЯМАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
Если два параллельных проводника с токами находятсяв вакууме 1 , то сила их действия на единицу
проводника: dF 2I I
dl
0
4
1 2
R
Для определения численного значения магнитной постоянной 0 , воспользуемся определением ампера
(единицы измерения силы тока), согласно которому:
АМПЕР- сила неизменяющегося тока, который при
прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно
малого поперечного сечения, расположенного в
21.
вакууме на расстоянии 1 м один от другого, создаётмежду проводниками силу равную 2*10⁻⁷ Н на каждый метр длины.
Следовательно, если I1 I 2 1( A) и R 1( м) то
dF
2 10 7 ( H м)
dl
dFR4
7 1 4
7 H
7 Гн
0
2 10
4 10 ( 2 ) 4 10 ( )
2 1 1
м
dl 2 I 1 I 2
A
Гн
0 4 10 ( )
м
7
Где Гн (генри) единица индуктивности (НЕ ИНДУКЦИИ!!)
22.
Единица измерения магнитной индукции – Тл (Тесла).1 Тл – магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый
метр прямого перпендикулярного полю проводника
с током 1 А.
Н
1Тл 1
А м
Единица измерения напряженности магнитного поля –
А/м (ампер/метр).
1 А/м – напряженность такого поля, магнитная индукция которого в вакууме 4π·10¯⁷ Тл.
23. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА
24.
Каждый проводник с током создает в пространстве магнитное поле. Ток – упорядоченное движение электрических зарядов. Значит любой движущийся заряд создает вокруг себя магнитное поле.Свободно двигающийся заряд q ( заряд двигающийся с
постоянной нерелятивистской скоростью v ), создает в
точке М, на расстоянии r магнитное поле с индукцией
B
.
М
0 qv r
r
B
3
q
4 r
v
Вектор B направлен перпендикулярно плоскости
в которой расположены r и v . Его направление – поступательное движение правого винта, при его вращении
от v к r .
25.
Формула магнитной индукции свободно двигающегосязаряда в скалярной форме:
0 qv
B
sin
2
4 r
Движущийся заряд по своим свойствам эквивалентен
элементу тока
Idl qv
Эти закономерности справедливы только при малых
скоростях движущегося заряда, когда электрическое
поле свободно двигающегося заряда можно считать
электростатическим , то есть неподвижным зарядом в
той точке в которой находится двигающийся заряд.





















 physics
physics








