Магнитное поле и его характеристики. Лекция 4

1.

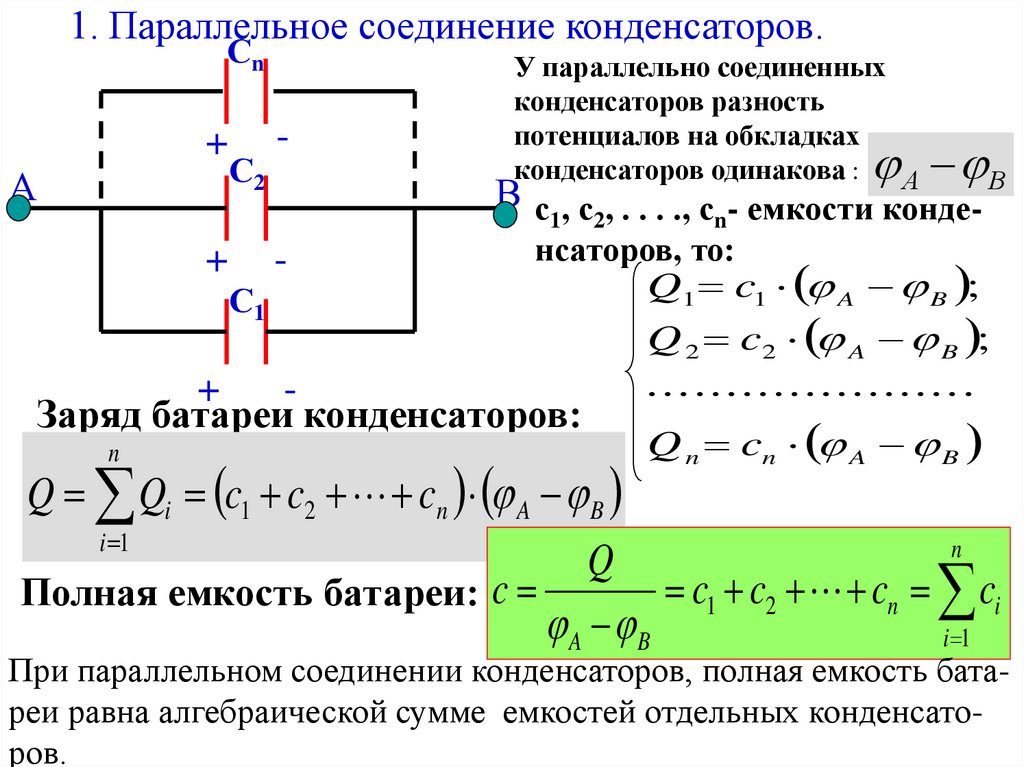
1. Параллельное соединение конденсаторов.
Сn
+
А
С2
-
У параллельно соединенных
конденсаторов разность
потенциалов на обкладках
конденсаторов одинакова :
А
В с , с , . . . ., с - емкости конде1
+
С1
2
n
нсаторов, то:
Q1 c1 A B ;
+
Заряд батареи конденсаторов:
n
В
Q 2 c2 A B ;
Q n cn A B
Q Qi c1 c2 cn A B
i 1
n
Q
c1 c2 cn ci
Полная емкость батареи: c
A B
i 1
При параллельном соединении конденсаторов, полная емкость батареи равна алгебраической сумме емкостей отдельных конденсаторов.

2.

2. Последовательное соединение конденсаторов.
1
2
n
+ -
+ -
+с -
с1
с2
n
Заряды всех обкладок
равны по модулю. Разность
потенциалов на зажимах
батареи:
Q
i , i , с другой стороны
i 1
ci
n
n
Q
1
Q
C
i 1 ci
n
1
1
С I 1 ci
При последовательном соединении конденсаторов
суммируются величины, обратнные емкостям.

3.

Правила Кирхгофа.
Применяются для расчета параметров замкнутых электрических цепей,
содержащих разветвления.
Точка, где сходятся три или больше прово1-узел
I 3 дника, называется узлом.
I1
Контур-любой замкнутый участок цепи.
2: 2 , R 2 , R 3 , 3
1: 1, R1 , R 2 , 2
2 ,r
+
I1
3
3: 1, R1 , R ,
3
3
Расставляем токи в отдельных участках цепи,
с указанием их предполагаемых направлений.
Выбираем направление обхода контуров.
Сумма токов, сходящихся
в узле, равна нулю:
n
I 0
i 1
+
2
-
1
R3
3,r
+
-
1 , r
I2 I3
R2
R1
I1
I2
2-узел I 3
I 2 I1 I 3 0
i
Сумма падений напряжений на элементах
контура должна равняться сумме ЭДС,
действующих в контуре:
1 : I1 r1 I1 R1 I 2 R2 I 2 r2 1 2
2 : I 2 r2 I 2 R2 I 3 R3 I 3 r3 2 3
n
l
I R
i 1
i
i
k 1
k

4. Лекция 4. Магнитное поле и его характеристики

1. Магнитное поле и его характеристики.
2. Закон Био-Савара-Лапласа.
3. Контур с током в магнитном поле. Работа
перемещения проводника с током в
магнитном поле.
4. Сила Лоренца. Движение заряженных частиц
в магнитном поле.
5. Магнитные моменты электронов и атомов.
Магнитная проницаемость. Диа- и
парамагнетики. Ферромагнетики.

5. 1. Магнитное поле и его характеристики. Магнитное поле - форма существования материи, окружающей движущиеся электрические

заряды
(проводники с током, постоянные магниты).
Линии магнитной индукции всегда замкнуты, что
говорит об отсутствии в природе магнитных
зарядов и вихревом характере магнитного поля.

6.

Силовые линии магнитной индукции.
Непрерывные линии, касательные к которым в каждой точке,
через которую они проходят, совпадают с вектором индукции,
называются силовыми линиями магнитного поля.
Свойства силовых линий магнитного поля:
1. Замкнуты, не имеют ни начала, ни конца.
2. Линии непрерывны, не пересекаются.
3. Густота линий выбирается так, чтобы количество линий, пронизывающих
единицу поверхности площадки, перпендикулярной к линиям, было равно
численному значению вектора B .
Направление линий - правило правого винта: винт вкручивается по направлению
тока, головка винта вращается в направлении линий магнитной индукции.
I
B
B

7.

Направление линий определяется правилом
правого винта.
Соленоид - катушка с током, витки которой
расположены вплотную друг к другу, а диаметр
витка много меньше длины катушки.
Магнитное поле внутри соленоида является
однородным. Магнитное поле называется
однородным, если вектор B в любой точке
постоянен.

8.

I
S
B
Магнитное поле
прямого тока
Магнитное поле
соленоида с током
N
Магнитное поле
полосового магнита
Однородное поле
Силовая линия
B
N
S

9.

Принцип суперпозиции: индукция
магнитного поля, создаваемого несколькими
токами или движущимися зарядами, равна
векторной сумме индукций магнитных полей,
создаваемых каждым током или зарядом:
В Вi

10.

Сила dF , с которой магнитное поле действует на
элемент проводника с током dl находящийся в
магнитном поле, прямо пропорциональна силе
тока I и векторному произведению элемента
длины dl на магнитную индукцию В :
I
dl
B
dF
dF BIdl sin - закон Ампера

11.

Направление вектора dF
Правило левой руки: если ладонь левой руки расположить так, чтобы
магнитные силовые линии входили в нее, а 4 вытянутых пальца направить по
току, то отогнутый большой палец покажет направление силы.
Сила, действующая на провод конечной длины
При I = const, B=const, F = B L I sin
Если =900, F = B L l
F
В
I l
Н
B 1
1Тл
А м

12.

Индукция магнитного поля - векторная физическая величина, численно равная
силе, действующей в однородном магнитном поле на проводник единичной длины
с единичной силой тока, расположенный перпендикулярно магнитным силовым
линиям.
Магнитное
поле
макротоков
описывается
вектором
магнитной
напряженности .
Для однородной изотропной среды: B H H B , H 1 A
н
0
0
м
0= 4 10-7Гн/м - магнитная постоянная,
- магнитная проницаемость среды, показывающая, во сколько
раз магнитное поле изменяется в данной среде.

13.

Поток вектора В
(магнитный поток) через площадку dS - скалярная величина, равная
dS
dS n
dФB BdS Bn dS ,
B
Bn - проекция на направление нормали к площадке;
- угол между векторами В и п
Bn B cos
dS - направленный элемент поверхности,
dS dSn.

14.

Ф 1Тл м 1Вб
2
ФВ ВS cos ; если 0, ФВ ВS
S
B
B
n
B 0
В
S
S
BS
n
B
BS cos
Магнитный поток через поверхность S численно равен количеству
магнитных силовых линий, пересекающих данную поверхность.
ФB BdS 0
- теорема Гаусса: поток вектора магнитной индукции
через любую замкнутую поверхность равен нулю (в
природе отсутствуют магнитные заряды).

15.

Закон Био-Савара-Лапласа: каждый
элемент dl проводника с током I
создает магнитное поле, вектор
индукции которого d B в некоторой
произвольной точке определяется
по формуле:
0 Idl sin
dB
4
r2
I
dB
с током;
dl - элемент проводника, сонаправленный
dl c точкой K;
r - радиус-вектор, соединяющий
- угол между dl и r
dl
r

16.

А. Магнитное поле в центре кругового тока:
I
B r
B r
B
dl
0 I
2r
Б. магнитное поле прямолинейного проводника с током.
1) для проводника конечной длины:
B
1
r0
2
I
2) для проводника бесконечной длины: 1 = 0, 2 = :
B
3) Поле внутри длинного соленоида с током:
B= 0nI
где n - число витков на единице длины.
Ø
0 I
(cos 1 cos 2 )
4 r0
+ ll
_Ø
0 I
2 r0

17.

3. Контур с током в магнитном поле. Работа перемещения
проводника с током в магнитном поле.
Магнитный момент контура с током - это векторная физическая
величина численно равная произведению силы тока на площадь
контура.
p m I S n,
pm 1А м 2
п - единичный вектор внешней нормали к поверхности S, ограниченной контуром с током.
+Ø Ø -
I
n
pm
.
I
pm
I
pm
момент стремится привести контур в
Вращающий
положение устойчивого равновесия, при котором
М pm B
векторы p m и
В
сонаправлены.

18.

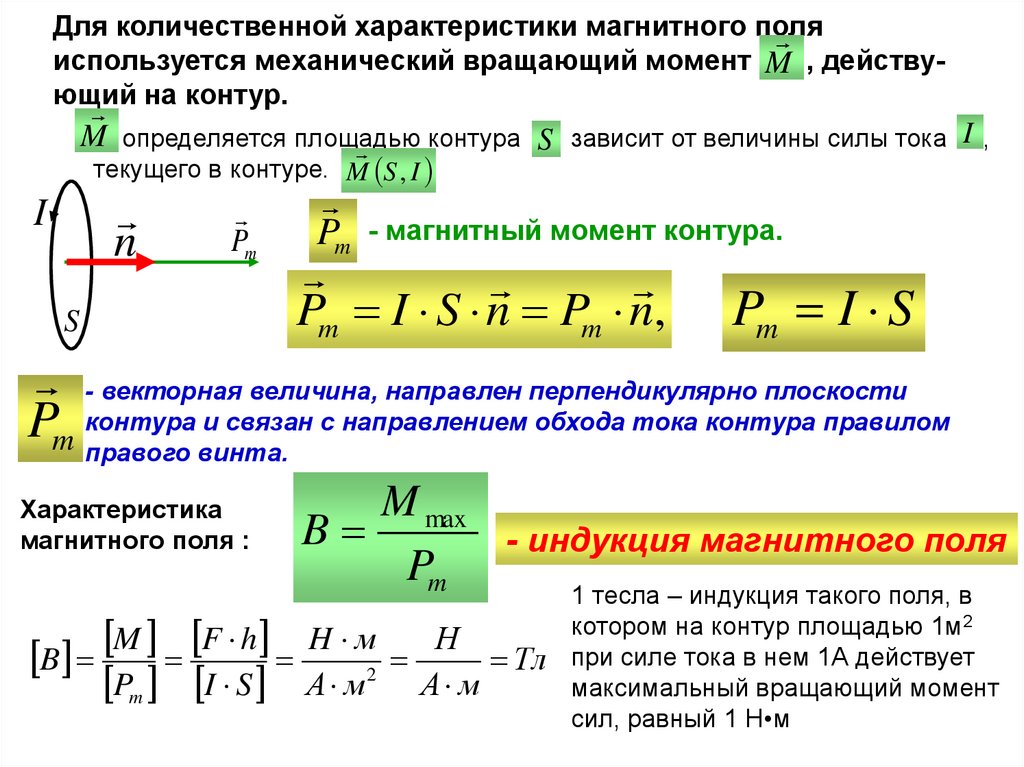
Для количественной характеристики магнитного поля
используется механический вращающий момент M , действующий
на контур.
M определяется площадью
контура S , зависит от величины силы тока I ,
текущего в контуре. M S , I
n
I
Pm
S
Pm - магнитный момент контура.
Pm I S n Pm n,
Pm I S
- векторная величина, направлен перпендикулярно плоскости
и связан с направлением обхода тока контура правилом
Pm контура
правого винта.
Характеристика
магнитного поля :
M max
B
Pm
- индукция магнитного поля
B M F h H м2 Н Тл
Pm I S А м А м
1 тесла – индукция такого поля, в
котором на контур площадью 1м2
при силе тока в нем 1А действует
максимальный вращающий момент
сил, равный 1 Н•м

19.

Работа, совершаемая силами Ампера при перемещении замкнутого контура
с током в магнитном поле, равна произведению силы тока на изменение
магнитного потока, сцепленного с контуром:
A I m

20.

4. Сила Лоренца. Движение заряженных частиц в магнитном поле.
.
-
.
+
.F
л
FЛ q B
.B .
Fл
.
.
.
.
1. Движение заряженной частицы вдоль силовой линии, B
B
+
FЛ qVB sin 00 0
2. Движение заряженной частицы перпендикулярно силовым линиям, B
q B m
B
Fл
+
Fл
R
t
S
2
R
R
m
qB
, t T , S 2 R, T
2 R
2 m 2 m
qB
qB