Similar presentations:
Магнитное поле
1.
12. МАГНИТНОЕ ПОЛЕ
• 1. Магнитостатика• 2. Электромагнетизм
Магнитное поле, в отличие от
электрического поля, оказывает силовое
действие только на движущиеся заряды
(токи).
2
3. Магнитостатика
34.
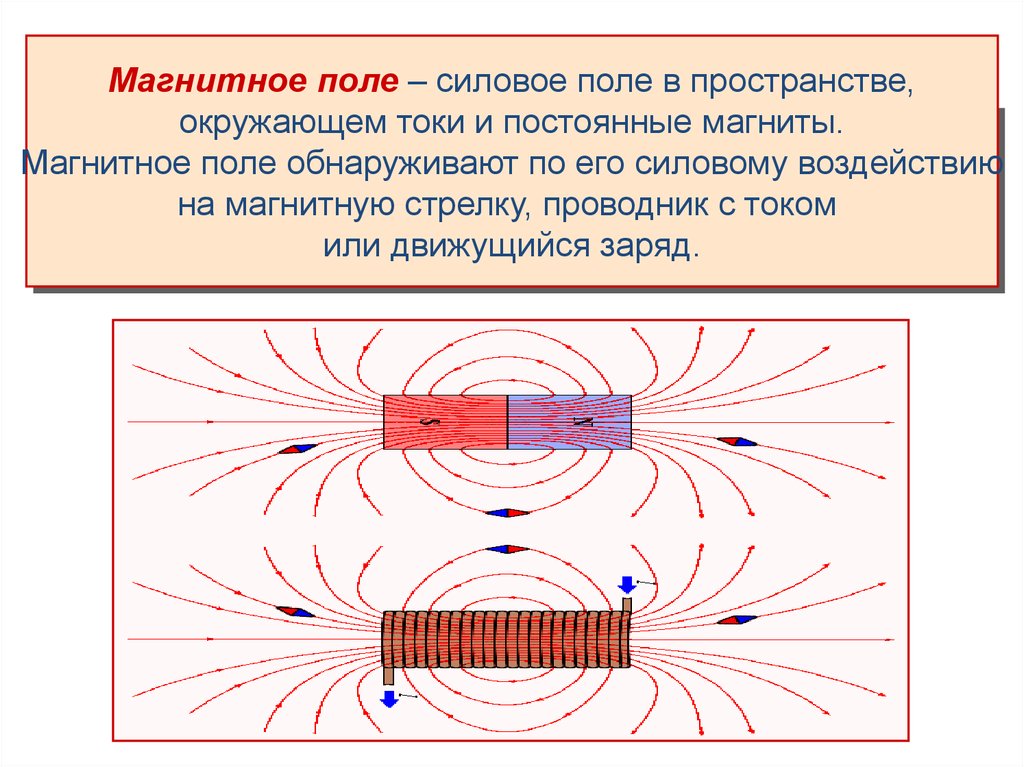
Магнитное поле – силовое поле в пространстве,окружающем токи и постоянные магниты.
Магнитное поле обнаруживают по его силовому воздействию
на магнитную стрелку, проводник с током
или движущийся заряд.
5. Магнитное поле и его характеристики
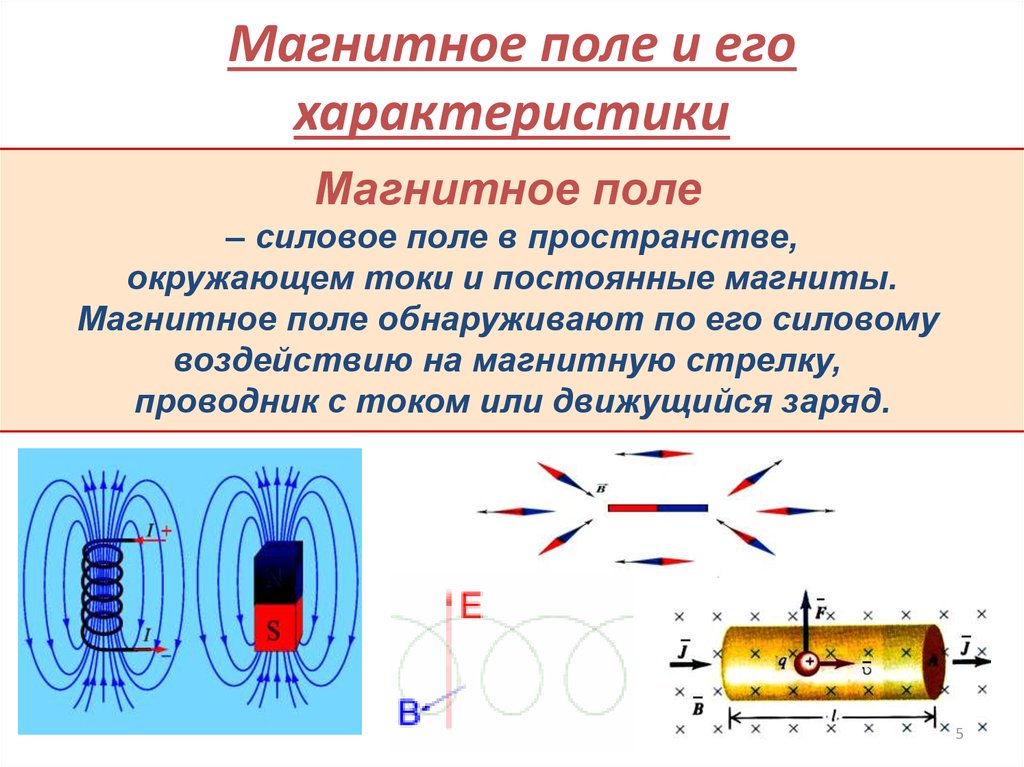
Магнитное поле– силовое поле в пространстве,
окружающем токи и постоянные магниты.
Магнитное поле обнаруживают по его силовому
воздействию на магнитную стрелку,
проводник с током или движущийся заряд.
5
6. ХАРАКТЕРИСТИКИ МАГНИТНОГО ПОЛЯ
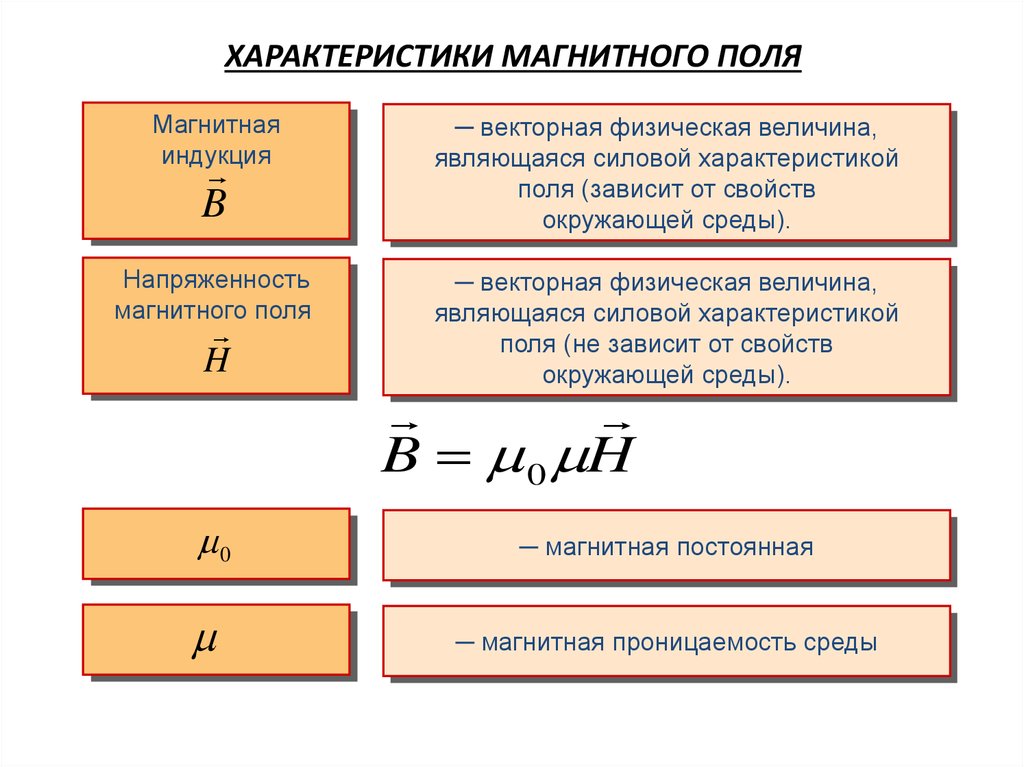
Магнитнаяиндукция
─ векторная физическая величина,
являющаяся силовой характеристикой
поля (зависит от свойств
окружающей среды).
Напряженность
магнитного поля
─ векторная физическая величина,
являющаяся силовой характеристикой
поля (не зависит от свойств
окружающей среды).
B
H
B 0 H
0
─ магнитная постоянная
─ магнитная проницаемость среды
7. Магнитная индукция
Силовой характеристикой магнитного поляявляется вектор магнитной индукции
Вектор магнитной индукции определяет силы,
действующие на токи или движущиеся заряды в
магнитном поле.
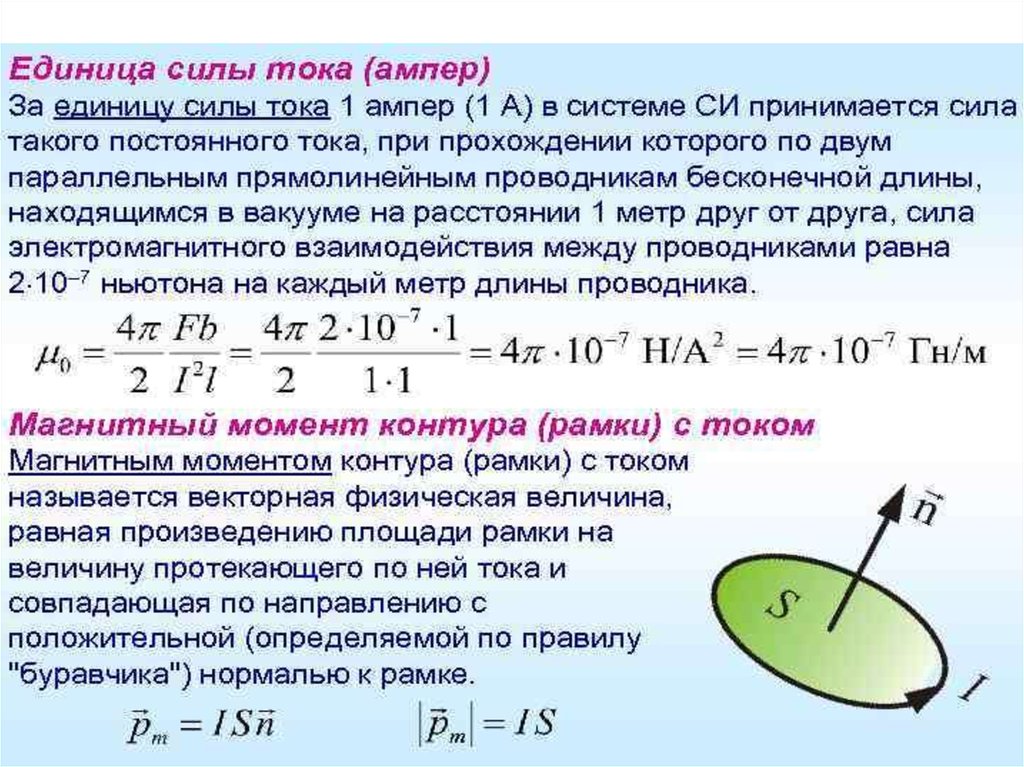
За
положительное
направление
вектора
магнитной индукции принимается направление от
южного полюса S к северному полюсу N магнитной
стрелки,
свободно
устанавливающейся
в
магнитном поле.
8. Кроме вектора магнитной индукции, магнитное поле характеризуется вектором напряженности
где μ0 – магнитная постоянная.B μμ0 H
–7
–6
2
μ0 = 4π·10 г/м ≈ 1,26·10 H/A
Аналогично силовым линиями в электростатике можно
построить линии магнитной индукции.
Магнитное поле изображается линиями магнитной индукции,
т.е. линиями, касательная в каждой точке которых совпадает
с направлением вектора магнитной индукции.
Линии магнитной индукции всегда замкнуты, они нигде не
обрываются. Это означает, что магнитное поле не имеет
источников – магнитных зарядов, которых в природе не
существует . Такие силовые поля- вихревые
8
9. Характеристики магнитного поля (2)
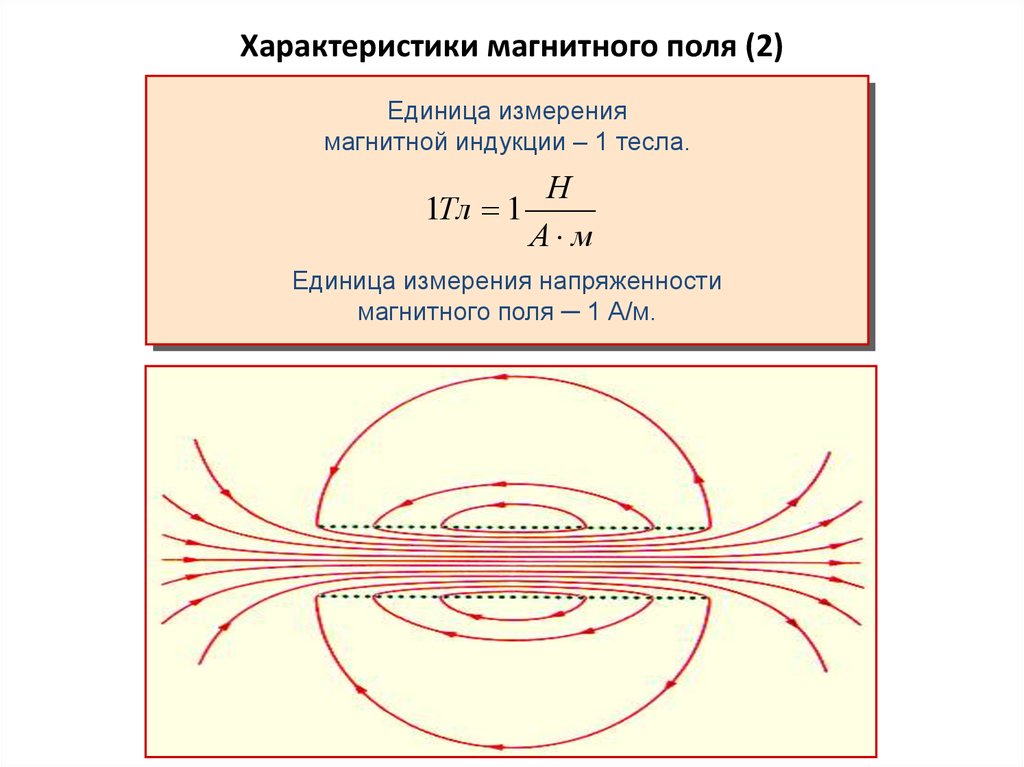
Единица измерениямагнитной индукции – 1 тесла.
1Тл 1
Н
А м
Единица измерения напряженности
магнитного поля ─ 1 А/м.
10.
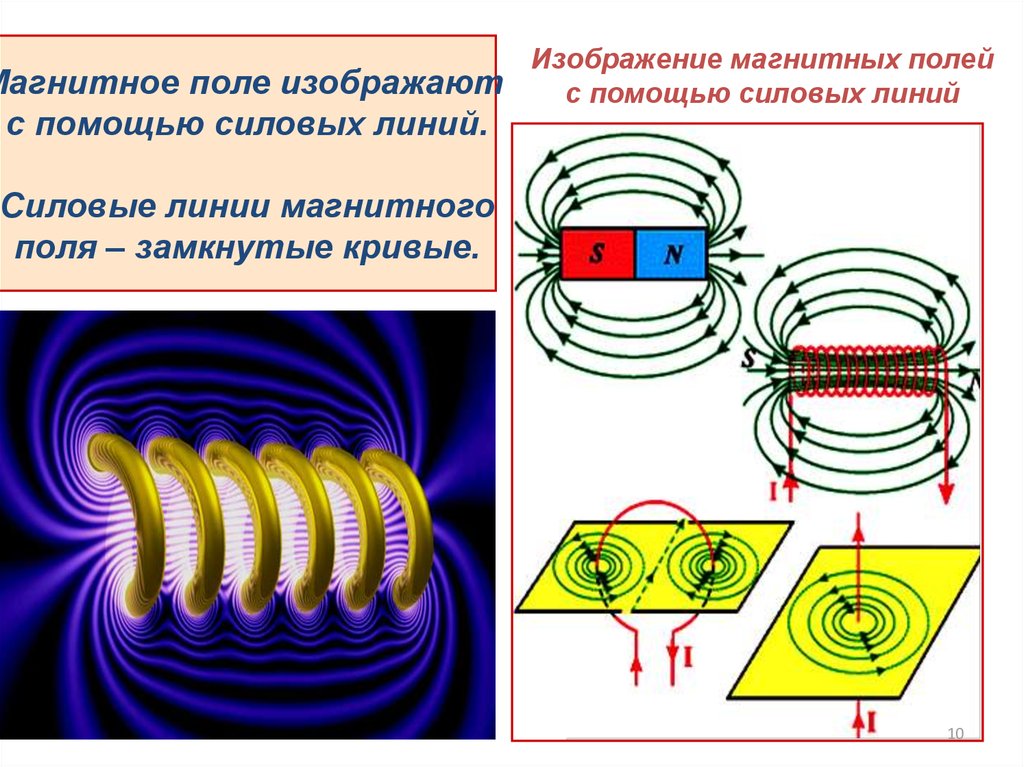
Изображение магнитных полейМагнитное поле изображают
с помощью силовых линий
с помощью силовых линий.
Силовые линии магнитного
поля – замкнутые кривые.
10
11. Направление линий магнитной индукции поля,
• созданного током, определяется поправилу правого винта: если
направление поступательного
движения винта совпадает с
направлением тока, то направление
вращения укажет направление линий
магнитной индукции.
11
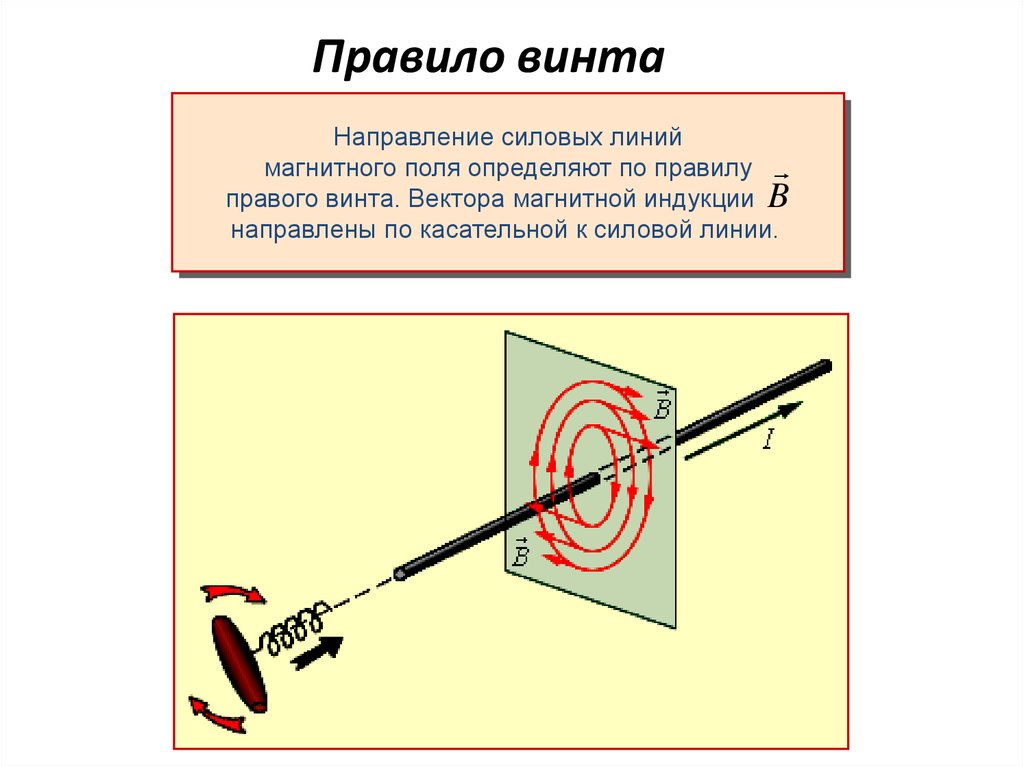
12. Правило винта
Направление силовых линиймагнитного поля определяют по правилу
правого винта. Вектора магнитной индукции B
направлены по касательной к силовой линии.
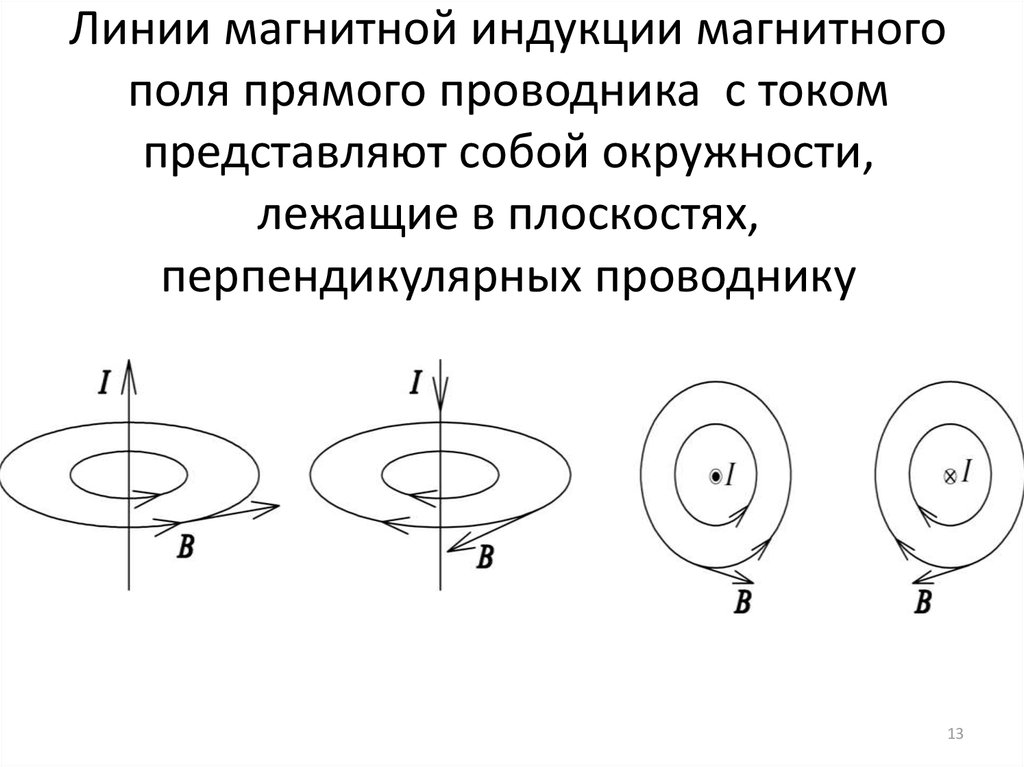
13. Линии магнитной индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях,
перпендикулярных проводнику13
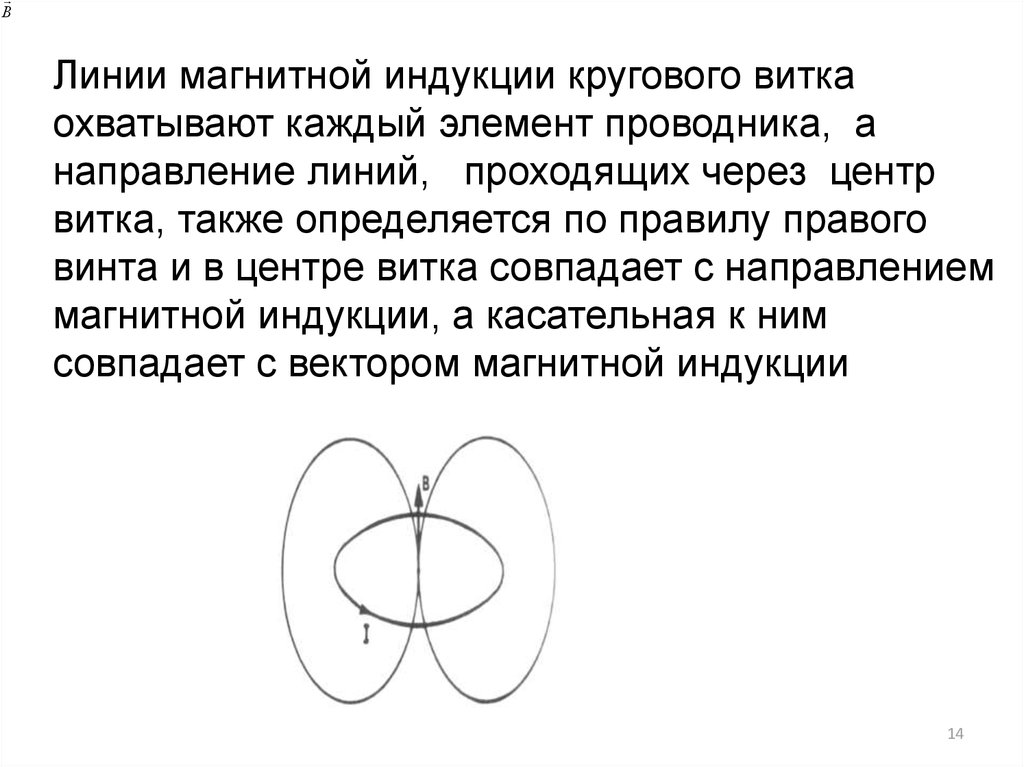
14.
ВЛинии магнитной индукции кругового витка
охватывают каждый элемент проводника, а
направление линий, проходящих через центр
витка, также определяется по правилу правого
винта и в центре витка совпадает с направлением
магнитной индукции, а касательная к ним
совпадает с вектором магнитной индукции
14
15.
Магнитное поле, созданное длинной прямойкатушкой с током (соленоидом) в ее центре
изменяется незначительно, и его можно
считать однородным. Вектор магнитной
индукции входит в соленоид с той стороны, с
которой направление тока в витках катушки
представляется соответствующим ходу часовой
стрелки .Внутри соленоида поле отсутствует
15
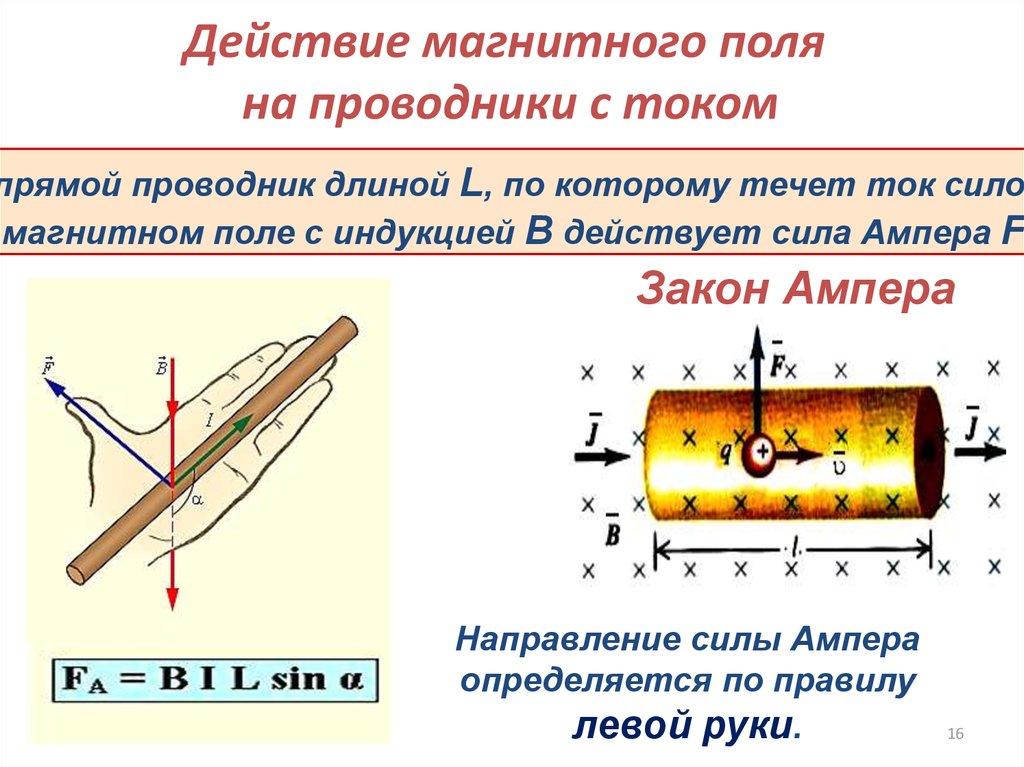
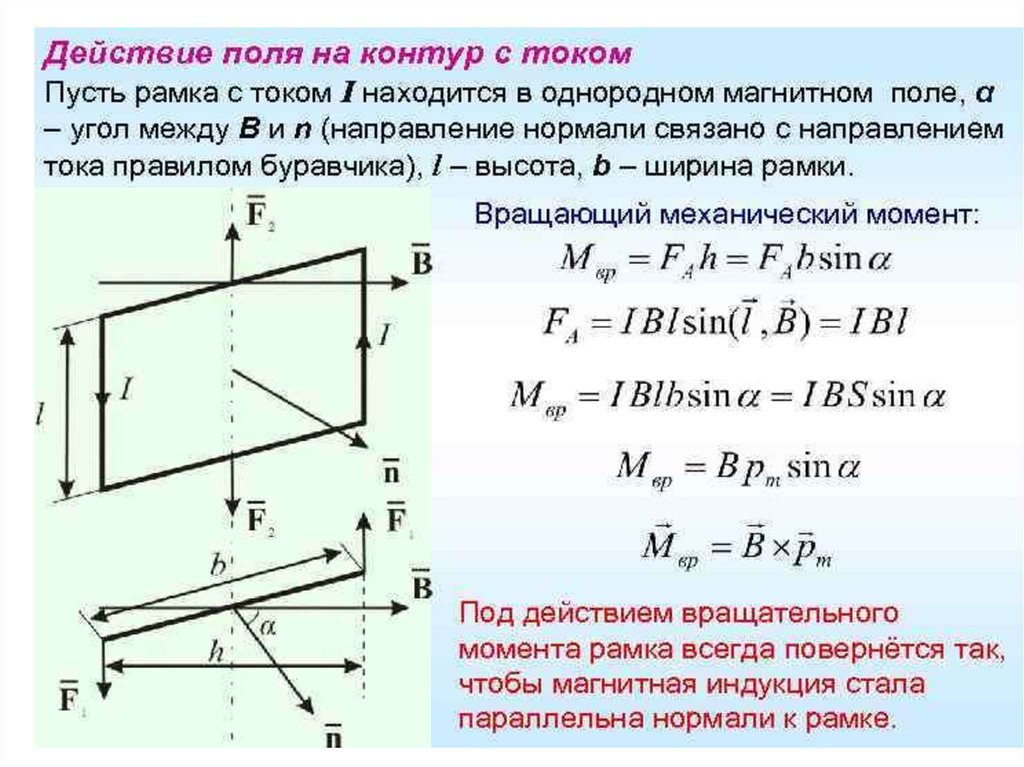
16. Действие магнитного поля на проводники с током
прямой проводник длиной L, по которому течет ток силоймагнитном поле с индукцией В действует сила Ампера FA
Закон Ампера
Направление силы Ампера
определяется по правилу
левой руки.
16
17.
Модуль векторамагнитной индукции
равен отношению
максимального
значения силы
Ампера,
действующей на
прямой проводник с
током, к силе тока I
в проводнике и его
длине Δl:
В системе единиц СИ
за единицу магнитной
индукции принята
индукция такого
магнитного поля, в
котором на каждый
метр длины
проводника при силе
тока 1 А действует
максимальная сила
Ампера 1 Н. Эта
единица называется
тесла (Тл).
17
18.
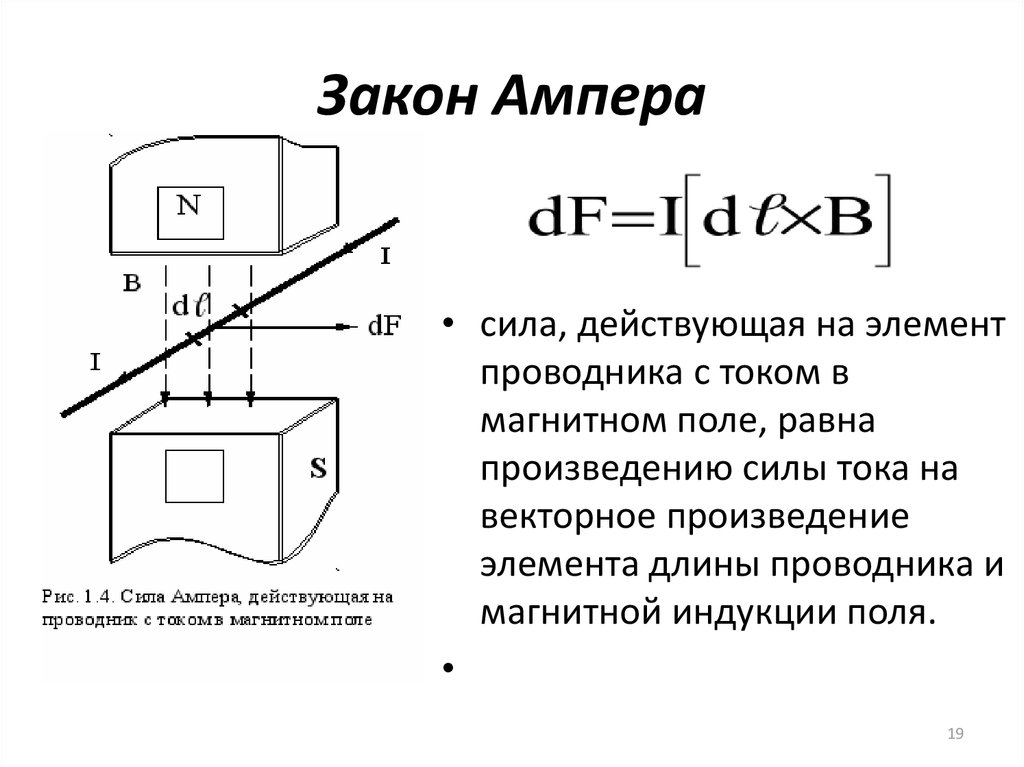
1819. Закон Ампера
• сила, действующая на элементпроводника с током в
магнитном поле, равна
произведению силы тока на
векторное произведение
элемента длины проводника и
магнитной индукции поля.
19
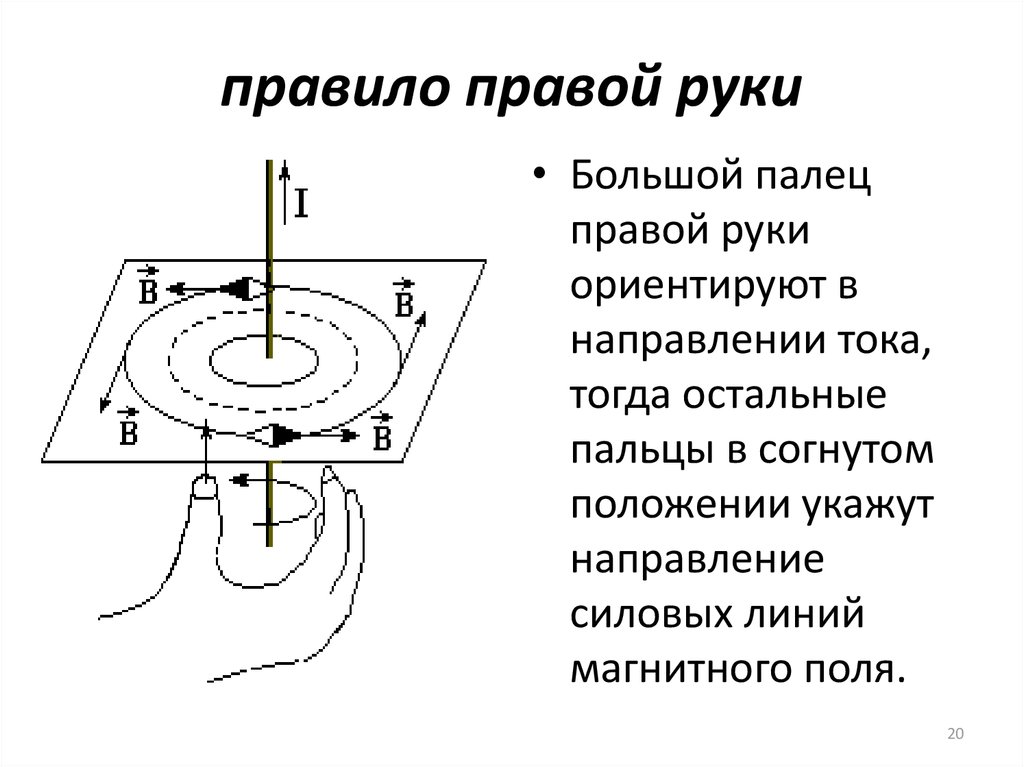
20. правило правой руки
• Большой палецправой руки
ориентируют в
направлении тока,
тогда остальные
пальцы в согнутом
положении укажут
направление
силовых линий
магнитного поля.
20
21.
2122.
2223.
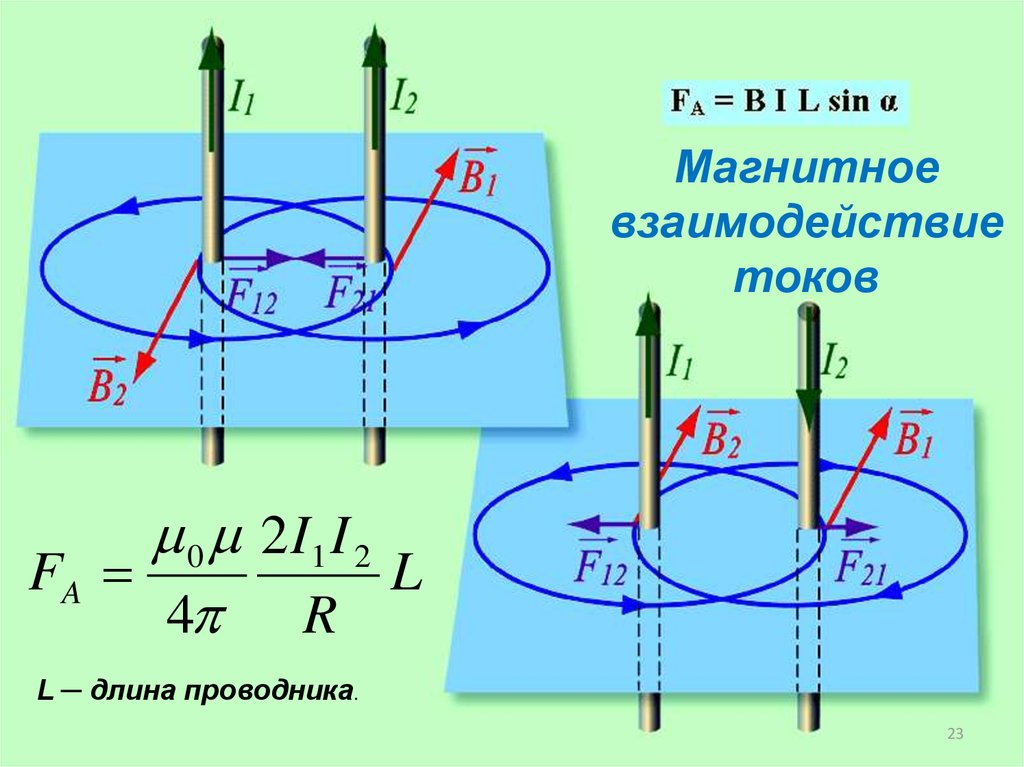
Магнитноевзаимодействие
токов
0 2I1 I 2
FA
L
4 R
L ─ длина проводника.
23
24.
2425.
2526.
2627. Действие магнитного поля на рамку с током широко применяется в электроизмерительных приборах.
• Работа любого прибора магнитоэлектрическойсистемы основана на взаимодействии
магнитного поля постоянного магнита и рамки с
током. Возникает вращающий момент, который
будет поворачивать рамку. Угол поворота рамки
и связанные с ним показания шкалы прибора
будут зависеть от силы тока в рамке.
27
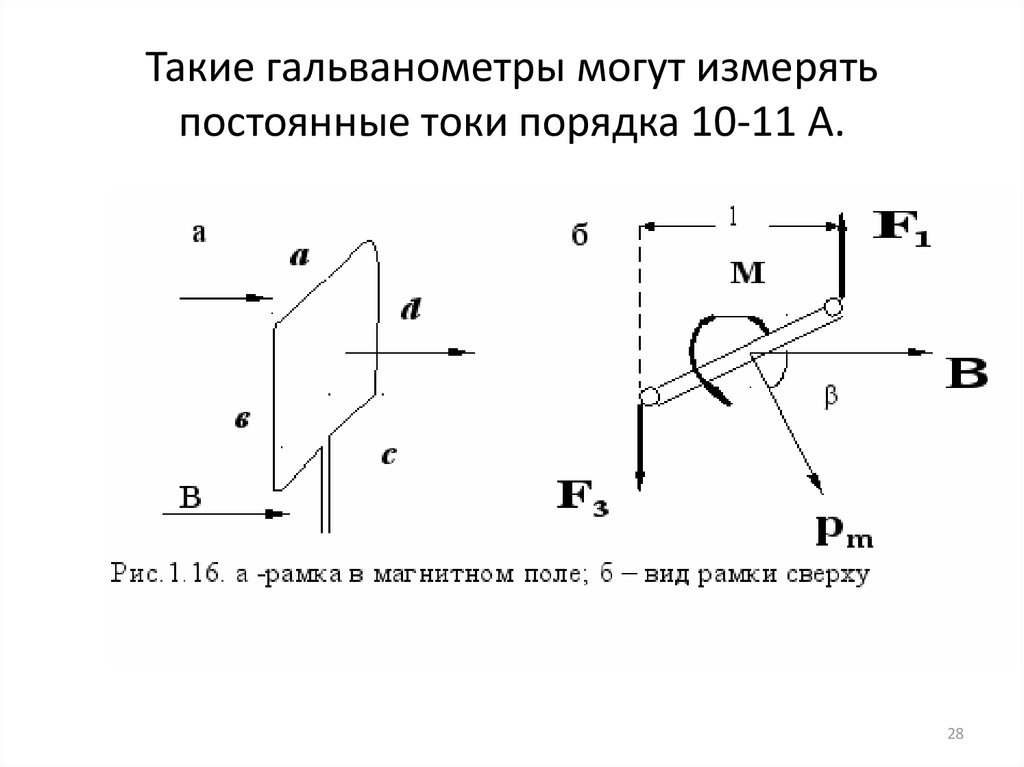
28. Такие гальванометры могут измерять постоянные токи порядка 10-11 А.
Такие гальванометры могут измерятьпостоянные токи порядка 10-11 А.
28
29.
Действие магнитного поляна
движущиеся заряды.
29
30.
Bажнейшая особенность магнитного полясостоит в том, что оно действует только на
движущиеся электрические заряды. В результате
опытов было установлено, что любая
заряженная частица, движущаяся в магнитном
поле, испытывает действие силы F, которая
пропорциональна величине магнитного поля в
этой точке. Направление этой силы всегда
перпендикулярно скорости движения частицы и
зависит от угла между направлениями v и B.
30
31. . Движение зарядов в магнитных полях
Считаем, что магнитное поле однородно и на частицуне действуют электрические поля. Рассмотрим три
возможных случая:
1)
Заряженная частица движется в магнитном
поле вдоль линий магнитной индукции
2) Заряженная частица движется в магнитном
поле со скоростью
• 3) Заряженная частица движется под углом к
• линиям магнитной индукции .
31
32. 1. Магнитное поле не действует на заряженную частицу в двух случаях : если частица неподвижна ( V=0) или если частица ( V и B
–параллельны) (движется вдольсиловой линии магнитного поля.
2. Если вектор скорости перпендикулярен , то
сила Лоренца создает центростремительное
ускорение и частица будет двигаться по
окружности.
3. Если скорость направлена под углом к , то
заряженная частица движется по спирали,
ось которой параллельна магнитному полю.
32
33.
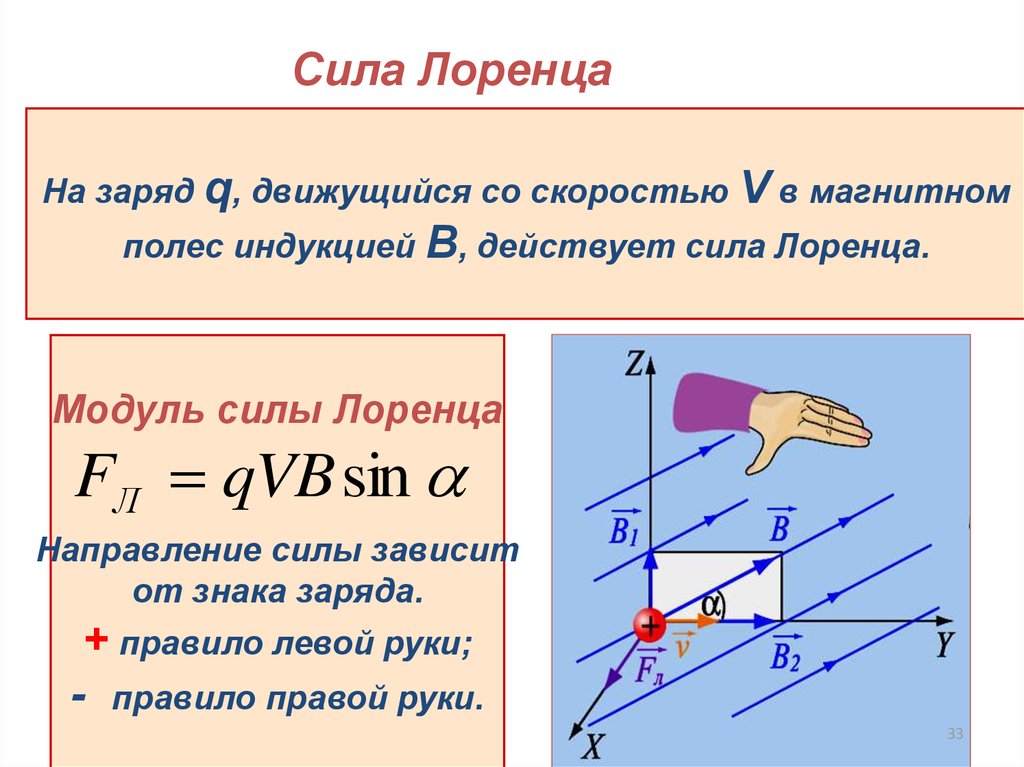
Сила ЛоренцаНа заряд q, движущийся со скоростью V в магнитном
полес индукцией B, действует сила Лоренца.
Модуль силы Лоренца
FЛ qVB sin
Направление силы зависит
от знака заряда.
+ правило левой руки;
- правило правой руки.
33
34.
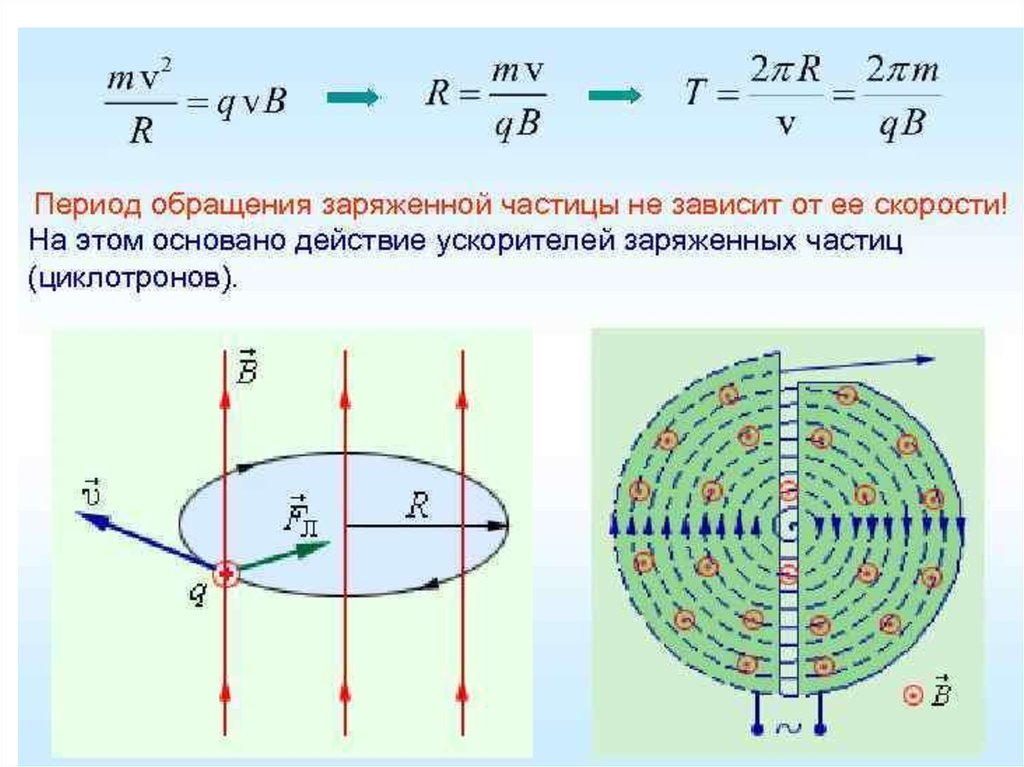
0 sin 0 FЛ 02
sin 1 FЛ qVB
Движение по окружности
радиуса R.
Радиус окружности
определяется из условия
mV 2
mV
qVB
R
R
qB
Период вращения частицы
2 m
T
B q
34
35.
3536.
3637.
Направление силы Лоренца определяется поправилу левой руки:
Если ладонь левой руки расположить так, в нее
входил вектор магнитной индукции, а четыре
вытянутых пальца направить вдоль вектора
, то
отогнутый большой палец укажет направление силы,
действующей на положительный заряд. Сила
Лоренца перпендикулярна векторам
и
. При
движении частицы в магнитном поле сила Лоренца
37
не совершает работы и ее Wk не меняется.
38.
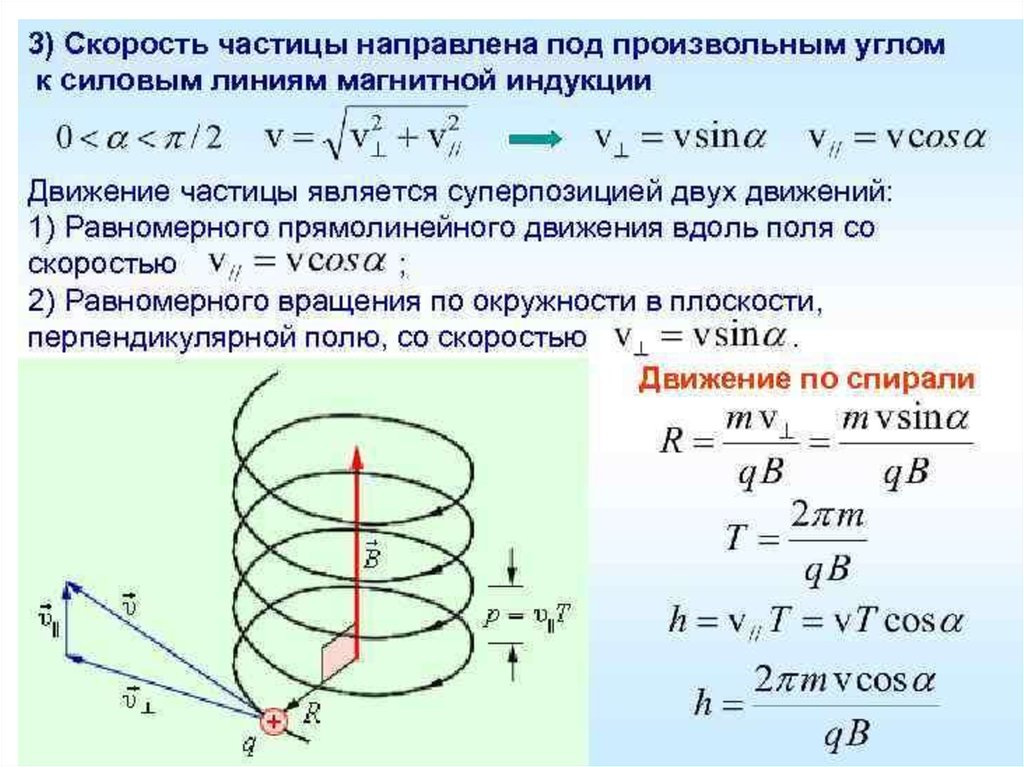
Движение частицы под углом к направлениювектора магнитной индукции
Состоит из двух движений:
1) равномерное движение по окружности;
2) равномерное прямолинейное движение вдоль поля.
В результате сложения двух движений
возникает движение по винтовой линии.
38
39.
3940.
4041.
4142.
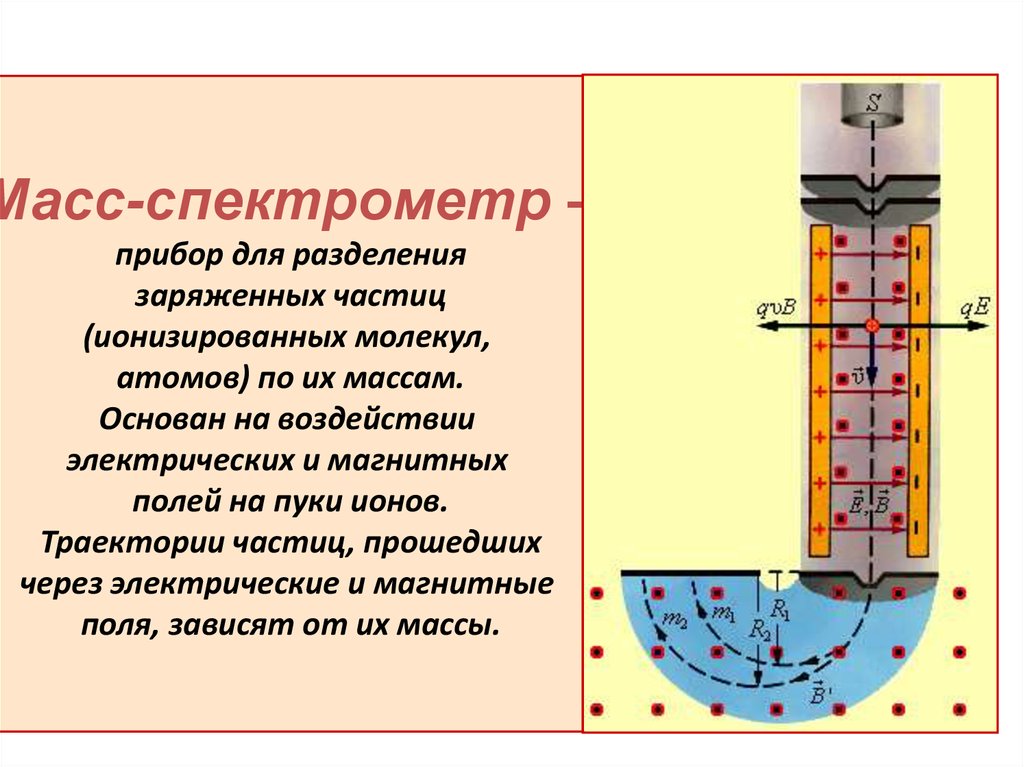
Масс-спектрометр –прибор для разделения
заряженных частиц
(ионизированных молекул,
атомов) по их массам.
Основан на воздействии
электрических и магнитных
полей на пуки ионов.
Траектории частиц, прошедших
через электрические и магнитные
поля, зависят от их массы.
43. Кроме магнитной силы, на заряд может действовать также и электрическая сила и результирующая электромагнитная сила, действующая
на заряд, имеетвид
43
44.
Магнитное поле Земли, образующее земнуюмагнитосферу, простирается на расстоянии 70
– 80 тысяч км в направлении к Солнцу и на
многие миллионы километров в обратном
направлении. В околоземном пространстве
магнитное поле образует магнитную ловушку
для заряженных частиц высоких энергий.
Происхождение магнитного поля Земли
связывают с движениями проводящего жидкого
вещества в земном ядре
Из других планет Солнечной системы лишь
Юпитер и Сатурн обладают заметными
магнитными полями.
Магнитное поле Солнца играет важнейшую
роль во всех происходящих на Солнце процессах44
45. Магнитное поле Земли
4546.
4647.
Проходя через верхниеслои атмосферы, поток
заряженных частиц
вызывает появление
свечения.
Поэтому в полярных
широтах часто
наблюдается такое
явление, как
«полярное сияние».
47
48.
Действие магнитного поля Земли вблизиземной поверхности изменяет траекторию
движения частиц, испускаемых Солнцем и
звездами. Этим объясняется так называемый
широтный эффект, заключающийся в том, что
интенсивность космических лучей, доходящих
до Земли, вблизи экватора меньше, чем в
более высоких широтах. Действием магнитного
поля Земли объясняется тот факт, что
полярное сияние наблюдается только в самых
высоких широтах, на Крайнем Севере. Именно
в том направлении магнитное поле Земли
отклоняет заряженные космические частицы,
которые вызывают свечение атмосферы,
48
называемое полярным сиянием.
49.
4950.
5051.
5152.
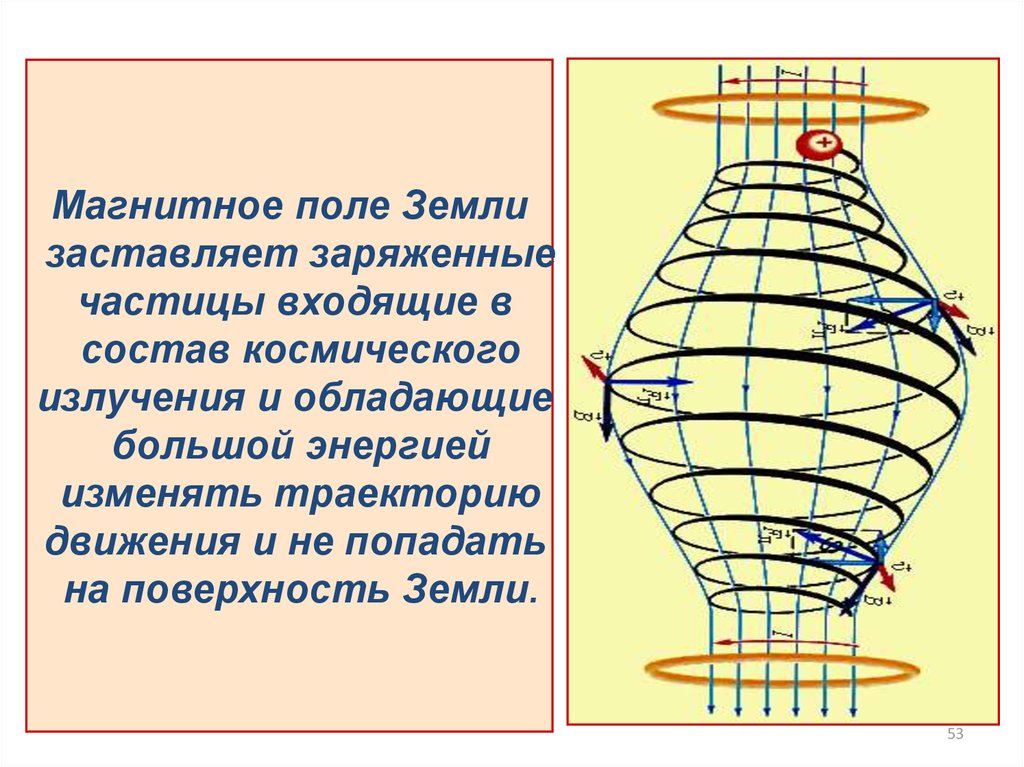
5253.
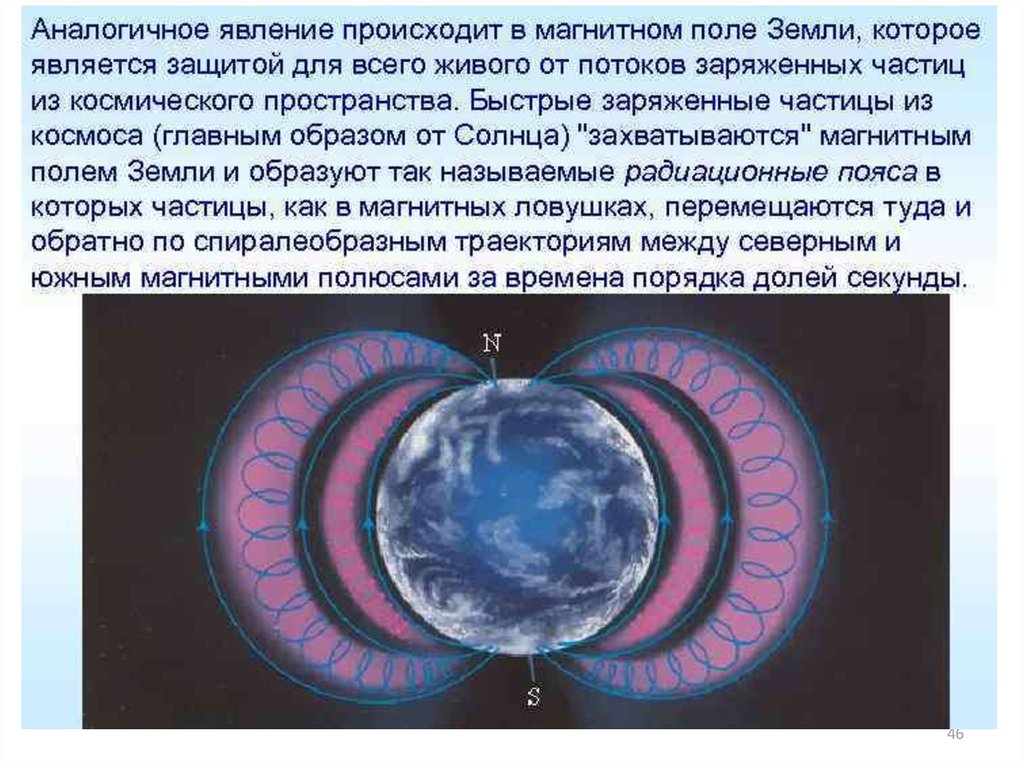
Магнитное поле Землизаставляет заряженные
частицы входящие в
состав космического
излучения и обладающие
большой энергией
изменять траекторию
движения и не попадать
на поверхность Земли.
53
54. Закон Био–Савара-Лапласа
• Французские физики Ф. Савар и Ж.Б. Биоизучали магнитное поле, создаваемое
проводниками с постоянным током
различной формы. На основании
многочисленных опытов они пришли к
выводу, что магнитная индукция поля
проводника с током пропорциональна силе
тока I, зависит от формы и размеров
проводника, а также от расположения
рассматриваемой точки по отношению к
проводнику.
54
55.
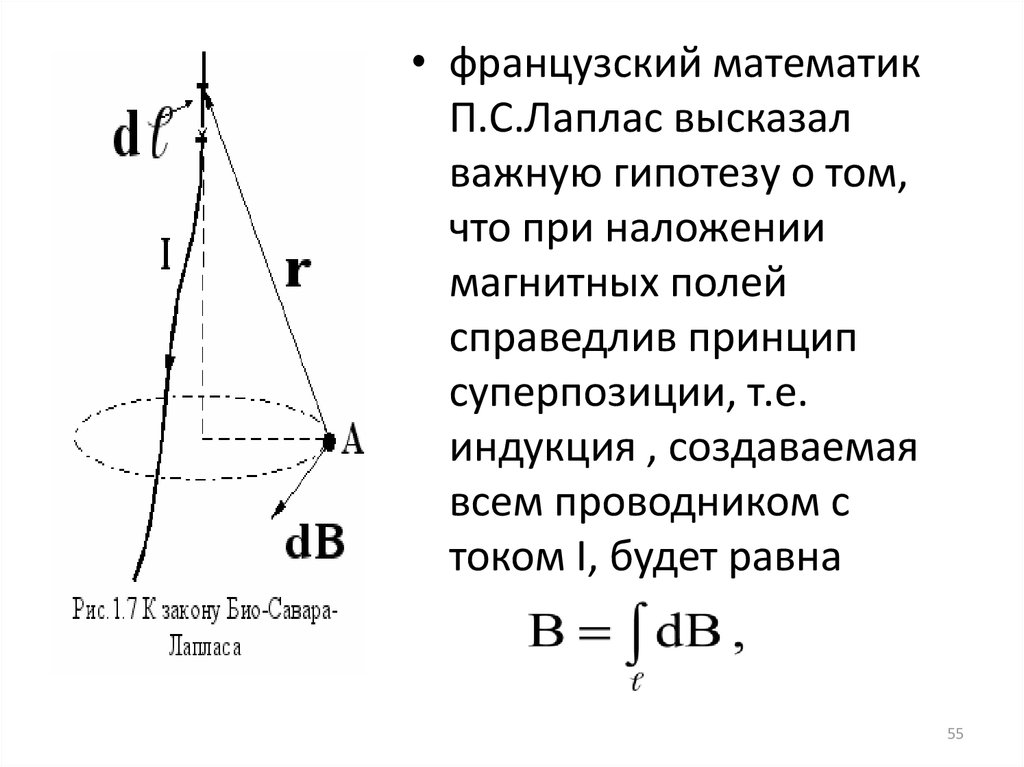
• французский математикП.С.Лаплас высказал
важную гипотезу о том,
что при наложении
магнитных полей
справедлив принцип
суперпозиции, т.е.
индукция , создаваемая
всем проводником с
током I, будет равна
55
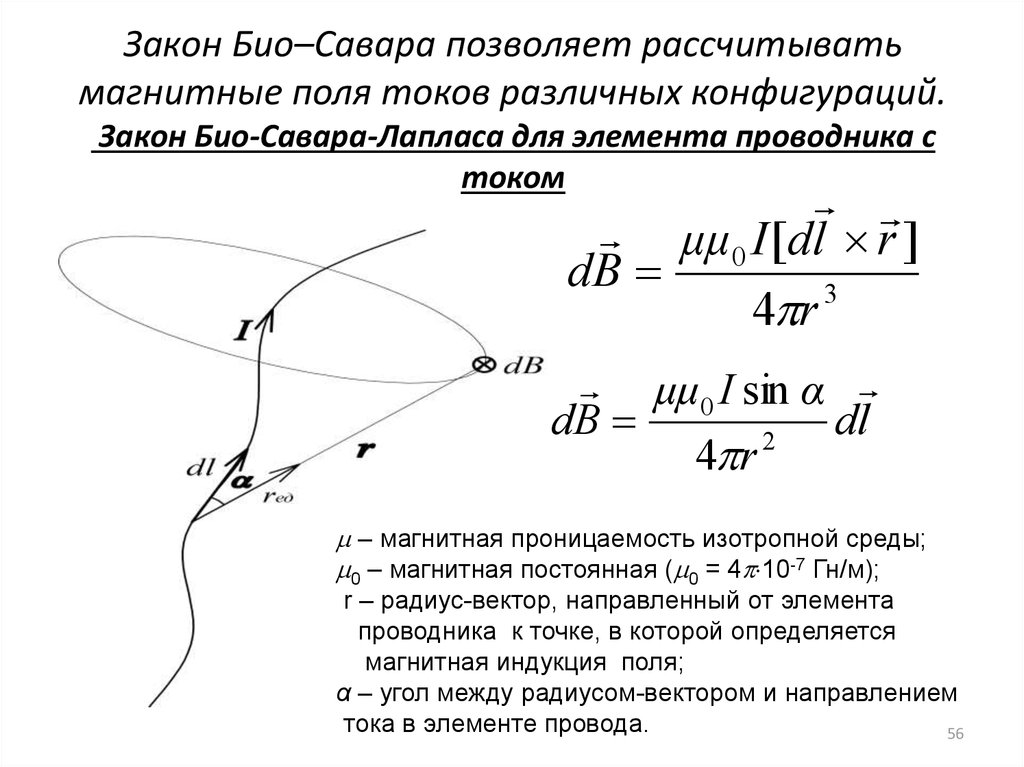
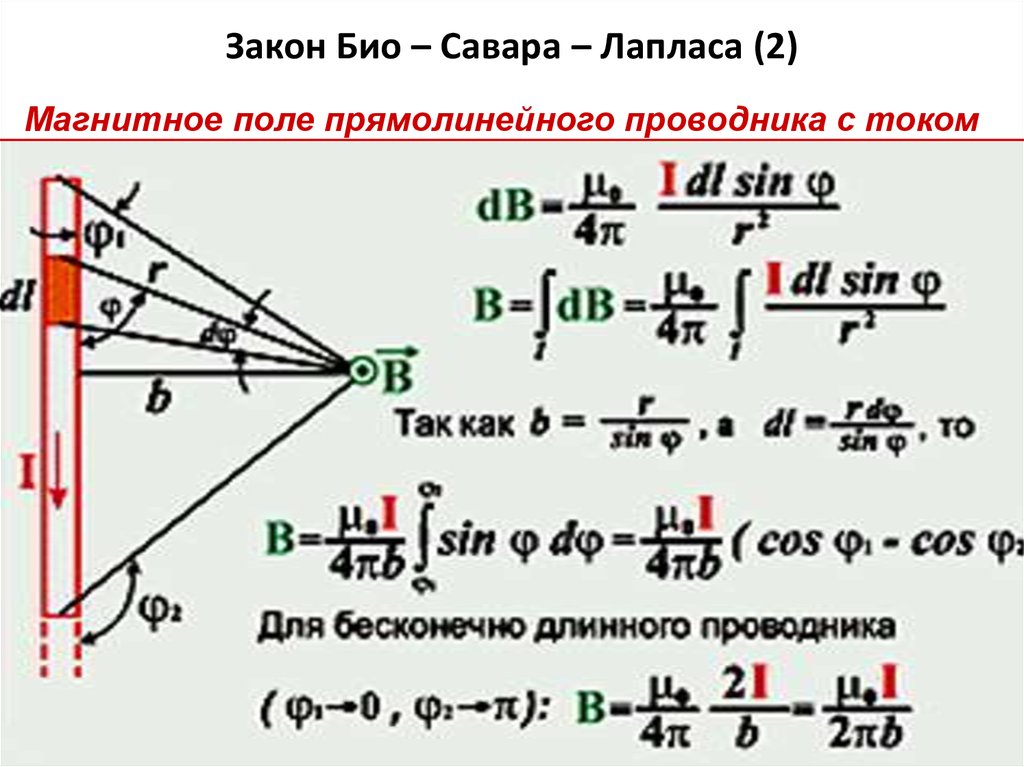
56. Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Закон Био-Савара-Лапласа для элемента
проводника стоком
μμ0 I [dl r ]
dB
3
4 r
μμ0 I sin α
dB
dl
2
4 r
– магнитная проницаемость изотропной среды;
0 – магнитная постоянная ( 0 = 4 10-7 Гн/м);
r – радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция поля;
α – угол между радиусом-вектором и направлением
тока в элементе провода.
56
57.
Магнитная индукция поля1) созданного бесконечно длинным прямым
проводником с током (рис.1) ,
μμ0 I
B
2 r0
(рис.1)
(рис.2)
2). в центре кругового витка с током ( рис.2) (h=r)
μμ 0 I
B
2R
B
μμ0 IR 2
2( R 2 h 2 )
3
2
57
58.
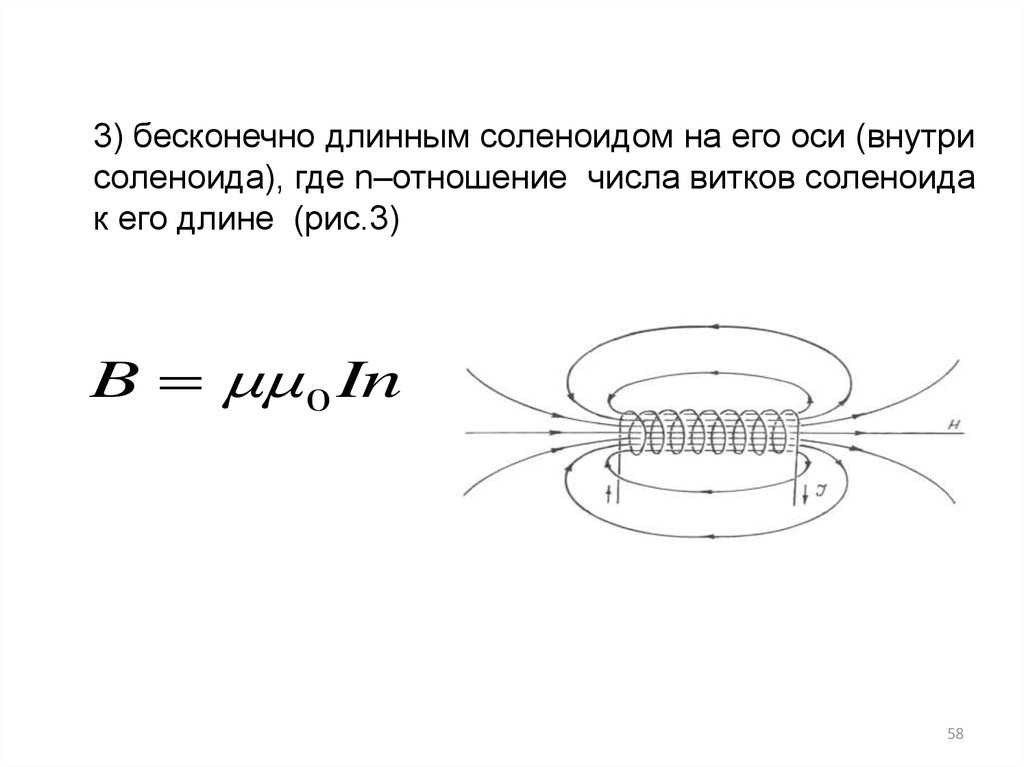
3) бесконечно длинным соленоидом на его оси (внутрисоленоида), где n–отношение числа витков соленоида
к его длине (рис.3)
B μμ0 In
58
59. Закон Био – Савара – Лапласа (2)
Магнитное поле прямолинейного проводника с током60. Магнитное поле кругового тока
B dBl
Магнитное поле кругового
тока
y
B
dBy
dB
A
dBx
r
O
R
I
dl
x
• Выделим на кольце
элемент проводника dl
с током I и от него в
точку А проведем
радиус-вектор r
(рисунок). Вектор dB
магнитной индукции
Idl поля, создаваемого
элементом тока Idl в
точке А, направим в
соответствии с
правилом буравчика. 60
61. Согласно принципу суперпозиции магнитных полей, магнитная индукция В в точке А определяется интегрированием , где
dBСогласно принципу суперпозиции магнитных полей,
магнитная индукция В в точке А определяется
интегрированием B dB , где интегрирование
l
ведется по всем элементам
dl кольца.
• Разложим вектор dB на две составляющие:
параллельную плоскости кольца и перпендикулярную
т. е.
плоскости кольца,
B dBx dB y
• dB dBx dBy
, тогда
l
l
В силу симметрии
l dB.x 0 Векторы от
различных элементов dl сонаправлены,
поэтому скалярное значение вектора будет
равно: B dBy , где по закону Био-Савараl
Лапласа
61
62.
dBy dB cos βμμ0 Idl
dB
sin α
2
4 r
• Так как вектор dl перпендикулярен , то sin α =1.
Следовательно,
μμ0 I dl
μμ0 I cos β
B
cosβ
2
2
4
r
4
r
l
2 R
μμ0 I cos β 2 R
0 dl
4 r 2
R
Где cos β
. Тогда получим.
r
R
μμ 0 I
2 R
2
μμ
IR
0
r
B
4 r 2
2r 3
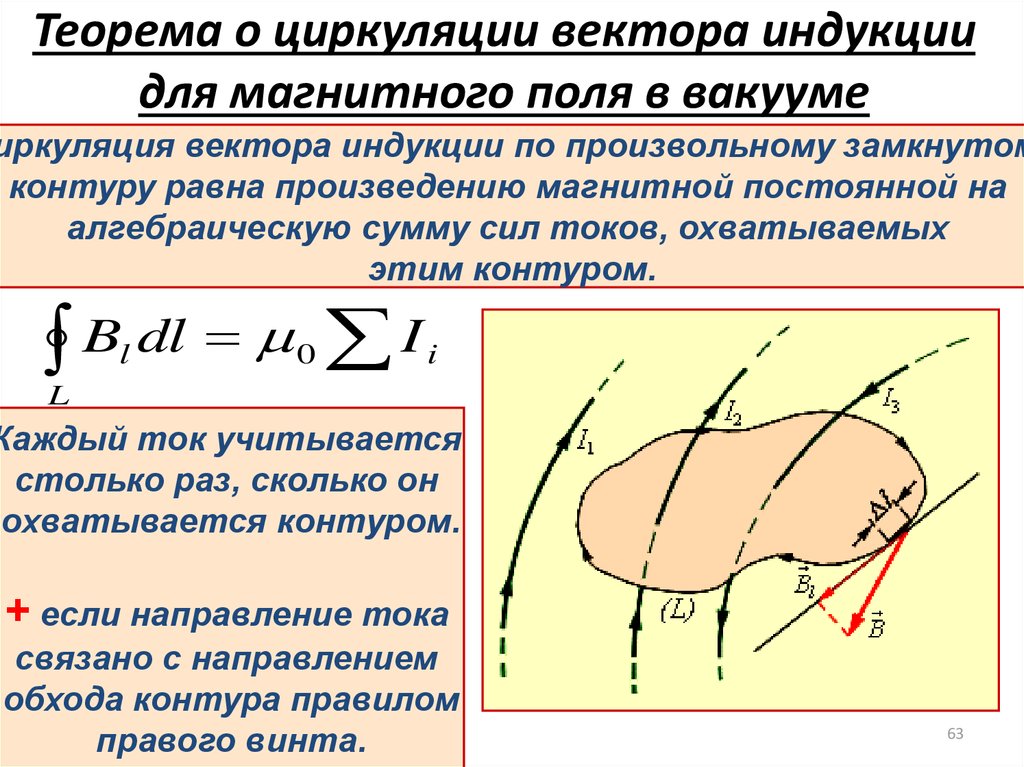
63. Теорема о циркуляции вектора индукции для магнитного поля в вакууме
иркуляция вектора индукции по произвольному замкнутомконтуру равна произведению магнитной постоянной на
алгебраическую сумму сил токов, охватываемых
этим контуром.
B dl I
l
0
i
L
Каждый ток учитывается
столько раз, сколько он
охватывается контуром.
+ если направление тока
связано с направлением
обхода контура правилом
правого винта.
63
64. Теорема о циркуляции вектора магнитной индукции ( Закон полного тока)
• Наряду с законом Био-Савара-Лапласа, длярасчета магнитных полей
используется закон полного тока.
• Циркуляцией вектора В (или Н ) по
произвольному замкнутому контуру
l называется интеграл
64
65. Т.к. угол между векторами В и dl равен нулю, то cos( В, dl)=1. Из полученного результата следует, что циркуляция вектора
магнитной индукции вдоль силовойлинии прямолинейного проводника с током не равна
нулю, т.е. поле такого проводника –вихревое.
Полученная формула справедлива для любой формы
замкнутого контура, охватывающего проводник с током.
• Пусть теперь наш контур ℓ произвольной формы
охватывает n проводников с токами I1, …In. Каждый
ток учитывается столько раз, сколько раз он
охватывается контуром. При этом ток считают
положительным, если он с направлением обхода
контура образует правовинтовую систему. Ток
противоположного направления -отрицательный.
65
66.
Таким образом,циркуляция вектора В по
произвольному
замкнутому контуру
равна произведению
магнитной постоянной
на алгебраическую сумму
токов, охватываемых
этим контуром:
66
67. Данное выражение представляет собой закон полного тока для магнитного поля в вакууме, или теорему о циркуляции вектора В.
Циркуляция вектора В (или Н) попроизвольному замкнутому контуру прямо
пропорциональна алгебраической сумме
токов, охватываемых этим контуром:
67
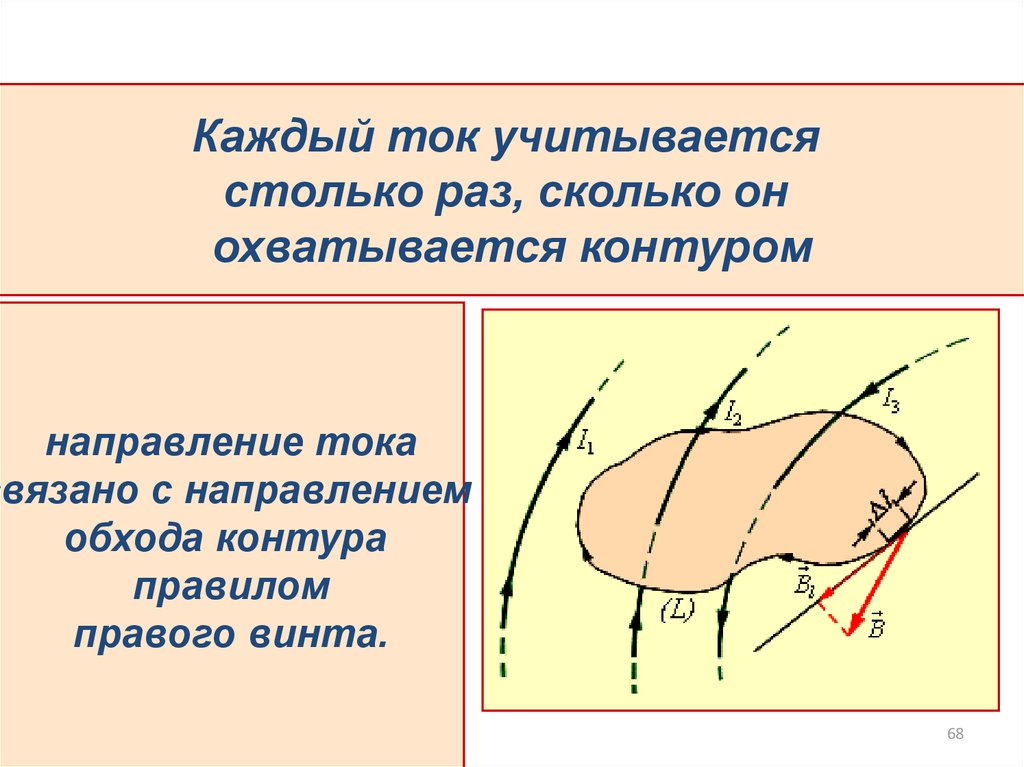
68.
Каждый ток учитываетсястолько раз, сколько он
охватывается контуром
направление тока
связано с направлением
обхода контура
правилом
правого винта.
68
69. Чтобы расчитать магнитное поле нужно:
• 1. выбрать удобный замкнутый контур• 2. вычислить
• 3. вычислить через замкнутый контур
сумму токов.
• 4. приравнять (2) и (3) и найти В.
69
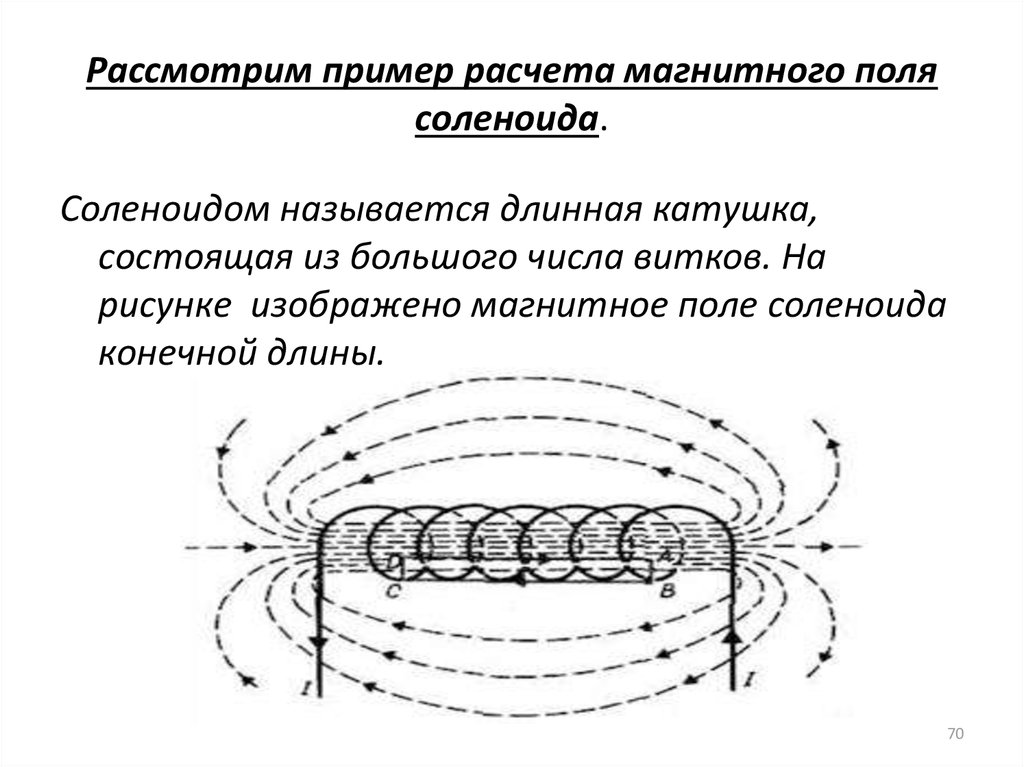
70. Рассмотрим пример расчета магнитного поля соленоида.
Соленоидом называется длинная катушка,состоящая из большого числа витков. На
рисунке изображено магнитное поле соленоида
конечной длины.
70
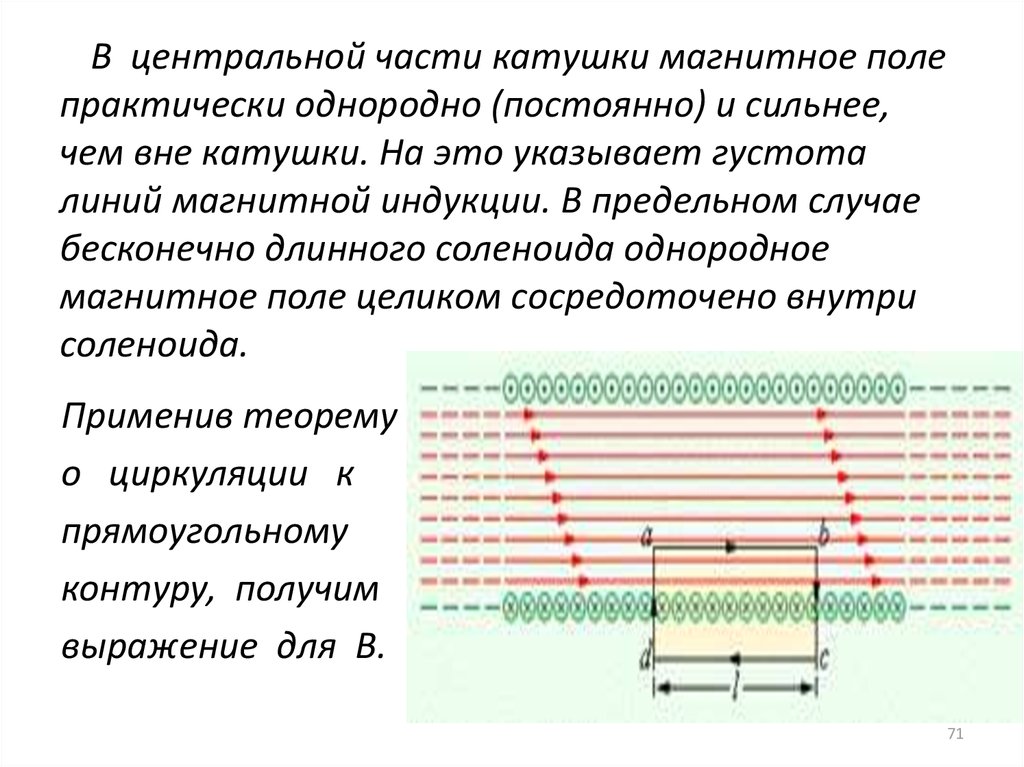
71. В центральной части катушки магнитное поле практически однородно (постоянно) и сильнее, чем вне катушки. На это указывает
густоталиний магнитной индукции. В предельном случае
бесконечно длинного соленоида однородное
магнитное поле целиком сосредоточено внутри
соленоида.
Применив теорему
о циркуляции к
прямоугольному
контуру, получим
выражение для В.
71
72. : Вектор В отличен от нуля только вдоль стороны ab замкнутого контура abcd, используя закон полного тока, получим , где n=N/l
: dl B dl B dl nIB
dl
B
dl
B
dl
B
l l l l l l 0
L
ab
bc
cd
da
ab
Вектор В отличен от нуля только вдоль
стороны ab замкнутого контура abcd, используя
закон полного тока, получим
,
где n=N/l – число витков
соленоида на единицу длины
72
73. Теорема Остроградского-Гаусса для магнитного поля
• Поток магнитного поля через любуюзамкнутую поверхность равен нулю.
• Эта теорема отражает факт отсутствия
магнитных зарядов, вследствие чего линии
магнитной индукции не имеют ни начала,
ни конца и являются замкнутыми.
73
74.
Поток векторамагнитной индукции
Потоком вектора магнитной индукции
через элементарную площадку dS
называется физическая величина dФm,
равная произведению величины этой
площадки и проекции вектора В на
направление нормали к площадке dS
74
75.
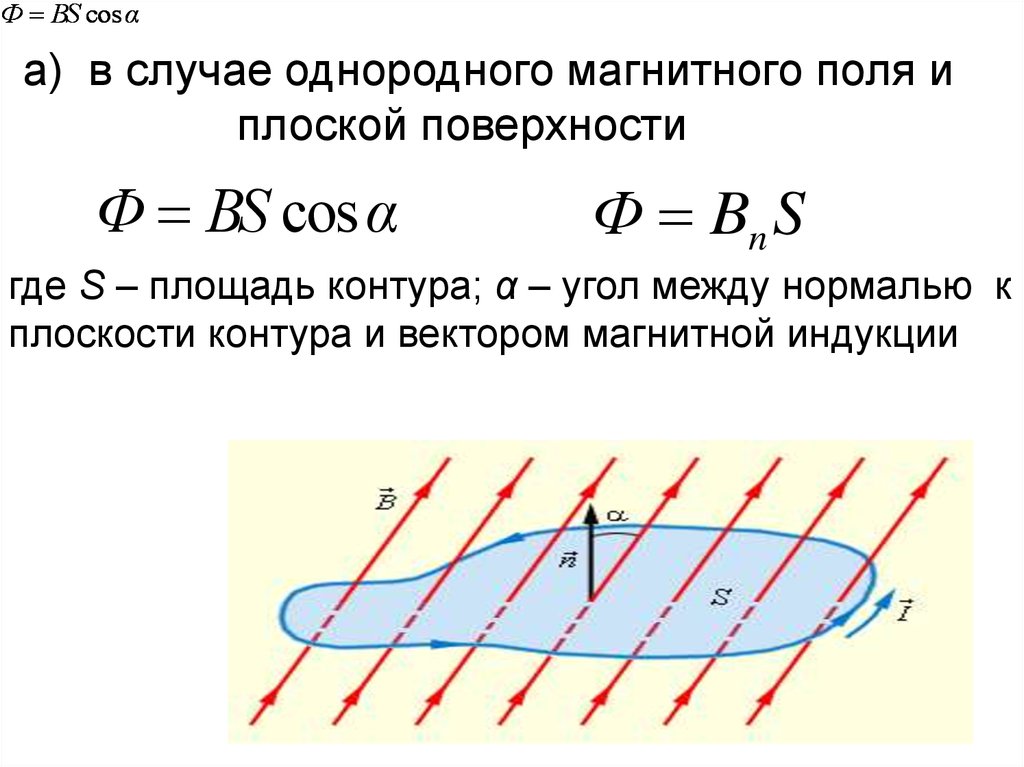
Ф BS cos αа) в случае однородного магнитного поля и
плоской поверхности
Ф BS cos α
Ф Bn S
где S – площадь контура; α – угол между нормалью к
плоскости контура и вектором магнитной индукции
75
76. б) неоднородного магнитного поля и произвольной поверхности
• Интегрируя это выражение по S, получиммагнитный поток Фm сквозь произвольную
поверхность S:
Вn =Bcos α
76
77. Механическая работа в магнитном поле
7778. A=JФ
A=J Ф• Работа силы Ампера при перемещении проводника
конечной длины с постоянным током равна
произведению тока на изменение потока магнитной
индукции через площадь контура , очерченную
проводником при его движении в магнитном поле .
• Если работу совершают силы поля, то А 0 и энергия
поля убывает.
• Сила Лоренца не совершает работу. Под действием
силы Лоренца меняется только направление
скорости заряда
78
79. Запишем уравнения системы уравнений Максвелла для магнитостатики
• 1.- в природе отсутствуют
магнитные заряды
• 2.
- источником
магнитного поля является электрический
ток.
79

















































 physics
physics








