Similar presentations:
Электромагнитное поле. Лекция 5
1. ЛЕКЦИЯ 5
2.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ3.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ–физическое поле посредством которого
осуществляется взаимодействие электрически
заряженных частиц и частиц обладающих
магнитным моментом. Условно делится на
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ и МАГНИТНОЕ ПОЛЕ
4. МАГНИТНОЕ ПОЛЕ
5. МАГНИТНОЕ ПОЛЕ И ЕГО ХАРАКТЕРИСТИКИ
6. МАГНИТНОЕ ПОЛЕ
• МАГНИТНОЕ ПОЛЕ – одна из форм проявления электромагнитного поля, отличающаяся только тем, чтодействует только на движущиеся электрически заряженые частицы и тела, на проводники с током и тела
обладающие магнитным моментом.
• МАГНИТНОЕ ПОЛЕ создается проводниками с током,
движущимися электрически заряженными частицами
и телами с магнитным моментом отличным от нуля.
• МАГНИТНОЕ ПОЛЕ имеет количественные характеристики : МАГНИТНУЮ ИНДУКЦИЮ и НАПРЯЖЕННОСТЬ
МАГНИТНОГО ПОЛЯ
7.
• Все постоянные магниты имеют два разноименных полюса: северный и южный.• Одноименные полюса взаимно отталкиваются, а N
разноименные взаимно притягиваются.
• Существует магнитное поле Земли, обусловленS
ное, в основном, процессами происходящими в
жидком ядре Земли. Магнитные полюса Земли
не совпадают с географическими (северный магнитный находится около южного географического), угол между осью вращения Земли и линией 11,5°
Sм
соединяющей магнитные полюса 11,5°.
Nг
Sг
Nм
8.
Магнитное поле не действует на неподвижные электрические заряженные тела, но и эти частицы (тела) недействуют на помещенную около них магнитную
стрелку, то есть не создают магнитного поля.
При пропускании по проводнику постоянного тока, находящаяся под ним магнитная стрелка вращалась вокруг
своей оси, стараясь расположиться перпендикулярно
проводнику. Ось стрелки тем точнее перпендикулярна,
чем больше сила тока и слабее влияние Земли. Было
обнаружено, что направление поворота северного полюса стрелки под действием электрического тока изменяется на противоположное, при изменении тока в
проводнике (опыт Эрстеда).
Вывод: при прохождении по проводнику электрического
тока, вокруг проводника возникает магнитное поле.
9. МАГНИТНЫЙ МОМЕНТ
МАГНИТНЫЙ МОМЕНТ – векторная величина,pm
n
характеризующая магнитные свойства тел и
S
частиц тела, для плоского замкнутого электI
рического контура численно равный произведению силы тока I на площадь S ограниченную контуром и направленную перпендикулярно к плоскости,
в соответствии с правилом правого винта. n – единичный вектор нормали к площади контура.
pm ISn
Магнитное поле оказывает на рамку с током ориентирующие воздействие, поворачивая её. Это связано с
направлением магнитного поля, за которое берётся (в
данной точке) направление вдоль которого располагается положительная нормаль к контуру.
10.
За положительное направление может быть принятоp
направление, совпадающее с направлением силы, nm
которая действует на северный полюс магнитS
I
ной стрелки, помещенной в данную точку.
N
Так как, оба полюса магнитной стрелки лежат в близ- S
ких точках поля, то силы действующие на оба полюса
примерно равны друг другу. Значит, на магнитную
стрелку действует пара сил, поворачивающих её так,
что бы ось стрелки совпадала с направлением поля.
Рамка с током испытывает ориентирующее действие
поля, и на неё в магнитном поле действует пара сил.
Вращающий момент этих сил M зависит как от свойств
поля в данной точке, так и от свойств контура.
M pm B
11. МАГНИТНАЯ ИНДУКЦИЯ
B – ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ – силовая характеристика магнитного поля равная отношению силы,действующей со стороны магнитного поля dF на малый элемент проводника с электрическим током, и
произведения силы тока I на длину элемента dl .
1 dF
B
I dl max
Если в данную точку поля помещать контуры с разными
магнитными моментами, то на них действуют различные вращающие моменты, однако, отношение максимальных вращающих моментов M к магнитным моментам p m будет для всех контуров одинаковым.
M p m B const
12.
МАГНИТНАЯ ИНДУКЦИЯ – в точке однородного магнитного поля определяется максимальным вращающиммоментом, равным единице, когда
нормаль к контуру перпендикулярна направлению поля.
Так как магнитное поле является силовым, то его, как и электрическое изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора B . Их направление задается с помощью правила правого винта.
На рисунке показаны линии магнитной индукции полей
кругового тока и соленоида ( равномерно намотанной
на цилиндр спирали по которой течет ток).
13.
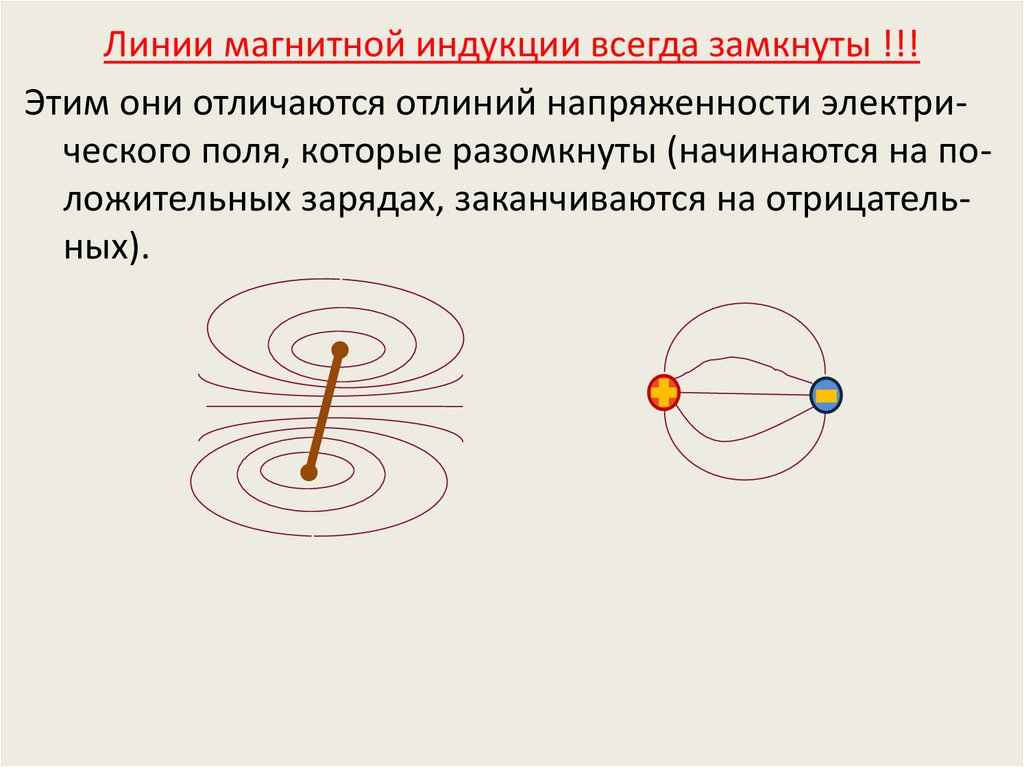
Линии магнитной индукции всегда замкнуты !!!Этим они отличаются отлиний напряженности электрического поля, которые разомкнуты (начинаются на положительных зарядах, заканчиваются на отрицательных).
14. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ
Ампер (1775-1836) предположил что в любом теле существуют микроскопические токи обусловленные движением электронов в атомах и молекулах. Эти микротокисоздают своё магнитное поле, и могут поворачиваться в
магнитном поле макротоков.
Если вблизи тела поместить проводник с током (макроток), то под действием его магнитного поля, микротоки
во всех атомах определенным образом ориентируются,
создавая в теле дополнительное магнитное поле. Магнитная индукция B характеризует результирующее магнитное поле, создаваемое всеми макро и микротоками.
То есть: при одном и том же токе и равных условиях,в
различных средах значения вектора магнитной индукции B будут иметь различные значения.
15.
Магнитное поле макротоков описывается ВЕКТОРОМНАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ H. Для однородной изотропной среды вектор магнитной индукции
связан с вектором напряженности соотношением:
B 0 H
7 Гн
0 4 10
– магнитная постоянная.
м
– магнитная проницаемость среды, показывающая
во сколько раз магнитное поле макротоков H усиливается за счет магнитного поля микротоков среды.
Сравнивая векторные характеристики электростатическокого E, D и магнитного H , B полей, можно заметить
что аналогом вектора электрического смещенияD является вектор напряженности магнитного поля H , а аналогом вектора напряженности электрического поля E ,
является вектор магнитной индукции B .
16. ЗАКОН БИО-САВАРА-ЛАПЛАСА
17. ЗАКОН БИО – САВАРА – ЛАПЛАСА
Магнитное поле постоянного тока изучалось dlr
I
французами Био (1774-1862), Саваром
A
(1791-1842) и результаты исследований
были обобщены Лапласом.
dB
Для проводника с током I , элемент которого dl создает в
некоторой точке А магнитное поле с индукцией dB
справедливо соотношение:
dB
0 Idl r
4 r 3
Закон Био – Савара - Лапласа
dl – вектор равный по модулю длине проводника dl и
совпадающий по направлению с током I .
r – радиус-вектор проведенный из элемента проводника dl в точку А поля ( r - его модуль).
18.
Направление dB перпендикулярно dl иr то есть перпендикулярно плоскости в которой они лежат, и совпадает скасательной к линиям магнитной индукции. Это направление может быть найдено с помощью правила
правого винта, где направление вращения головки dB
поступательное движение винта – направление тока I.
0 Idl sin
dB
4
r2
Закон Био – Савара – Лапласа в скалярной форме
n
– угол между векторами dl и r .
B Bi
1
Для магнитного как и для электрического полей iсправедлив ПРИНЦИП СУПЕРПОЗИЦИИ: Магнитная индукция
создаваемая в одной точке несколькими движущимися
зарядами или токами равна векторной сумме магнитных индукций создаваемых каждым током (зарядом) в
отдельности.
19. МАГНИТНОЕ ПОЛЕ ПРЯМОГО ТОКА
Магнитное поле тока текущего по прямому, dFl Dтонкому, бесконечно длинному проводу. C d
A
R
В произвольной точке А, удаленной от про- I
dB , B
водника на расстояние R , векторы dB от
всех элементов проводника с током dl имеют направление «к нам». Сложение этих векторов можно заменить суммой их модулей.
Так как dl 0 , то радиус дуги CD равен r и угол FDC 90
R
r
sin
rd
dl
sin
0 Idl sin 0 I
dB
sin d
2
4
4 R
r
Так как для всех элементов прямого тока изменяется
в пределах 0 : ,то полная магнитная индукция
0 I
0 2 I 0 I
B dB
sin d
4 R 0
4 R
2 R
20. МАГНИТНОЕ ПОЛЕ В ЦЕНТРЕ КРУГОВОГО ПРОВОДНИКА С ТОКОМ
Все элементы проводника в центре окружdB , Bности создают магнитное поле одинакогоR
во направления (вдоль нормали витка).
dl
I
Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы
перпендикулярны радиусу-вектору R sin 1 и расстояние всех элементов проводника до центра одинакого
I
dB
0
4 R
2
dl
dl 0;2 R
0 I 2 R
0 I
0 I
B dB
dl
2
R
4 R 2 0
4 R 2
2R
21. ЗАКОН АМПЕРА. ВЗАИМОДЕЙСТВИЕ ПАРАЛЛЕЛЬНЫХ ТОКОВ
22. ЗАКОН АМПЕРА
Магнитное поле ориентирует контур тока (рамку) в пространстве, значит, вращающий момент, испытываемыйрамкой, есть результат действия сил на её отдельные
элементы. Ампер установил , что сила dF действующая
на малый элемент dl равна геометрической сумме сил,
которые действуют со стороны магнитного поля и вывел закон:
Сила dF с которой магнитное поле действует на элемент
проводника dl с током , находящийся в магнитном
поле , равна произведению силы тока на векторное
произведение элемента длины проводника на магнитную индукцию поля.
dF Idl B
Закон Ампера в векторной форме
23.
dF IBdl sinЗакон Ампера в скалярной форме
Направление вектора dF может быть оп- B
dF
ределено по правилу левой руки:
dl
В ладонь входит вектор магнитной индукI
ции B , четыре пальца показывают
направление тока I в проводнике dl , большой палец
показывает направление силы dF действующей на
элемент проводника с током.
24. СИЛА ВЗАИМОДЕЙСТВИЯ ДВУХ ТОКОВ
Закон Ампера может примеB1няться для определения
I1
R
I2
силы взаимодействия двух
токов.
B2
dF2 dF1
Пусть расстояние между двумя параллельными проводниками с токами I 1 и I 2 равно R . Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник. Рассмотрим с какой
силой действует магнитное поле тока I 1на элемент dl
проводника с током I 2 . Ток I 1 создает вокруг себя магнитное поле, линии магнитной индукции которого
представляют собой концентрические окружности.
25.
Направление B1 задается правилом «правого винта»,его абсолютное значение:
0 I 1
B1
2 R
Направление силы dF1 с которой поле B1 действует на
участок dl второго проводника с током определяется
по правилу левой руки. Модуль силы :
0 I 1 I 2
dF1 I 2 B1 dl
dl
2 R
Аналогично для проводника с током I 2 :
0 I1 I 2
dF2 I1 B2 dl
dl
2 R
Два параллельных тока одинакового направления будут
притягиваться друг к другу с силой
0 I1 I 2
dF dF1 dF2
dl
2 R
26. МАГНИТНАЯ ПОСТОЯННАЯ. ЕДИНИЦЫ ИЗМЕРЕНИЯМАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
Если два параллельных проводника с токами находятсяв вакууме 1 , то сила их действия на единицу
проводника: dF 2I I
dl
0
4
1 2
R
Для определения численного значения магнитной постоянной 0 , воспользуемся определением ампера
(единицы измерения силы тока), согласно которому:
АМПЕР- сила неизменяющегося тока, который при
прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно
малого поперечного сечения, расположенного в
27.
вакууме на расстоянии 1 м один от другого, создаётмежду проводниками силу равную 2*10⁻⁷ Н на каждый метр длины.
Следовательно, если I1 I 2 1( A) и R 1( м) то
dF
2 10 7 ( H м)
dl
dFR4
7 1 4
7 H
7 Гн
0
2 10
4 10 ( 2 ) 4 10 ( )
2 1 1
м
dl 2 I 1 I 2
A
Гн
0 4 10 ( )
м
7
Где Гн (генри) единица индуктивности (НЕ ИНДУКЦИИ!!)
28.
Единица измерения магнитной индукции – Тл (Тесла).1 Тл – магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый
метр прямого проводника,перпендикулярного полю
с током 1 А.
Н
1Тл 1
А м
Единица измерения напряженности магнитного поля –
А/м (ампер/метр).
1 А/м – напряженность такого поля, магнитная индукция которого в вакууме 4π·10¯⁷ Тл.
29. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА
30.
Каждый проводник с током создает в пространстве магнитное поле. Ток – упорядоченное движение электрических зарядов. Значит любой движущийся заряд создает вокруг себя магнитное поле.Свободно двигающийся заряд q ( заряд двигающийся
с постоянной нерелятивистской скоростью ), создает в точке М, на расстоянии r магнитное поле с
B
индукцией B .
М
0 q r
B
r
3
q
4 r
Вектор B направлен перпендикулярно плоскости
в которой расположены r и . Его направление – поступательное движение правого винта, при его вращении от к r .
31.
Формула магнитной индукции свободно двигающегосязаряда в скалярной форме:
0 q
B
sin
2
4 r
Движущийся заряд по своим свойствам эквивалентен
элементу тока
Idl q
Эти закономерности справедливы только при малых
скоростях движущегося заряда, когда электрическое
поле свободно двигающегося заряда можно считать
электростатическим , то есть неподвижным зарядом в
той точке в которой находится двигающийся заряд.
32. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ
33. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД
Магнитное поле действует не только на проводники с током, но и отдельные движущиеся заряды.Сила действующая на электрический заряд q , движущийся в магнитном поле B со скоростью
q
называется:
Сила Лоренца
B
F q B
F
Направление силы Лоренца определяется по правилу
левой руки.
Для положительного заряда (q>0), большой палец указывает направление силы действующей на положительный заряд. Для отрицательного заряда наоборот.
34.
Абсолютное значение Силы Лоренца:F q B sin
α – угол между и B .
Магнитное поле действует только на движущиеся заряды
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, она изменяет только НАПРАВЛЕНИЕ скорости, но не изменяет её МОДУЛЯ. СИЛА
ЛОРЕНЦА НЕ СОВЕРШАЕТ РАБОТЫ.
Постоянное магнитное поле не совершает работы над
движущейся в ней заряженной частицей, и кинетическая энергия этой частицы при движении в магнитном
поле не изменяется.
35.
Если на движущийся электрический заряд помимо магнитного поля B действует и электрическое поле с напряженностью Е , то результирующая сила F приложенная к заряду равна векторной сумме сил действующих со стороны обоих полей.F qE q B
Формула Лоренца
36. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ
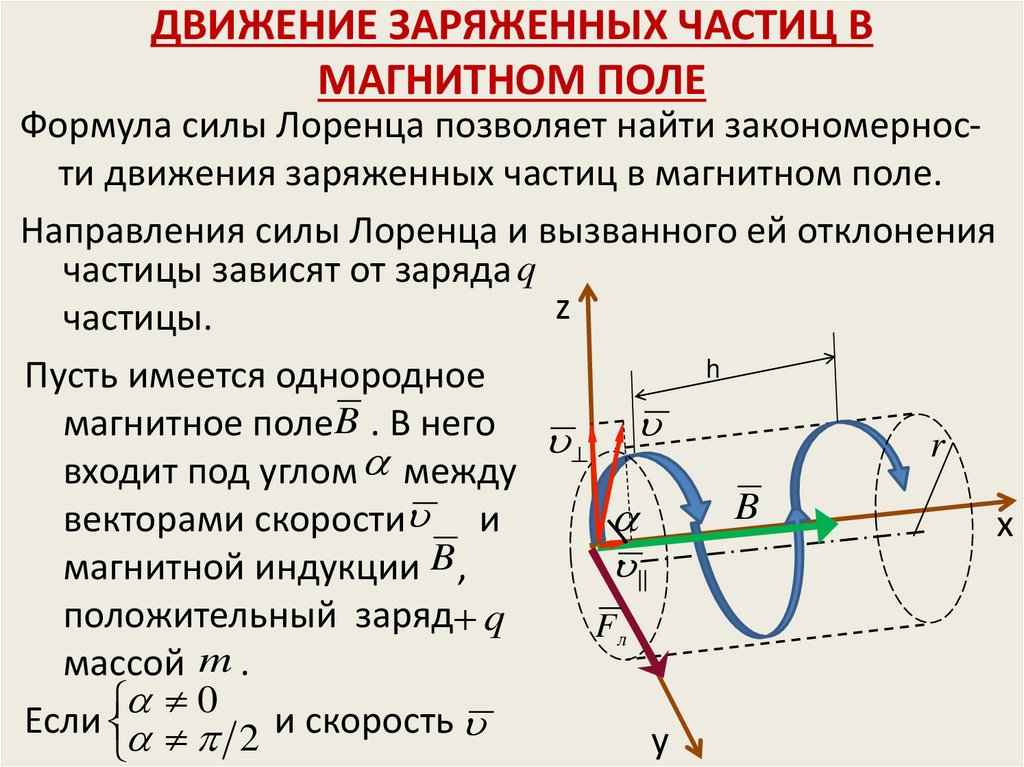
Формула силы Лоренца позволяет найти закономерности движения заряженных частиц в магнитном поле.Направления силы Лоренца и вызванного ей отклонения
частицы зависят от заряда q
z
частицы.
h
Пусть имеется однородное
магнитное полеB . В него
r
входит под углом между
B
векторами скорости и
x
||
магнитной индукции B ,
положительный заряд q
Fл
массой m .
0
Если 2 и скорость
y
37.
частицы направлена под углом к B , то её движениеможно представить в виде суперпозиции:
1) Равномерное прямолинейное движение вдоль поля
со скоростью || cos
2) Равномерное движение по окружности в плоскости
перпендикулярной полю со скоростью sin .
Радиус окружности:
m m sin
r
qB
qB
В результате сложения обоих движений, возникает движение по спирали, ось которой параллельна магнитному полю. Время затрачиваемое на один полный
оборот (Период заряда): T 2 r 2 m
qB
Шаг винтовой линии:
2 m
h \ \T
cos
qB
38.
Если заряд двигается ВДОЛЬ линий магнит- z 0ной индукции B , то есть 0 или ,
то Fл q B sin 0 и магнитное поле на
B
частицу НЕ ДЕЙСТВУЕТ и она двигается
прямолинейно и равномерно.
Если заряд двигается ПЕРПЕНДИКУЛЯРНО лиy
ниям магнитной индукции B , то есть B
и 2 , тоFл q B sin q B , постоян
z
на по модулю и нормальна ( ) к траекто2
рии частицы. По 2 закону Ньютона эта сила создает центростремительное ускоре- B
ние и частица будет двигаться по окружности которая определяется из условия
m 2
m
2 r 2 m
Fл q B
r
: T
r
qB
qB
y
x
x
39. ЭФФЕКТ ХОЛЛА
Эффект Холла – возникновение в металле (или полупроводнике) с током плотностью j , помещенном в магнитное поле B электрического поля в направленииперпендикулярном j и B.
Электроны подвергаются воздействию силы Лоренца и
концентрируются у одной из граней металла (эта грань
заряжается отрицательно, противоположная положительно). В результате между гранями возникает дополнительное электрическое поле.
Fл
Когда напряженность этого поля Е B
j
a
достигнет такой величины, что его
d
действие на заряды, будет уравно- B
вешивать силу Лоренца, то установится стационарное
40.
распределение зарядов в поперечном направлении.e
eE B
e B Ba
a
- поперечная (холловская) разность потенциалов.
I jS jad ne ad
n - концентрация электронов
I
1 IB
IB
Ba
Rx
nead
en d
d
Rx 1 en - постоянная Холла( зависит от вещества)
Холловская поперечная разность потенциалов прямо
пропорциональна магнитной индукции, силе тока, и
обратно пропорциональна толщине пластины. По измеренному значению разности потенциалов можно
определить концентрацию электронов в веществе.
Знак постоянной Холла совпадает со знаком носителя
заряда в веществе.
41. ЦИРКУЛЯЦИЯ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ
42.
Аналогично циркуляции вектора напряженности электростатического поля Е в вакууме, Циркуляцией вектора B по заданному замкнутому контуру называетсяинтеграл
B dl B dl
L
L
l
dl - вектор элементарной длины контура, направлен-
ной вдоль обхода контура
Bl B cos - составляющая вектора B в направлении касательной к контуру (с учетом выбранного направления обхода).
- угол между векторами B и dl .
43. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ (ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ)
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов охватываемых этим контуромn
B dl B dl I
l
L
L
0
i 1
i
n - число проводников с токами охватываемыми контуром L произвольной формы.
Циркуляция вектора Е всегда равна нулю, то есть электростатическое поле является потенциальным, Циркуляция вектора B не равна нулю. Магнитное поле – вихревое.
44. ПРИМЕР ЦИРКУЛЯЦИИ
B dl (0 I (1 1) I ( 1) I0
L
1
2
3
( 1 1 1 1 1 1) I 4 (1 1 1) I 5
( 1) I 6 1 I 7 ) 0 ( I 3 3I 5 I 6 I 7 )
I₃
I₁
I₆
I₂
I₄
I₅
I₇
• Каждый ток учитывается столько раз, сколько он
охватывается контуром.
• Положительным считается тот ток, направление которого связано с направлением обхода правилом правого винта.
• Данное выражение справедливо только для тока в
вакууме, так как для полей в веществе необходимо
учитывать и молекулярные токи.










































 physics
physics








