Similar presentations:
Магнитное поле тока
1.
Магнитное поле токаПЛАН
1. Магнитное поле и его характеристики
2. Закон Био — Савара — Лапласа
3. Закон Ампера. Взаимодействие
параллельных токов
4. Единицы измерения магнитных величин.
5. Сила Лоренца.
6. Циркуляция и поток вектора В для магнитного
поля в вакууме. Теорема Гаусса для поля
7. Магнитное поле соленоида и тороида.
8. Работа по перемещению проводника с током в
магнитном поле
9. Эффект Холла.
2.
1. Магнитное поле и его характеристики1820 г.
Х. Эрстед. На магнитную стрелку, расположенную
вблизи проводника с током, действуют силы,
которые стремятся повернуть стрелку.
А. Ампер. Силовое взаимодействие двух
проводников с токами. Закон взаимодействия
токов.
В пространстве, окружающем токи и постоянные
магниты, возникает силовое поле, называемое
магнитным.
Магнитное поле действует только на движущиеся в
этом поле электрические заряды
При исследовании магнитного поля используют
замкнутый плоский контур с током (рамка с
током)
3.
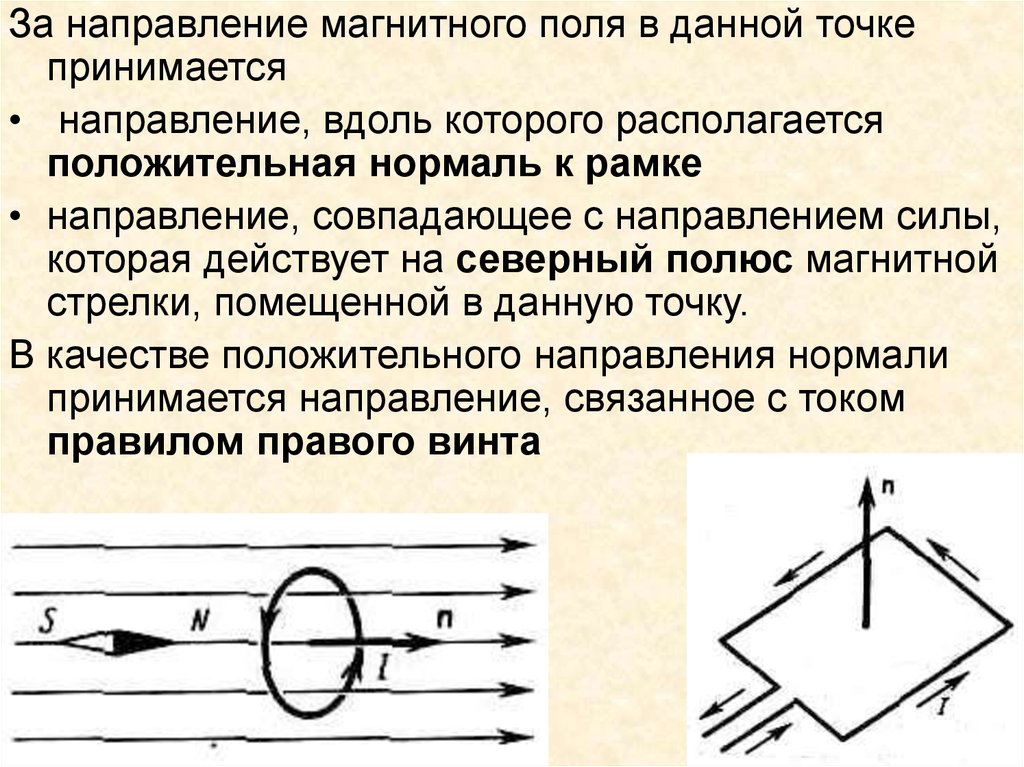
За направление магнитного поля в данной точкепринимается
• направление, вдоль которого располагается
положительная нормаль к рамке
• направление, совпадающее с направлением силы,
которая действует на северный полюс магнитной
стрелки, помещенной в данную точку.
В качестве положительного направления нормали
принимается направление, связанное с током
правилом правого винта
4.
• Рамка с током поворачивается в магнитном поле.• Вращающий момент сил зависит как от свойств
поля в данной точке, так и от свойств рамки:
M Pm B ,
M Pm B sin
• В - вектор магнитной индукции,
• Pm - вектор магнитного момента рамки с током.
• Для плоского контура с током I
Pm ISn,
Pm IS
• S - площадь поверхности контура (рамки),
• n - единичный вектор нормали к поверхности
рамки.
Направление Pm совпадает с направлением
положительной нормали.
5.
Магнитная индукция в данной точке однородногомагнитного поля определяется максимальным
вращающим моментом, действующим на рамку с
магнитным моментом, равным единице, когда
нормаль к рамке перпендикулярна направлению
поля
M max
B
Pm
Вектор магнитной индукции В может быть выведен
также из закона Ампера и из выражения для силы
Лоренца.
6.
Магнитное поле изображают с помощью линиймагнитной индукции — линий, касательные к
которым в каждой точке совпадают с
направлением вектора В.
Их направление задается правилом правого винта.
Линии магнитной индукции всегда замкнуты и
охватывают проводники с током.
Магнитное поле не имеет источников – магнитных
зарядов. Силовые поля, обладающие этим
свойством, называются вихревыми.
7.
8.
• Гипотеза А. Ампера: в любом теле существуютмикроскопические токи, обусловленные движением
электронов в атомах и молекулах.
• Молекулярные токи создают свое магнитное поле и
могут поворачиваться в магнитных полях
макротоков.
• Вектор магнитной индукции В характеризует
результирующее магнитное поле, создаваемое
всеми макро- и микротоками
• Магнитное поле макротоков описывается
вектором напряженности Н.
• Для однородной изотропной среды:
В= 0 Н,
0 — магнитная постоянная
— магнитная проницаемость среды,
показывающая, во сколько раз магнитное поле
макротоков Н усиливается за счет поля микротоков
среды.
9.
2. Закон Био — Савара — ЛапласаМагнитное поле постоянных токов различной формы
изучалось французскими учеными Ж. Био и Ф.
Саваром.
Результаты этих опытов были обобщены
французским математиком и физиком П.
Лапласом.
Принцип суперпозиции:
Если магнитное поле создается несколькими
проводниками с током, то индукция
результирующего поля есть векторная сумма
индукций полей, создаваемых каждым
проводником в отдельности.
B Bi
n
i 1
10.
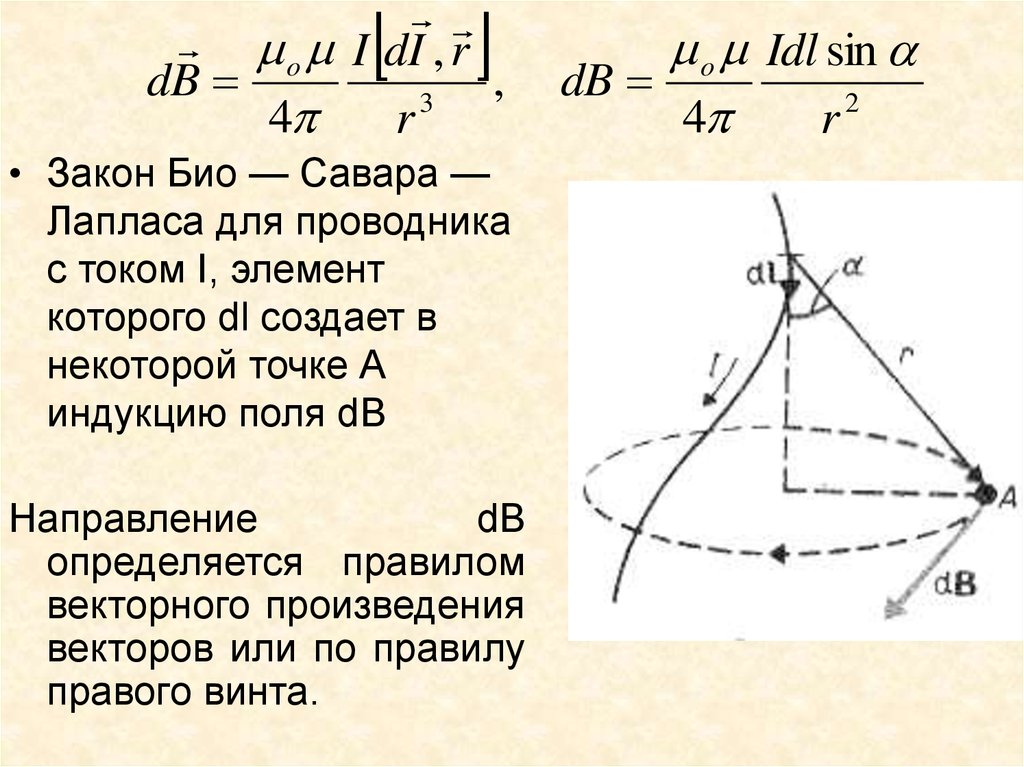
o I dI , rdB
,
3
4
r
• Закон Био — Савара —
Лапласа для проводника
с током I, элемент
которого dl создает в
некоторой точке А
индукцию поля dB
Направление
dB
определяется правилом
векторного произведения
векторов или по правилу
правого винта.
o Idl sin
dB
2
4
r
11.
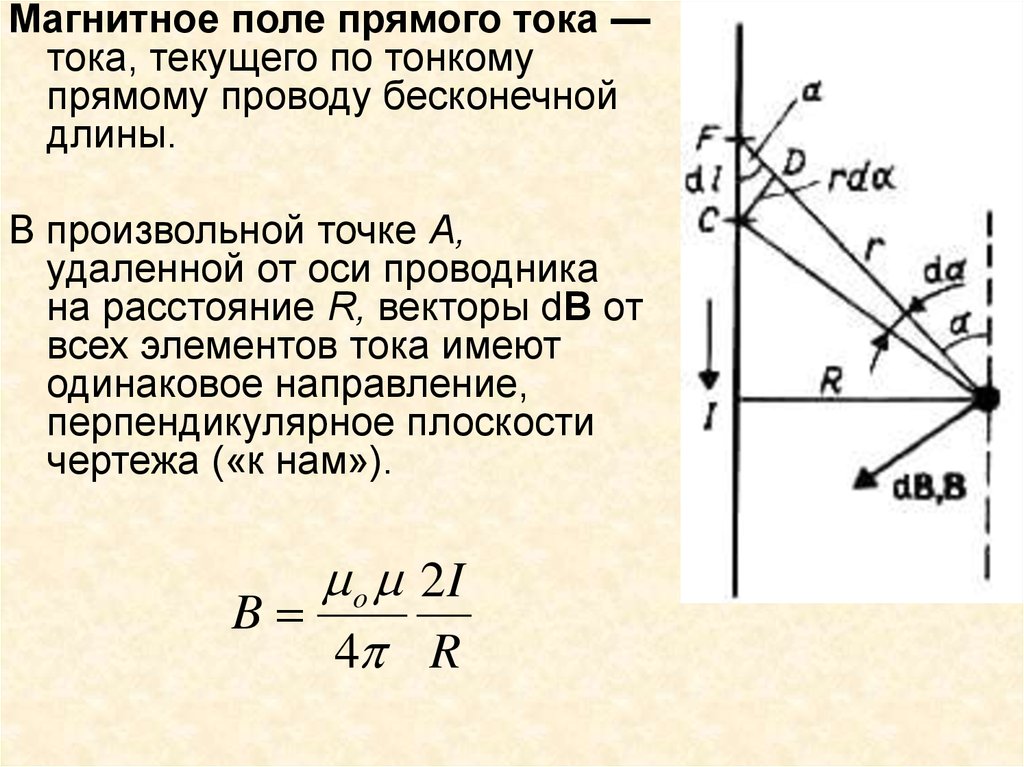
Магнитное поле прямого тока —тока, текущего по тонкому
прямому проводу бесконечной
длины.
В произвольной точке А,
удаленной от оси проводника
на расстояние R, векторы dB от
всех элементов тока имеют
одинаковое направление,
перпендикулярное плоскости
чертежа («к нам»).
o 2I
B
4 R
12.
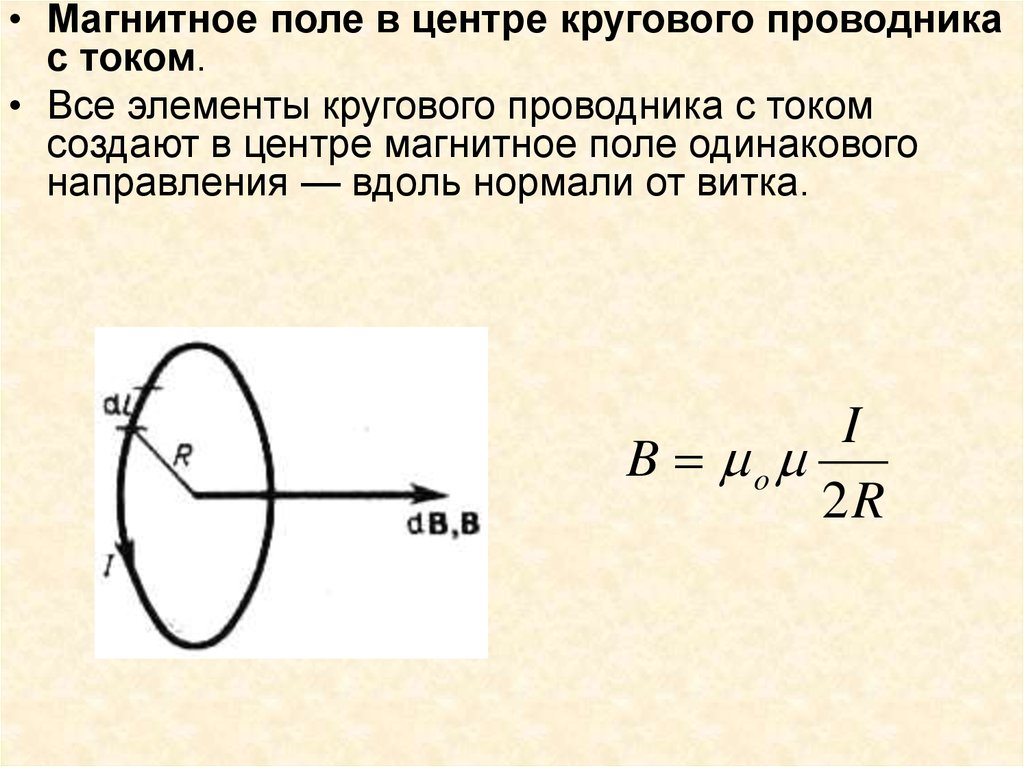
• Магнитное поле в центре кругового проводникас током.
• Все элементы кругового проводника с током
создают в центре магнитное поле одинакового
направления — вдоль нормали от витка.
I
B o
2R
13. 3. Закон Ампера
АМПЕР Андре Мари (1775 –1836)
–
французский
физик
математик и химик.
Основные физические работы
посвящены
электродинамике.
Сформулировал
правило
для
определения действия магнитного
поля тока на магнитную стрелку.
Обнаружил влияние магнитного поля
Земли на движущиеся проводники с
током.
14.
В 1820 г. А. М. Ампер экспериментально установил,что два проводника с током взаимодействуют друг с
другом с силой:
I1 I 2
F k
b
где b – расстояние между проводниками, а k –
коэффициент пропорциональности зависящий от
системы единиц.
15.
В современной записи в системе СИ, закон Амперавыражается формулой:
dF I [d l , B]
Это сила с которой магнитное поле действует на
бесконечно малый проводник с током I.
Модуль силы действующей на проводник
dF IBdlsin d l ,B .
16.
Если магнитное поле однородно и проводникперпендикулярен силовым линиям магнитного поля,
то
F IlB,
Работа силы Ампера
dA FA dх I B dх
dA I ( B dõ cos )
dA I d
17.
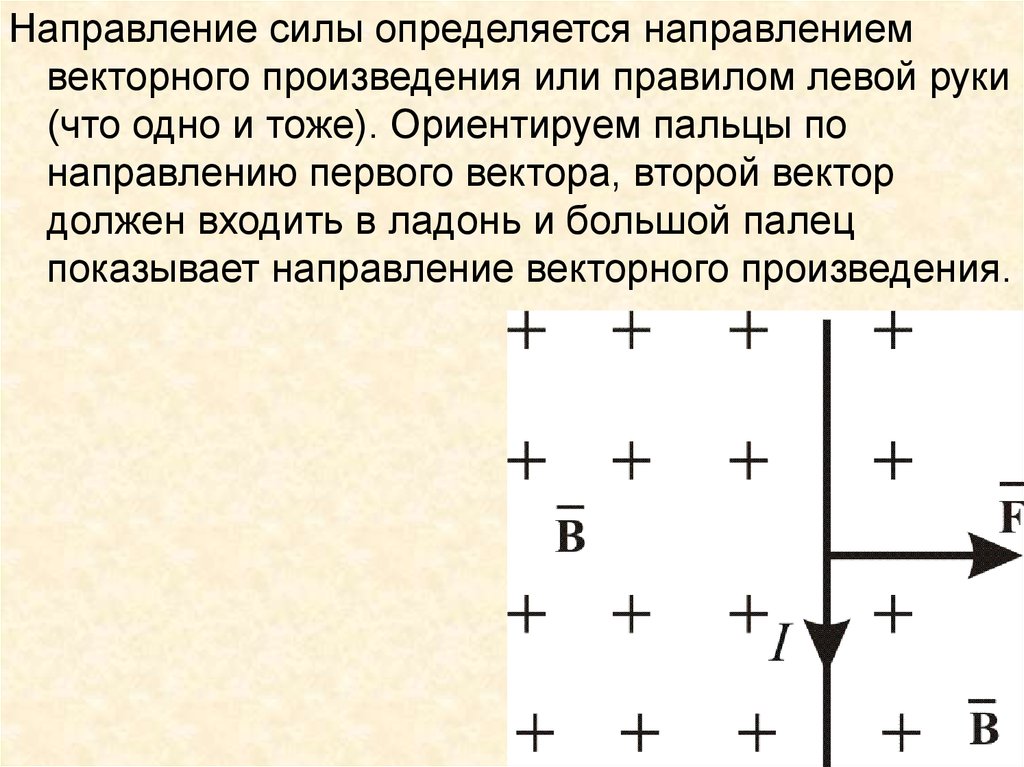
Направление силы определяется направлениемвекторного произведения или правилом левой руки
(что одно и тоже). Ориентируем пальцы по
направлению первого вектора, второй вектор
должен входить в ладонь и большой палец
показывает направление векторного произведения.
18.
Физический смысл магнитной индукции:В – величина, численно равная силе, с которой
магнитное поле действует на проводник единичной
длины, по которому течет единичный ток.
B
F
Il
Размерность индукции
Н
B
.
А м
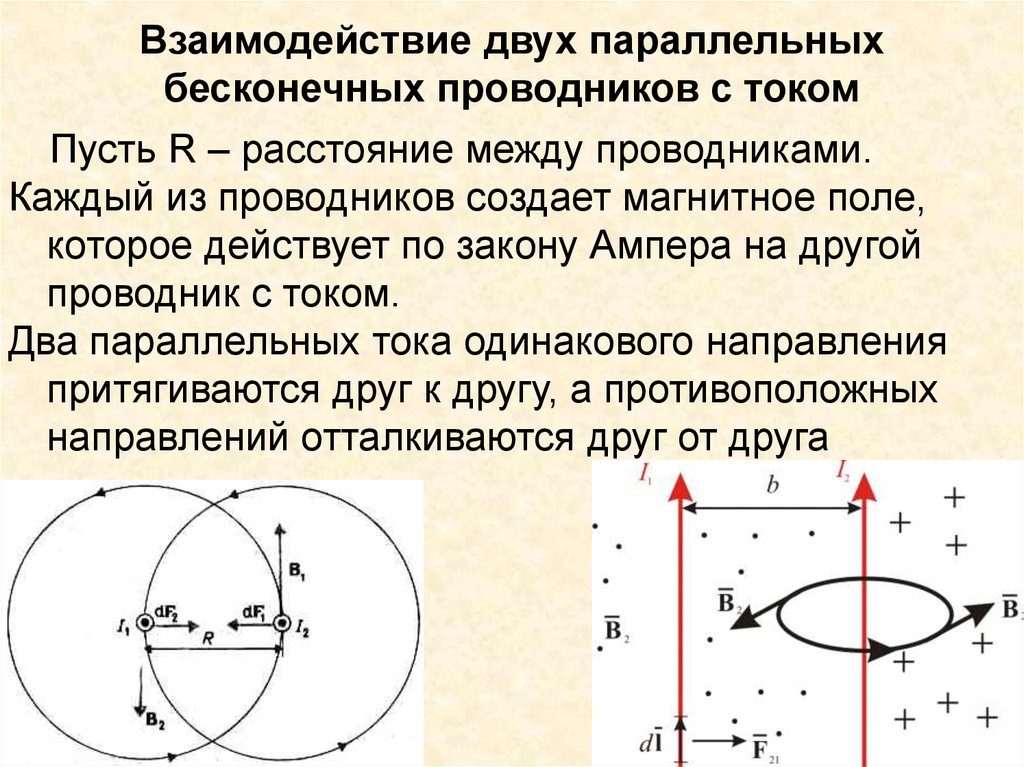
19. Взаимодействие двух параллельных бесконечных проводников с током
Пусть R – расстояние между проводниками.Каждый из проводников создает магнитное поле,
которое действует по закону Ампера на другой
проводник с током.
Два параллельных тока одинакового направления
притягиваются друг к другу, а противоположных
направлений отталкиваются друг от друга
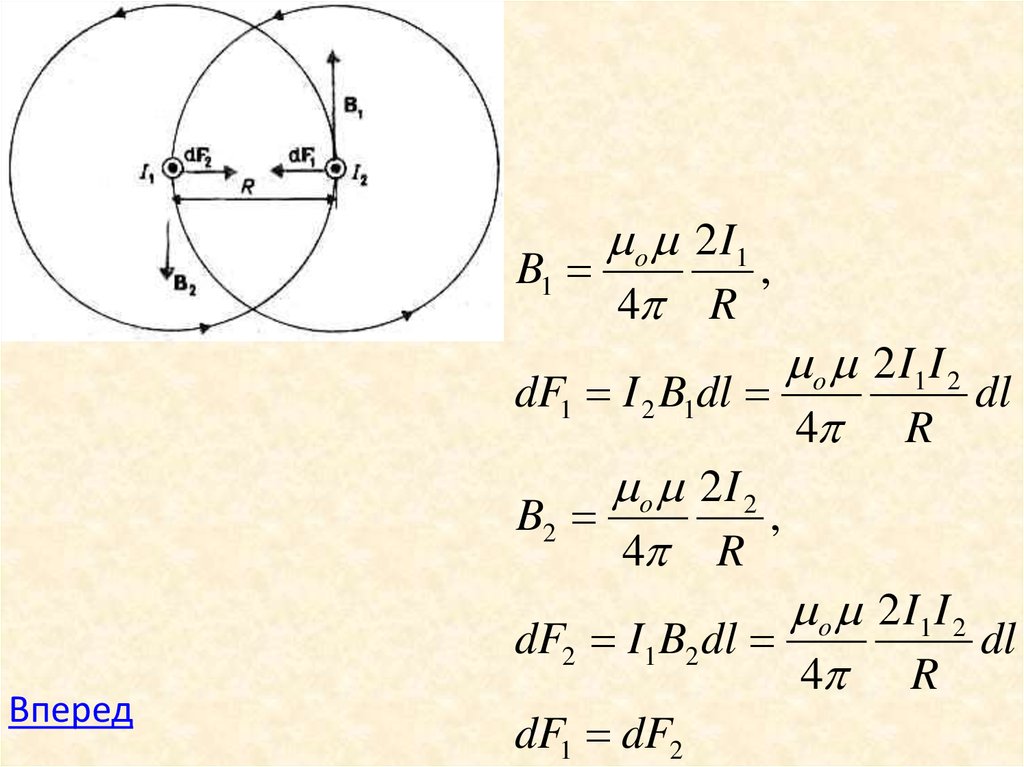
20.
o 2 I1B1
,
4 R
Вперед
o 2 I1 I 2
dF1 I 2 B1dl
dl
4 R
o 2 I 2
B2
,
4 R
o 2 I1 I 2
dF2 I1 B2 dl
dl
4 R
dF1 dF2
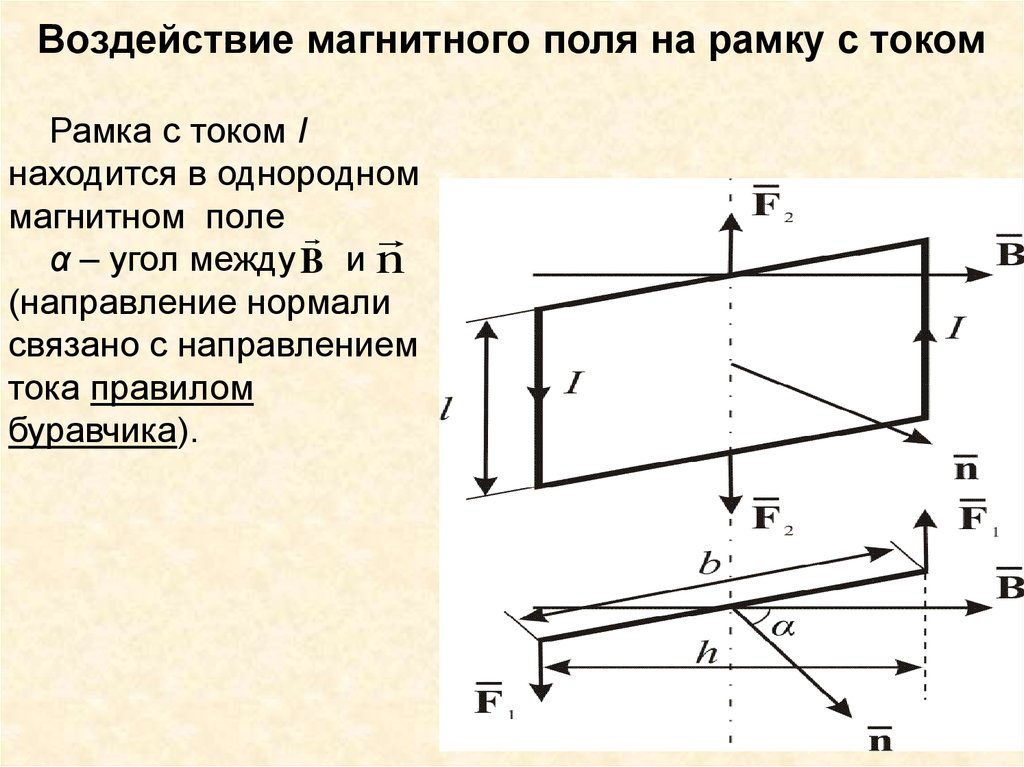
21. Воздействие магнитного поля на рамку с током
Рамка с током Iнаходится в однородном
магнитном поле
α – угол между B и n
(направление нормали
связано с направлением
тока правилом
буравчика).
B
n
22.
• Сила Ампера, действующая на сторону рамкидлиной l, равна:
F1 IlB
• Вращающий момент равен:
M F1h IlBb sin , h b sin .
M IBS sin BPm sin
M
B
Pm sin
M м акс
B
Pm
M – вращающий момент силы,
P – магнитный момент.
23. 4. Единицы измерения магнитных величин
Закон Ампера используется для установленияединицы силы тока – ампер.
dF
2I I
0
dl 4 R
1
dl 1 м R 1 м I1 I 2 1 А
dF
7 Н
2 10
.
dl
м
2
24.
Ампер – сила тока неизменного по величине,который, проходя по двум параллельным
прямолинейным проводникам бесконечной длины и
ничтожно малого сечения, расположенным на
расстоянии один метр, один от другого в вакууме
7
вызывает между этими проводниками силу 2 10 Í
• Тогда
0
2
2 10 Í
2À
4
7
Н
0 4 10
А2
7
Гн
0 4 10
м
7
0 I
B
4 b
Н А
Н
[ B] 2
1Тл
А м А м
25.
1 Тл (один тесла равен магнитной индукцииоднородного магнитного поля, в котором) на плоский
контур с током, имеющим магнитный момент 1 А·м2
действует вращающий момент 1 Н·м.
1 Тл равен магнитной индукции при которой
магнитный поток сквозь площадку 1 м2,
перпендикулярную направлению поля равен 1 Вб
dÔ B Bd S cos(dn, B)
Ф Bn dS .
S
26.
ТЕСЛА Никола (1856 - 1943)сербскийученый
в
области
электротехники, радиотехники
Разработал
ряд
конструкций
многофазных генераторов, электродвигателей
и
трансформаторов. Сконструировал ряд радиоуправляемых
самоходных
механизмов.
Изучал физиологическое действие
токов высокой частоты. Построил в
1899 радиостанцию на 200 кВт в
Колорадо и радиоантенну высотой
57,6 м в Лонг-Айленде. Изобрел
электрический счетчик, частотомер
и др.
27.
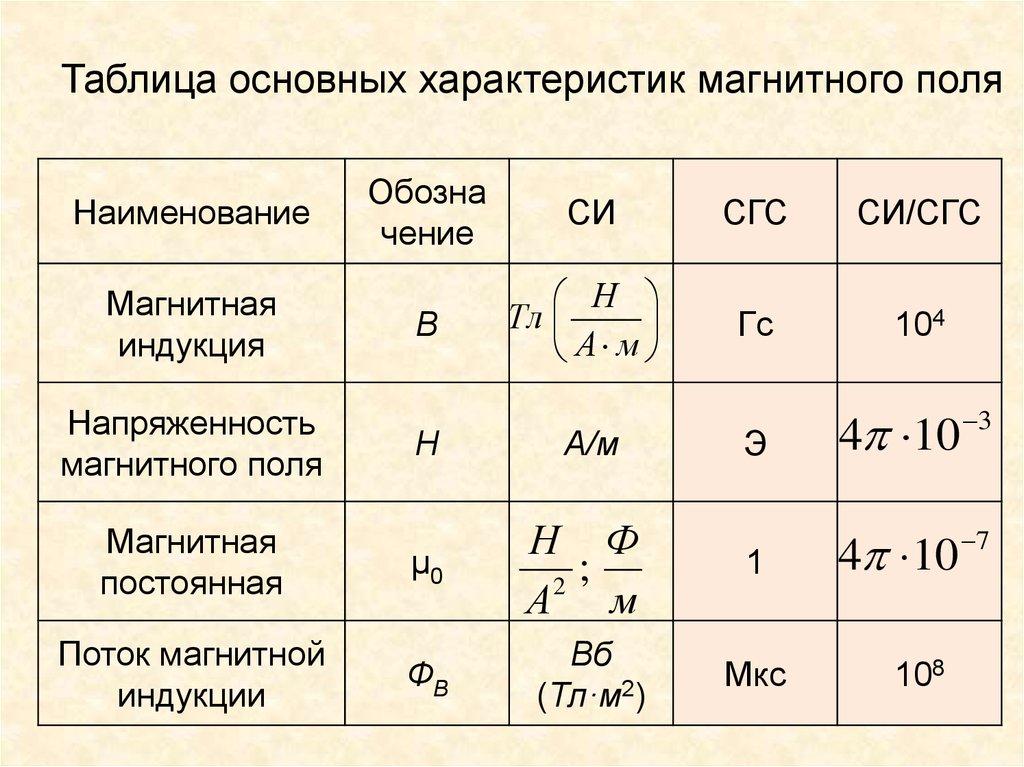
Таблица основных характеристик магнитного поляНаименование
Магнитная
индукция
Напряженность
магнитного поля
Магнитная
постоянная
Поток магнитной
индукции
Обозна
чение
СИ
СГС
СИ/СГС
В
Н
Тл
А м
Гс
104
Э
4 10
3
μ0
Н Ф
;
2
А м
1
4 10
7
ФB
Вб
(Тл·м2)
Мкс
Н
А/м
108
28.
5. Сила ЛоренцаСила, действующая на электрический заряд q во
внешнем электромагнитном поле, зависит не только
от
его
местоположения
и
напряженности
электрического поля E(x,y,z) в этой точке: qE(x,y,z),
но, в общем случае, и от скорости его движения v и
величины индукции магнитного поля В(x,y,z).
Выражение для этой силы было получено в конце
XIX в. голландским физиком Г.А. Лоренцем
29. Получим формулу для расчета силы Лоренца
Найдем силу, действующую на один заряд состороны магнитного поля.
По закону Ампера сила, действующая на
проводник с током в магнитном поле
ток
I jS ,
dF I [d l , B]
причем
j qn
, тогда
dF qn S d l , B qnSdl v, B ,
30.
• Т.к. nSdl –число зарядов в объёме Sdl, тогда дляодного заряда
dF
q ,B ,
nSdl
Fл q[ , B]
Fл q B sin
31.
ЛОРЕНЦ Хендрик Антон (1853 - 1928) –нидерландский физик-теоретик, создатель
классической электронной теории, член
Нидерландской АН.
Вывел формулу, связывающую
диэлектрическую проницаемость с
плотностью диэлектрика, дал выражение для
силы, действующей на движущийся заряд в
электромагнитном поле (сила Лоренца),
объяснил зависимость электропроводности
вещества от теплопроводности, развил
теорию дисперсии света. Разработал
электродинамику движущихся тел.
В 1904 вывел формулы, связывающие
между собой пространственные координаты
и моменты времени одного и того же
события в двух различных инерциальных
системах отсчета (преобразования Лоренца).
32.
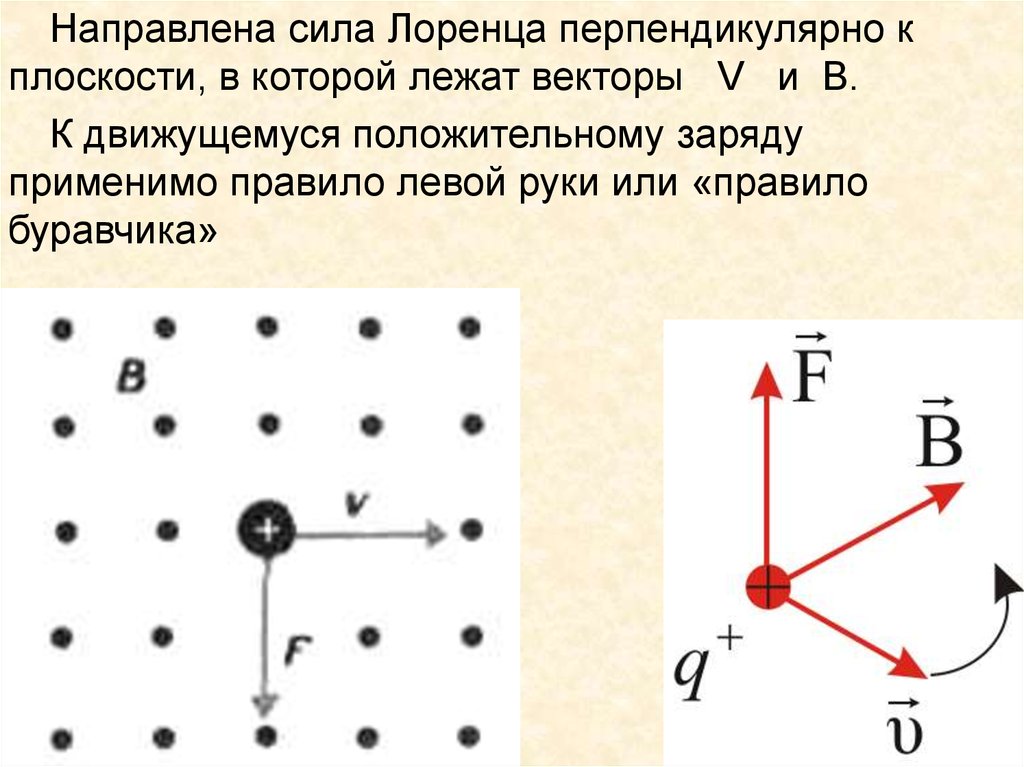
Направлена сила Лоренца перпендикулярно кплоскости, в которой лежат векторы V и B.
К движущемуся положительному заряду
применимо правило левой руки или «правило
буравчика»
33.
• Направление действия силы для отрицательногозаряда – противоположно, следовательно, к
электронам применимо правило правой руки.
A FË dr cos 0, cos cos 90 0
• Часто лоренцевой силой называют сумму
электрических и магнитных сил:
Fл qE q[ v, B]
34.
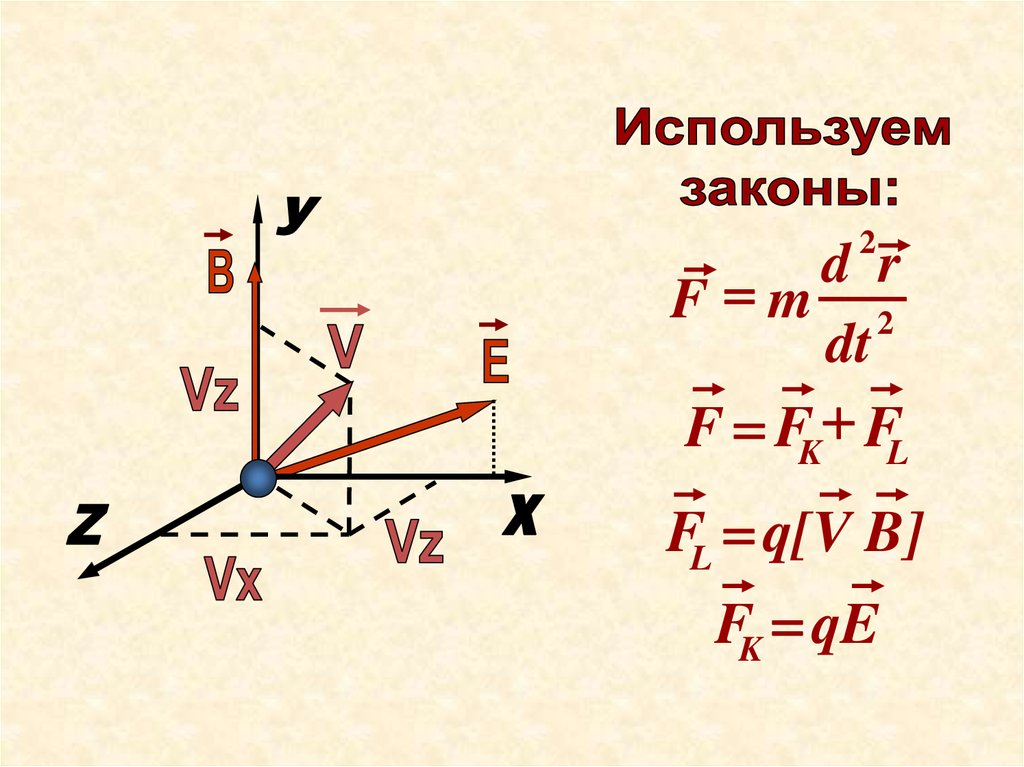
2d r
F m 2
dt
F FK FL
FL q[V B]
FK qE
35.
Основные выводыСила Лоренца:
Полная
сила,
действующая
электромагнитном поле, равна
на
заряд
в
F QE Q[ , B]
Магнитная
составляющая
силы
Лоренца
перпендикулярна вектору скорости, элементарная
работа этой силы равна нулю.
Cила Fm меняет направление движения, но не
величину скорости.
Модель
Пример
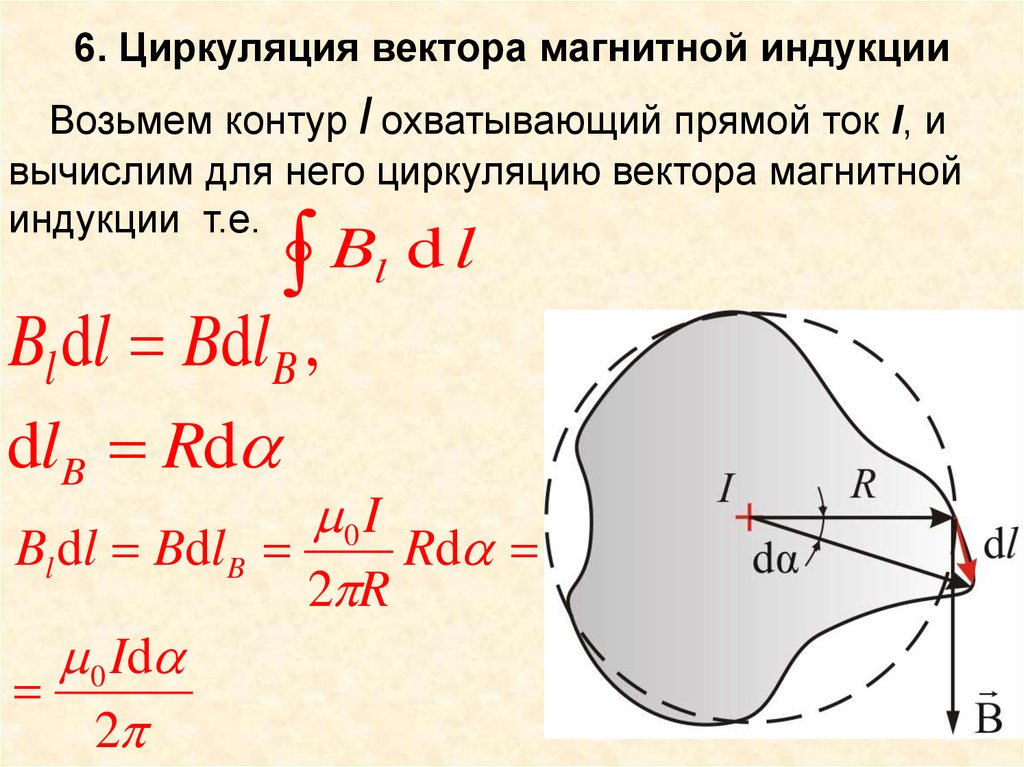
36. 6. Циркуляция вектора магнитной индукции
Возьмем контур l охватывающий прямой ток I, ивычислим для него циркуляцию вектора магнитной
индукции т.е.
B
Bl dl Bdl B ,
dlB Rd
l
dl
0 I
Bl dl Bdl B
Rd
2 R
0 Id
2
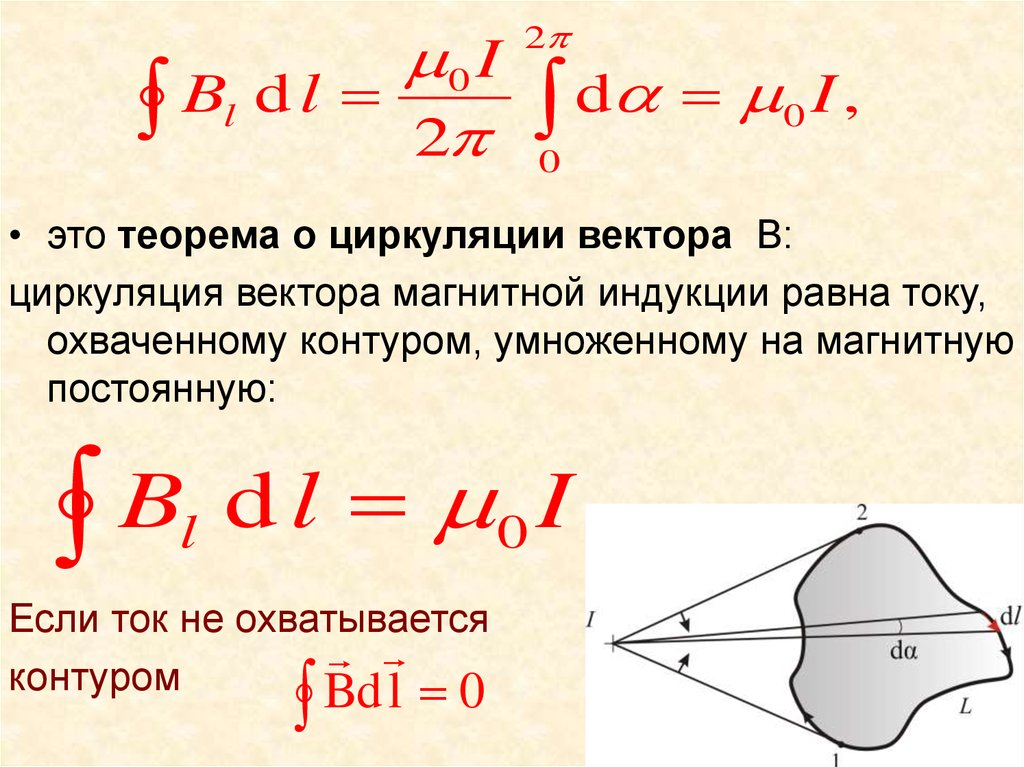
37.
0 IB
d
l
l
2
2
d
I
,
0
0
• это теорема о циркуляции вектора B:
циркуляция вектора магнитной индукции равна току,
охваченному контуром, умноженному на магнитную
постоянную:
B
d
l
I
0
l
Если ток не охватывается
контуром
Bd l 0
38.
• Если контур охватывает несколько токов, тоB
d
l
I
l
0
i
• циркуляция вектора B равна алгебраической
сумме токов, охваченных контуром
произвольной формы.
• Магнитные поля называют вихревыми или
соленоидальными.
Магнитному полю нельзя приписывать потенциал.
E
dl
0
l
39.
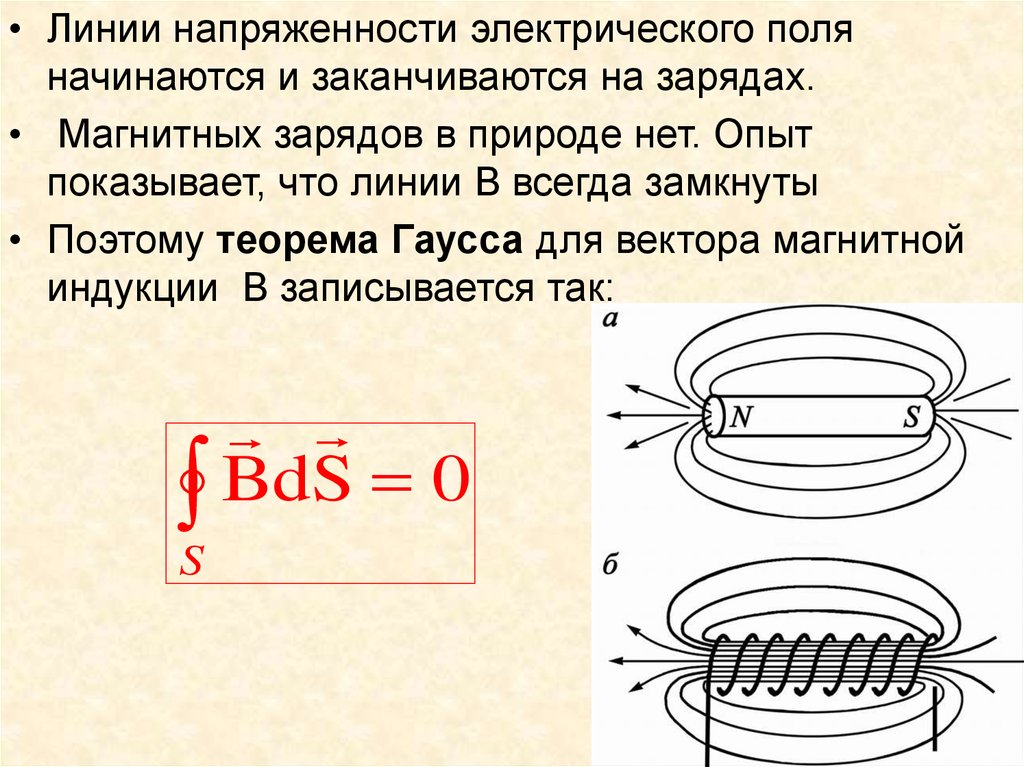
• Линии напряженности электрического поляначинаются и заканчиваются на зарядах.
• Магнитных зарядов в природе нет. Опыт
показывает, что линии B всегда замкнуты
• Поэтому теорема Гаусса для вектора магнитной
индукции B записывается так:
B
d
S
0
S
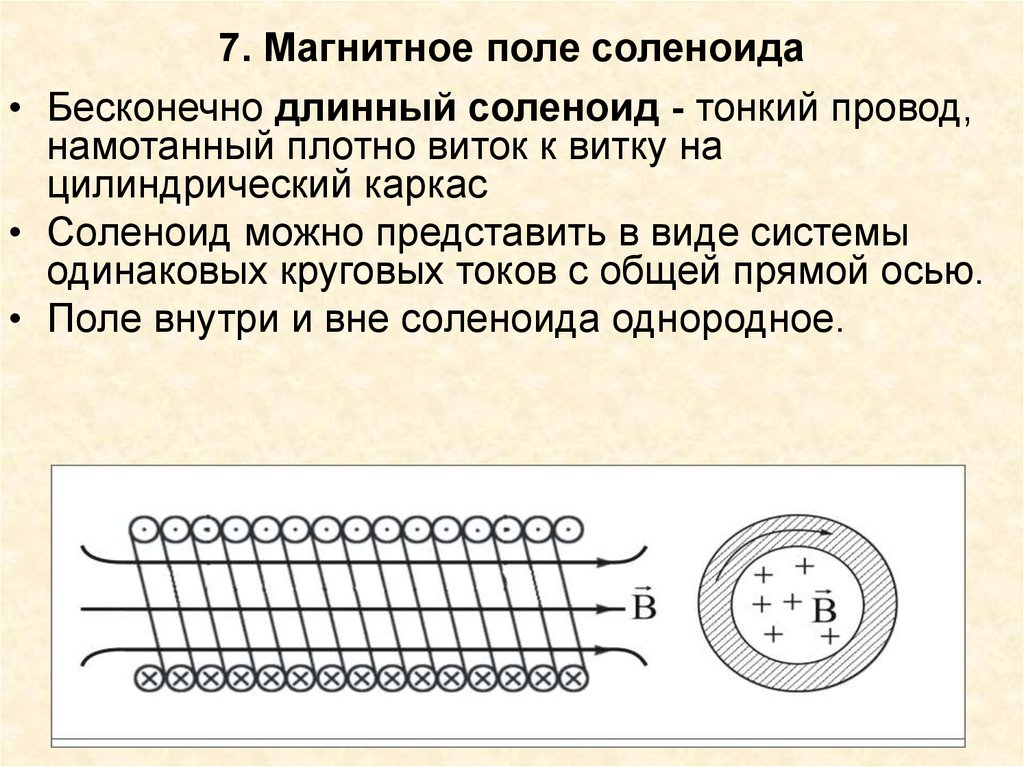
40. 7. Магнитное поле соленоида
• Бесконечно длинный соленоид - тонкий провод,намотанный плотно виток к витку на
цилиндрический каркас
• Соленоид можно представить в виде системы
одинаковых круговых токов с общей прямой осью.
• Поле внутри и вне соленоида однородное.
41.
• магнитная индукция внутри соленоидаB 0 nI .
• где n – число витков на единицу длины, I – ток в
соленоиде (в проводнике).
• Вне соленоида:
B
d
l
Bl
0
I
0
l
i
B 0
• Бесконечно длинный соленоид аналогичен
плоскому конденсатору.
• Произведение nI – называется число ампер
витков на метр.
42.
-В точке, лежащей на середине оси конечногосоленоида магнитное поле будет максимальным:
Bmax 0 nI
L
4R L
2
2
,
где L – длина соленоида, R – диаметр витков.
-В произвольной точке конечного соленоида
1
B 0 nI (cos 1 cos 2 ).
2
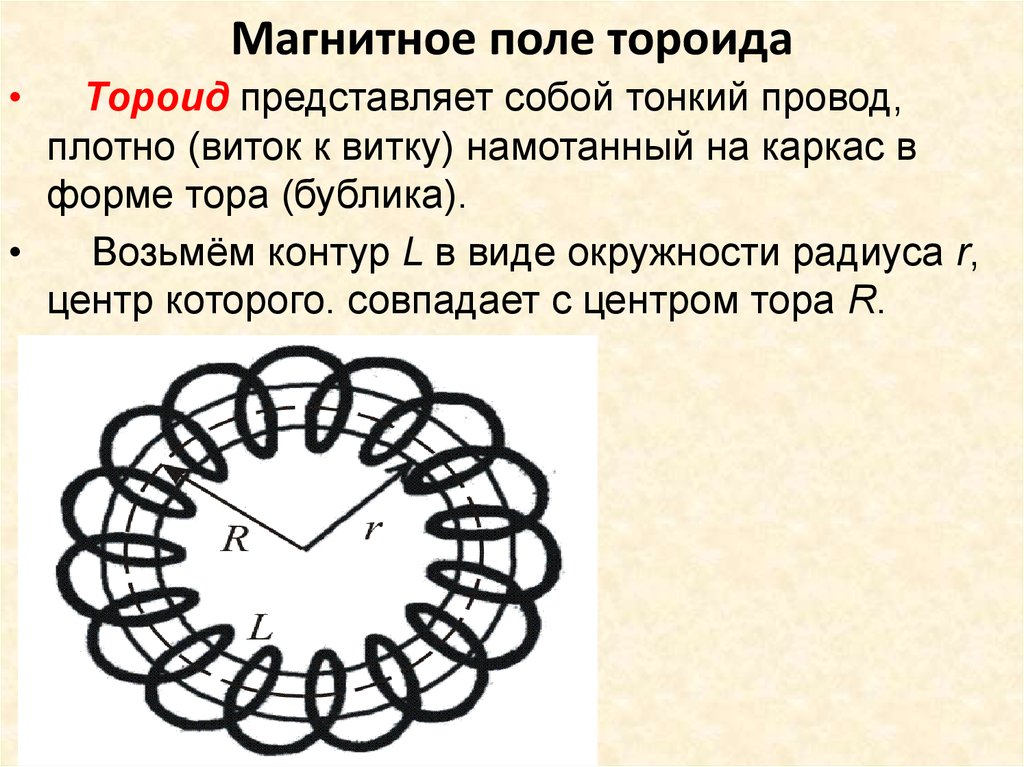
43. Магнитное поле тороида
Тороид представляет собой тонкий провод,
плотно (виток к витку) намотанный на каркас в
форме тора (бублика).
Возьмём контур L в виде окружности радиуса r,
центр которого. совпадает с центром тора R.
44.
Внутри тора
R
B 0 nI
r
• Контур вне тороида токов не охватывает,
поэтому вне тороида
B 0
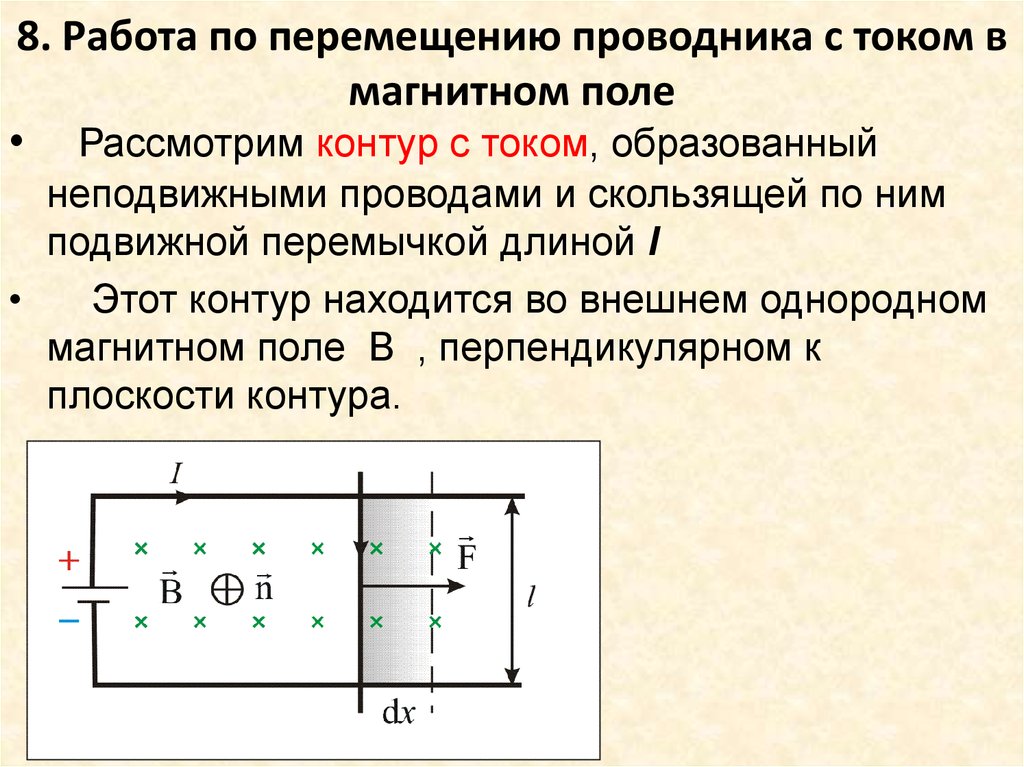
45. 8. Работа по перемещению проводника с током в магнитном поле
• Рассмотрим контур с током, образованныйнеподвижными проводами и скользящей по ним
подвижной перемычкой длиной l
Этот контур находится во внешнем однородном
магнитном поле B , перпендикулярном к
плоскости контура.
46.
На элемент тока I (подвижный провод) длиной lдействует сила Ампера, направленная вправо:
F IlB.
Пусть проводник переместится параллельно самому
себе на расстояние dx. При этом совершится
работа:
dA Fdx IBldx IBdS IdФ.
d
A
I
d
Ф
.
Работа, совершаемая проводником с током при
перемещении, численно равна произведению
тока на магнитный поток, пересечённый этим
проводником.
47. 9. Эффект Холла
• Одним из проявлений магнитной составляющейсилы Лоренца в веществе служит эффект,
обнаруженный в 1879 г. американским физиком
Э.Г. Холлом (1855–1938).
• Эффект Холла состоит в возникновении на
боковых гранях проводника с током,
помещенного в поперечное магнитное поле,
разности потенциалов, пропорциональной
величине тока I и индукции магнитного поля В.
48.
Представим себе проводник в виде плоской ленты,расположенной в магнитном поле с индукцией B
направленной от нас.
В случае а) верхняя часть проводника будет
заряжаться отрицательно, в случае б) положительно.
49.
• Это позволяет экспериментально определить знакносителя заряда в проводнике.
• При равной концентрации носителей заряда обоих
знаков возникает холловская разность
потенциалов.
• Подсчитаем величину холловской разности
потенциалов (Uх).
• Обозначим: Ex – напряженность электрического
поля, обусловленного ЭДС Холла, h – толщина
ленты проводника.
U x E x h.
50.
• Перераспределение зарядов прекратится, когдасила qEx уравновесит лоренцеву силу, т.е.
или
qEx q B
Ex B .
j
j n q
Ex B
nq
jBh
BhI BI RBI
Ux
или U x
,
nq
nqS qna
a
j
nq
• Где
R 1 / qn
– коэффициент Холла.
51.
Холловская разность потенциаловBI RBI
Ux
qna
a
Где
R 1 / qn
– коэффициент Холла.
52.
Исследования ЭДС Холла привели к
удивительным выводам:
• Металлы могут обладать проводимостью р –типа
(Zn, Cd – у них дырки более подвижные, чем
электроны).
• Это металлы с чуть перекрывающимися знаками,
т.е. полуметаллы.
53.
Число носителей заряда:IB
n
qaU x
Измерение Холловской разности потенциалов
позволяет определить:
1) знак заряда;
2) количество носителей.




















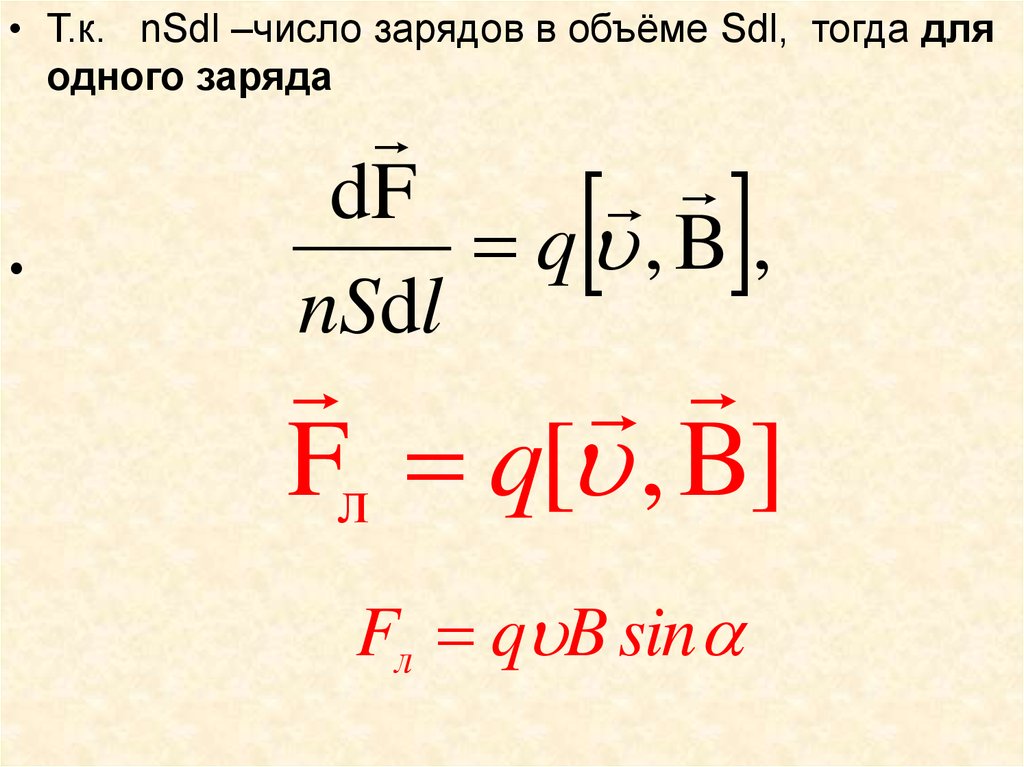















 physics
physics








