Similar presentations:
Магнитное поле в вакууме. Лекция 5
1. Лекция 5-2020. Магнитное поле в вакууме
Вектор индукции и напряженности магнитного поляЗакон Био-Савара-Лапласа
Принцип суперпозиции магнитных полей
Поле прямого и кругового тока
Поток вектора магнитной индукции
Теорема Гаусса для магнитного поля
Теорема о циркуляции вектора индукции магнитного
поля в интегральной и дифференциальной формах
8. Расчет магнитного поля тороида и соленоида.
1.
2.
3.
4.
5.
6.
7.
2.
Магнитный поток мы должны признатьподлинной физической реальностью, а
не чем-то воображаемым.
В.Ф. Миткевич
Из всего комплекса фарадеевских
представлений о магнитных линиях особо
существенное значение имеет
представление об их непрерывности
В.Ф. Миткевич
Чуев А.С. - 2020
2
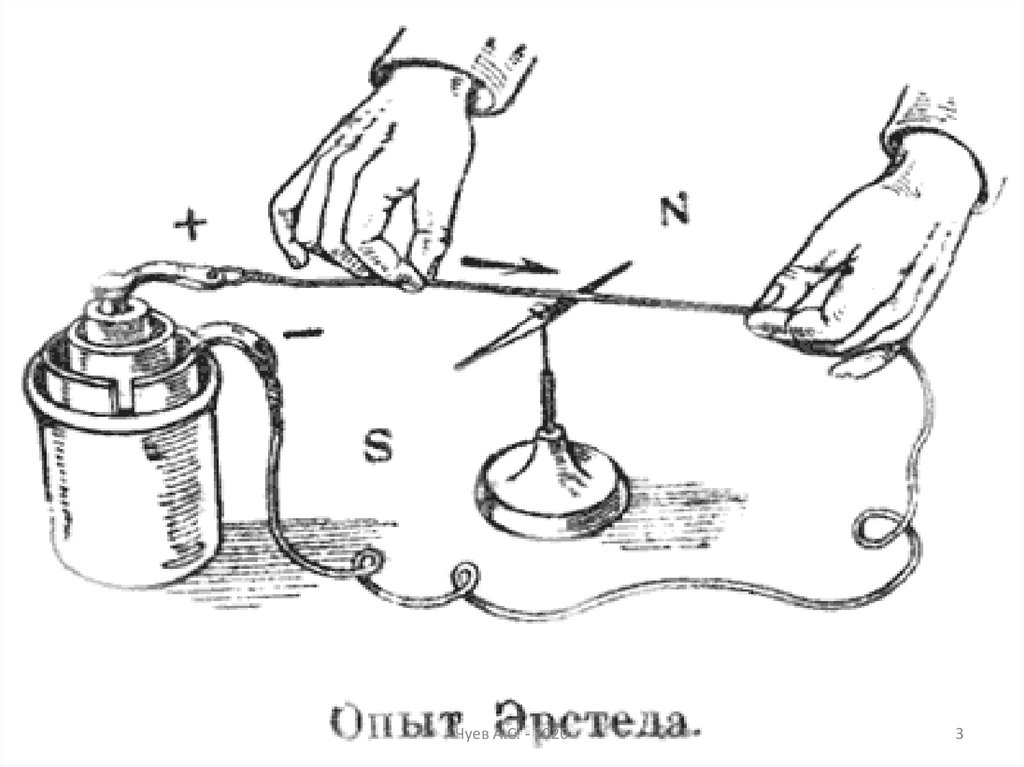
3.
Чуев А.С. - 20203
4.
Магнитная индукция B характеризуетсиловое действие
магнитного поля на ток
(аналогично, E характеризует силовое действие
электрического поля на заряд).
B – силовая характеристика магнитного поля, ее можно
изобразить с помощью магнитных силовых линий.
магнитное поле – вихревое не потенциальное
поле.
Чуев А.С. - 2020
4
5.
Условились, за направление B принимать
направление северного конца магнитной стрелки.
• Силовые линии выходят из северного полюса, а
входят, соответственно, в южный полюс магнита.
• Для графического изображения полей удобно пользоваться
силовыми линиями (линиями магнитной индукции).
Линиями магнитной индукции называются кривые,
касательные к которым в каждой точке совпадают с
направлением вектора B в этой точке.
Чуев А.С. - 2020
5
6.
Конфигурациюсиловых линий легко
установить с помощью
мелких железных опилок
которые
намагничиваются
в
исследуемом магнитном
поле и ведут себя
подобно
маленьким
магнитным
стрелкам
(поворачиваются вдоль
силовых линий).
Чуев А.С. - 2020
6
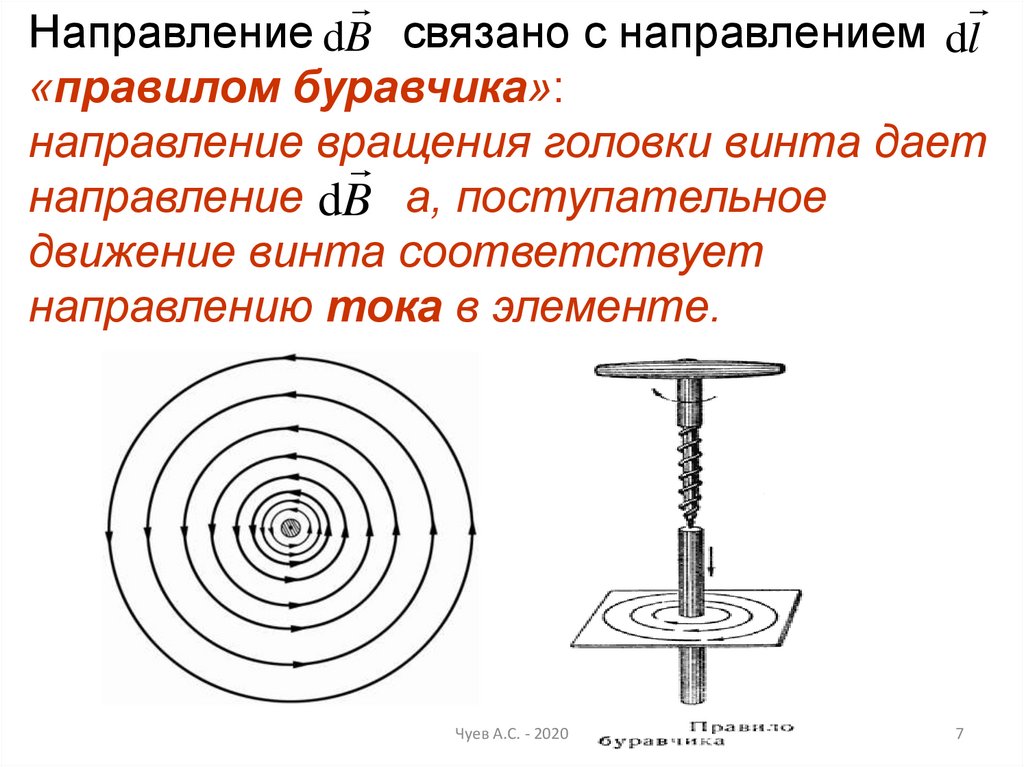
7.
Направление dB связано с направлением dl«правилом буравчика»:
направление вращения
головки винта дает
направление dB а, поступательное
движение винта соответствует
направлению тока в элементе.
Чуев А.С. - 2020
7
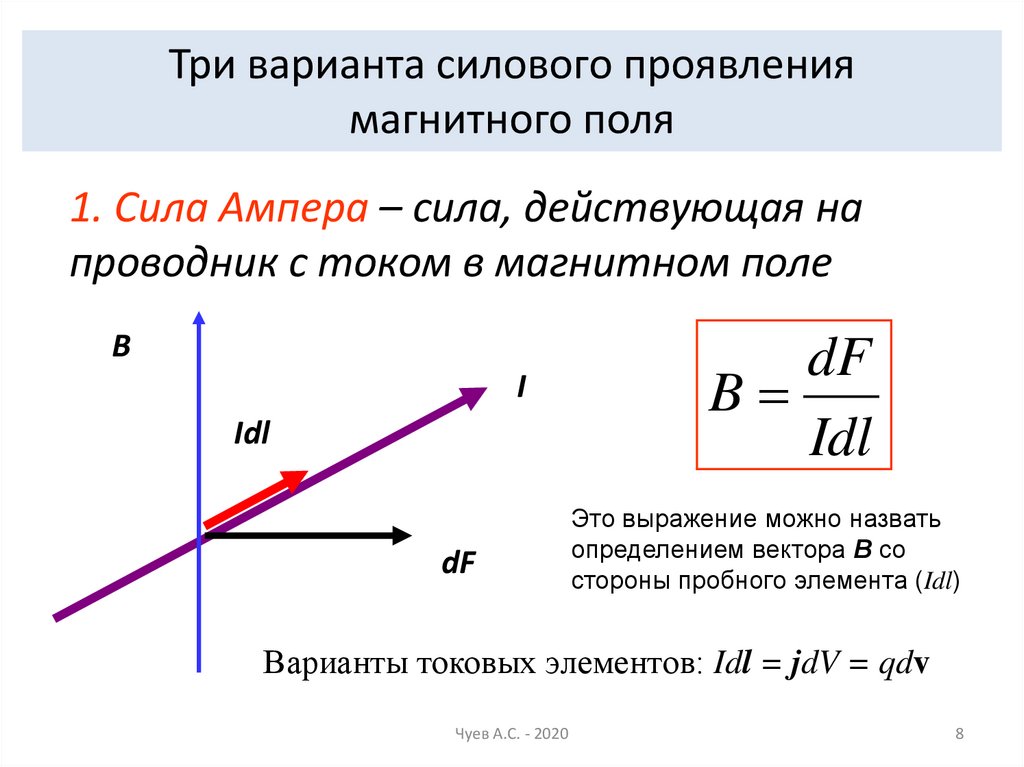
8.
Три варианта силового проявлениямагнитного поля
1. Сила Ампера – сила, действующая на
проводник с током в магнитном поле
B
I
Idl
dF
dF
B
Idl
Это выражение можно назвать
определением вектора В со
стороны пробного элемента (Idl)
Варианты токовых элементов: Idl = jdV = qdv
Чуев А.С. - 2020
8
9.
Для ограниченных по длинепроводников с токами
Для бесконечны по длине
проводников с токами
(Il)1(Il) 2
F 0
2 b 2
Чуев А.С. - 2020
9
10.
2. Сила ЛоренцаСила, действующая на электрический заряд
q во внешнем магнитном поле. Она
зависит от скорости его движения V и
величины индукции магнитного поля
В(x,y,z).
F = q[V,B].
Чуев А.С. - 2020
10
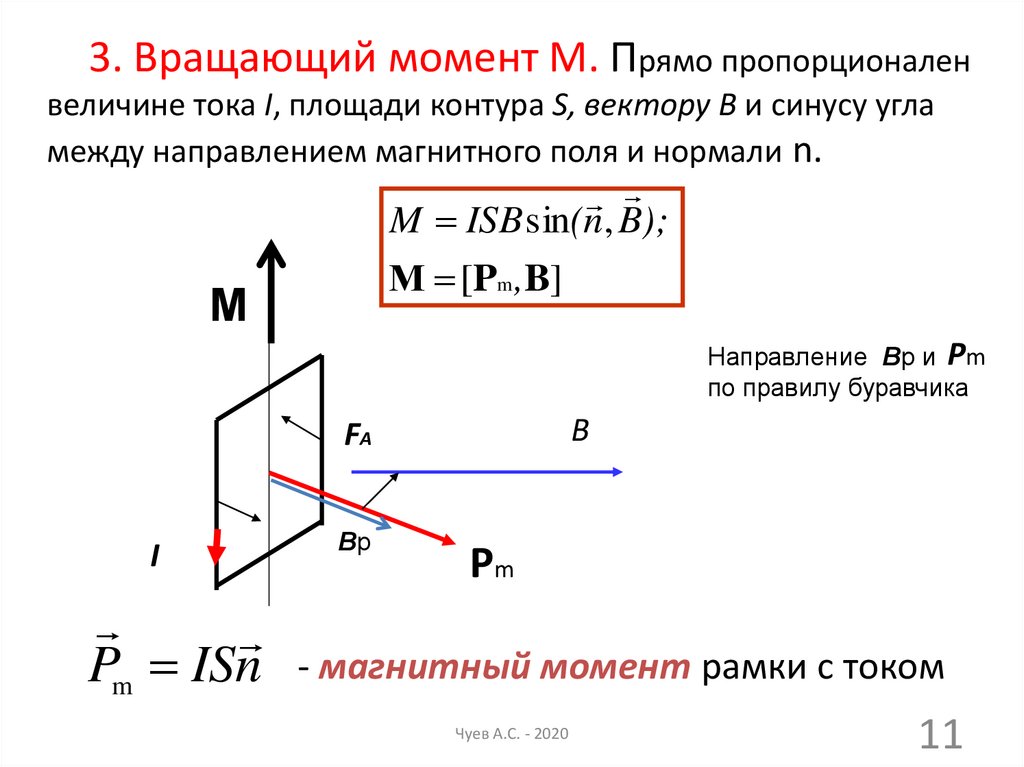
11.
3. Вращающий момент М. Прямо пропорционаленвеличине тока I, площади контура S, вектору В и синусу угла
между направлением магнитного поля и нормали n.
M ISB sin(n, B);
М [Pm ,B]
М
Направление Вр и Pm
по правилу буравчика
B
FA
I
Pm ISn
Вр
Pm
- магнитный момент рамки с током
Чуев А.С. - 2020
11
12.
Определение вектора магнитной индукциичерез момент силы
Отношение момента силы к магнитному моменту
B
M
Pm
для данной точки магнитного поля будет одним и
тем же и может служить характеристикой
магнитного поля, называемой магнитной
индукцией:
M
B
Pm sin( n, B)
M [ Pm , B]
Чуев А.С. - 2020
12
13.
Магнитный момент рамки (петли) с токомЧуев А.С. - 2020
13
14.
с пояснениямиЗакон Био-Савара-Лапласа
(Определение индукции В со стороны элемента, создающего поле)
0 dl , r I
0 Idl
dB
sin
или
dB
3
2
4
r
4 r
где: dB - магнитная индукция поля, создаваемого элементом
проводника dl с током I;
- радиус-вектор, проведенный от элемента проводника к
r
точке, в которой определяется магнитная индукция;
- угол между радиус-вектором и направлением тока в
элементе проводника;
dl - вектор, равный по модулю длине проводника и
совпадающий по направлению с током (элемент проводника).
Чуев А.С. - 2020
14
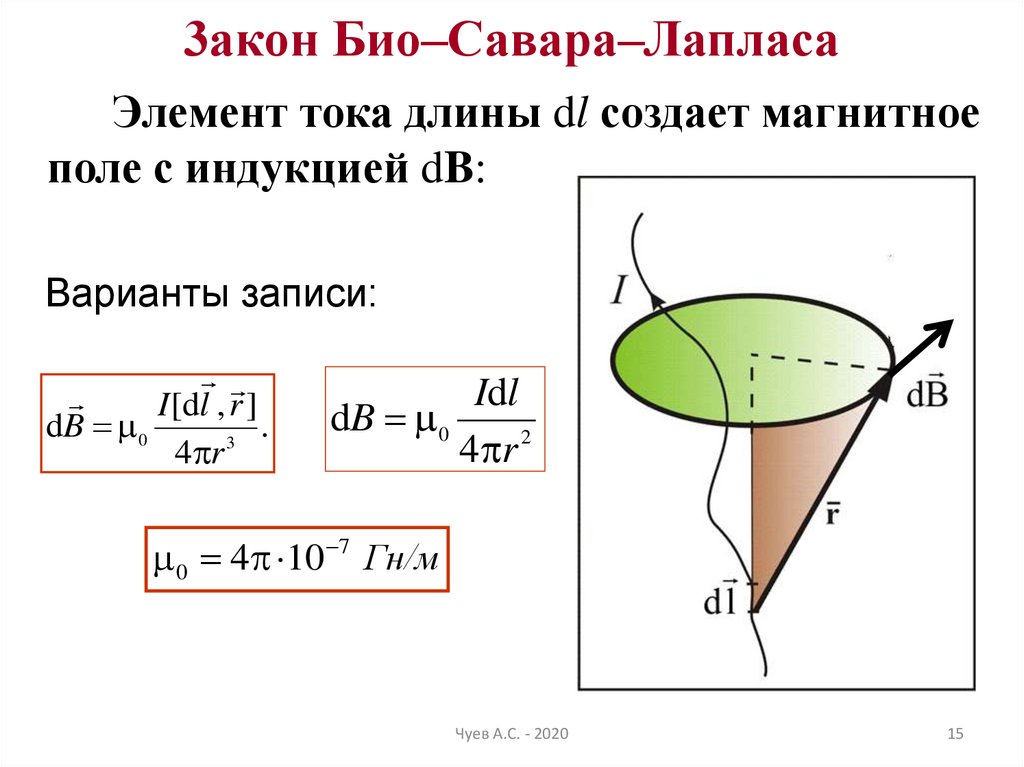
15. 3акон Био–Савара–Лапласа
Элемент тока длины dl создает магнитноеполе с индукцией dB:
Варианты записи:
I [dl , r ]
dB 0
.
3
4 r
Idl
dB 0
4 r 2
0 4 10 7 Гн/м
Чуев А.С. - 2020
15
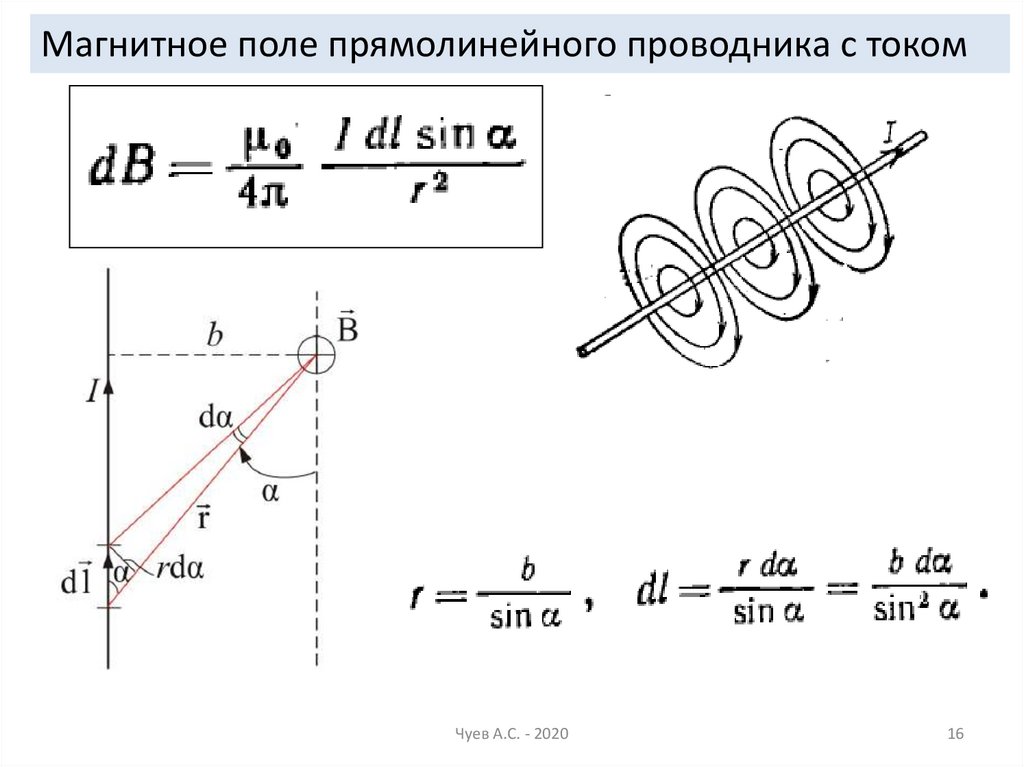
16.
Магнитное поле прямолинейного проводника с токомЧуев А.С. - 2020
16
17.
Конечная формула для индукции, создаваемойпрямым длинным проводником с током
Чуев А.С. - 2020
17
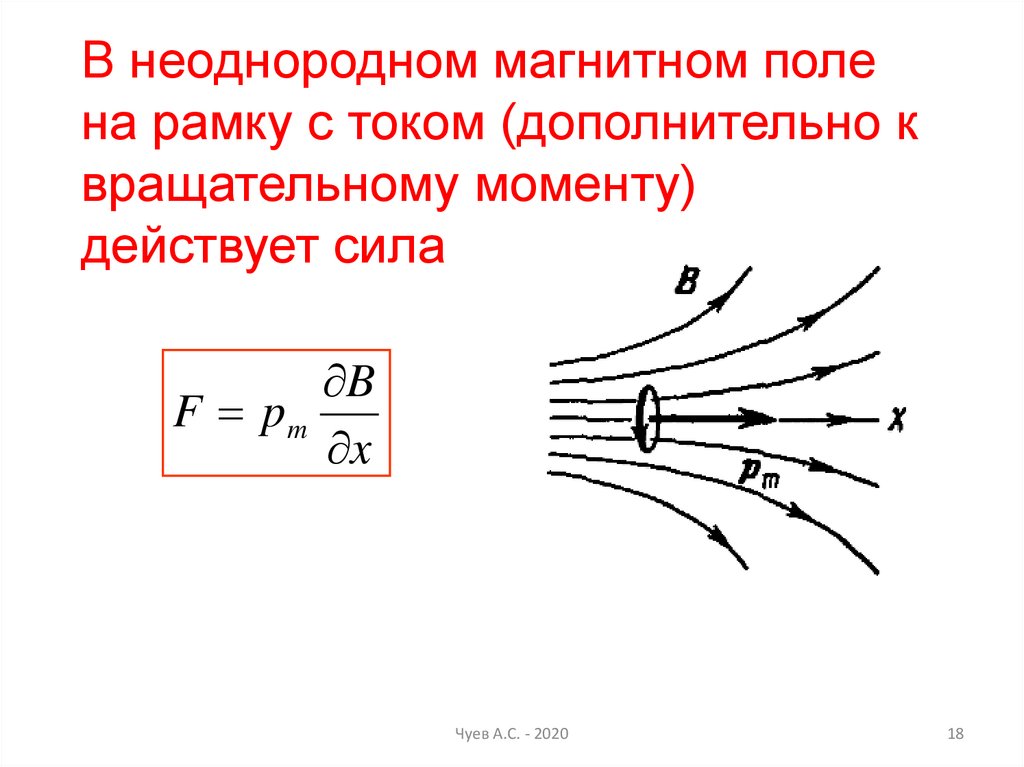
18.
В неоднородном магнитном полена рамку с током (дополнительно к
вращательному моменту)
действует сила
B
F pm
x
Чуев А.С. - 2020
18
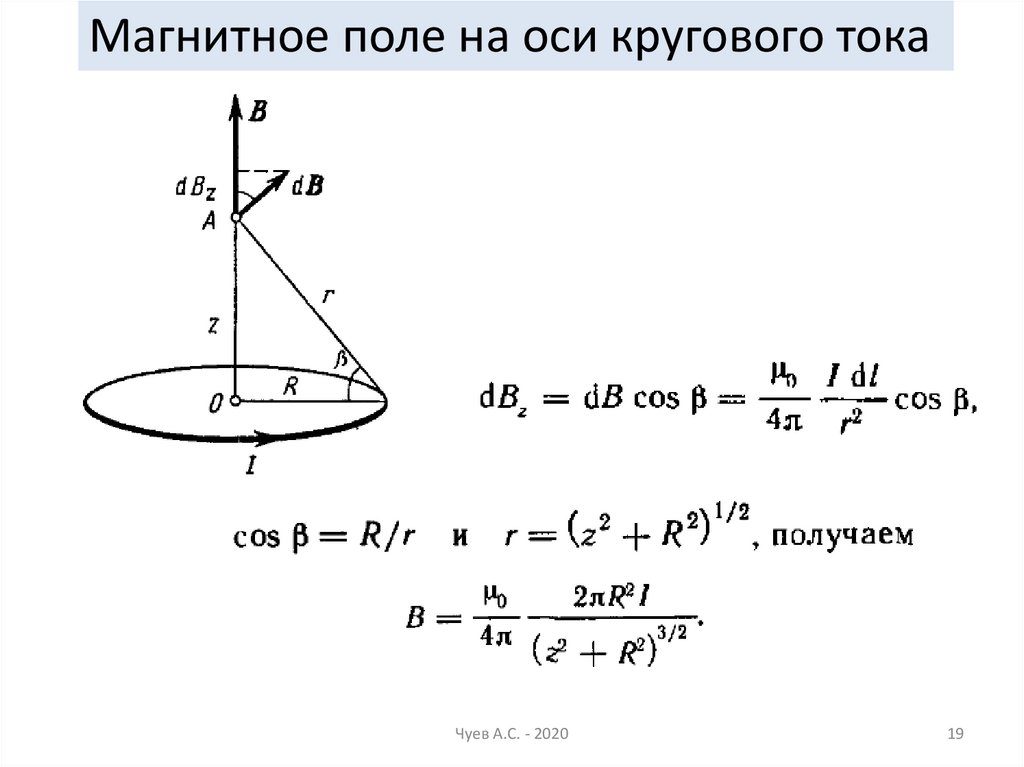
19.
Магнитное поле на оси кругового токаЧуев А.С. - 2020
19
20.
ПОТОК ВЕКТОРА МАГНИТНОЙИНДУКЦИИ
Поток Ф любой векторной величиныA
через площадку S математически
определяется как интеграл:
Ф AdS
S
Математически поток всегда скаляр, физически – это векторная
величина
Чуев А.С. - 2020
20
21.
ПОТОК МАГНИТНОЙ ИНДУКЦИИФ B n dS.
S
dФ B B d S cos ( d n , B )
Принято:
Ф BdS
S
Следовало бы
Ф BdS n .
S
Чуев А.С. - 2020
21
22.
Возможное определение единицымагнитной индукции через поток:
1 Тл равен магнитной индукции
при которой магнитный поток
сквозь площадку 1 м2,
перпендикулярную направлению
поля, равен 1 Вб.
Чуев А.С. - 2020
22
23.
ТЕОРЕМА ГАУССА ДЛЯ ВЕКТОРАМАГНИТНОЙ ИНДУКЦИИ
Поскольку магнитных зарядов нет, то считается:
B
d
S
0
S
Интегральная
форма
div B 0
Дифференциальная
форма
Чуев А.С. - 2020
23
24.
Теорема о циркуляции вектора магнитнойиндукции в интегральной и дифференциальной
формах (для вакуума!!)
B
d
l
I
0
rotB 0 j
Чуев А.С. - 2020
24
25.
Определение ротораЧуев А.С. - 2020
25
26.
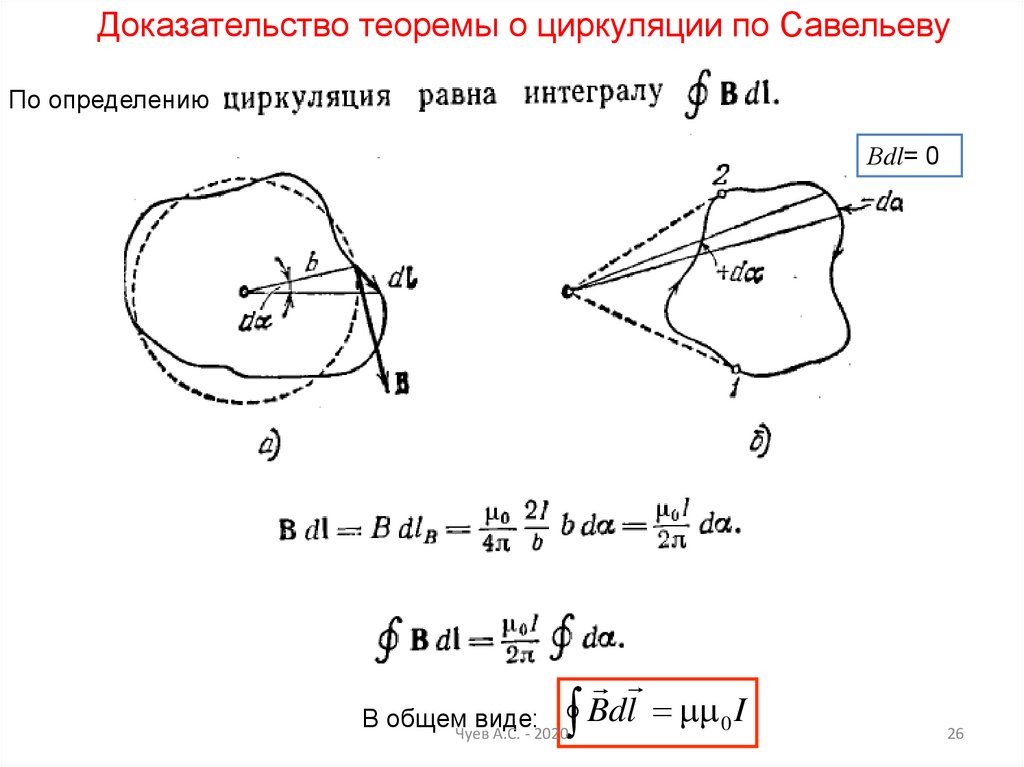
Доказательство теоремы о циркуляции по СавельевуПо определению
Вdl= 0
Bdl 0 I
В общемЧуев
виде:
А.С. - 2020
26
27.
Доказательство теоремы о циркуляции в дифференциальной формеЧуев А.С. - 2020
27
28.
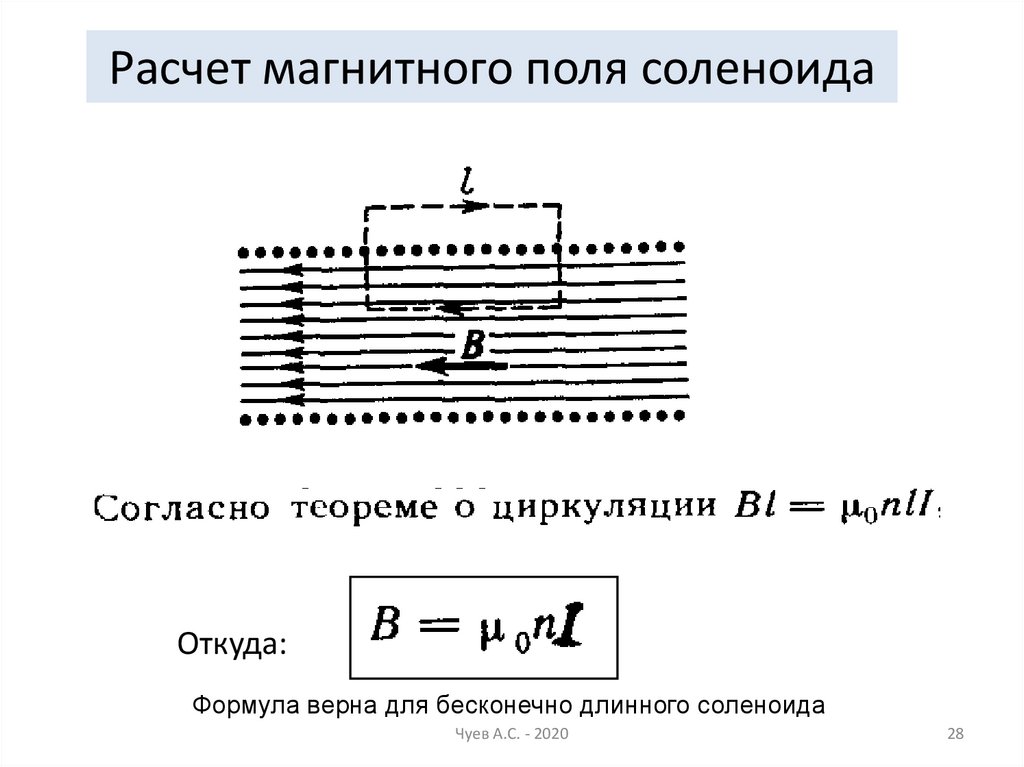
Расчет магнитного поля соленоидаОткуда:
Формула верна для бесконечно длинного соленоида
Чуев А.С. - 2020
28
29.
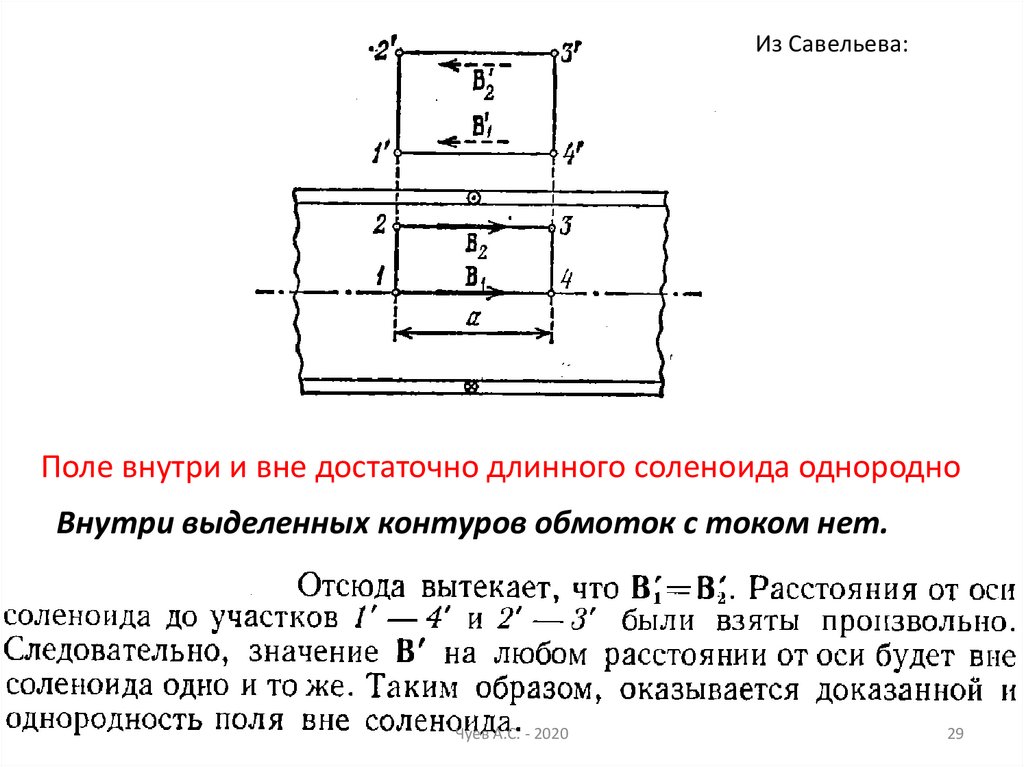
Из Савельева:Поле внутри и вне достаточно длинного соленоида однородно
Внутри выделенных контуров обмоток с током нет.
Чуев А.С. - 2020
29
30.
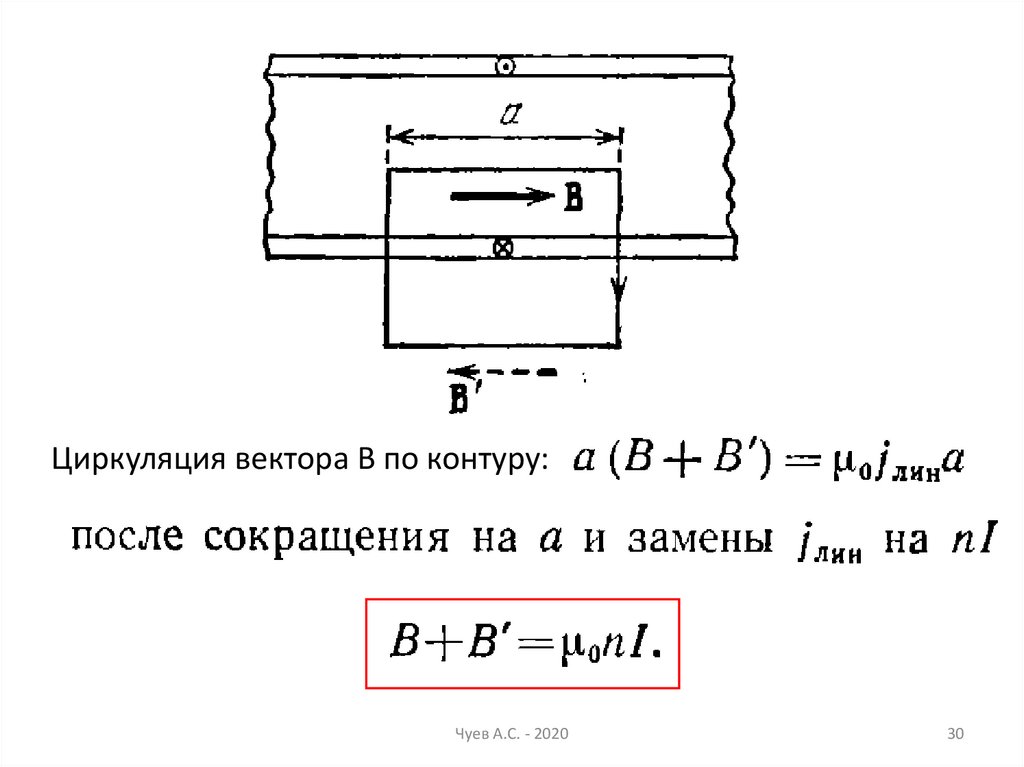
Циркуляция вектора В по контуру:Чуев А.С. - 2020
30
31.
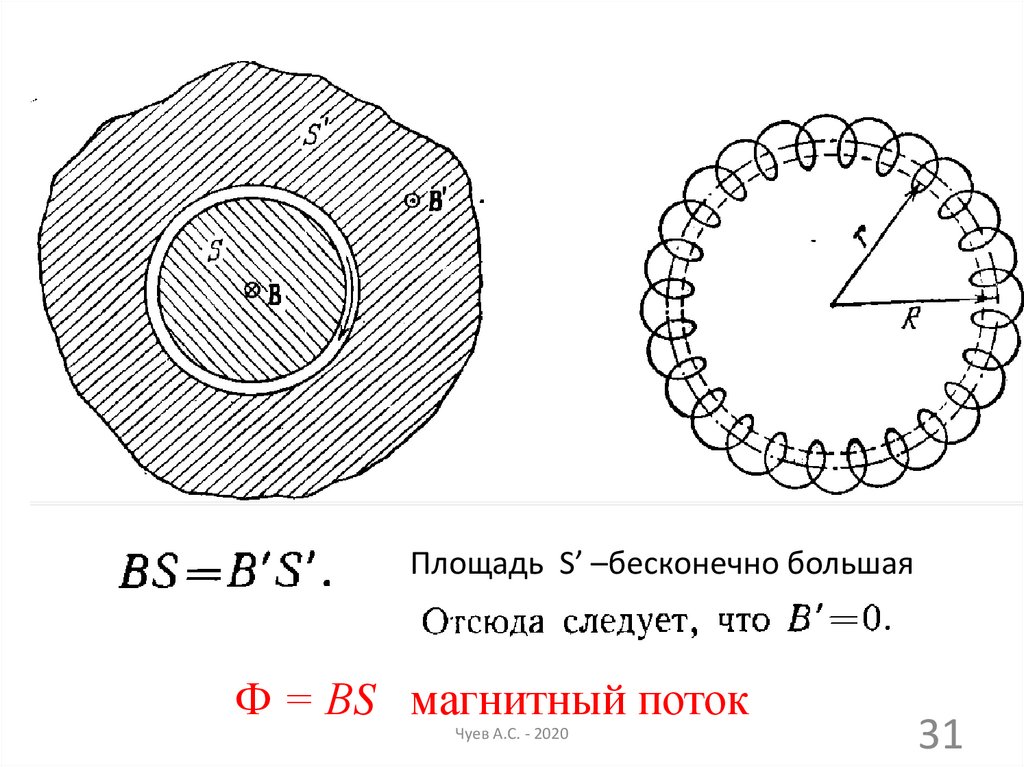
Площадь S’ –бесконечно большаяФ = ВS магнитный поток
Чуев А.С. - 2020
31
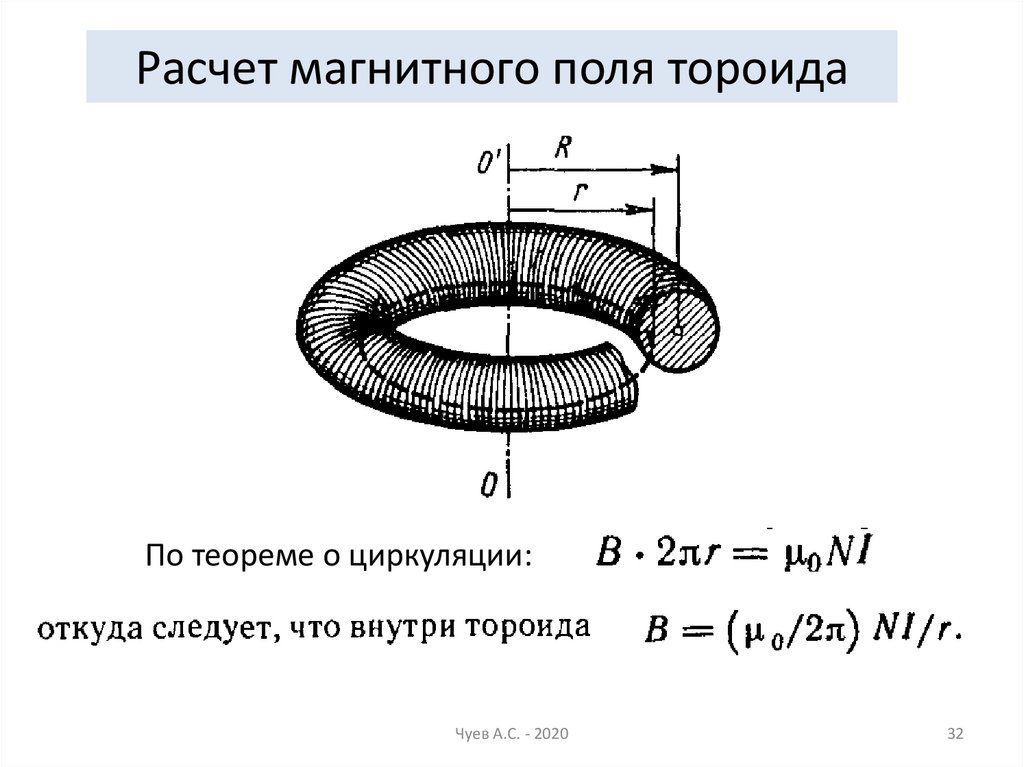
32.
Расчет магнитного поля тороидаПо теореме о циркуляции:
Чуев А.С. - 2020
32
33. Магнитный поток и индуктивность
c учетом Hdl=∑IL 0 n 2V
Чуев А.С. - 2020
33
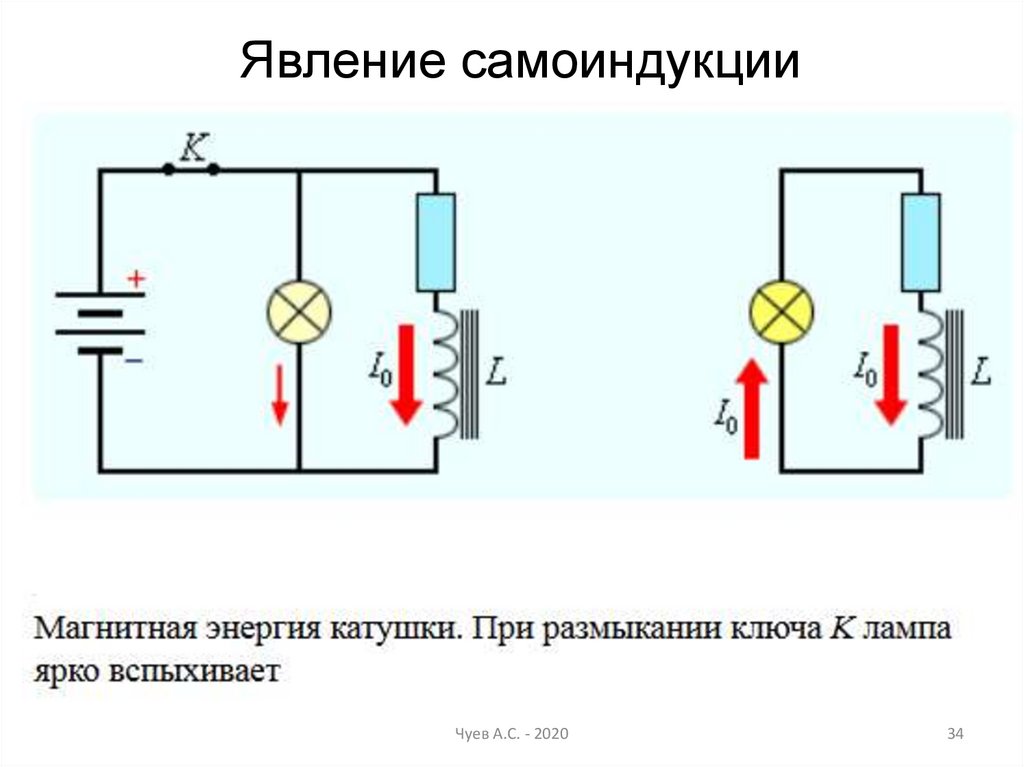
34.
Явление самоиндукцииЧуев А.С. - 2020
34
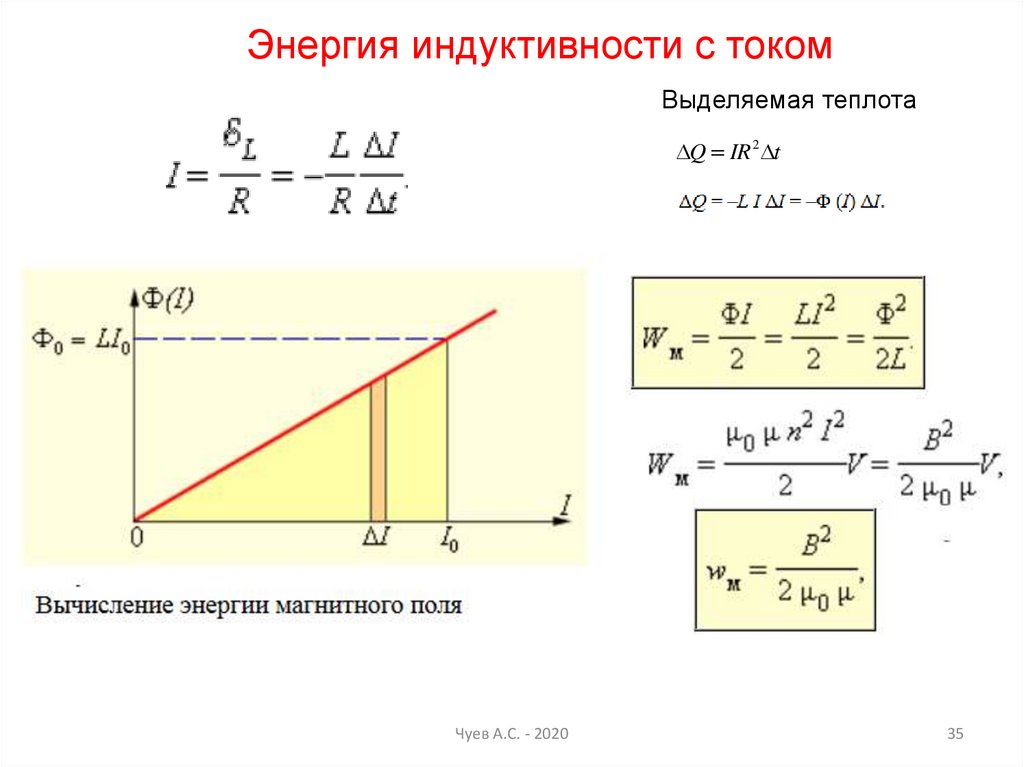
35.
Энергия индуктивности с токомВыделяемая теплота
Q IR 2 t
Чуев А.С. - 2020
35
36.
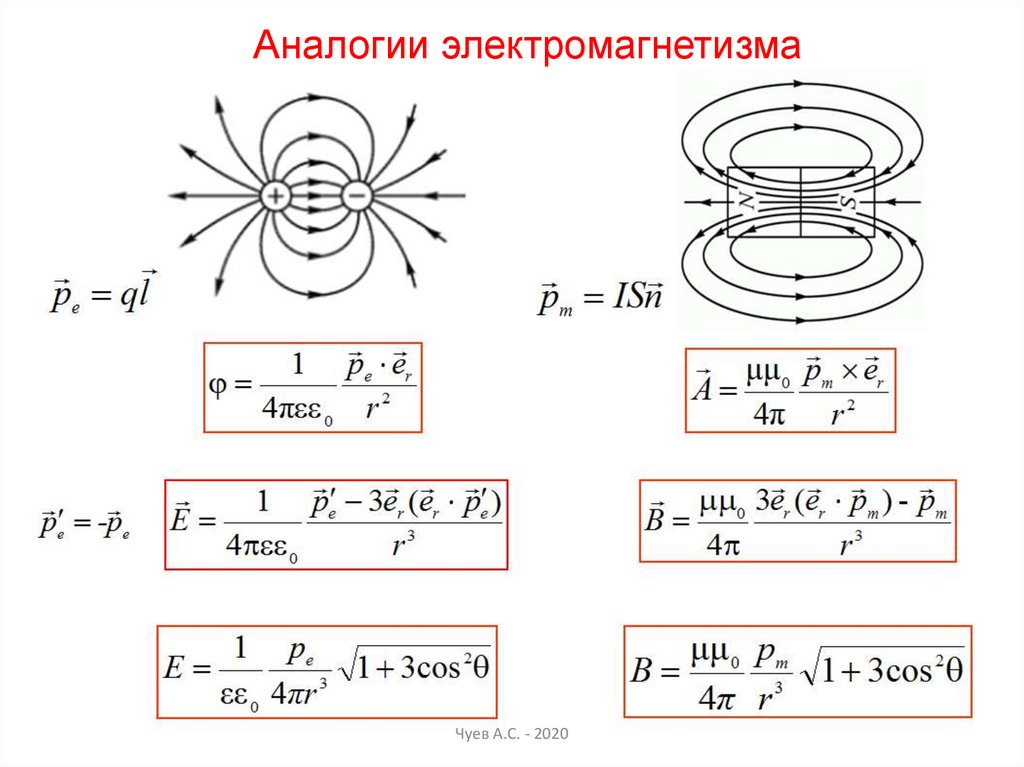
Аналогии электромагнетизмаЧуев А.С. - 2020
36
37.
Чуев А.С. - 202037
38.
Чуев А.С. - 202038
39.
Вектор напряженности магнитногополя Н
Термин напряженность появился первым,
затем ввели понятие магнитной индукции,
обозначив ее буквой В
B 0 H
Для вакуума B 0 H
В системе СГС магнитная индукция считается макроскопическим полем, а
напряженность микроскопическим (атомно-молекулярным) магнитным
полем, т.е., по сути, различий нет.
Чуев А.С. - 2020
39
40.
Из этого выражения, используя теорему СтоксаУчитывая, что:
I j dS
Hdl rotHdS
Г
S
Получим:
S
rotH j
Чуев А.С. - 2020
40
41.
Теорема о циркуляции вектора HС учетом:
Можно записать:
Чуев А.С. - 2020
41
42.
Теорема о циркуляции векторанапряженности магнитного поля в
интегральной и дифференциальной формах
(формулы верны всегда)
H
d
l
I
rotH j
Чуев А.С. - 2020
42
43.
преобразуем вЧуев А.С. - 2020
43
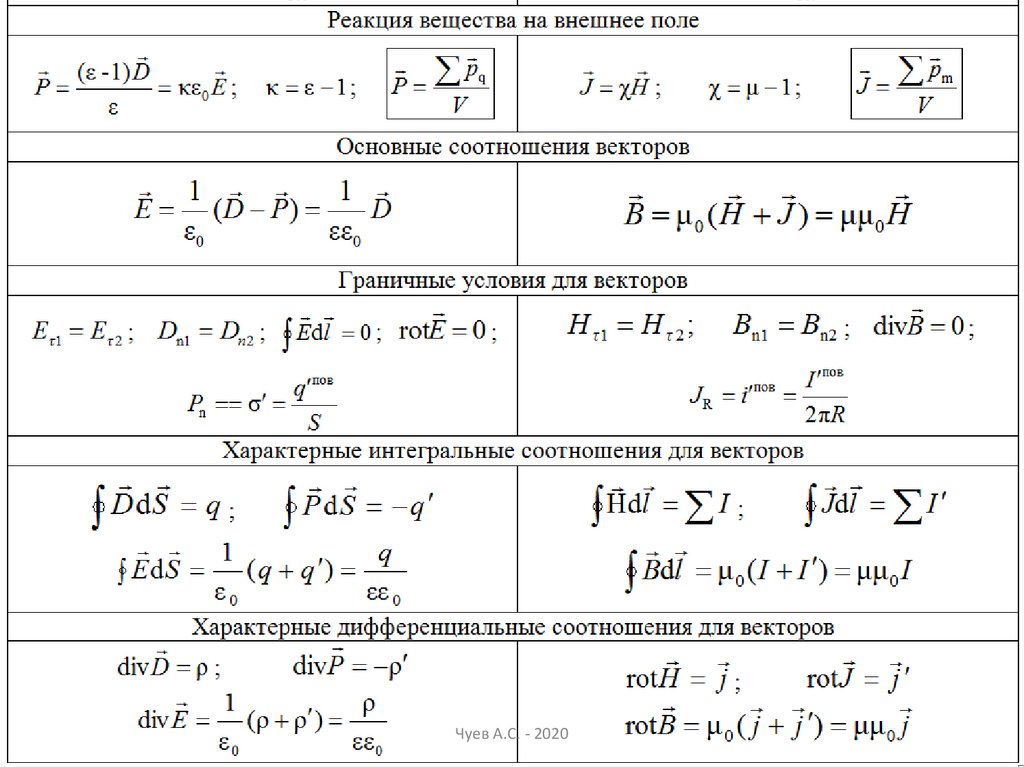
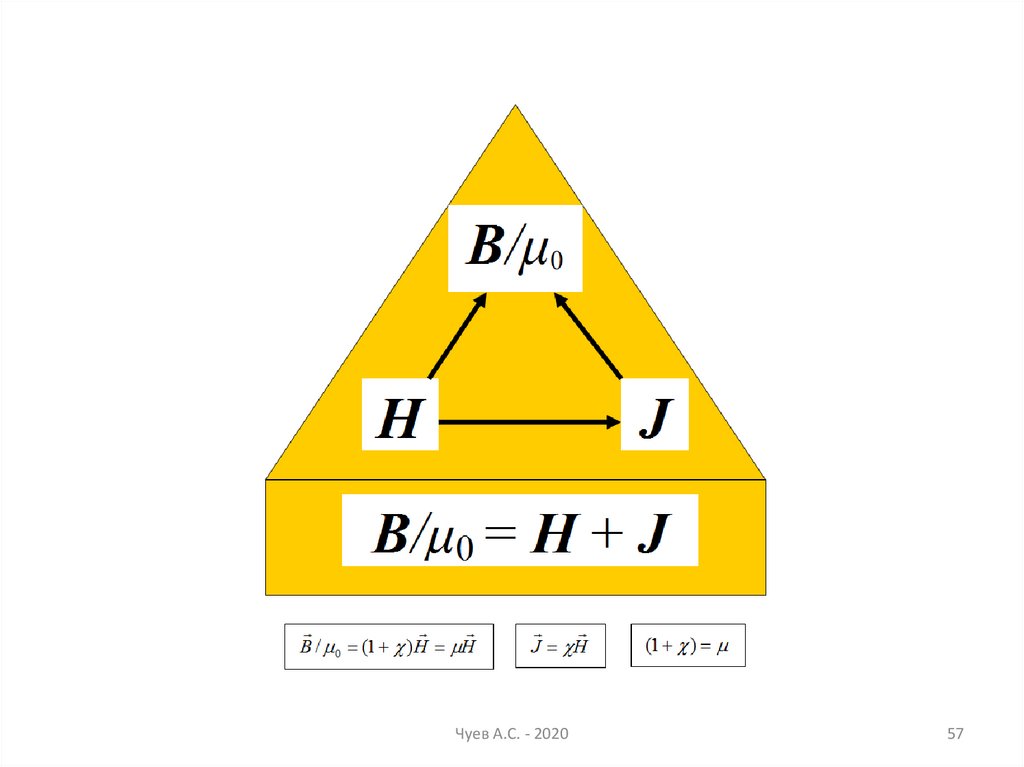
44. Соотношения для вектора намагниченности
Чуев А.С. - 202044
45.
Вектор В суммарный полевой векторB 0 H 0 ( Н J )
rotB 0 j 0 ( j j )
Аддитивность интегральной и дифференциальной
функций подтверждает правильность первой формулы
Чуев А.С. - 2020
45
46.
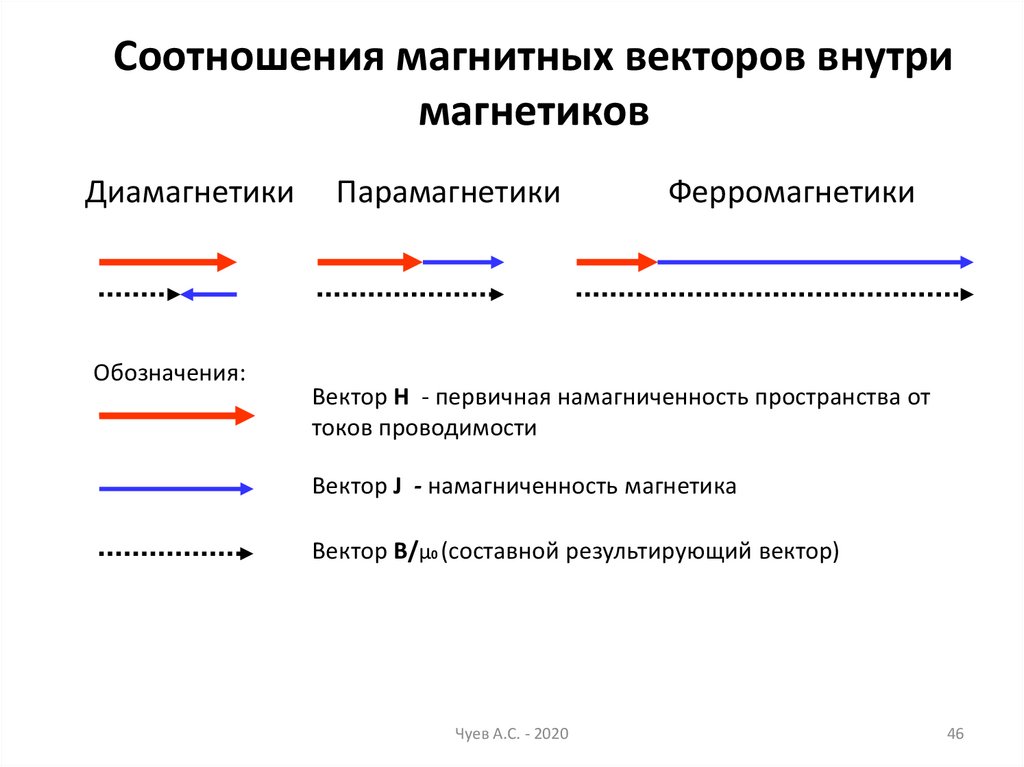
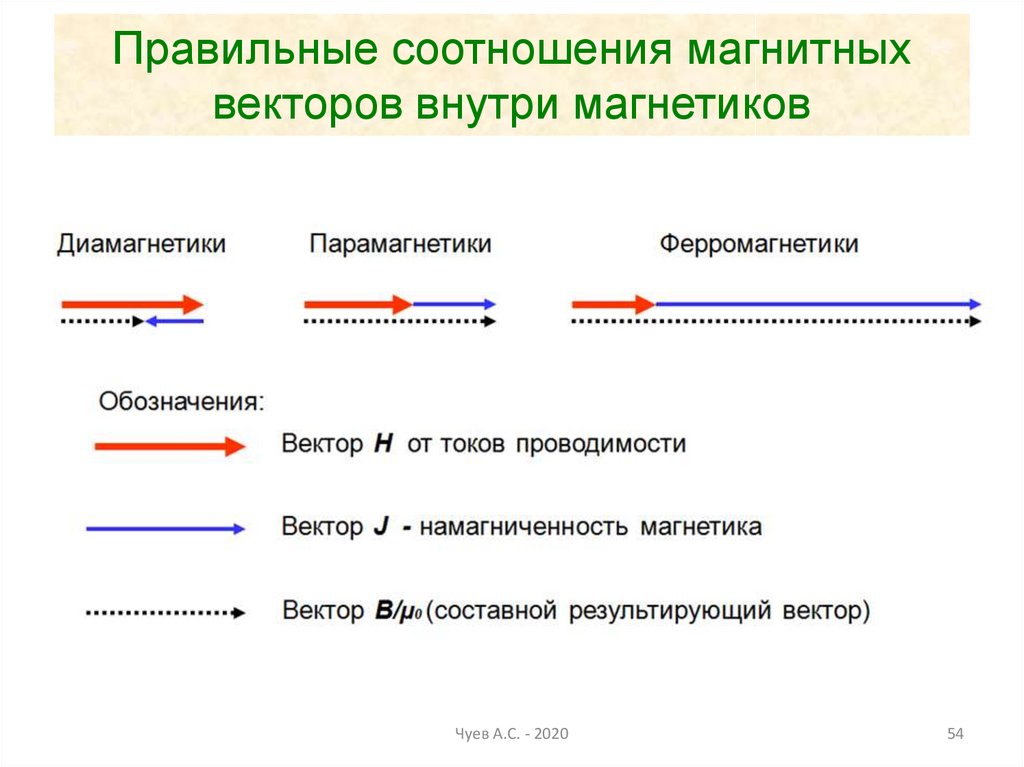
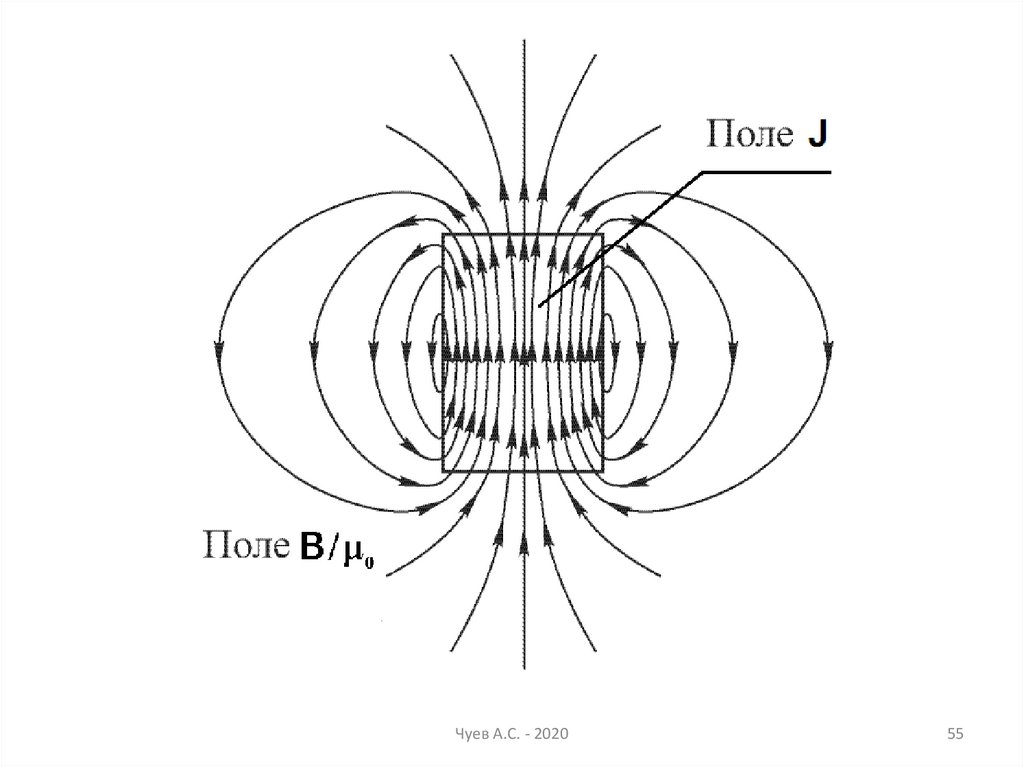
Соотношения магнитных векторов внутримагнетиков
Диамагнетики
Обозначения:
Парамагнетики
Ферромагнетики
Вектор H - первичная намагниченность пространства от
токов проводимости
Вектор J - намагниченность магнетика
Вектор B/µ0 (составной результирующий вектор)
Чуев А.С. - 2020
46
47.
Пример из ДЗЧуев А.С. - 2020
47
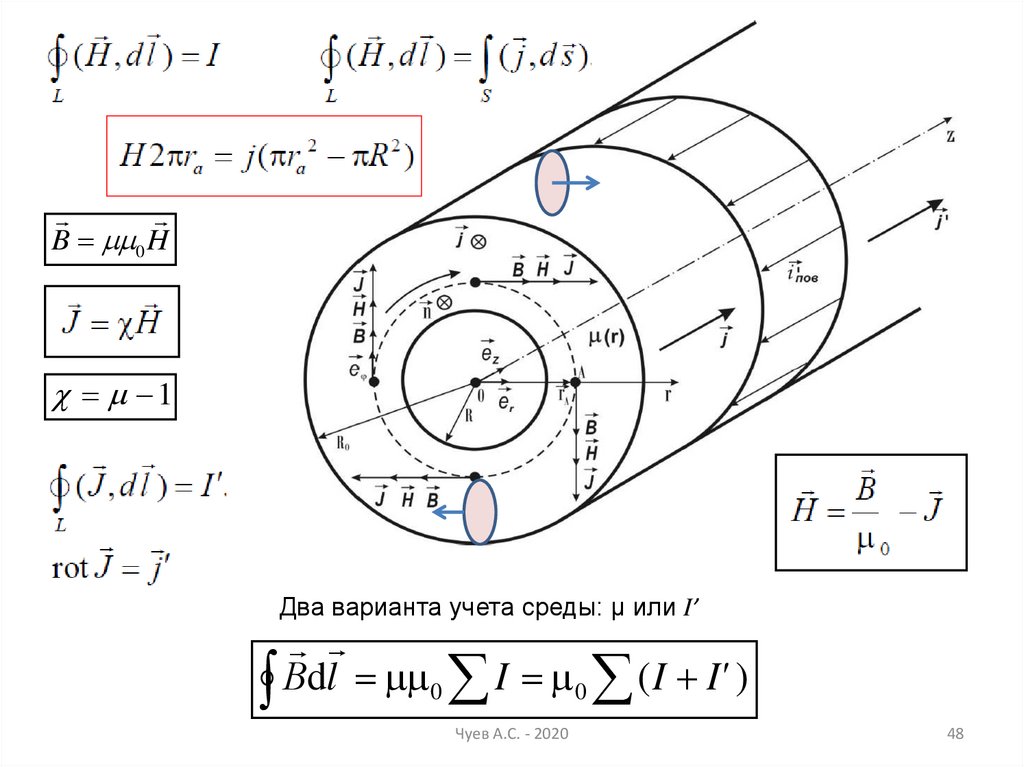
48.
B 0 H1
Два варианта учета среды: µ или I’
Вdl 0 I 0 ( I I' )
Чуев А.С. - 2020
48
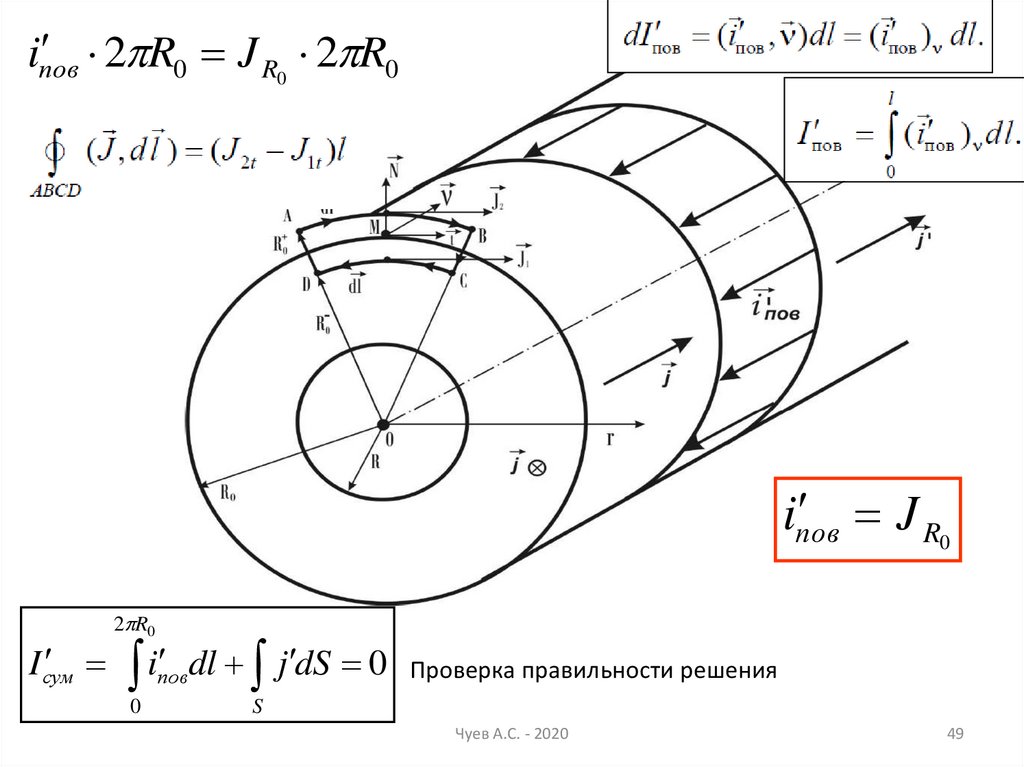
49.
2 R0 J R0 2 R0iпов
J R0
iпов
I сум
2 R0
i
пов
0
dl j dS 0
Проверка правильности решения
S
Чуев А.С. - 2020
49
50.
ФАКУЛЬТАТИВНЫЙМАТЕРИАЛ ЛЕКЦИИ
Чуев А.С. - 2020
50
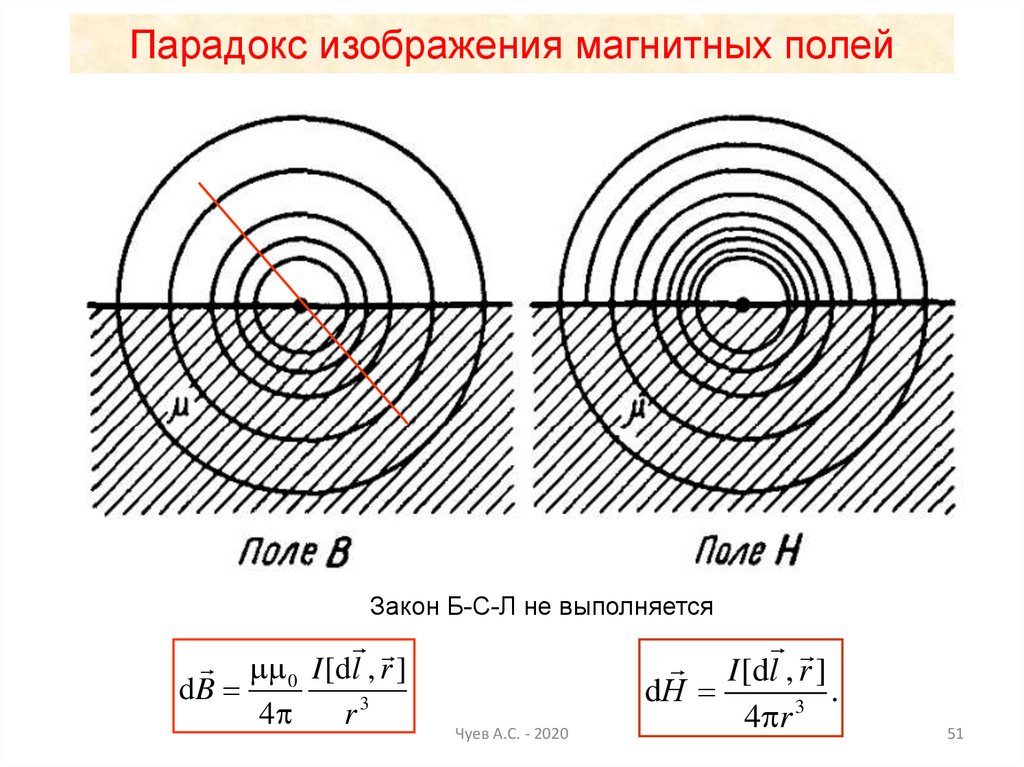
51.
Парадокс изображения магнитных полейЗакон Б-С-Л не выполняется
0 I [dl , r ]
dB
4
r3
Чуев А.С. - 2020
I [dl , r ]
dН
.
3
4 r
51
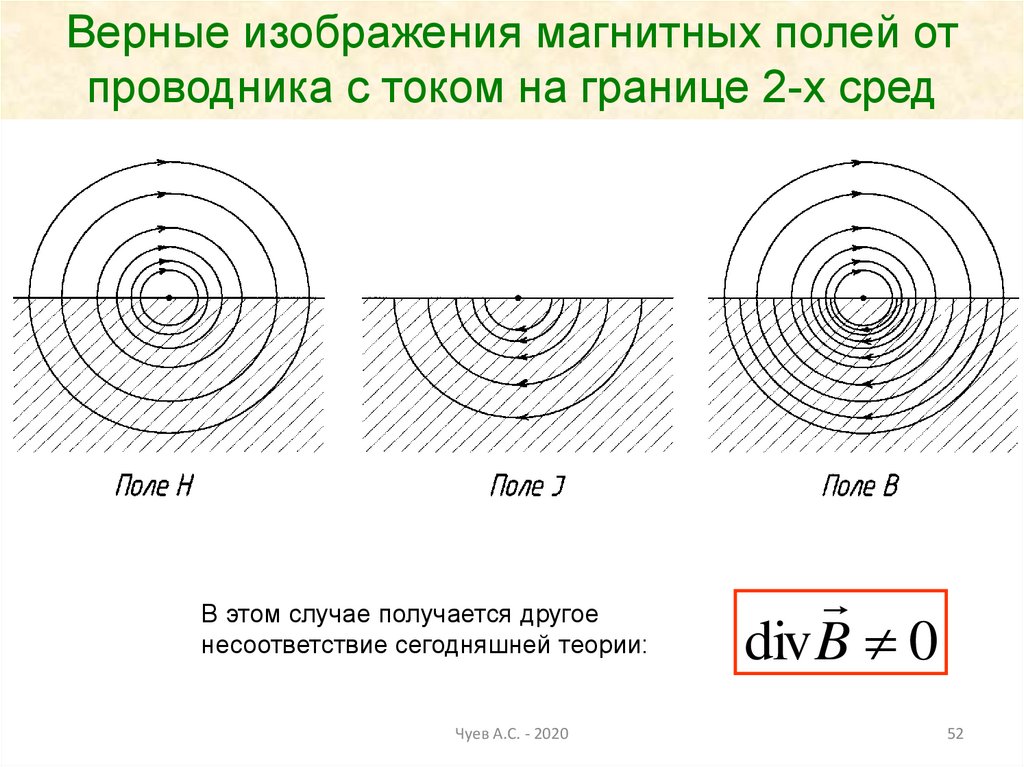
52.
Верные изображения магнитных полей отпроводника с током на границе 2-х сред
В этом случае получается другое
несоответствие сегодняшней теории:
Чуев А.С. - 2020
div B 0
52
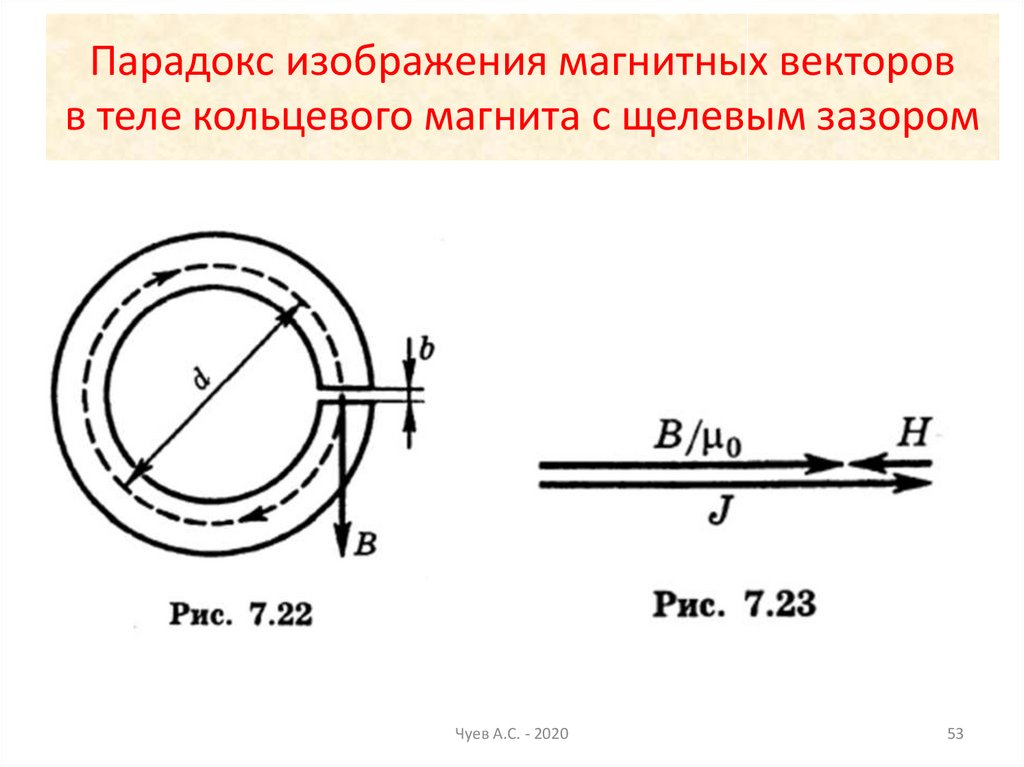
53. Парадокс изображения магнитных векторов в теле кольцевого магнита с щелевым зазором
Чуев А.С. - 202053
54.
Правильные соотношения магнитныхвекторов внутри магнетиков
Чуев А.С. - 2020
54
55.
Чуев А.С. - 202055
56.
Чуев А.С. - 202056
57.
Чуев А.С. - 202057
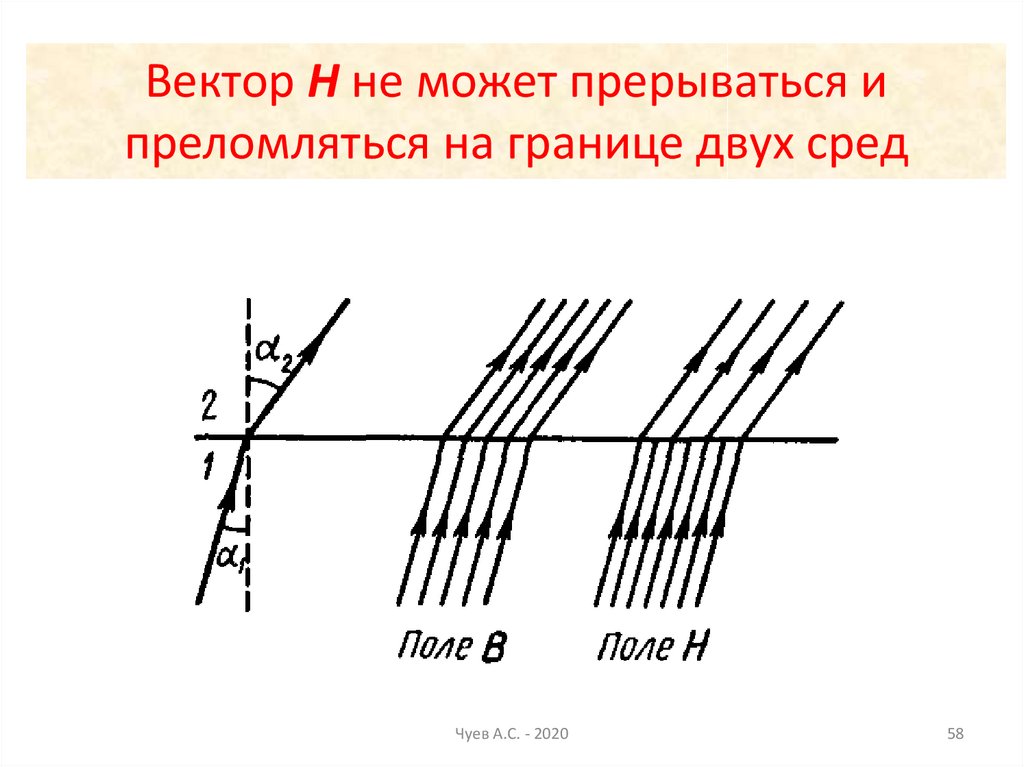
58.
Вектор Н не может прерываться ипреломляться на границе двух сред
Чуев А.С. - 2020
58
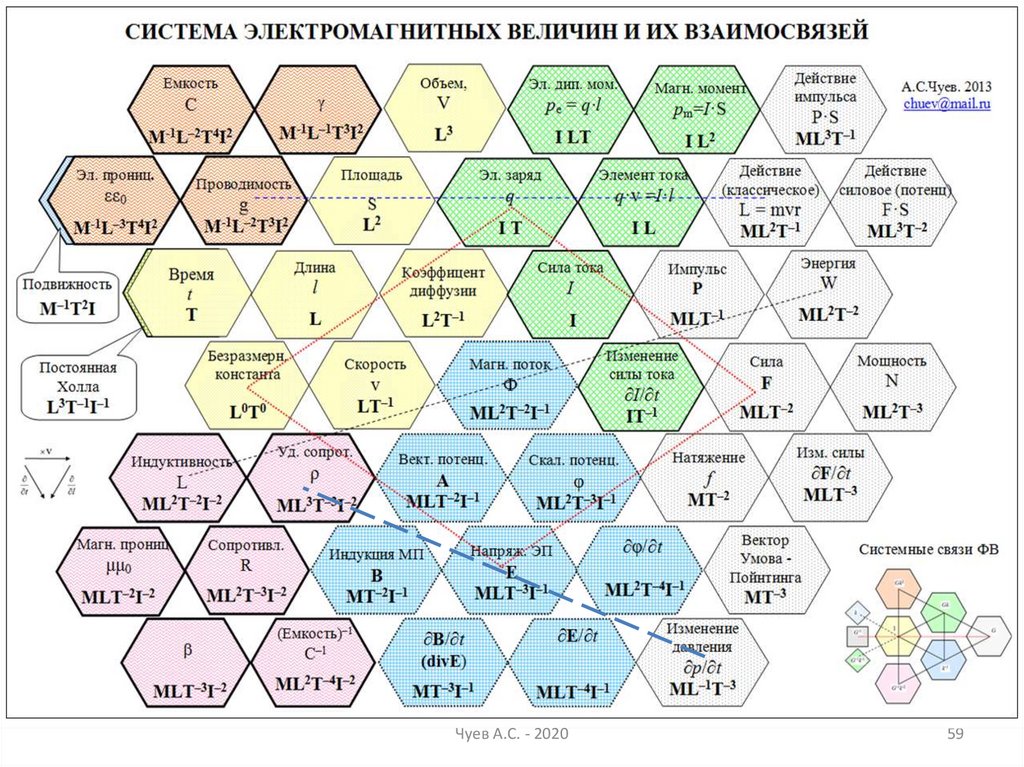
59.
Чуев А.С. - 202059
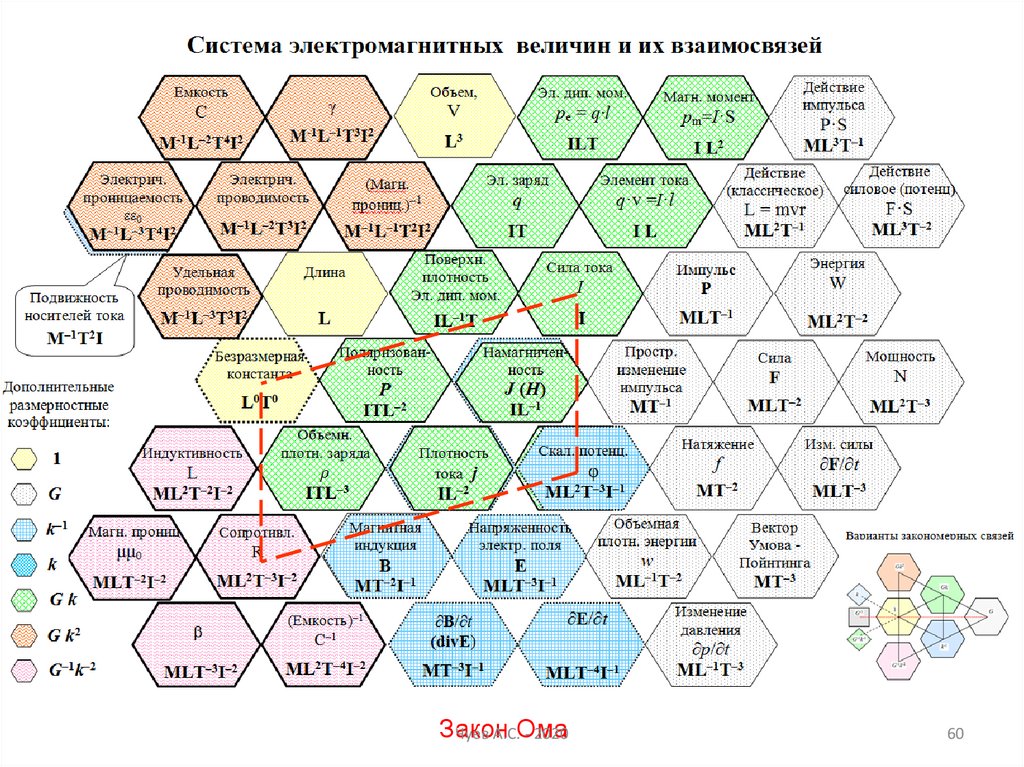
60.
ЗаконЧуев А.С.Ома
- 2020
60
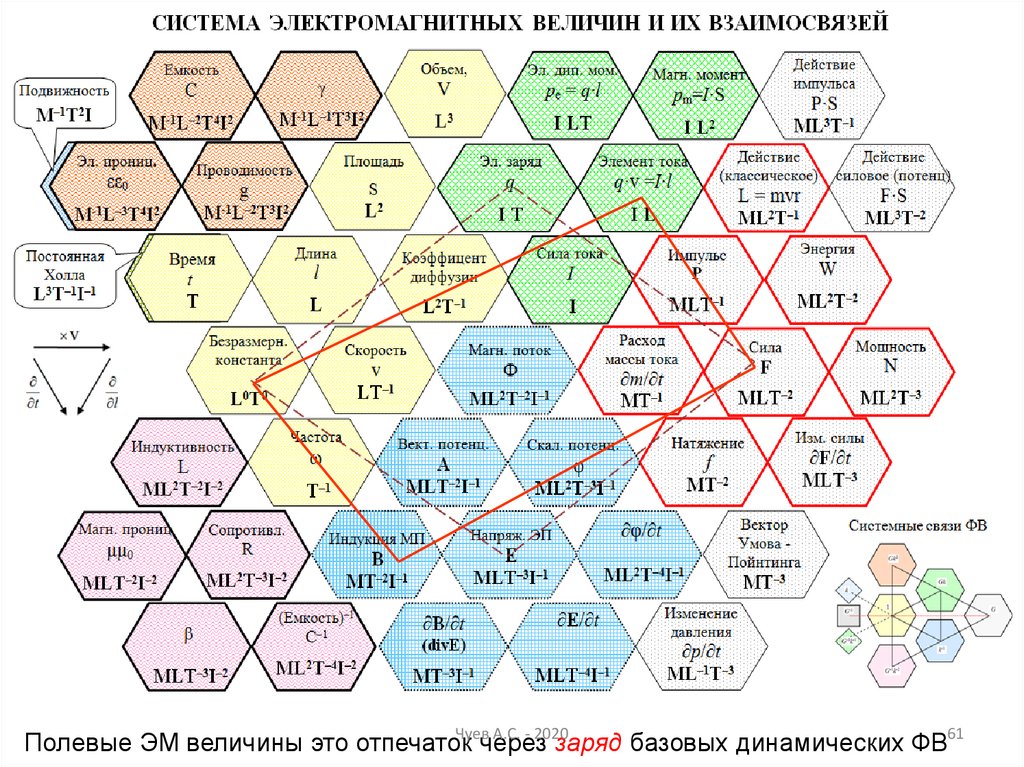
61.
Чуев А.С. - 2020Полевые ЭМ величины это отпечаток
через заряд базовых динамических ФВ61
62.
Чуев А.С. - 202062
63.
Чуев А.С. - 202063
64.
КОНЕЦ ПРЕЗЕНТАЦИИЧуев А.С. - 2020
64































 physics
physics








