Similar presentations:
Магнитное поле в вакууме
1.
Магнитное поле в вакууме2.
Магнитные явления были известны еще вдревнем мире. Компас был изобретен более
4500 лет тому назад.
Он появился в Европе приблизительно в
XII веке новой эры. Однако только в XIX веке
была обнаружена связь между электричеством и
магнетизмом и возникло представление о
магнитном поле. Первыми экспериментами,
показавшими, что между электрическими и
магнитными явлениями имеется глубокая связь,
были опыты датского физика Х. Эрстеда
(1820 г.).
Эти опыты показали, что на магнитную
стрелку, расположенную вблизи
проводника с током, действуют силы,
которые стремятся повернуть стрелку.
3.
• Силовое взаимодействие электрических токовЭксперимент, проведенный Ампером в 1820 г., показал, что
проводники с токами взаимодействуют между собой с силой (из
расчета на единицу длины каждого из параллельных проводников)
пропорциональной
величинам
токов
в
них
и
обратно
пропорциональной расстоянию между ними, т. е.
F k
ед
2 I I
b
1
2
где коэффициент пропорциональности в системе СИ .
Причем одинаково направленные токи – притягиваются,
а противоположно направленные – отталкиваются (см.
рис.). Сейчас это выражение рассматривается как одна
из форм закона Ампера.
4.
Объяснение силового взаимодействия токов (или направленныхпотоков заряженных частиц): осуществляется через особое поле,
сосредоточенное в пространстве и названное магнитным полем.
Название «магнитное поле» появилось в 1820 г. после того, как
Эрстед
экспериментально
установил
ориентирующее
действие
проводника с током на магнитную стрелку компаса. В опыте Эрстеда
провод (с током) располагался над магнитной стрелкой, и при
включении тока I – стрелка устанавливалась перпендикулярно к
проводу с током (см. рис.).
Таким образом, магнитное поле
имеет
направленный
характер
и
должно характеризоваться векторной
величиной.
I
S'
Bпр
S
N'
Bстр N
5.
Источниками магнитного поля являются движущиеся электрические заряды(токи). Магнитное поле возникает в пространстве, окружающем проводники
с током, подобно тому, как в пространстве, окружающем неподвижные
электрические заряды, возникает электрическое поле. Магнитное поле
постоянных магнитов также создается электрическими микротоками,
циркулирующими внутри молекул вещества (гипотеза Ампера). В результате
обобщения экспериментальных данных был получен элементарный закон,
определяющий поле В точечного заряда q, движущегося с постоянной
нерелятивистской скоростью v. Этот закон записывается в виде:
0 q vr
B
4 r 3
μ0 – магнитная постоянная.
0
10 7 Гн/м
4
6.
BМагнитная индукция
характеризует силовое
действие магнитного поля на ток (аналогично,
E
характеризует силовое действие электрического поля на
заряд).
B – силовая характеристика магнитного поля, ее
можно изобразить с помощью магнитных силовых
линий.
7.
Для вектора индукции магнитного поля В справедливпринцип суперпозиции:
– магнитная индукция результирующего поля равна
векторной сумме магнитных индукций Вi складываемых
полей
n
B Bi
i 1
или в случае непрерывного проводника
B d B
L
8.
В пространстве вокруг проводника с током возникает
вихревое магнитное поле.
Индукция магнитного поля dB элементарного отрезка
dl с током I на расстоянии r от него определяется законом
Био – Савара – Лапласа :
0 I d l, r
dB
4 r 3
или по модулю
0 Idl
dB
2
4 r
где 0 = 4 10 7 Гн/м = 1,25663706144 10 6 Гн/м–
магнитная постоянная, определяемая выбором системы
единиц.
9.
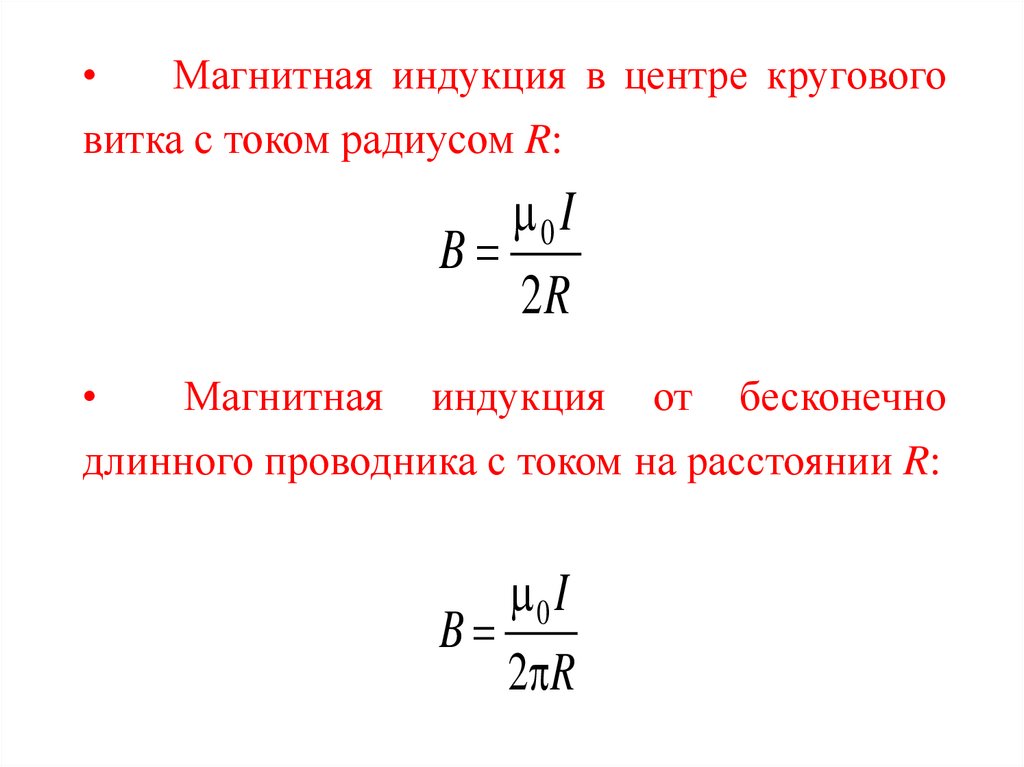
Магнитная индукция в центре кругового
витка с током радиусом R:
0 I
B
2R
Магнитная
индукция
от
бесконечно
длинного проводника с током на расстоянии R:
0 I
B
2 R
10.
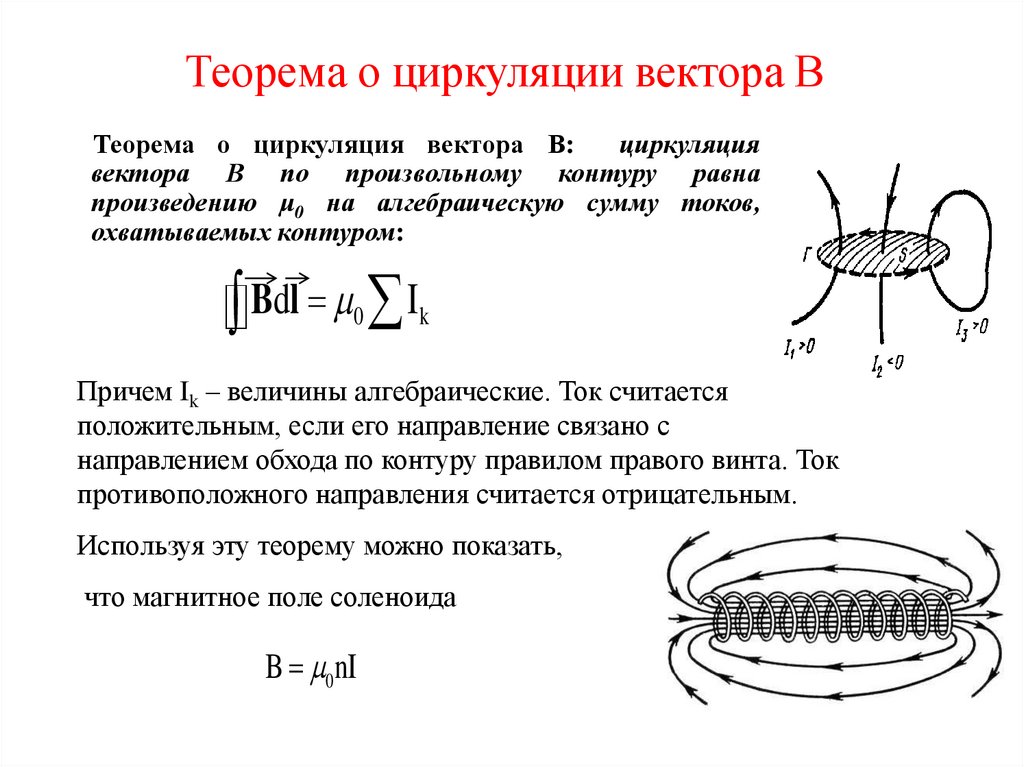
Теорема о циркуляции вектора ВТеорема о циркуляция вектора В:
циркуляция
вектора В по произвольному контуру равна
произведению μ0 на алгебраическую сумму токов,
охватываемых контуром:
Bdl I
0
k
Причем Ik – величины алгебраические. Ток считается
положительным, если его направление связано с
направлением обхода по контуру правилом правого винта. Ток
противоположного направления считается отрицательным.
Используя эту теорему можно показать,
что магнитное поле соленоида
B 0nI
11.
Закон АмпераАМПЕР Андре Мари (1775 –
1836) – французский физик
математик и химик.
Основные
физические
работы
посвящены
электродинамике.
Сформулировал правило для
определения
действия
магнитного поля тока на
магнитную
стрелку.
Обнаружил влияние магнитного
поля Земли на движущиеся
проводники с током.
12.
В 1820 г. А. М. Ампер экспериментальноустановил, что два проводника с током
взаимодействуют друг с другом с силой:
I1 I 2
F k
b
где b – расстояние между проводниками, а k – коэффициент
пропорциональности зависящий от системы единиц.
В первоначальное выражение закона
Ампера не входила никакая величина
характеризующая магнитное поле. Потом
разобрались, что взаимодействие токов
осуществляется через магнитное поле и
следовательно в закон должна входить
характеристика магнитного поля.
13.
В современной записи в системе СИ,закон Ампера выражается формулой:
dF I [ d l , B ]
Это сила с которой магнитное поле
действует на бесконечно малый проводник с
током I.
Модуль силы действующей на проводник
dF IBdlsin d l ,B .
14.
Направление силы определяется направлением векторногопроизведения или правилом левой руки (что одно и тоже).
Ориентируем пальцы по направлению первого вектора,
второй вектор должен входить в ладонь и большой палец
показывает направление векторного произведения.
Закон Ампера –
это первое
открытие
фундаментальн
ых сил,
зависящих от
скоростей.
15.
16.
Из закона Ампера хорошо виден физический смыслмагнитной индукции: В – величина, численно равная силе,
с которой магнитное поле действует на проводник
единичной длины, по которому течет единичный ток.
B
F
Il
Размерность индукции
Н
B 1Тл.
А м
17.
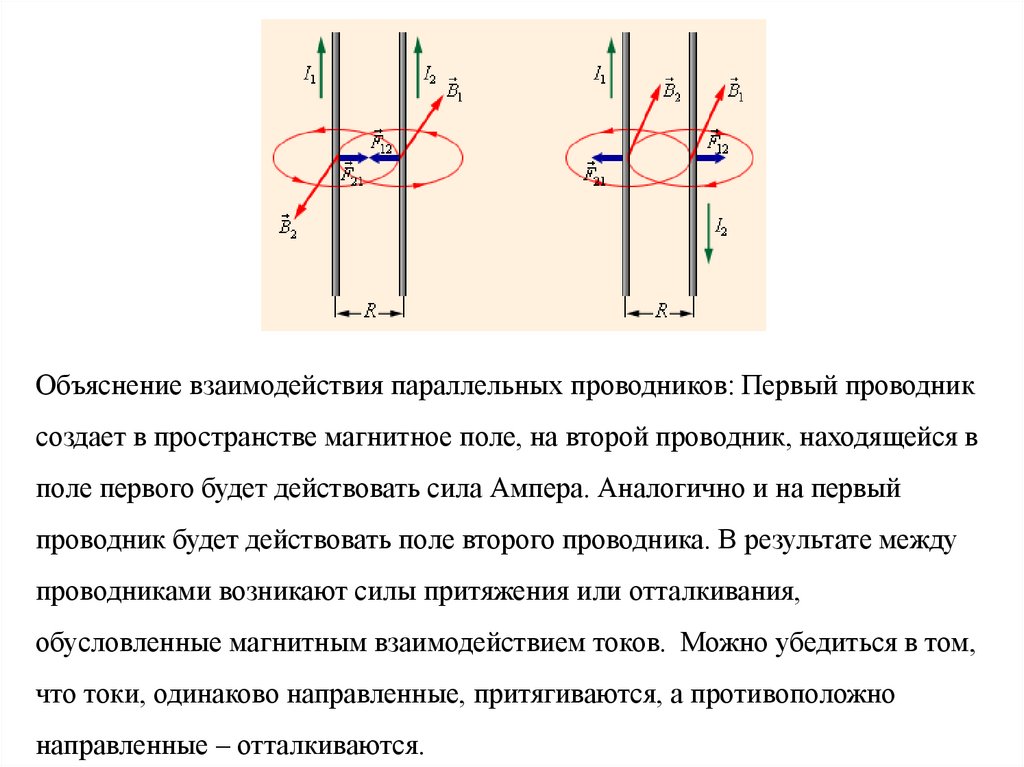
Объяснение взаимодействия параллельных проводников: Первый проводниксоздает в пространстве магнитное поле, на второй проводник, находящейся в
поле первого будет действовать сила Ампера. Аналогично и на первый
проводник будет действовать поле второго проводника. В результате между
проводниками возникают силы притяжения или отталкивания,
обусловленные магнитным взаимодействием токов. Можно убедиться в том,
что токи, одинаково направленные, притягиваются, а противоположно
направленные – отталкиваются.
18.
Поведение элементарного контура с током удобно описывать спомощью магнитного момента pm. По определению
pm ISn
Подробный расчет по формуле
F I dl, B
с учетом малости контура приводи к следующему выражению для силы,
действующей на элементарный контур с током в неоднородном магнитном
поле:
B
F pm
n
B
– производная вектора В по направлению нормали n или по
n
направлению вектора p .
m
19.
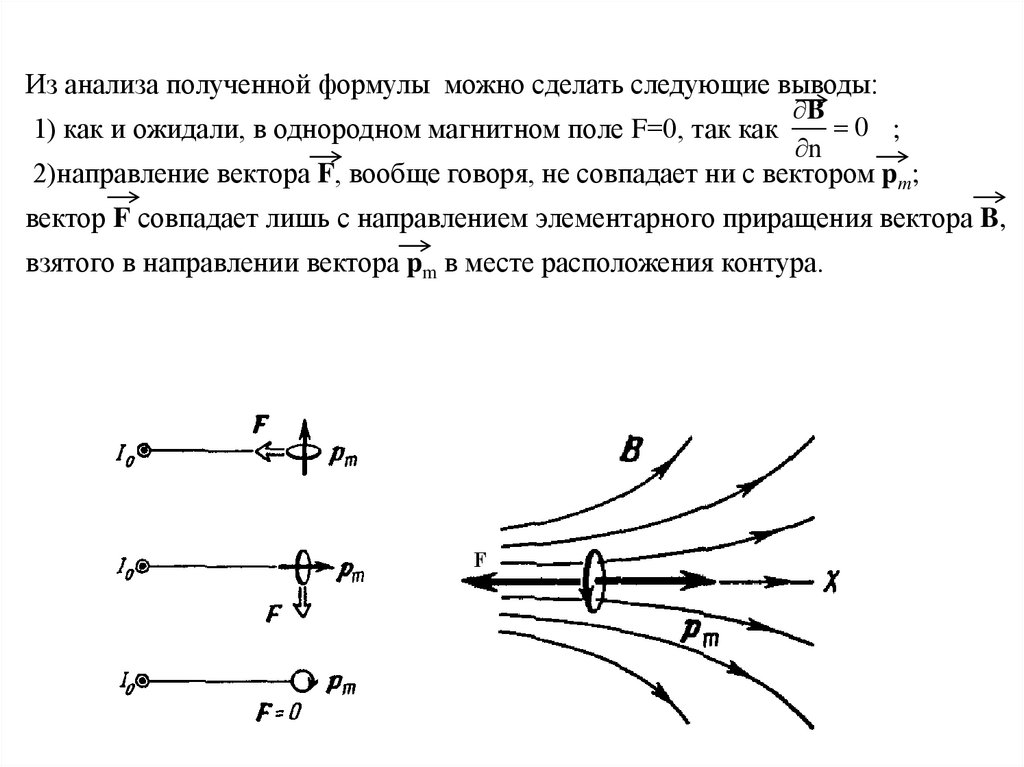
Из анализа полученной формулы можно сделать следующие выводы:B
0 ;
1) как и ожидали, в однородном магнитном поле F=0, так как
n
2)направление вектора F, вообще говоря, не совпадает ни с вектором pm;
вектор F совпадает лишь с направлением элементарного приращения вектора B,
взятого в направлении вектора pm в месте расположения контура.
20.
Сила ЛоренцаСила, действующая на электрический заряд q во
внешнем электромагнитном поле, зависит не только от его
местоположения и напряженности электрического поля
E(x,y,z) в этой точке: qE(x,y,z), но, в общем случае, и от
скорости его движения v и величины индукции
магнитного поля В(x,y,z).
Выражение для этой силы было получено в конце XIX
в. голландским физиком Г.А. Лоренцем
21.
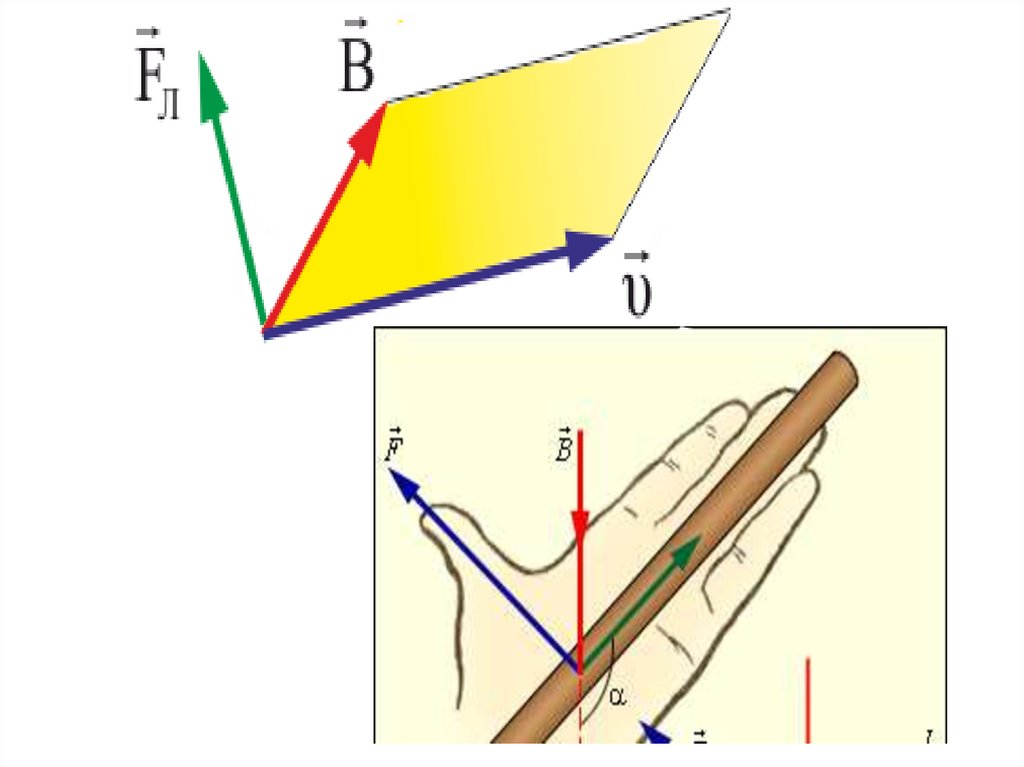
• Модуль лоренцевой силы:,
л
• где α – угол между B и υ .
• Из формулы
видно, что на заряд, движущийся вдоль
линии B , не действует сила ( sin 0 0 ).
Направлена сила Лоренца перпендикулярно
к
плоскости, в которой лежат векторы B и υ . К
движущемуся положительному заряду применимо
правило левой руки или «правило буравчика»
F q B sin
Fл q[ , B]
22.
23.
Если заряженная частица движется в однородном магнитном поле поддействием силы Лоренца, а ее скорость v лежит в плоскости,
перпендикулярной вектору B то частица будет двигаться по окружности
радиуса
mv
R=
qB
Сила Лоренца в этом случае играет роль
центростремительной силы. Период обращения частицы в
однородном магнитном поле равен
2 R 2 m
T
v
qB
Это выражение показывает, что для заряженных частиц заданной массы m
период обращения не зависит от скорости v и радиуса траектории R. Угловая
скорость движения заряженной частицы по круговой траектории:
2 qB
T
m
Называется циклотронной
частотой.
24.
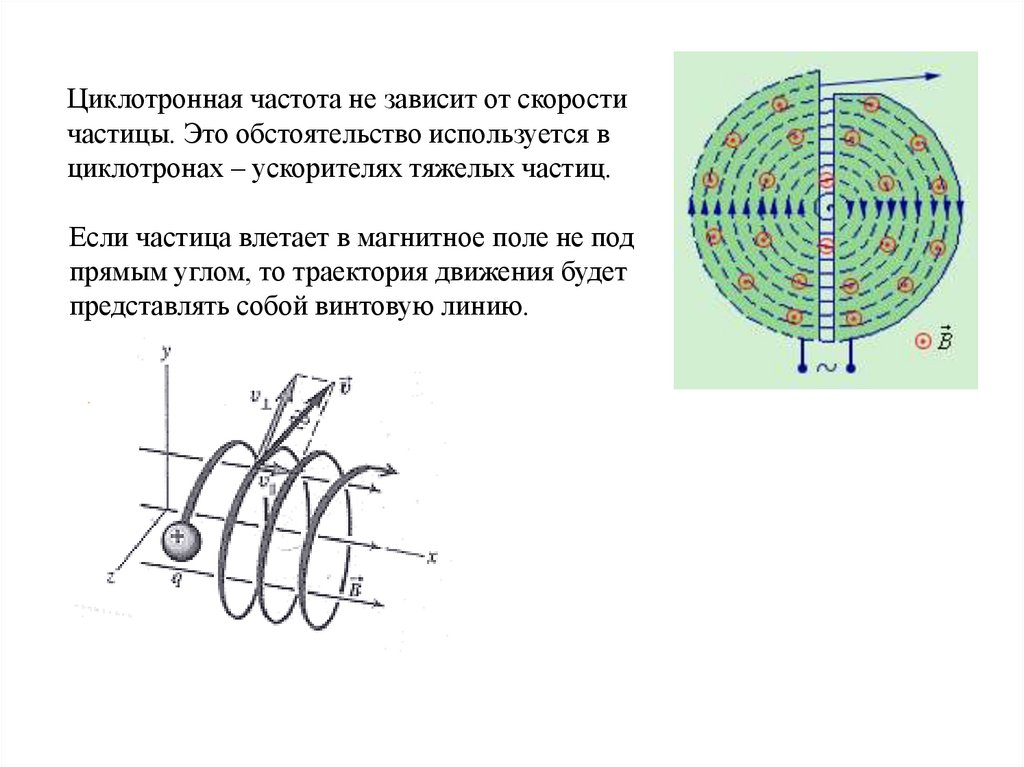
Циклотронная частота не зависит от скоростичастицы. Это обстоятельство используется в
циклотронах – ускорителях тяжелых частиц.
Если частица влетает в магнитное поле не под
прямым углом, то траектория движения будет
представлять собой винтовую линию.
25.
• Направлениедействия
силы
для
отрицательного заряда – противоположно,
следовательно, к электронам применимо
правило правой руки.
• Так
как
сила
Лоренца
направлена
перпендикулярно движущемуся заряду, т.е.
перпендикулярно , работа этой силы всегда
равна нулю. Следовательно, действуя на
заряженную частицу, сила Лоренца не может
изменить кинетическую энергию частицы.
• Часто лоренцевой силой называют сумму
электрических и магнитных сил:
Fл qE q[ v, B]
• здесь электрическая сила qE ускоряет частицу,
изменяет ее энергию.



















 physics
physics








