Магнитное поле. Вектор магнитной индукции

1.

Лекция 4
Содержание
• Магнитное поле. Вектор магнитной индукции
• Магнитное поле тока. Закон Био-Савара-Лапласа
• Теорема о циркуляции вектора индукции магнитного
поля
• Поток вектора магнитной индукции через замкнутую
поверхность
• Сила Ампера и сила Лоренца
• Работа по перемещению проводника с током в
магнитном поле
1

2.

Подобно тому, как в пространстве, окружающем
электрические заряды, возникает электростатическое поле, так и
в пространстве, окружающем токи и постоянные магниты,
возникает силовое поле, называемое магнитным.
Наличие магнитного поля обнаруживается по силовому
действию на внесенные в него проводники с током или
постоянные магниты.
В отличие от электрического поля, магнитного поле
действует только на движущиеся в этом поле электрические
заряды. Опыт показывает, что характер воздействия магнитного
поля на ток различен в зависимости от формы проводника, по
которому течет ток, от расположения проводника и от
направления тока. Следовательно, чтобы охарактеризовать
магнитное поле, надо рассмотреть его действие на определенный
ток.
2

3.

Подобно тому, как при исследовании электростатического поля
использовались точечные заряды, при исследовании магнитного
поля используется замкнутый плоский контур с током (рамка
с током), линейные размеры которого малы по сравнению с
расстоянием до токов, образующих магнитное поле.
Ориентация контура в пространстве определяется направлением
нормали к контуру. Направление нормали определяется
правилом правого винта: за положительное направление
нормали принимается направление поступательного движения
винта, рукоятка которого вращается в направлении тока,
текущего в рамке (рис.1).
3

4.

4

5.

Магнитное поле оказывает на рамку с током ориентирующее
действие, поворачивая ее определенным образом. За
направление магнитного поля в данной точке принимается
направление, вдоль которого располагается положительная
нормаль к рамке (на рис. – контур с током).
5

6.

Поведение рамки с током удобно описывать с помощью вектора
магнитного момента pm . Для плоского контура с током I
pm ISn ,
(6.1)
где S — площадь поверхности контура (рамки), n — единичный
вектор нормали к поверхности рамки. Направление pm
совпадает с направлением положительной нормали.
Вращающий момент сил, действующий на рамку с током,
зависит от свойств поля в данной точке и от свойств рамки:
M pm B ,
(6.2)
где B - вектор магнитной индукции, количественная
характеристика магнитного поля.
6

7.

Если в данную точку магнитного поля помещать рамки с
различными магнитными моментами, то на них действуют
различные вращающие моменты, однако отношение M max pm (
—
вращающий момент) для всех контуров одно и
Mмаксимальный
max
то же и поэтому может служить характеристикой магнитного
поля, называемой магнитной индукцией:
M max
B
.
pm
Магнитная индукция в данной точке однородного магнитного
поля определяется максимальным вращающим моментом,
действующим на рамку с магнитным моментом, равным
единице, когда нормаль к рамке перпендикулярна направлению
поля.
Единица магнитной индукции — тесла (Тл).
7

8.

Т.к. как магнитное поле является силовым, то его изображают с
помощью линий магнитной индукции — линий, касательные к
которым в каждой точке совпадают с направлением вектора B.
Их направление задается правилом
правого винта: рукоятка винта,
ввинчиваемого по направлению
тока, вращается в направлении
линий магнитной индукции.
Линии магнитной индукции всегда
замкнуты и охватывают
проводники с током.
8

9.

9

10.

Магнитное поле соленоида
10

11.

Закон Био - Савара – Лапласа
Рассмотрим проводник с током I .
11

12.

Магнитная индукция поля dB , создаваемого элементом dl
проводника с током I в некоторой точке А:
0 I dl r
dB
,
3
4 r
(6.3)
где dl — вектор, по модулю равный длине dl элемента
проводника и совпадающий по направлению с током,
r — радиус-вектор, проведанный из элемента проводника в
точку А поля, r — модуль радиуса-вектора r ,
0 4 10 7 Гн м — магнитная постоянная.
Направление dB перпендикулярно dl и r , т. е.
перпендикулярно плоскости, в которой они лежат, и совпадает с
касательной к линии магнитной индукции.
12

13.

Это направление может быть найдено по правилу нахождения
линий магнитной индукции (правилу правого винта):
направление вращения рукоятки винта дает направление dB ,
если поступательное движение винта соответствует
направлению тока в элементе.
Модуль вектора dB определяется выражением:
0 Idl sin
dB
,
2
4
r
где — угол между векторами dl и r .
Далее применяем принцип суперпозиции для магнитного
поля: магнитная индукция результирующего поля, создаваемого
несколькими токами или движущимися зарядами, равна
векторной сумме магнитных индукций полей, создаваемых
каждым током или движущимся зарядом в отдельности:
n
B Bi .
i 1
(6.4)
13

14.

Магнитное поле в центре кругового проводника с током.
Все элементы кругового
проводника с током создают в
центре магнитные поля
одинакового направления —
вдоль нормали от витка.
Поэтому сложение векторов dB
можно заменить сложением их
модулей.
14

15.

Так как все элементы проводника перпендикулярны радиусувектору ( sin 1) и расстояние всех элементов проводника до
центра кругового тока одинаково и равно R, то, согласно закону
Био - Савара - Лапласа
0 I
dB
dl .
2
4 R
Тогда
0 I
0 I
0 I
B dB
dl
2 R
.
2
2
4 R
2R
4 R
Следовательно, магнитная индукция поля в центре кругового
проводника с током
B
0 I
2R
.
(6.5)
15

16.

Циркуляция вектора B магнитного поля в вакууме
Аналогично циркуляции вектора напряженности
электростатического поля введем циркуляцию вектора
магнитной индукции.
Циркуляцией вектора B по заданному замкнутому контуру
называется интеграл
Bdl Bl dl ,
L
(6.6)
L
где dl — вектор элементарной длины контура, направленной
вдоль обхода контура,
Bl B cos — составляющая вектора B в направлении
касательной к контуру (с учетом выбранного
направления
обхода), — угол между векторами B и dl .
16

17.

Закон полного тока для магнитного поля в вакууме (теорема
о циркуляции вектора B ).
Циркуляция вектора B по произвольному замкнутому контуру
равна произведению магнитной постоянной 0 на
алгебраическую сумму токов, охватываемых этим контуром:
N
Bdl Bl dl 0 I k , где N — число проводников с токами,
L
L
k 1
охватываемых контуром произвольной
формы.
Каждый ток учитывается столько раз,
сколько раз он охватывается
контуром. Положительным считается
ток, направление которого образует с
направлением обхода по контуру
правовинтовую систему; ток
противоположного направления
считается отрицательным.
17

18.

Вывод:
Между выражениями для циркуляции векторов E и B
существует принципиальное различие.
Циркуляция вектора E электростатического поля всегда равна
нулю, т. е. электростатическое поле является потенциальным.
Циркуляция вектора B магнитного поля не равна нулю. Такое
поле называется вихревым.
Теорема о циркуляции вектора B имеет такое же значение, как
теорема Гаусса в электростатике,
т. к. позволяет находить магнитную индукцию поля без
применения закона Био-Савара- Лапласа.
18

19.

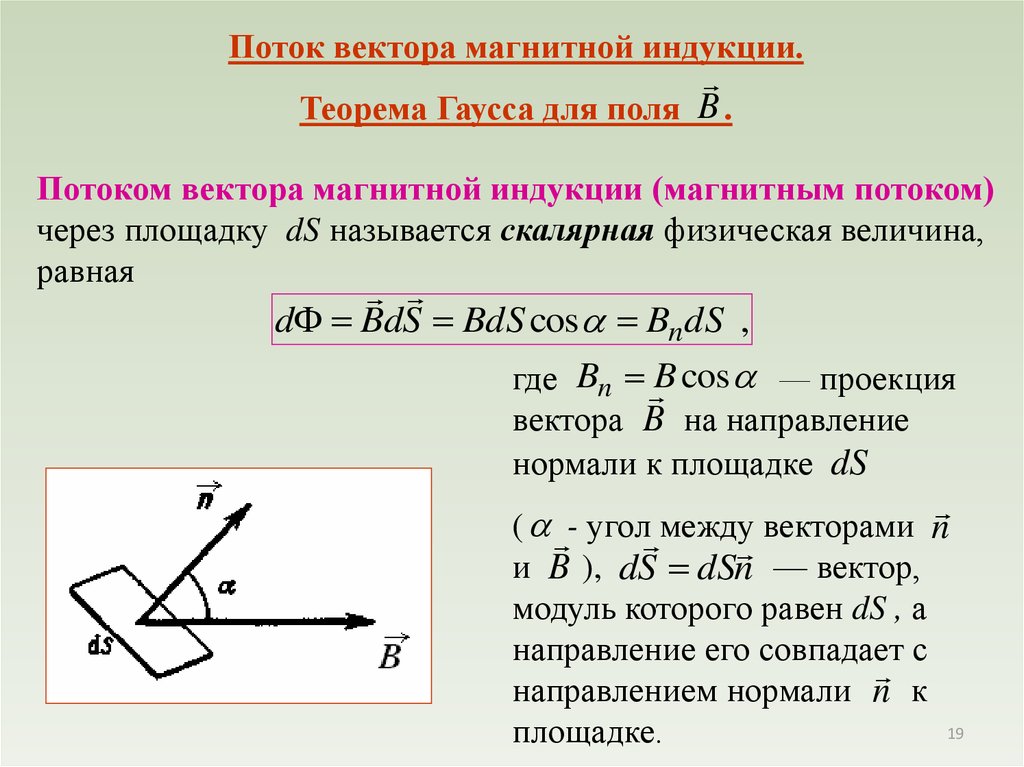
Поток вектора магнитной индукции.
Теорема Гаусса для поля B .
Потоком вектора магнитной индукции (магнитным потоком)
через площадку dS называется скалярная физическая величина,
равная
d BdS BdS cos Bn dS ,
где Bn B cos — проекция
вектора B на направление
нормали к площадке dS
( - угол между векторами n
и B ), dS dSn — вектор,
модуль которого равен dS , а
направление его совпадает с
направлением нормали n к
площадке.
19

20.

Поток вектора магнитной индукции через произвольную
поверхность S равен
BdS Bn dS .
S
(6.7)
S
Единица магнитного потока вебер (Вб): 1Вб — магнитный
поток, проходящий сквозь плоскую поверхность площадью 1м2,
расположенную перпендикулярно однородному магнитному
полю, индукция которого равна 1Тл. ( 1 Вб 1 Тл м 2).
Теорема Гаусса для поля B : поток вектора магнитной
индукции сквозь любую замкнутую поверхность равен нулю:
BdS 0 .
(6.8)
S
Эта теорема отражает факт отсутствия магнитных зарядов,
вследствие чего линии магнитной индукции не имеют ни начала, ни
20
конца и являются замкнутыми.

21.

Закон Ампера. Взаимодействие параллельных токов
Магнитное поле оказывает на рамку с током
ориентирующее
действие. Ампер установил, что сила dF , с которой магнитное
поле действует на элемент проводника dl с током, находящегося
в магнитном поле, равна
dF I dl B ,
(6.9)
где dl — вектор, по модулю
равный dl и совпадающий по
направлению с током, B — вектор магнитной индукции.
Направление вектора dF определяется по общим правилам
векторного произведения (или по правилу левой руки).
Модуль силы Ампера вычисляется по формуле
dF IBdl sin ,
где — угол между векторами dl и B .
(6.10)
21

22.

22

23.

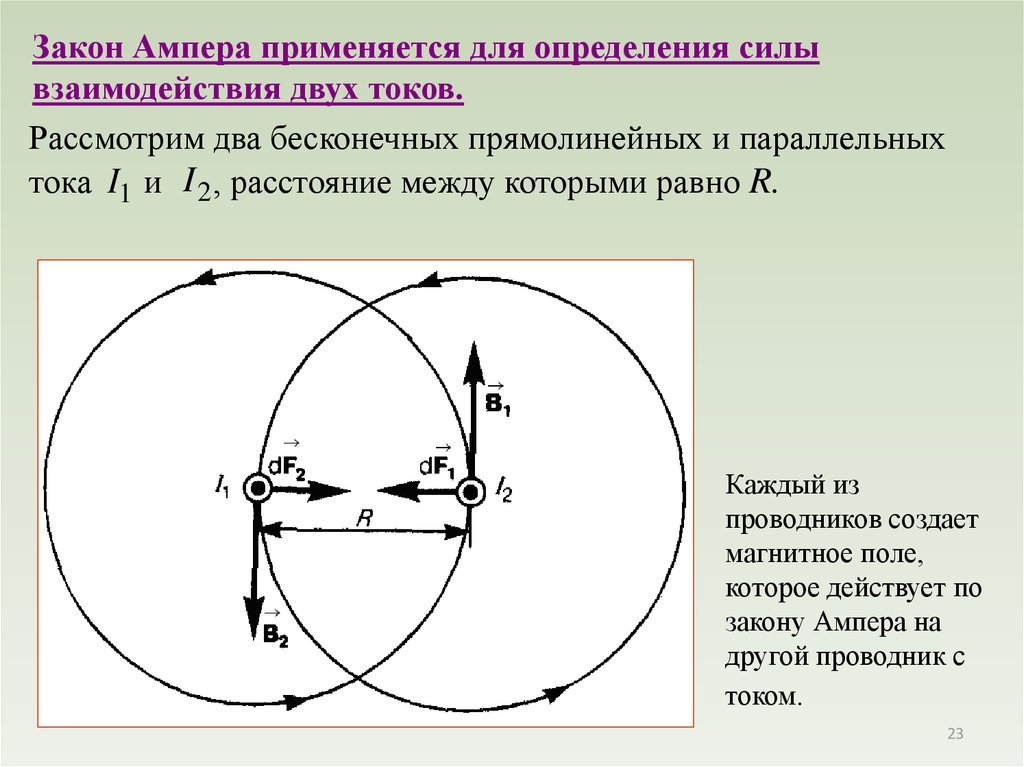
Закон Ампера применяется для определения силы
взаимодействия двух токов.
Рассмотрим два бесконечных прямолинейных и параллельных
тока I1 и I 2 , расстояние между которыми равно R.
Каждый из
проводников создает
магнитное поле,
которое действует по
закону Ампера на
другой проводник с
током.
23

24.

Рассмотрим, с какой силой действует магнитное поле тока
I1
I1
на элемент
dl второго проводника с током . Ток создает
I2
вокруг себя магнитное поле, линии магнитной индукции
которого представляют собой концентрические окружности.
Направление вектора B1 определяется правилом правого винта,
а его модуль равен:
0 I1
B1
.
2 R
Направление силы dF1 , с которой поле B1 действует на
участок dl второго тока, определяется по правилу левой руки и
указано на рисунке. Модуль силы, с учетом
того, что угол между
B1 равен:
I2
элементами тока
и вектором
прямой,
dF1 I 2 B1dl ;
подставляя значение для B1, получим
0 I1I 2
dF1
dl .
2 R
24

25.

Cила dF2 с которой магнитное поле тока I 2 действует на
элемент dl первого проводника с током I1, направлена в
противоположную сторону и по модулю равна:
0 I1I 2
dF2 I1B2 dl
dl .
2 R
Сравнение выражений для сил dF1 и dF2 показывает:
dF1 dF2 ,
т. е. два параллельных тока одинакового направления
притягиваются друг к другу с силой
0 I1I 2
dF
dl .
2 R
(6.11)
Если токи имеют противоположные направления, то,
используя правило левой руки, можно показать, что между ними
действует сила отталкивания, определяемая формулой (6.11).
25

26.

Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на
проводники с током, но и на отдельные заряды, движущиеся в
магнитном поле.
Сила, действующая на электрический заряд q , движущийся в
магнитном поле со скоростью , называется силой Лоренца и
выражается формулой
(6.12)
F q B ,
где B - индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила
левой руки: если ладонь
левой руки расположить так, чтобы в
нее входил вектор B , а четыре вытянутых пальца направить
вдоль вектора (для q 0 направления I и совпадают,
для q 0 — противоположны), то отогнутый большой палец
покажет направление силы, действующей на положительный
26
заряд.

27.

На рис. показана взаимная ориентация векторов и B (поле
направлено к нам, на рисунке показано точками) и F для
положительного заряда. На отрицательный заряд сила действует
в противоположном направлении.
Модуль силы Лоренца равен:
F q B sin ,
где — угол между и B .
Магнитное поле не действует на покоящийся электрический заряд.
В этом существенное отличие магнитного поля от электрического.
Магнитное поле действует только на движущиеся в нем заряды.
27

28.

Сила Лоренца всегда перпендикулярна скорости
движения заряженной частицы, поэтому она
изменяет только направление этой скорости, не
изменяя ее модуля.
Следовательно, сила Лоренца работы не совершает
и кинетическая энергия этой частицы при
движении в магнитном поле не изменяется.
Если на движущийся электрический
заряд кроме
магнитного поля с индукцией
поле
B действует и электрическое
с напряженностью E , то результирующая сила F ,
приложенная к заряду, равна векторной сумме сил — силы,
действующей со стороны электрического поля, и силы Лоренца:
F qE q B
Это выражение называется формулой Лоренца.
(6.13)
28

29.

Магнитны ловушки - специальные конфигурации магнитного поля, способные
длительное время удерживать заряженные частицы внутри определённого
объёма пространства. {Траектория заряженной частицы как бы навивается на
29
линии магнитной индукции. }

30.

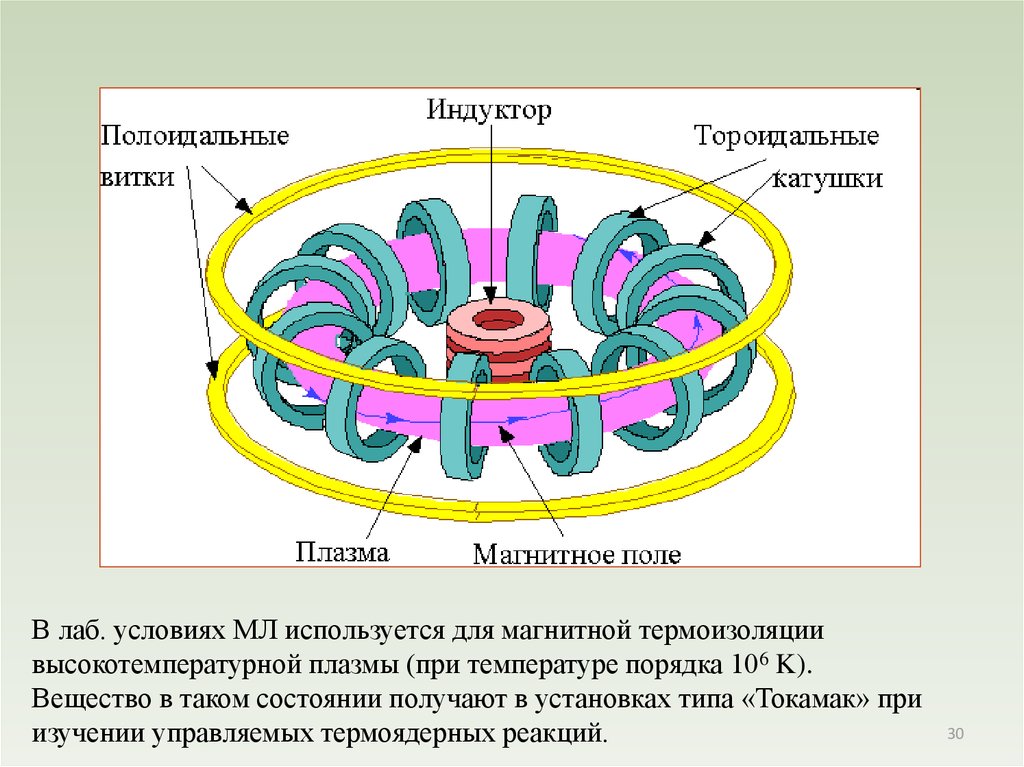
В лаб. условиях МЛ используется для магнитной термоизоляции
высокотемпературной плазмы (при температуре порядка 106 K).
Вещество в таком состоянии получают в установках типа «Токамак» при
изучении управляемых термоядерных реакций.
30

31.

М Л природного происхождения является магнитное поле Земли.
31

32.

Работа по перемещению проводника и контура с током в
магнитном поле
Рассмотрим проводник длиной l с током I (он может свободно
перемещаться), помещенный в однородное внешнее магнитное
поле, перпендикулярное плоскости контура. Сила, определяемая
по закону Ампера, равна: F IBl .
32

33.

Пусть под действием этой силы проводник переместится
параллельно самому себе на расстояние dx из положения 1 в
положение 2. Работа, совершаемая магнитным полем, равна
dA Fdx IBldx IBdS Id ,
так как ldx dS — площадь, пересекаемая проводником при его
перемещении в магнитном поле, BdS d — поток вектора
магнитной индукции, пронизывающий эту площадь.
Т.О.,
dA Id ,
т. е. работа по перемещению проводника с током в магнитном
поле равна произведению силы тока на магнитный поток,
пересекаемый движущимся проводником.
Полученная формула справедлива
и для произвольного
направления вектора B .
33

34.

Если разбить контур произвольной формы, по которому
течет ток, на маленькие участки, то к каждому участку можно
применить полученную формулу. Поэтому работа по
перемещению всего контура с током в магнитном поле равна:
2
A Id I 2 1 I ,
(6.14)
1
т. е. работа по перемещению замкнутого контура с током в
магнитном поле равна произведению силы тока в контуре на
изменение магнитного потока сквозь контур.
Полученная формула остается справедливой для контура любой
формы в произвольном магнитном поле.
34