Магнитное поле. Лекция 11

1.

Лекция 11.
Магниное поле
Составитель:
доцент кафедры МФиИТ,
канд. физ.-мат. наук Маринова С.А.
Кемерово 2019
1

2.

План лекции
1. Магнитное поле и его характеристики
2. Закон Био – Савара – Лапласа
3. Закон Ампера. Взаимодействие параллельных токов
4. Действие магнитного поля на движущийся заряд
5. Поток вектора магнитной индукции. Теорема Гаусса для магнитной
индукции
2

3.

1. Магнитное поле и его характеристики
Магнитное поле – силовое поле, действующее на движущиеся электрические
заряды и на тела, обладающие магнитным моментом, независимо от состояния их
движения. Наличие магнитного поля обнаруживается по силовому действию на
внесенные в него проводники с током или постоянные магниты.
Магнитное действует только на движущиеся в нем электрические заряды.
Характер воздействия магнитного поля на ток различен в зависимости от формы
проводника, по которому течет ток, от расположения проводника и от направления
тока.
При исследовании магнитного поля пользуются замкнутым плоским контуром с
током (рамка с током), линейные размеры которого малы по сравнению с
расстоянием до токов, образующих магнитное поле.
3

4.

Ориентация контура в пространстве определяется направлением нормали к
контуру, задаваемого правилом правого винта:
за
положительное
направление
нормали
принимается
направление
поступательного движения винта, головка которого вращается в направлении
тока, текущего в рамке.
За направление магнитного поля в данной точке принимается направление,
вдоль которого располагается положительная нормаль к рамке.
4

5.

На рамку с током в магнитном поле действует пара сил,
вращающий момент которых зависит как от свойств поля в данной
точке, так и от свойств рамки и определяется по формуле
M pm , B ,
где pm– вектор магнитного момента рамки с током;
B – вектор магнитной индукции.
Для плоского контура с током I и площадью поверхности S
pm ISn.
5

6.

Магнитная индукция – векторная величина, являющаяся силовой
характеристикой магнитного поля (его действия на заряженные частицы) в данной
точке пространства; определяется максимальным вращающим моментом,
действующим на рамку с магнитным моментом, равным единице, когда нормаль к
рамке перпендикулярна направлению поля
M
B max .
pm
Магнитное поле является силовым и его изображают с помощью линий
магнитной индукции – линий, касательные к которым в каждой точке совпадают с
направлением вектора B . Их направление задается правилом правого винта.
Линии магнитной индукции всегда замкнуты и охватывают проводники с током.
6

7.

Еще одной характеристикой магнитного поля является вектор напряженности H
магнитного поля. Для однородной изотропной среды вектор магнитной индукции
связан с вектором напряженности следующим соотношением:
B 0 H ,
7 Гн
где 0 4 10
– магнитная постоянная;
м
– магнитная проницаемость среды,
показывающая, во сколько раз магнитное поле
макротоков усиливается за счет поля
микротоков среды
7

8.

2. Закон Био – Савара – Лапласа
Закон Био – Савара – Лапласа (также Закон Био – Савара) – физический закон для
определения вектора индукции магнитного поля, порождаемого постоянным
электрическим током. Был установлен экспериментально в 1820 году Био и Саваром
и сформулирован в общем виде Лапласом.
Закон Био – Савара – Лапласа для проводника с током I ,
элемент dl которого создает в некоторой точке A индукцию
поля dB , записывается в виде
0 I dl , r
dB
.
3
4
r
8

9.

Модуль вектора dB определяется выражением
0 Idl sin
dB
,
2
4
r
где – угол между векторами dl и r .
Для магнитного поля, как и для электрического, справедлив принцип
суперпозиции: вектор магнитной индукции результирующего поля, создаваемого
несколькими токами или движущимися зарядами, равен векторной сумме магнитных
индукций складываемых полей, создаваемых каждым током или движущимся
зарядом в отдельности:
n
B Bi .
i 1
9

10.

Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу
бесконечной длины.
2I
B 0
4 R
10

11.

Магнитное поле в центре кругового проводника с током. Все элементы
кругового проводника с током создают в центре магнитные поля одинакового
направления – вдоль нормали от витка.
I
B 0
2R
11

12.

3. Закон Ампера.
Взаимодействие параллельных токов
Закон Ампера
сила dFА , с которой магнитное поле действует на элемент проводника dl с током,
находящегося в магнитном поле, равна
dFА I dl , B ,
где dl – вектор, по модулю равный dl и совпадающий по направлению с током.
Направление вектора dFА может быть найдено, согласно, по общим правилам
векторного произведения, откуда следует правило левой руки: если ладонь левой
руки расположить так, чтобы в нее входил вектор B , а четыре вытянутых пальца – по
направлению тока в проводнике, то отогнутый большой палец покажет направление
силы, действующей на ток.
12

13.

Модуль силы Ампера вычисляется по формуле двух токов.
dFА IBdl sin .
Закон Ампера применяется для определения силы взаимодействия двух токов.
Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I 2 , расстояние
между которыми равно R . Каждый из проводников создает магнитное поле, которое
действует по закону Ампера на другой проводник с током.
Два параллельных тока одинакового направления притягиваются друг к другу с
силой
0 2 I1 I 2
dF
dl.
4 R
13

14.

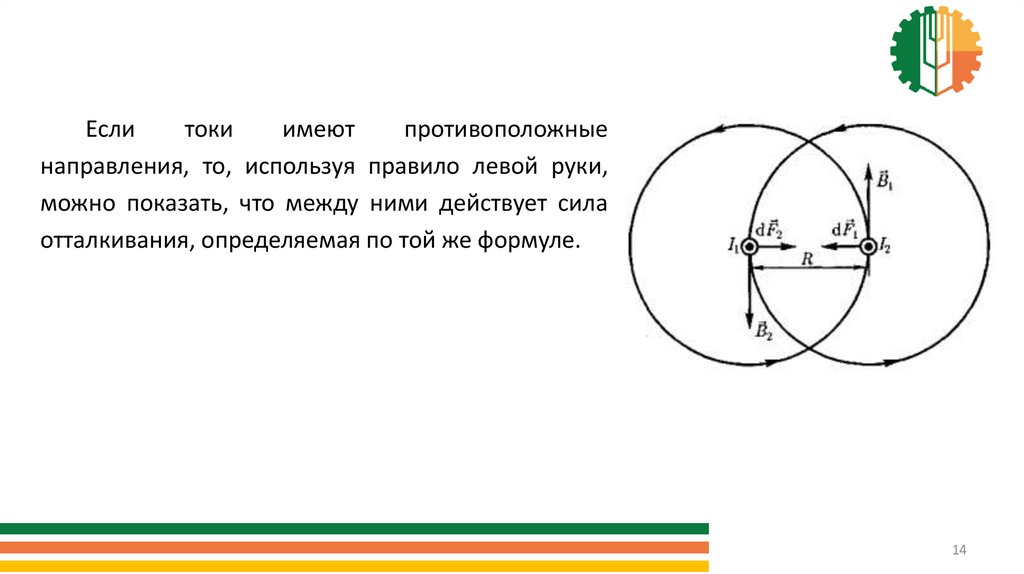
Если
токи
имеют
противоположные
направления, то, используя правило левой руки,
можно показать, что между ними действует сила
отталкивания, определяемая по той же формуле.
14

15.

4. Действие магнитного поля на движущийся заряд
Магнитное поле действует не только на проводники с током, но и на отдельные
заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд
q, движущийся в магнитном поле со скоростью , называется силой Лоренца и
выражается формулой
F q , B .
Направление силы Лоренца определяется с помощью правила левой руки: если
ладонь левой руки расположить так, чтобы в нее входил вектор B , а четыре
вытянутых пальца направить вдоль вектора (для q 0 направления I и совпадают,
для q 0 – противоположны), то отогнутый большой палец покажет направление
силы, действующей на заряд.
15

16.

Модуль силы Лоренца
F q B sin .
Если на движущийся электрический заряд помимо магнитного поля с индукцией
Bдействует и электрическое поле с напряженностью E, то результирующая сила F,
приложенная к заряду, равна векторной сумме сил – силы, действующей со стороны
электрического поля, и силы Лоренца:
F qE q , B .
Это выражение называется формулой Лоренца.
16

17.

5. Поток вектора магнитной индукции.
Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через площадку – скалярная физическая
величина, равная
d B BdS Bn dS ,
где Bn B cos – проекция вектора B на направление нормали к площадке dS ;
– угол между векторами B и n ;
dS ndS – вектор, модуль которого равен dS , а направление его совпадает с
направлением нормали n к площадке.
Поток вектора магнитной индукции B через произвольную поверхность S равен
B BdS Bn dS .
S
S
17

18.

Теорема Гаусса для вектора магнитной индукции
поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:
BdS B dS 0.
n
S
S
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии
магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
18