Similar presentations:
Медианы, биссектрисы и высоты треугольника
1.
Медианы, биссектрисы ивысоты треугольника
2.
медианы треугольникабиссектрисы треугольника
высоты треугольника
3.
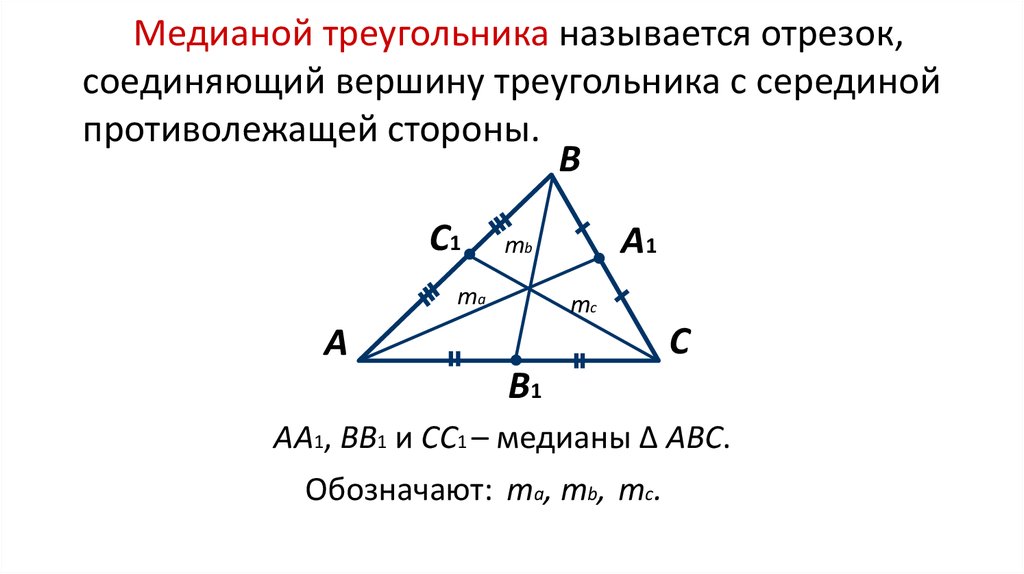
Медианой треугольника называется отрезок,соединяющий вершину треугольника с серединой
противолежащей стороны.
В
C1
A1
mb
ma
mc
С
А
B1
АA1, ВB1 и СC1 – медианы ∆ АВС.
Обозначают: ma, mb, mc.
4.
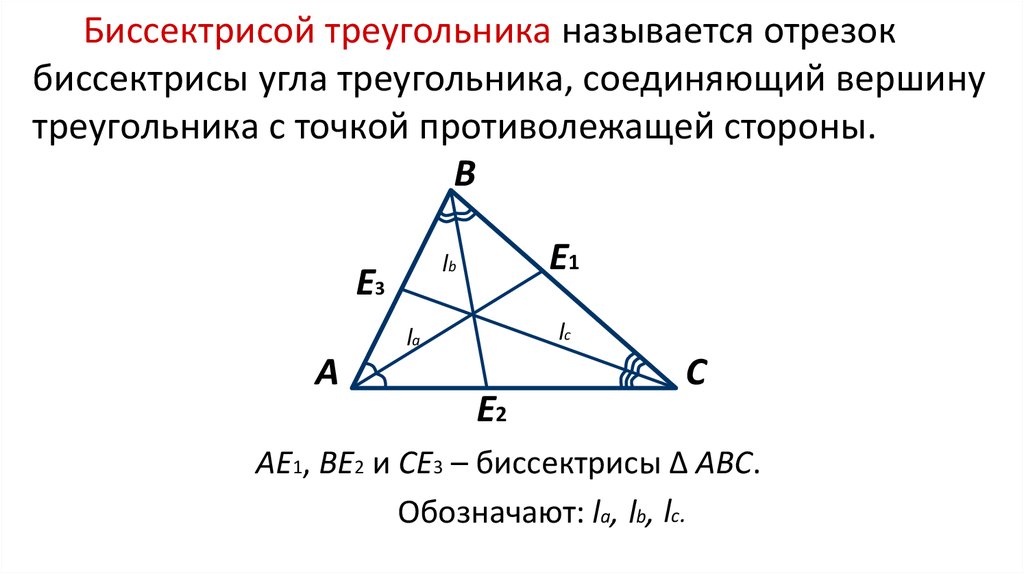
Биссектрисой треугольника называется отрезокбиссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противолежащей стороны.
B
E1
lb
E3
lc
la
А
E2
C
АE1, ВE2 и СE3 – биссектрисы ∆ АВС.
Обозначают: la, lb, lc.
5.
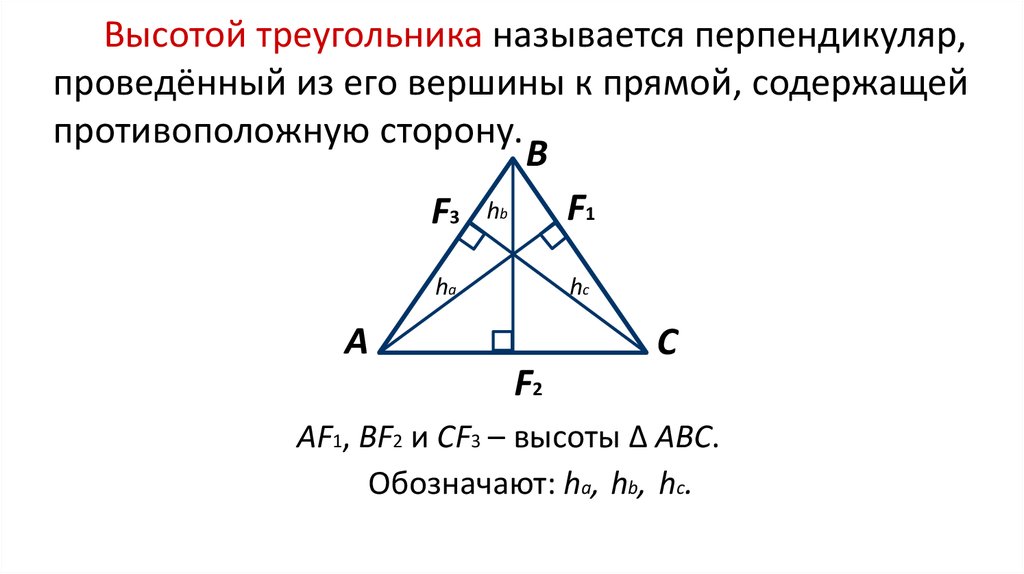
Высотой треугольника называется перпендикуляр,проведённый из его вершины к прямой, содержащей
противоположную сторону.
В
F1
F3 h
b
ha
hc
А
С
F2
АF1, ВF2 и СF3 – высоты ∆ АВС.
Обозначают: ha, hb, hc.
6.
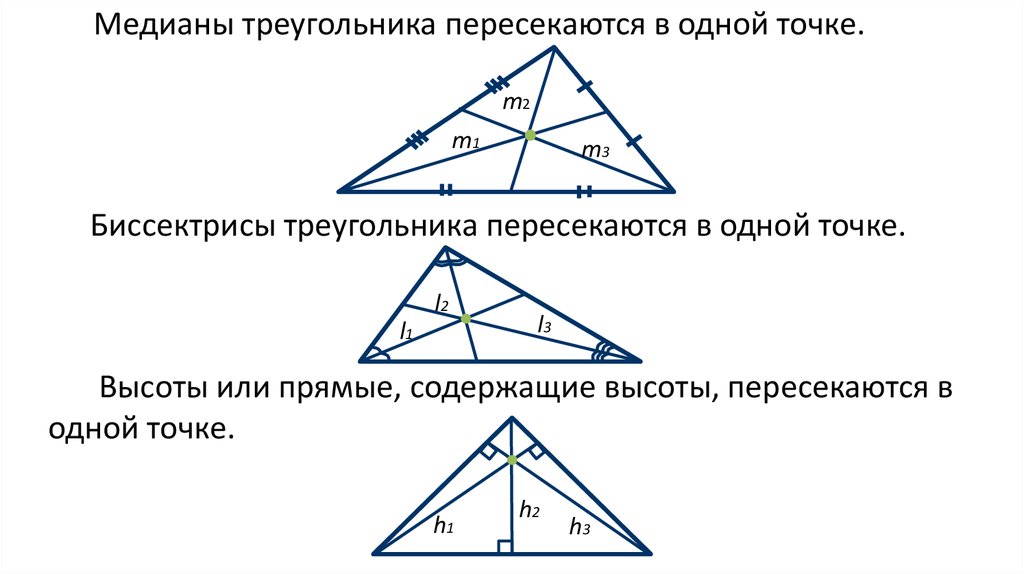
Медианы треугольника пересекаются в одной точке.m2
m1
m3
Биссектрисы треугольника пересекаются в одной точке.
l2
l1
l3
Высоты или прямые, содержащие высоты, пересекаются в
одной точке.
h1
h2
h3
7.
Может ли точка пересечения высот лежатьвне треугольника?
h2
h1
h3
8.
Может ли точка пересечения высот лежатьв вершине треугольника?
h1
h2
h3
9.
Задача. Отрезок BD – медиана треугольника АВС,отрезок ВЕ – медиана треугольника DBC. Чему равна
длина отрезка АС, если отрезок ЕС равен 4 сантиметра?
Решение.
В
Так как ВЕ – медиана ∆ DВС, то DE = EC,
следовательно, DС = 2EC, DС = 2 4 = 8 см.
ВD – медиана ∆ AВС, значит AD = DC,
А
следовательно, AС = 2DC, AС = 2 8 = 16 см.
Ответ: 16 см.
D
E
С
10.
Задача. Отрезок AD – медиана треугольника АВС.Точка Е лежит на луче АD так, что AD = DЕ. Докажите,
что треугольник АDВ равен треугольнику CDE.
Доказательство.
А
Так как AD – медиана ∆ AВС, то СD = DB,
Рассмотрим ∆ ADB и ∆ СDЕ.
С
АD = DЕ,
СD = DВ, так как AD – медиана,
∠ ADB = ∠CDE ( как вертикальные).
Следовательно, ∆ ADB = ∆ СDЕ
(по первому признаку).
D
E
В






 mathematics
mathematics








