Медианы, биссектрисы и высоты треугольника

1.

Медианы, биссектрисы и высоты
треугольника

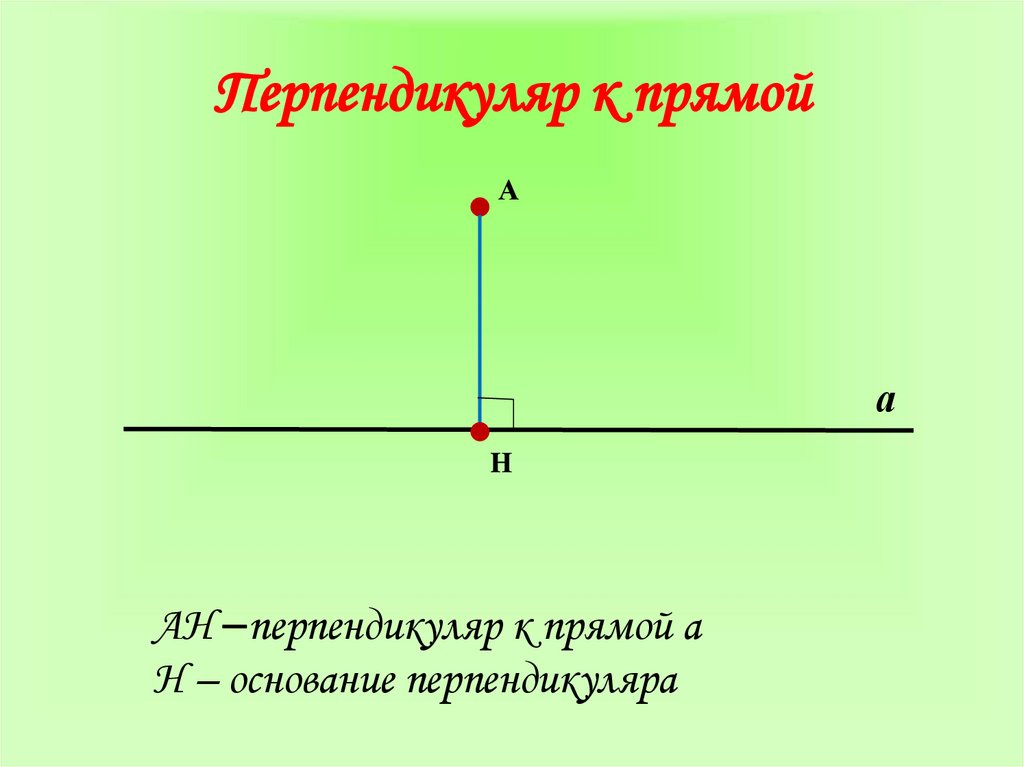
2. Перпендикуляр к прямой

А
а
H
АH перпендикуляр к прямой а
H – основание перпендикуляра

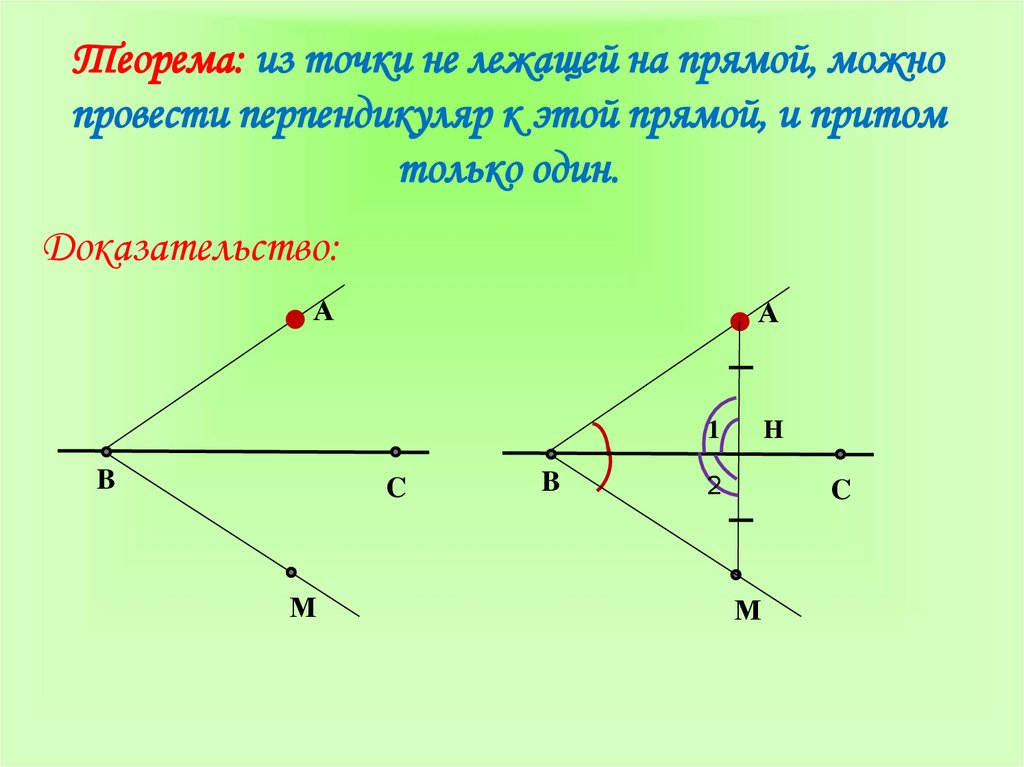
3. Теорема: из точки не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Доказательство:
А
А
1
B
C
М
B
H
2
C
М

4.

А
B
H 1`
H
C
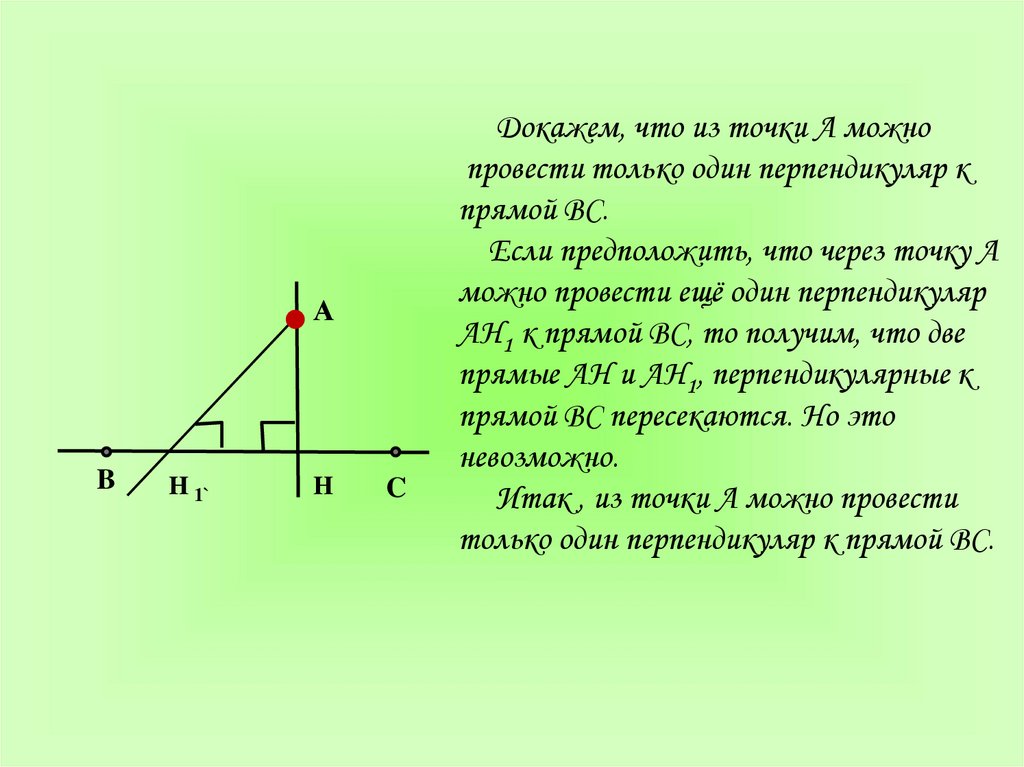
Докажем, что из точки А можно
провести только один перпендикуляр к
прямой ВС.
Если предположить, что через точку А
можно провести ещё один перпендикуляр
АН1 к прямой ВС, то получим, что две
прямые АН и АН1, перпендикулярные к
прямой ВС пересекаются. Но это
невозможно.
Итак , из точки А можно провести
только один перпендикуляр к прямой ВС.

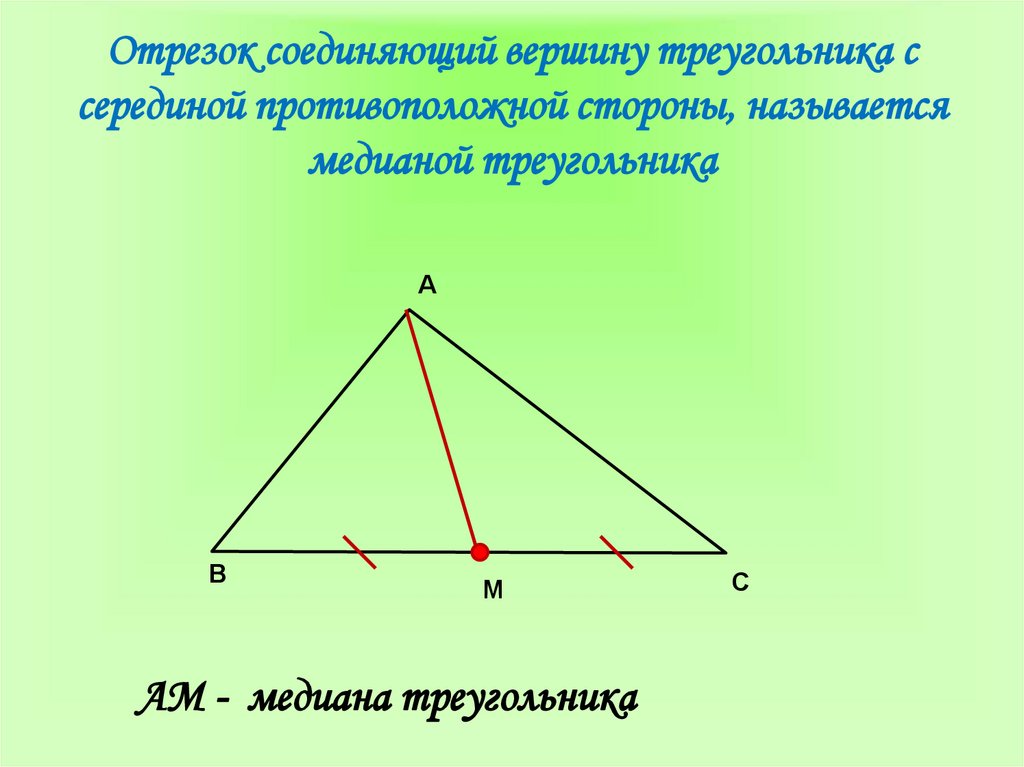
5. Отрезок соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника

А
В
М
АМ - медиана треугольника
С

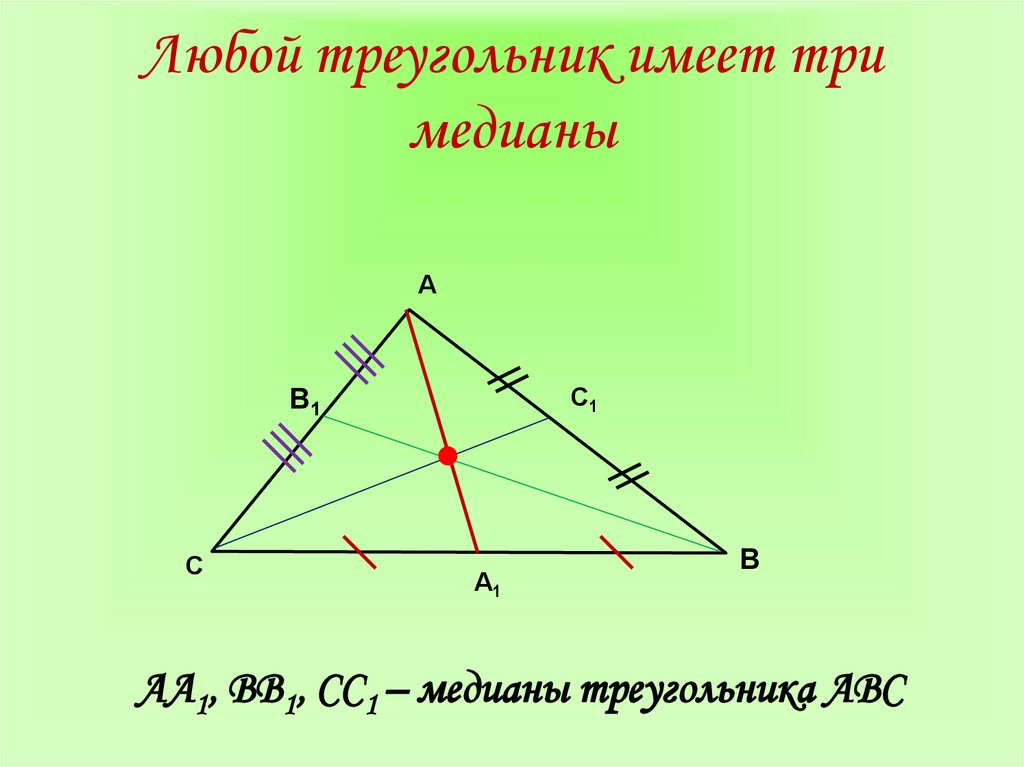
6. Любой треугольник имеет три медианы

А
С1
В1
С
А1
В
АА1, ВВ1, СС1 – медианы треугольника АВС

7.

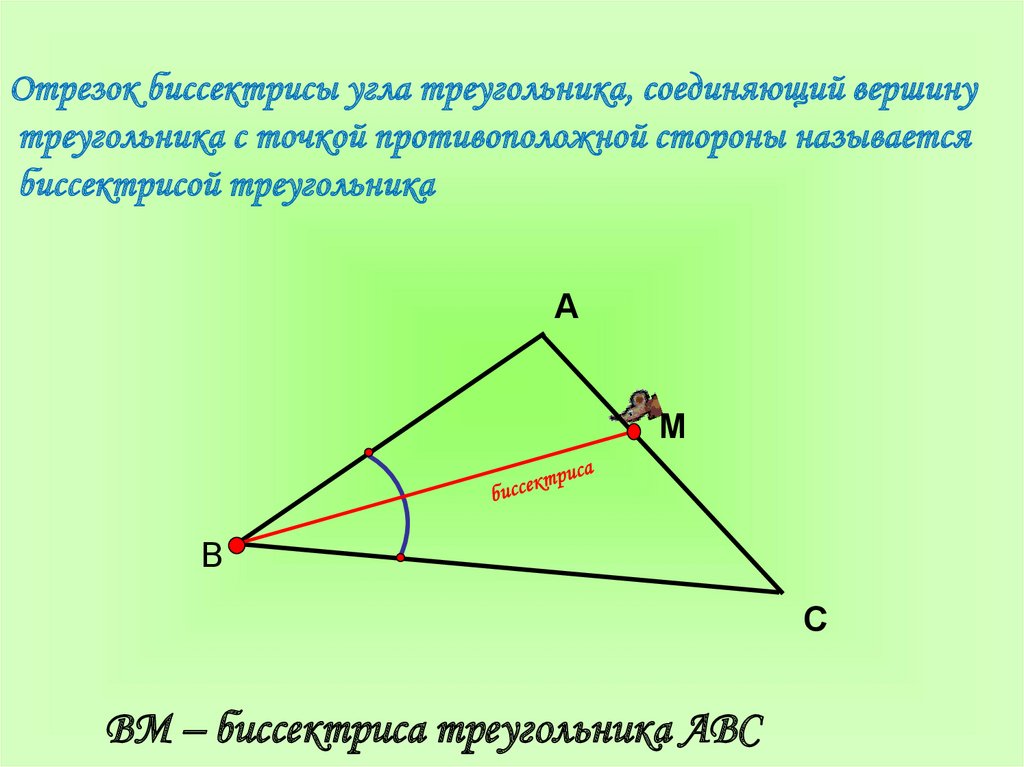
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны называется
биссектрисой треугольника
А
M
В
С
BM – биссектриса треугольника АВС

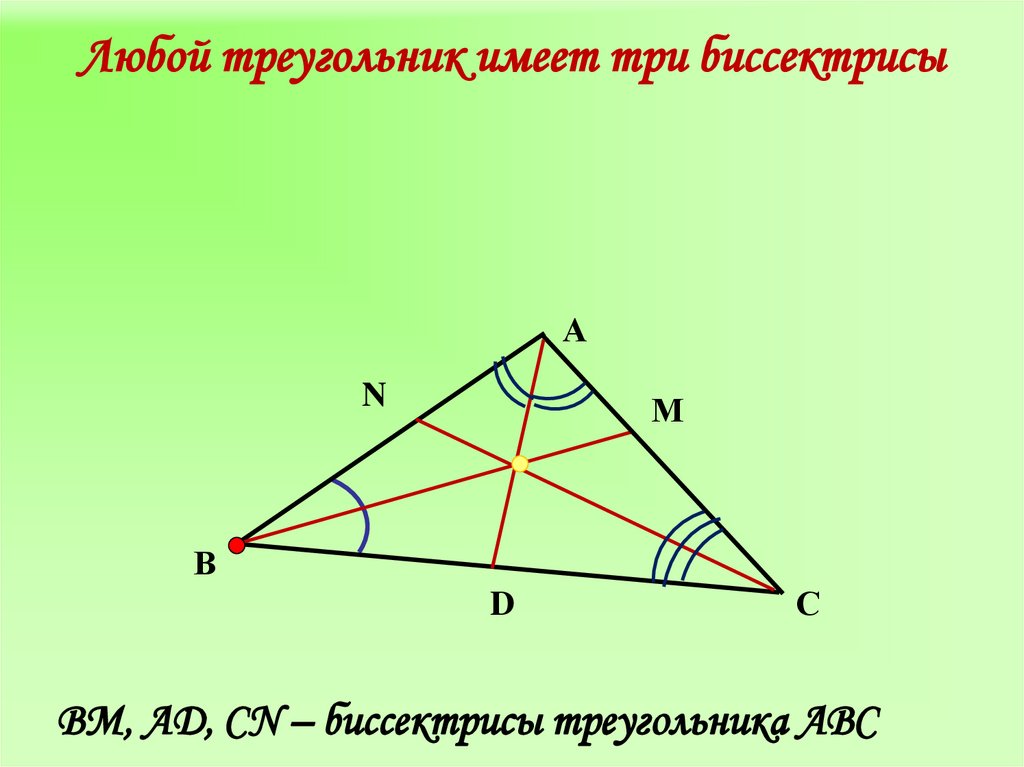
8. Любой треугольник имеет три биссектрисы

А
N
М
В
D
С
BM, АD, CN – биссектрисы треугольника АВС

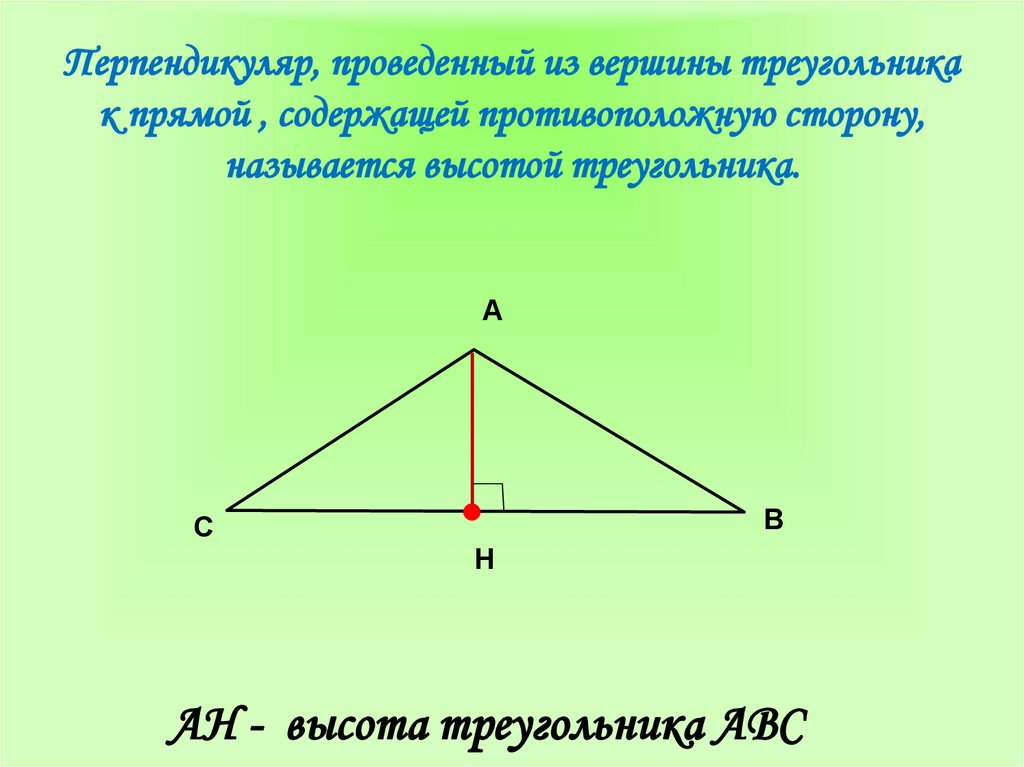
9. Перпендикуляр, проведенный из вершины треугольника к прямой , содержащей противоположную сторону, называется высотой

треугольника.
А
В
С
H
АH - высота треугольника АВС

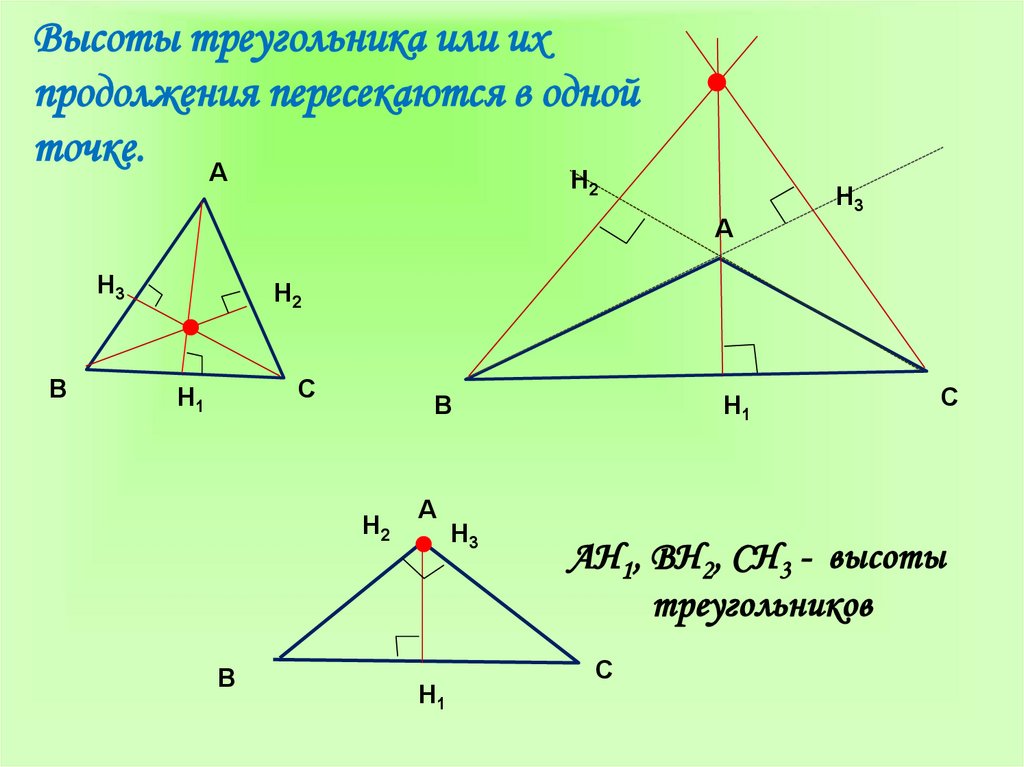
10. Высоты треугольника или их продолжения пересекаются в одной точке.

А
H2
А
H3
В
H3
H2
С
H1
В
H2
В
H1
С
А
H3
AH1, ВH2, СH3 - высоты
треугольников
С
H1

11.

Литература
1. Геометрия 7 – 9 классы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и
др., М. Просвещение, 2009 г.
2. Анимация http://animashky.ru/index/0-11?25-6