Similar presentations:
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника
1. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника.
Цель урока: познакомиться с новымигеометрическими понятиями. Доказать
теорему о перпендикуляре.
1
2.
Аа
Н
АН а
А а; Н
а
Определение: отрезок АН называется
перпендикуляром, проведённым из точки А к прямой
а, если прямые АН и а перпендикулярны. Точка Н
называется основанием перпендикуляра.
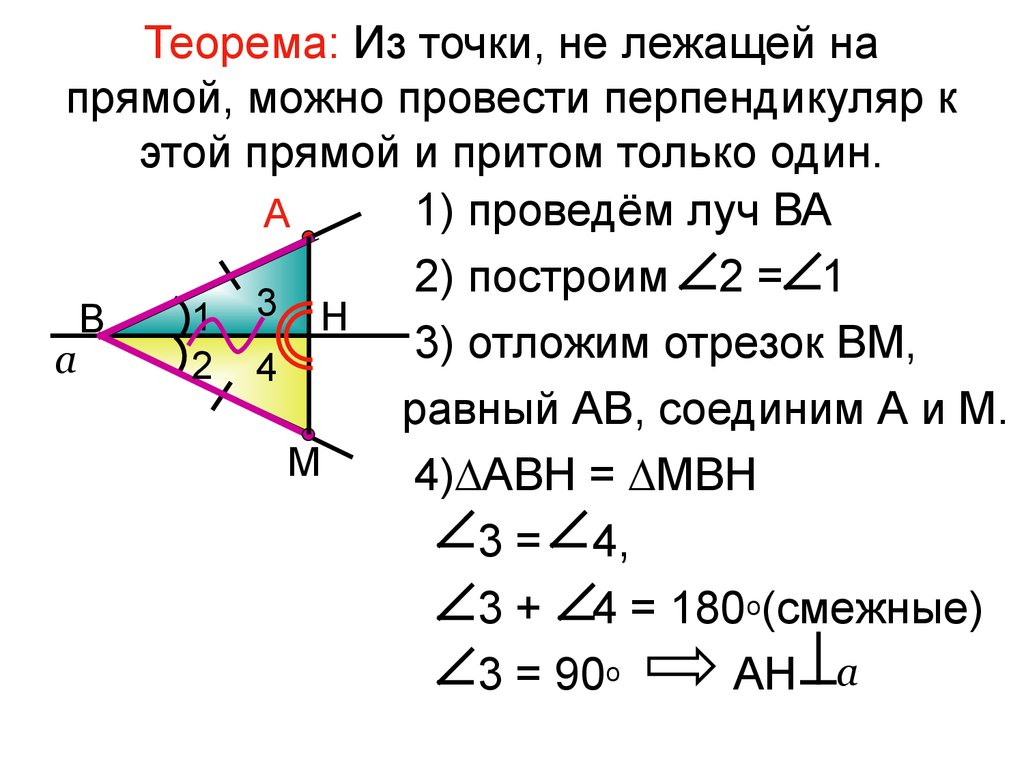
3. Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом только один.
1) проведём луч ВАА
2) построим 2 = 1
1 3 Н
В
3)
отложим
отрезок
ВМ,
а
2 4
равный АВ, соединим А и М.
М
4)∆АВН = ∆МВН
3 = 4,
3 + 4 = 180о(смежные)
3 = 90о
АН а
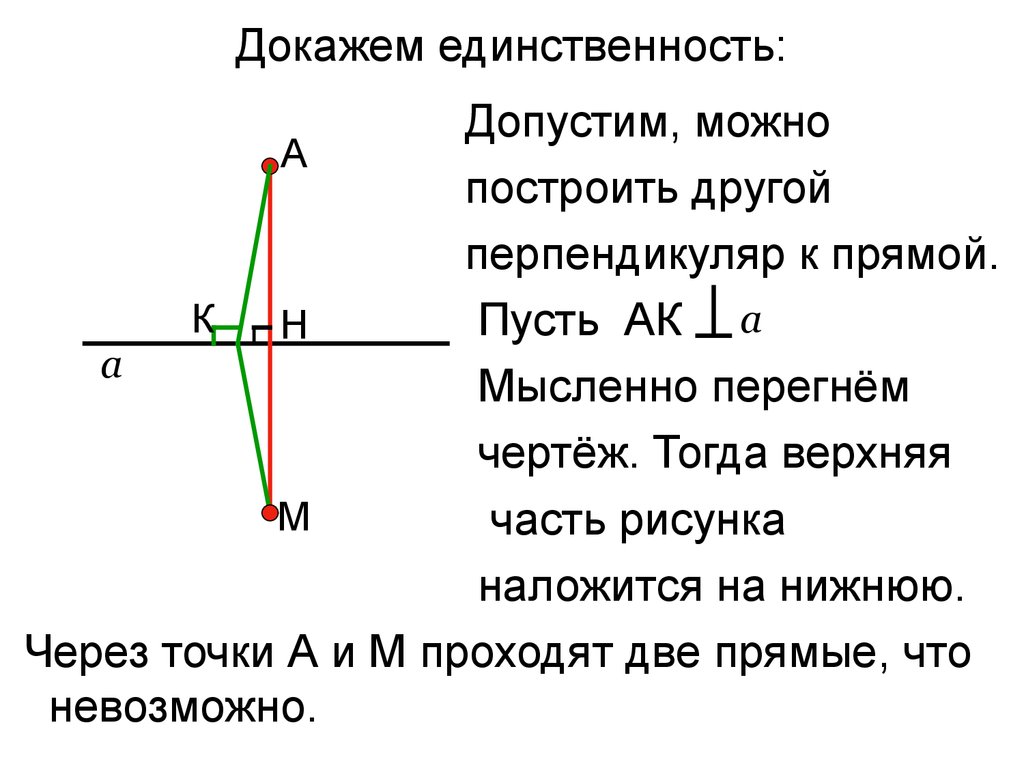
4. Докажем единственность:
Допустим, можноА
построить другой
перпендикуляр к прямой.
К
Пусть АК а
Н
а
Мысленно перегнём
чертёж. Тогда верхняя
М
часть рисунка
наложится на нижнюю.
Через точки А и М проходят две прямые, что
невозможно.
5. № 105.(устно)
1)Доказать: ∆АВD = ∆CDB2) Найти АВС
А
С
?
а
В
44о
D
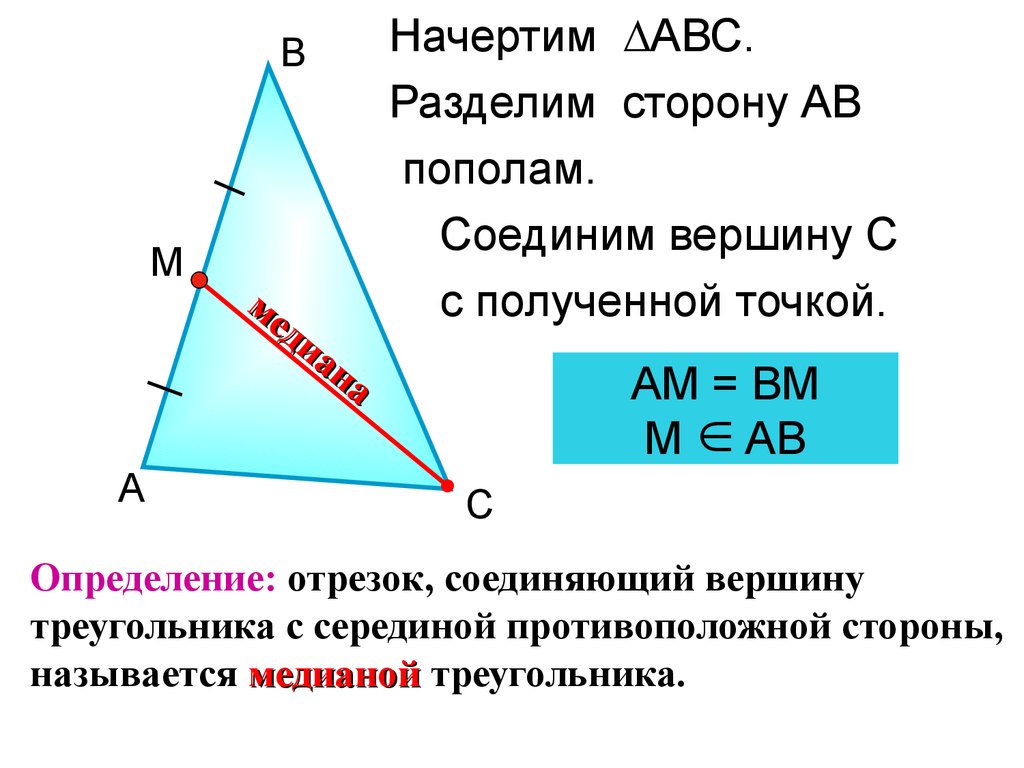
6.
ВМ
А
ме
ди
ан
а
Начертим ∆АВС.
Разделим сторону АВ
пополам.
Соединим вершину С
с полученной точкой.
АМ = ВМ
М АВ
С
Определение: отрезок, соединяющий вершину
треугольника с серединой противоположной стороны,
называется медианой треугольника.
7.
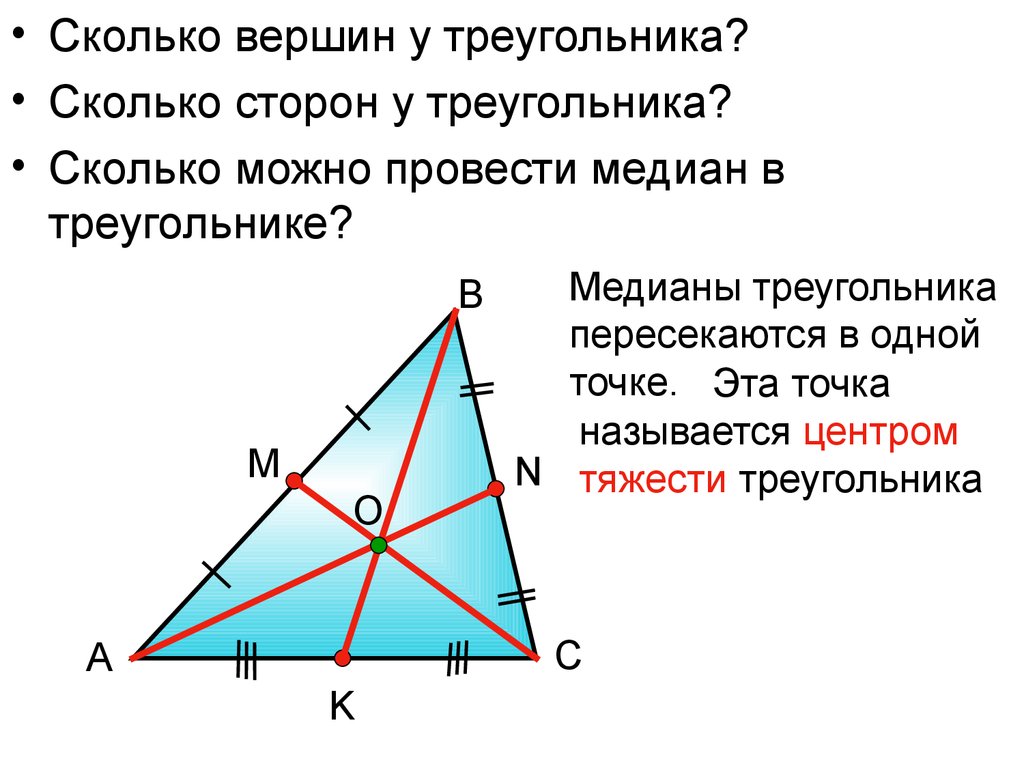
• Сколько вершин у треугольника?• Сколько сторон у треугольника?
• Сколько можно провести медиан в
треугольнике?
В
М
О
Медианы треугольника
пересекаются в одной
точке. Эта точка
называется центром
N тяжести треугольника
С
А
K
8.
ВK
би
сс е
кт
ри
са
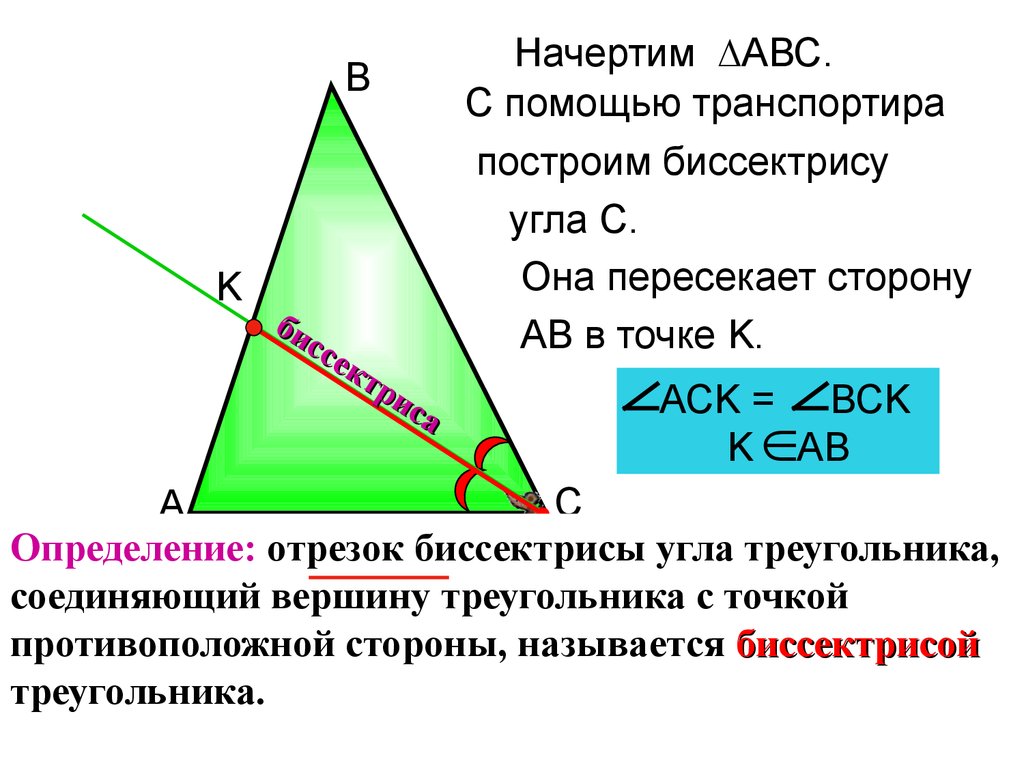
Начертим ∆АВС.
С помощью транспортира
построим биссектрису
угла С.
Она пересекает сторону
АВ в точке K.
АСK = ВСK
K АВ
С
А
Определение: отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой
противоположной стороны, называется биссектрисой
треугольника.
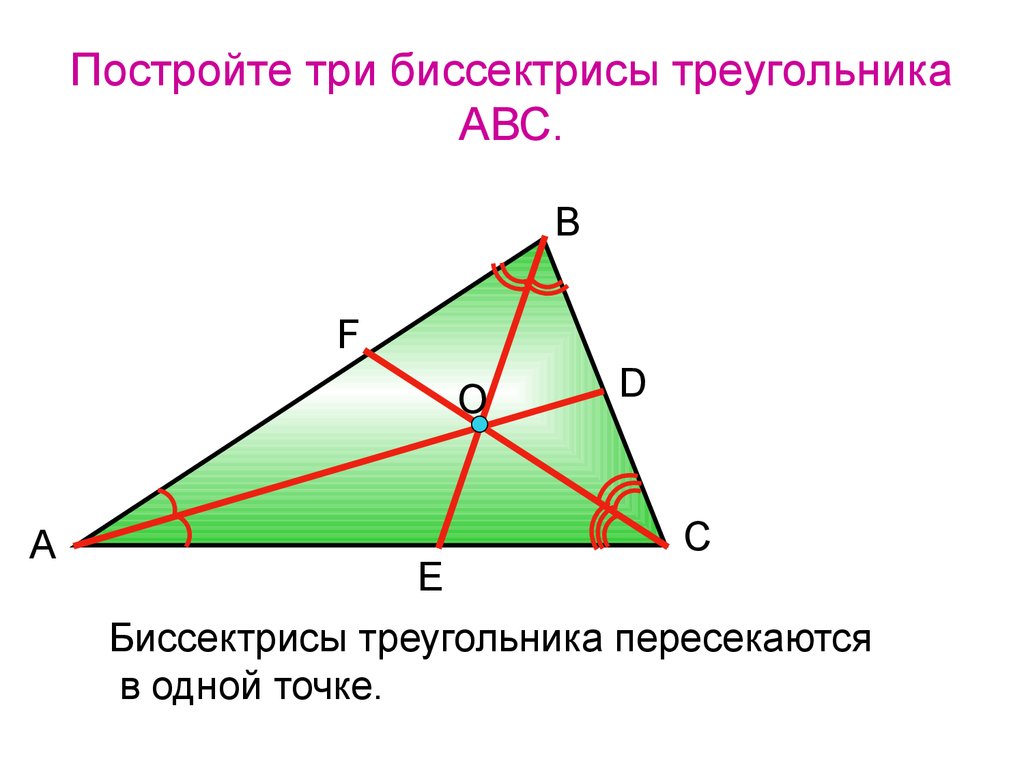
9. Постройте три биссектрисы треугольника АВС.
ВF
O
А
E
D
С
Биссектрисы треугольника пересекаются
в одной точке.
10.
ВВ
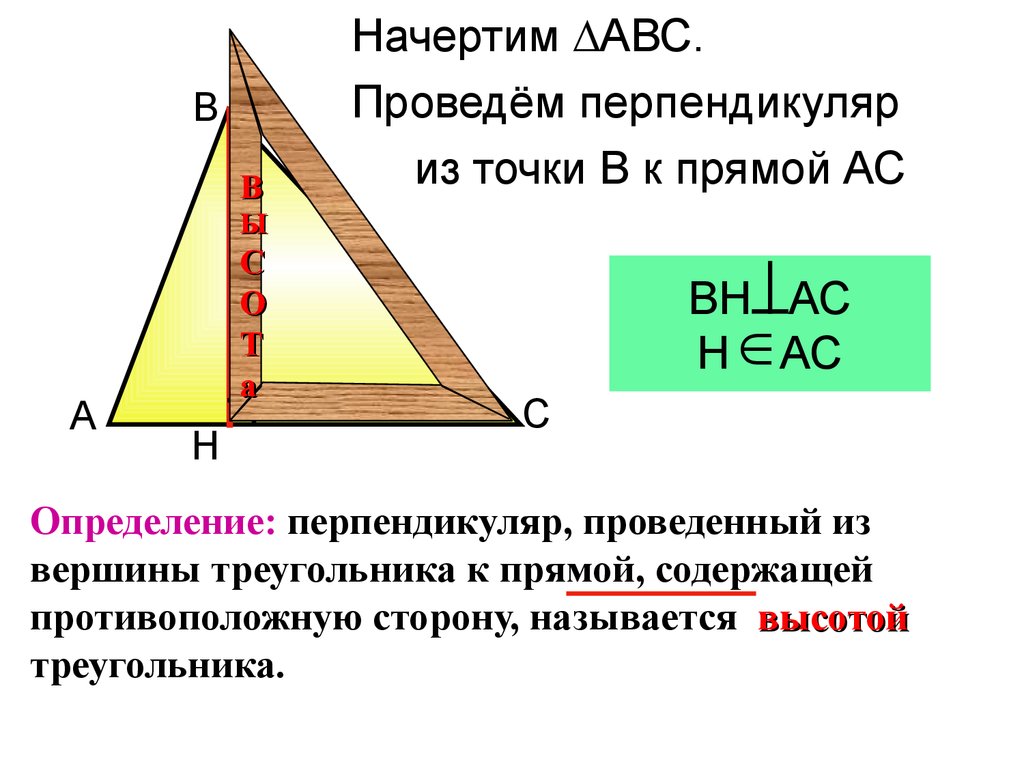
Начертим ∆АВС.
Проведём перпендикуляр
из точки В к прямой АС
Ы
А
С
О
Т
а
Н
ВН АС
Н АС
С
Определение: перпендикуляр, проведенный из
вершины треугольника к прямой, содержащей
противоположную сторону, называется высотой
треугольника.
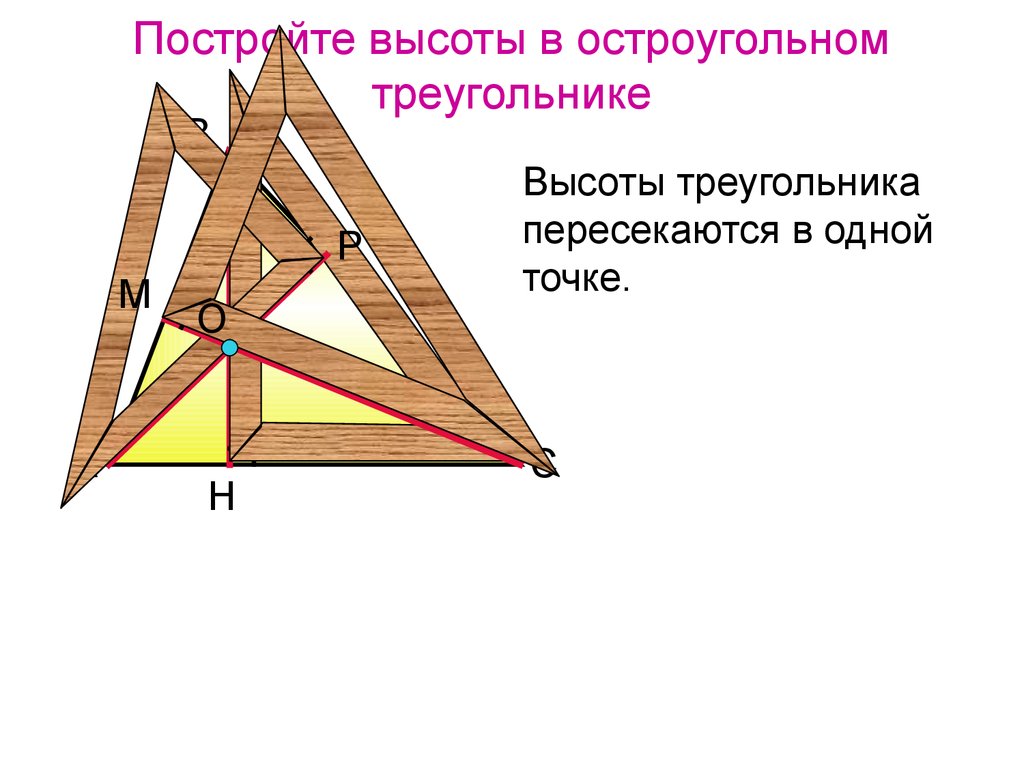
11. Постройте высоты в остроугольном треугольнике
ВР
М
А
О
Н
Высоты треугольника
пересекаются в одной
точке.
С
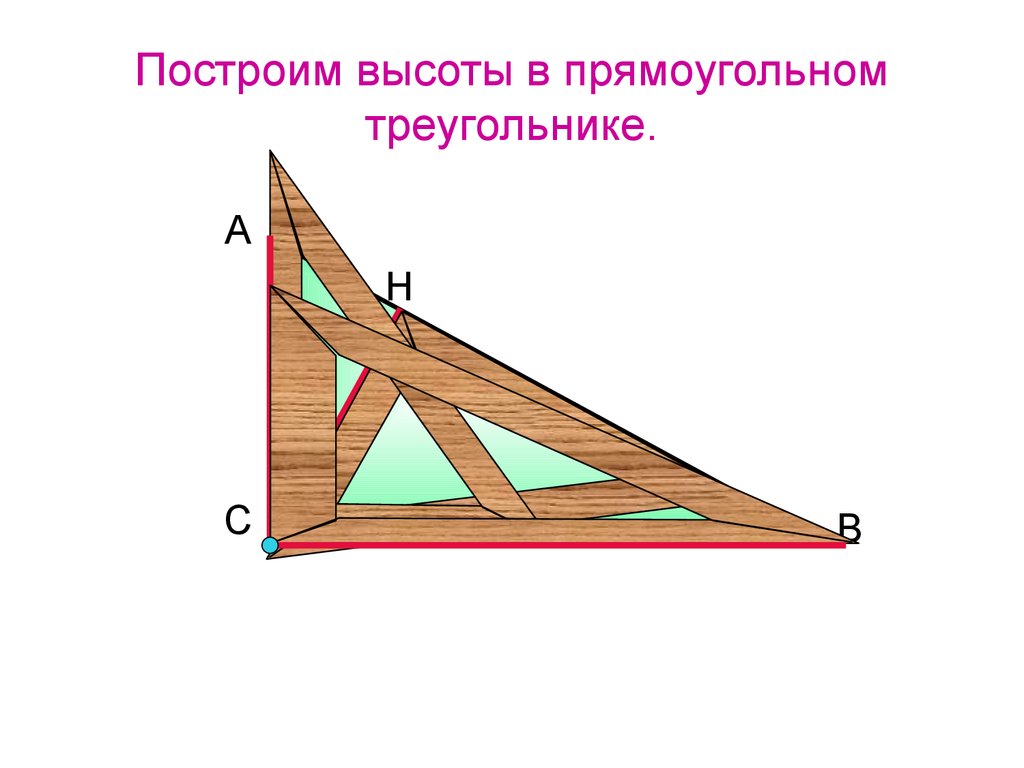
12. Построим высоты в прямоугольном треугольнике.
АН
С
В
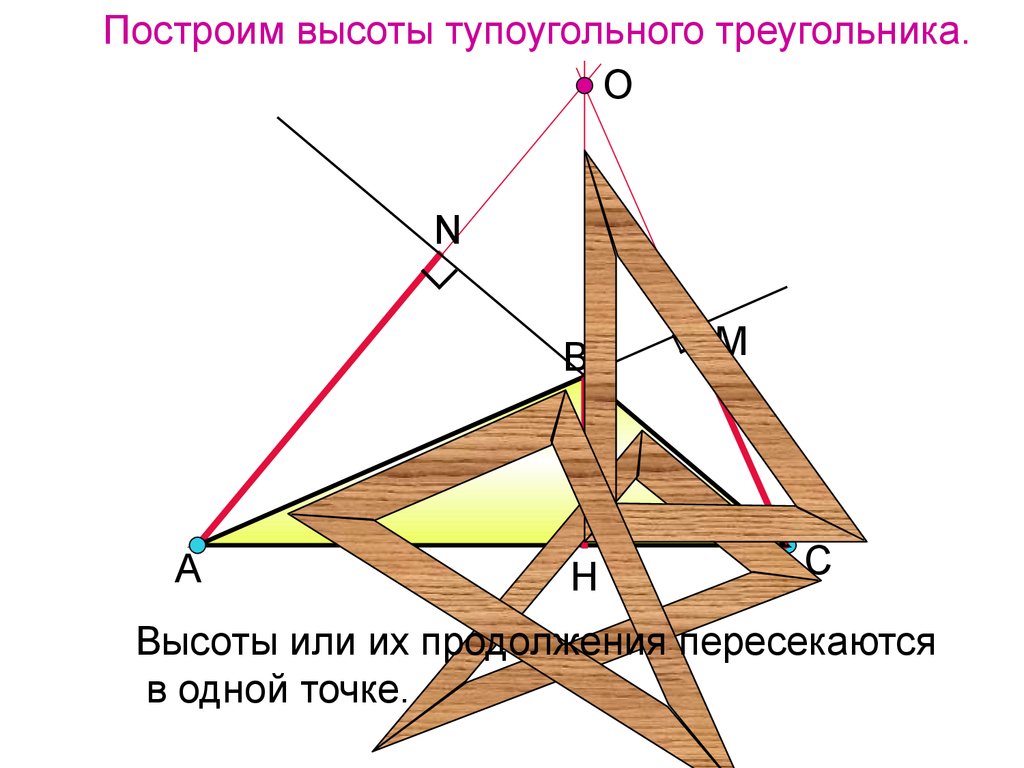
13. Построим высоты тупоугольного треугольника.
ОN
В
А
Н
М
С
Высоты или их продолжения пересекаются
в одной точке.
14.
Как называется отрезок АО?м
А
ед
н
а
и
а
О
Медиана
Медиана
биссектриса
биссектриса
А
В
Ы
С
О
Т
А
Медиана
Медиана
биссектриса
биссектриса
О
А
б
и
сс
ек
т
р
и
са
О
Медиана
Медиана
биссектриса
биссектриса
высота
высота
высота
высота
высота
высота
15.
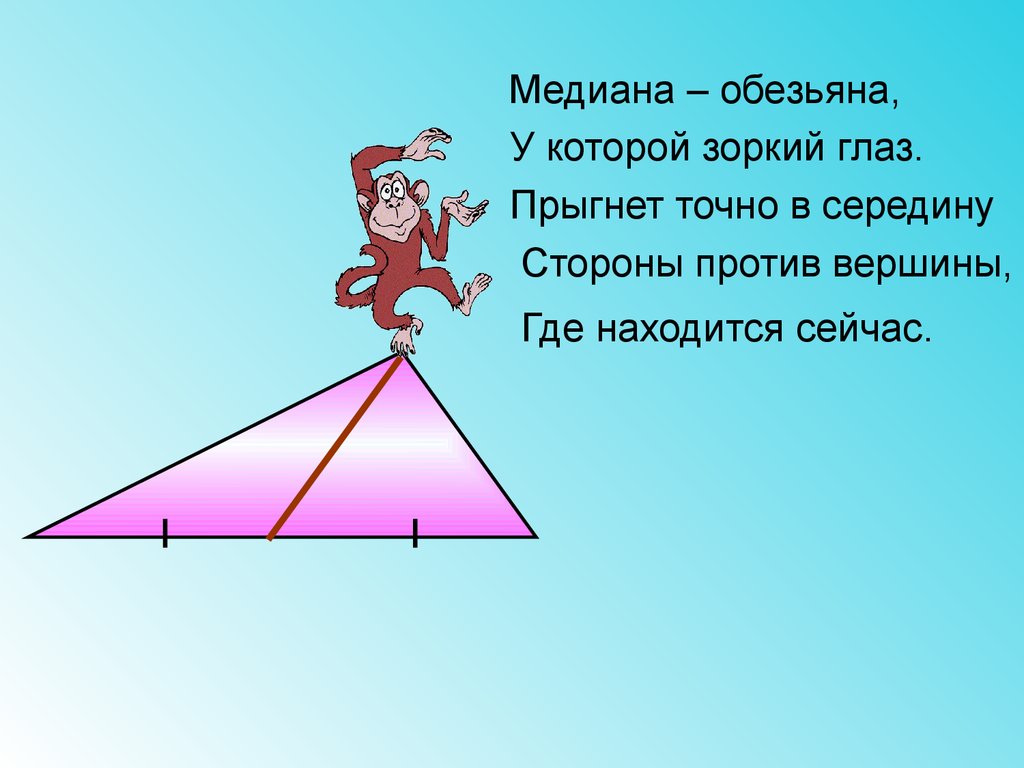
Медиана – обезьяна,У которой зоркий глаз.
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.
16.
Высота похожа на кота,Который выгнув спину
И под прямым углом
Соединит вершину
И сторону хвостом.
17. Домашнее задание:
§ 2. Пункты 16; 17Вопросы 5 – 9 стр. 47.
Практические задания
на отдельном листке формата А – 4. начертить высоты для остроугольного,
прямоугольного и тупоугольного треугольника
на отдельном листке формата А – 4. начертить биссектрисы для остроугольного,
прямоугольного и тупоугольного треугольника
на отдельном листке формата А – 4. начертить медианы для остроугольного, прямоугольного
и тупоугольного треугольника
сдать 3 листа, каждый лист подписать






 mathematics
mathematics








