дз (1)

1.

4.12 Классная работа
ТЕМА
Медиана,
биссектриса и
высота треугольника

2.

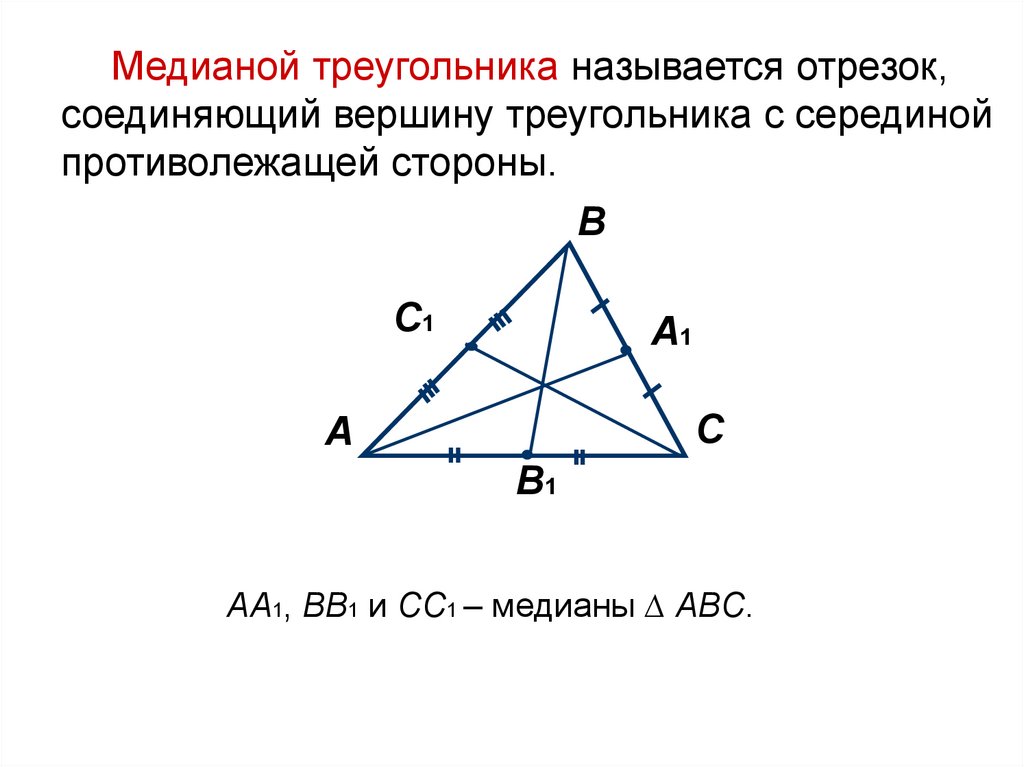
Медианой треугольника называется отрезок,
соединяющий вершину треугольника с серединой
противолежащей стороны.
В
C1
A1
С
А
B1
АA1, ВB1 и СC1 – медианы ∆ АВС.

3.

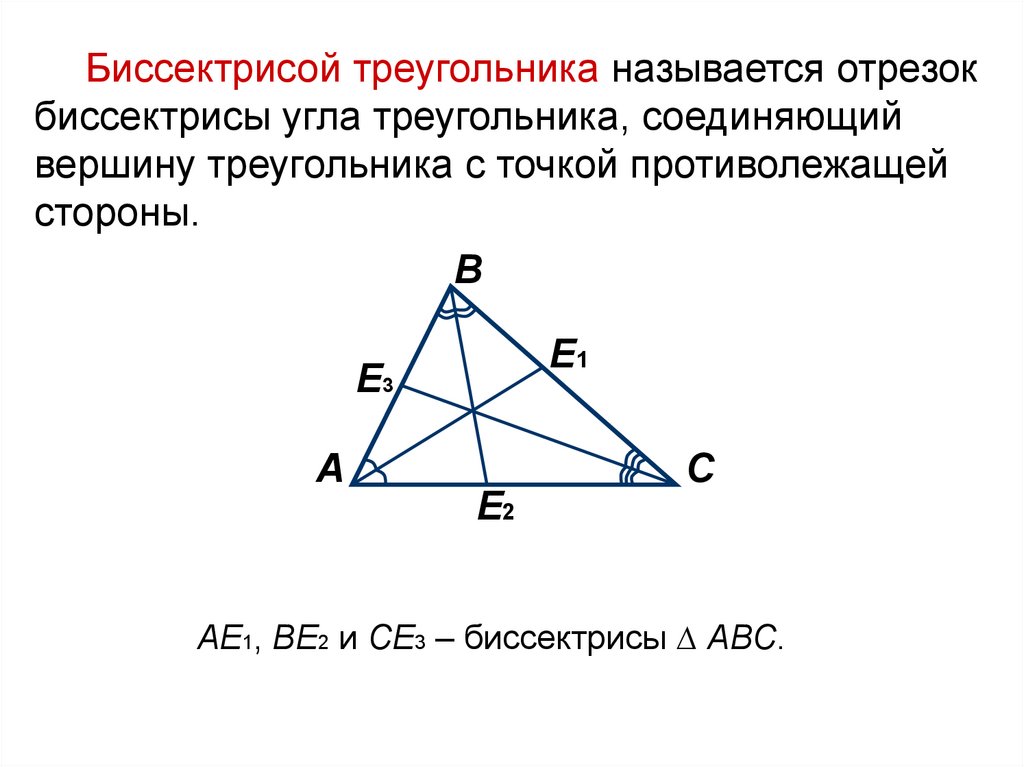
Биссектрисой треугольника называется отрезок
биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противолежащей
стороны.
B
E1
E3
А
C
E2
АE1, ВE2 и СE3 – биссектрисы ∆ АВС.

4.

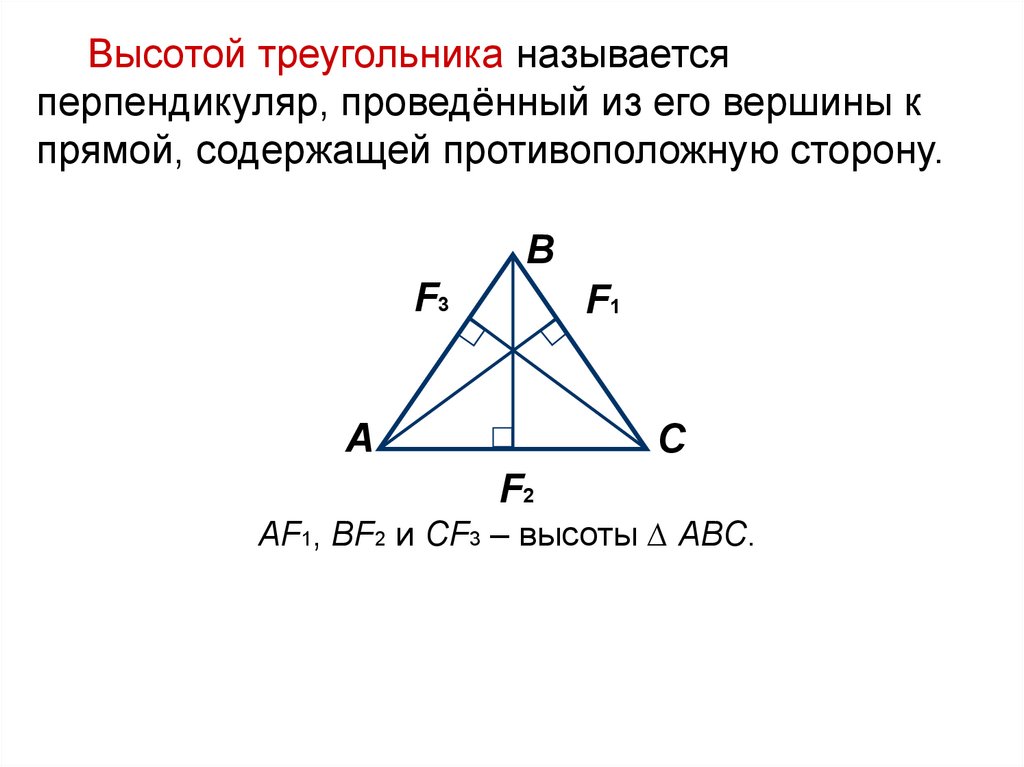
Высотой треугольника называется
перпендикуляр, проведённый из его вершины к
прямой, содержащей противоположную сторону.
В
F3
F1
А
С
F2
АF1, ВF2 и СF3 – высоты ∆ АВС.

5.

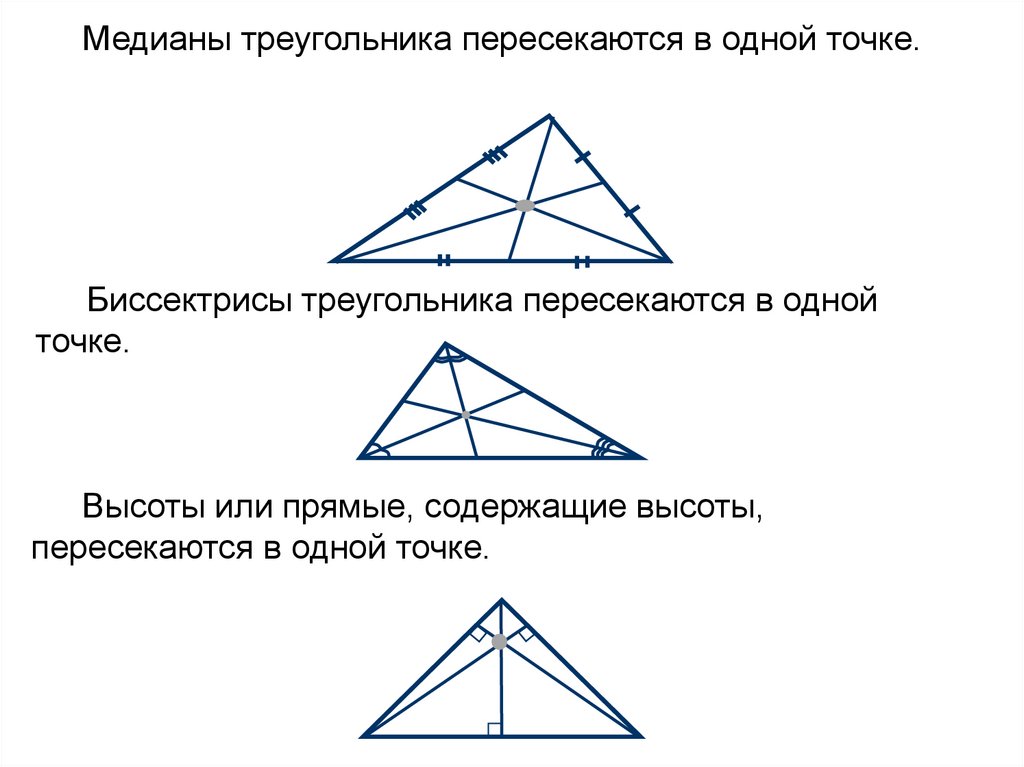
Медианы треугольника пересекаются в одной точке.
Биссектрисы треугольника пересекаются в одной
точке.
Высоты или прямые, содержащие высоты,
пересекаются в одной точке.

6.

Тест
А- 4
Б-2
В- 2
Г- 2
Д-2
А. Медианой треугольника называется …
1. линия, проходящая через вершину и середину противоположной стороны
треугольника
2. отрезок, соединяющий вершину с противоположной стороной треугольника
3. отрезок, соединяющий угол с серединой противоположной стороны треугольника
4. отрезок, соединяющий вершину треугольника с серединой противоположной
стороны
Б. Биссектрисой треугольника называется …
1. биссектриса, проведенная из вершины треугольника
2. отрезок биссектрисы угла треугольника, соединяющий вершину с точкой
противоположной стороны
3. прямая, проведенная из вершины треугольника как биссектриса угла
В. Высотой треугольника называется …
1. наибольшее расстояние между вершиной и противоположной стороной данного
треугольника
2. перпендикуляр из вершины к прямой, содержащей противоположную сторону
3. отрезок из вершины треугольника, перпендикулярный к противоположной стороне
Г. Все высоты треугольника пересекаются в двух точках
1. да
2. нет
3. не знаю
Д. Все медианы треугольника пересекаются в двух точках
1. да
2. нет
3. не знаю

7.

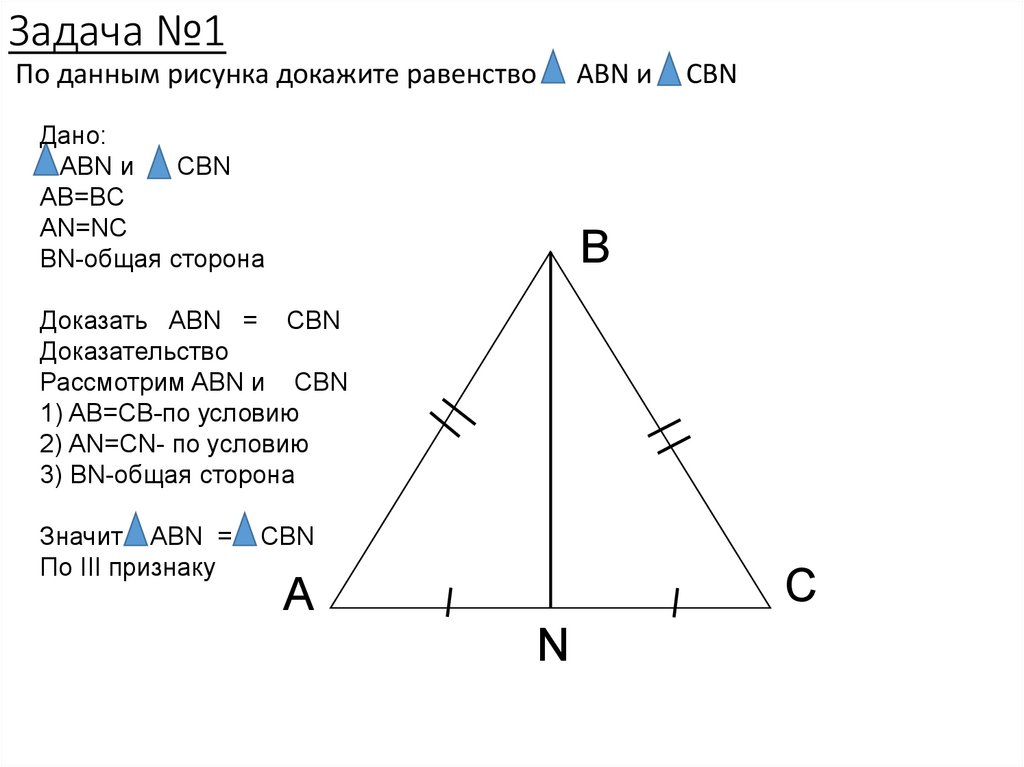
Задача №1
По данным рисунка докажите равенство
Дано:
ABN и
CBN
AB=BC
AN=NC
BN-общая сторона
ABN и
CBN
B
Доказать ABN = CBN
Доказательство
Рассмотрим ABN и CBN
1) AB=CB-по условию
2) AN=CN- по условию
3) BN-общая сторона
Значит ABN =
По III признаку
CBN
C
A
N

8.

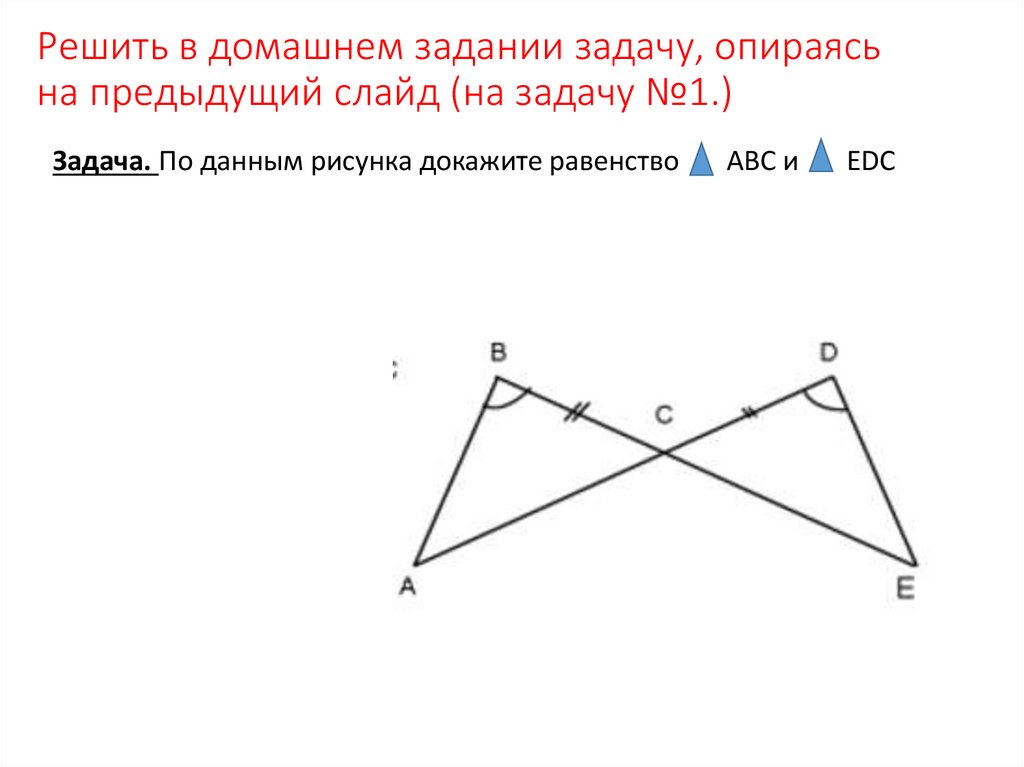
Решить в домашнем задании задачу, опираясь
на предыдущий слайд (на задачу №1.)
Задача. По данным рисунка докажите равенство
ABC и
EDC

9.

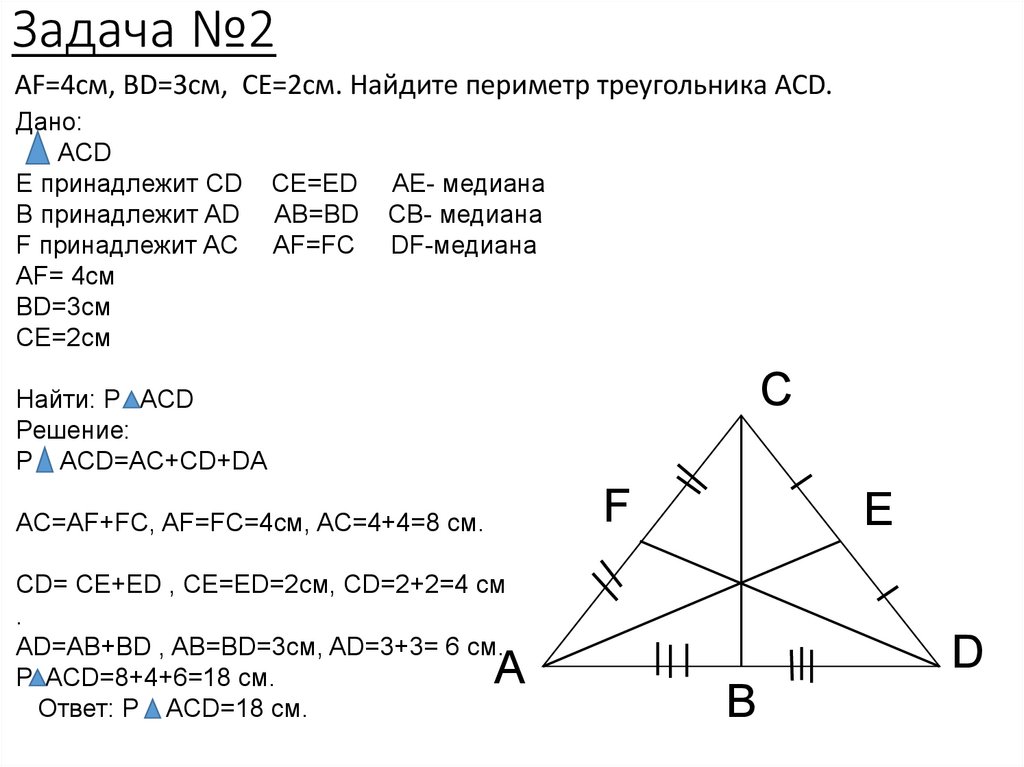
Задача №2
AF=4см, BD=3см, CE=2см. Найдите периметр треугольника ACD.
Дано:
ACD
Е принадлежит CD
B принадлежит AD
F принадлежит AC
AF= 4см
BD=3см
CE=2см
CE=ED
AB=BD
AF=FC
AE- медиана
СB- медиана
DF-медиана
C
Найти: P ACD
Решение:
P ACD=AC+CD+DA
F
AC=AF+FC, AF=FC=4см, AC=4+4=8 см.
CD= CE+ED , CE=ED=2см, CD=2+2=4 см
.
AD=AB+BD , AB=BD=3см, AD=3+3= 6 cм.
P ACD=8+4+6=18 см.
Ответ: P ACD=18 см.
A
E
D
B

10.

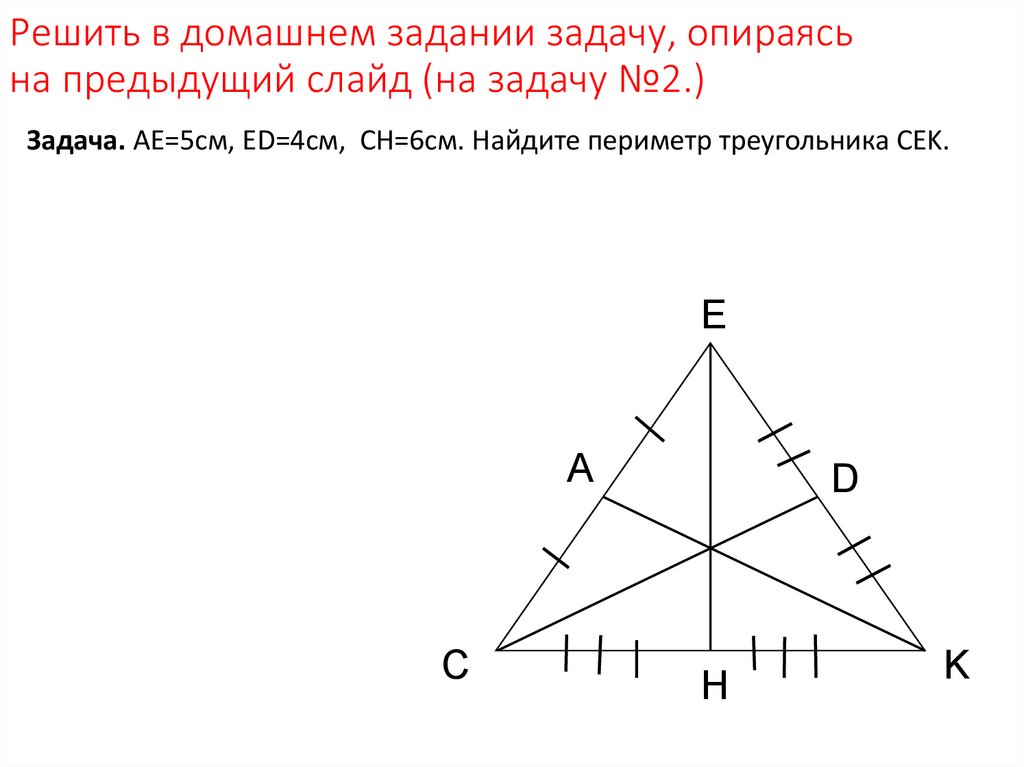
Решить в домашнем задании задачу, опираясь
на предыдущий слайд (на задачу №2.)
Задача. AE=5см, ED=4см, CH=6см. Найдите периметр треугольника CEK.
E
A
С
D
H
K

11.

Спасибо за урок.
До свидания!