Четность, нечетность, периодичность тригонометрических функций

1. Четность, нечетность, периодичность тригонометрических функций

Урок № 14
Четность, нечетность, периодичность
тригонометрических функций
План урока:
1 Четная и нечетная
функция
2 Периодическая
функция
3 Запись ДЗ
Я дама благородная,
Ведь функция я четная.
И у меня экстремумов не счесть.
Я не совсем обычная,
Ведь я периодическая,
И вот за это мне – хвала и честь.
О.Панишева

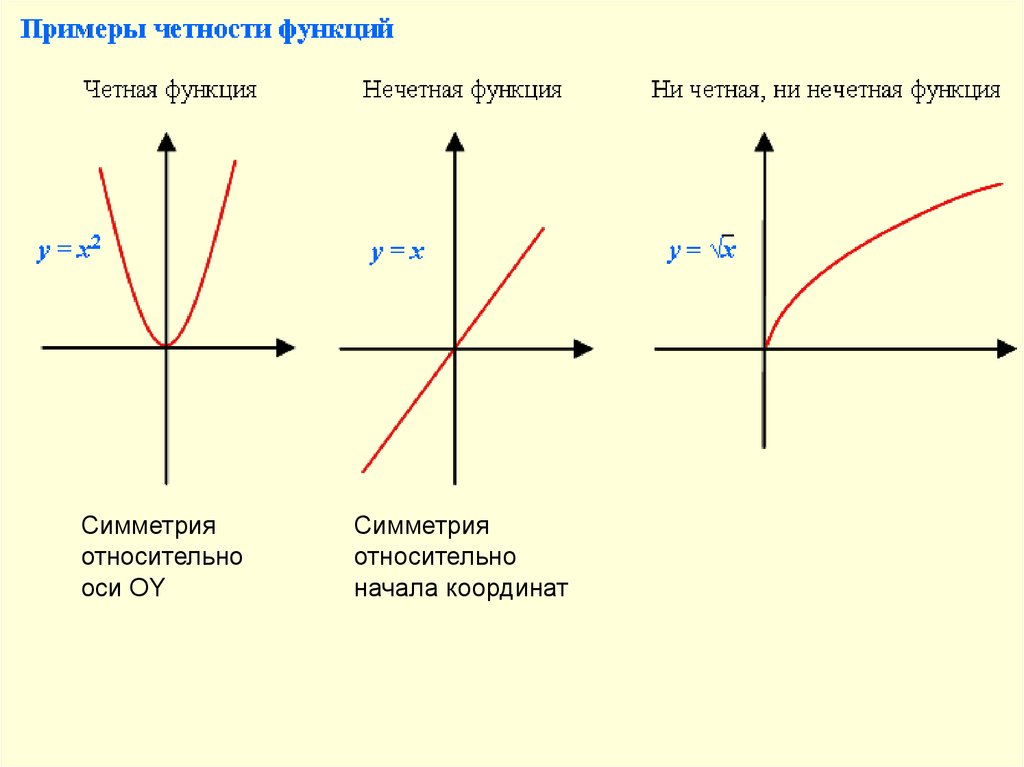
2.

Симметрия
относительно
оси OY
Симметрия
относительно
начала координат

3.

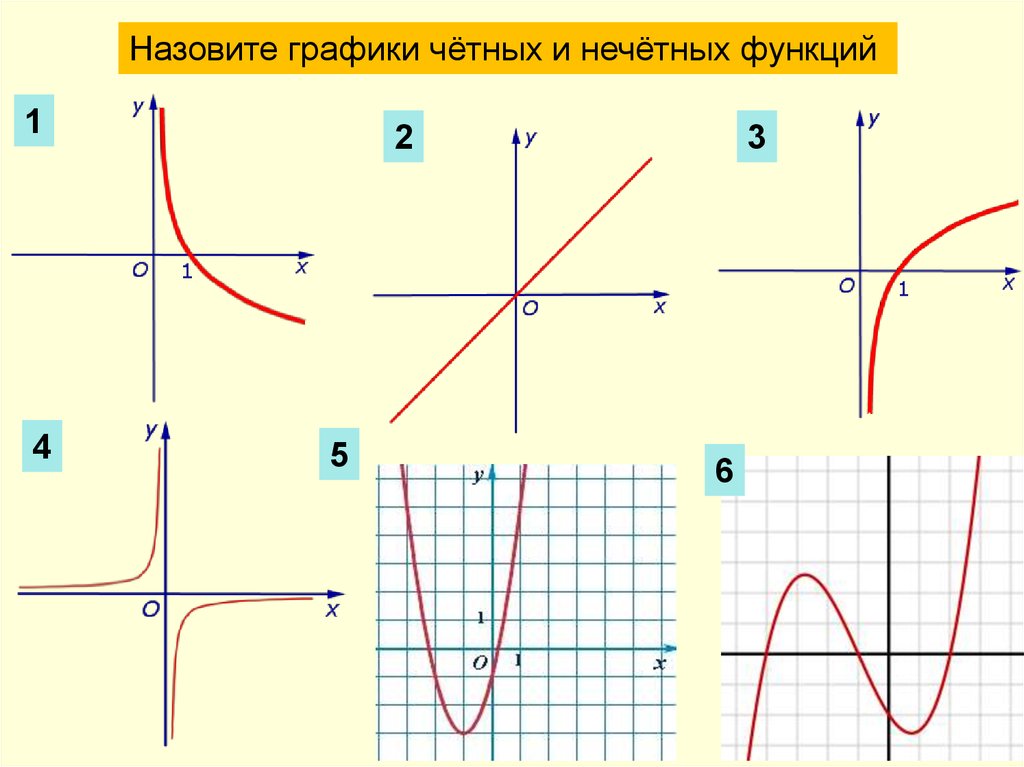
Назовите графики чётных и нечётных функций
1
4
2
5
3
6

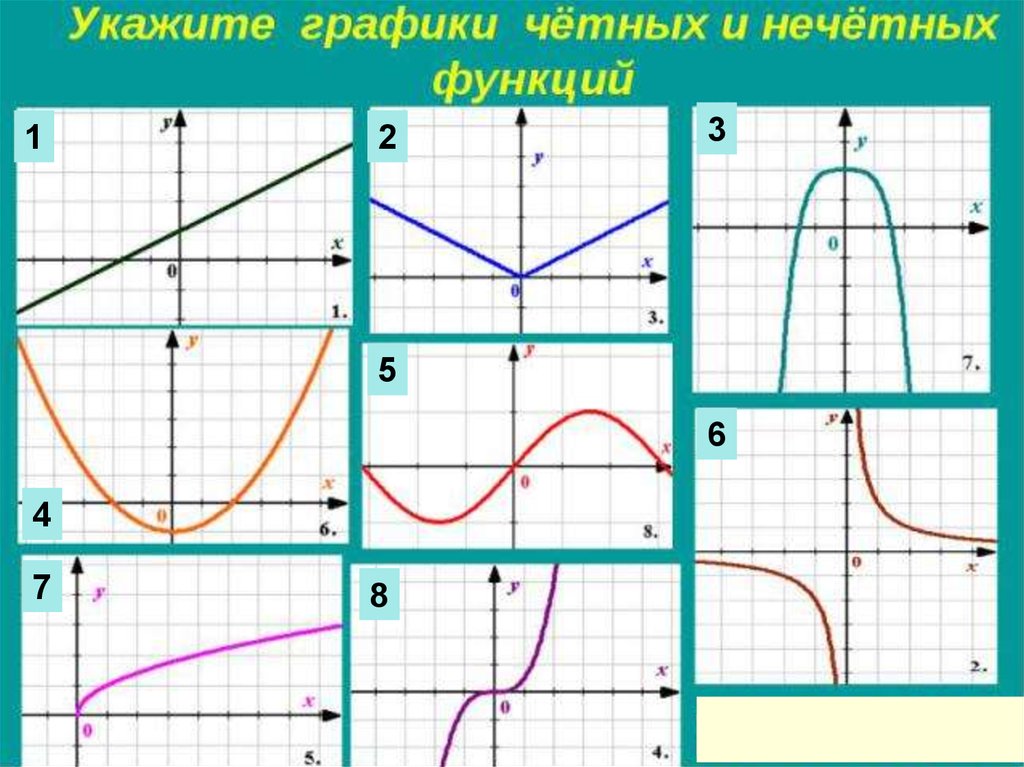
4.

1
2
3
5
6
4
7
8

5.

Четная и нечетная функция
Опр.
Функция называется чётной, если её
область определения симметрична относительно нуля
и для всех х выполняется равенство
f ( x) f ( x)
Опр.
Функция называется нечётной, если её
область определения симметрична относительно нуля
и для всех х выполняется равенство f ( x) f ( x)
Периодическая функция
Опр.
Функция называется периодической, если для всех х
из области определения функции выполняется
равенство
f ( x) f ( x Т ) f ( x T )
Т- некоторое число, называемое периодом функции.

6.

На уроке: №№ 700(1,3,5), 701(1)

7.

На уроке: №№ 702(1,3,5), 703(1,3)
Наименьший положительный период функции
y=sinx
y=cosx
T=2π
y=tgx
y=ctgx
T=π

8.

Наименьший положительный период
линейно зависимой функции
y=sin(kx+b)
y=cos(kx+b)
y=tg(kx+b)
y=ctg(kx+b)
T
Tʹ=│k│
Найдите наименьший положительный период функции
5x
y sin
4
x
y cos
7
9x
y tg
7
y сtg 5 х

9. Домашнее задание № 14

Учебник Алгебра 10-11 кл. Алимов
№№ 700(2,4,6), 701(2), 705